贝叶斯信念网络Bayes Belief network

贝叶斯信念网络Bayes Belief network

1. BBN

别称：贝叶斯网络、信念网络、概率网络

信念：相信专家给的概率

网络拓扑：

1. 数据构造
2. 专家构造
   可能不需要学习数据，整个网络可能都是由专家经验产生的

朴素贝叶斯：特征（属性）之间互相独立

但是特征之间不一定一定独立，会存在一些依赖。怎么解决？

联合条件概率分布

---

2. 两大成分

• 有向无环图

有向边：表示特征之间的关系
结点之间关系：

1. 独立（无关系）
2. 父结点、孩子结点：父结点是当前结点的因，孩子结点是当前结点的果

• 条件概率表CPT（Condition probability table）

表中的发生概率来自于专家

---

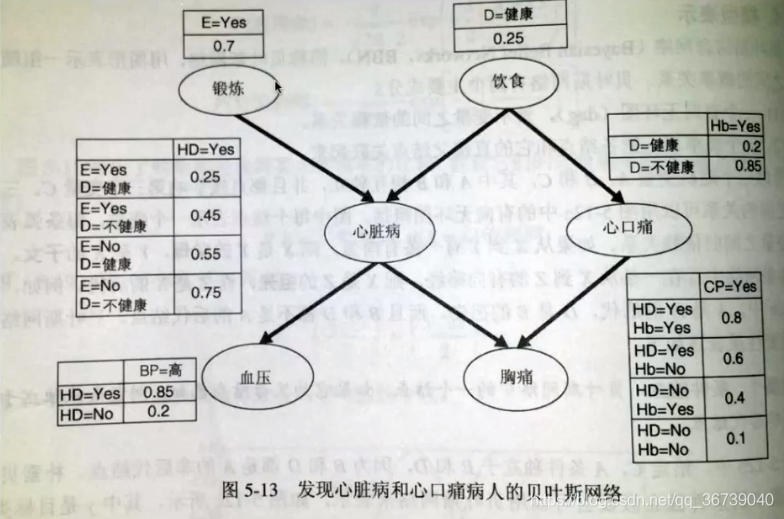
3. 先验概率

3.1.1 计算患心脏病的概率

$\alpha ：$ E的可能取值
$\beta ：$ D的可能取值
$P(E=\alpha ,D=\beta )=P(E=\alpha )P(D=\beta )：$E和D相互独立

3.1.2 计算血压高的概率

---

4. 条件概率

4.2.1 基于孩子结点，父母结点的条件概率

p(A|B)p(B) = p(AB)
p(B|A)p(A) = p(AB)

得出：
$$\frac{p(A|B)p(B)}{p(B|A)p(A)}=1$$
$$p(A|B)=\frac{p(B|A)p(A)}{p(B)}$$

4.2.2 基于父母结点，孩子结点的条件概率

4.2.3 结点之间独立

$$p(A|B)p(B)=p(AB)=p(A)p(B)$$
$$p(A|B)=p(A)$$

---

5. 网络拓扑

1. 网络拓扑未知
2. 网络拓扑已知，并且网络内部可观测
3. 网络拓扑已知，并且网络内部某些变量隐藏（缺失）

1：需要构造网络拓扑
3：需要训练网络，用以完整网络

5.1 未知网络拓扑

• 一些学习算法可通过训练数据来产生网络拓扑
• 专家构造

5.2 某些变量隐藏

有不同的方法来训练信念网络，比如梯度下降法（迭代的方式）Gradient descent。

梯度下降算法

目的：找出最大化该函数的权重的集合

1. 计算梯度

$$\frac{\partial ln{P}_w(D)}{\partial w_{ijk}}=\sum _{d=1}^{|D|}\frac{P(Y_i=y_{ij},U_i=u_{ik}|X_d)}{w_{ijk}}$$

D：数据集
$X_d$：训练元组，$X_d$的概率记为 p（可使用贝叶斯网路推理的标准算法求得）

2. 沿梯度方向前进一小步

$$w_{ijk}=w_{ijk}+l\frac{\partial ln{P}_w(D)}{\partial w_{ijk}}$$

$l$：表示步长的学习率（一般取小点，便于收敛）

3. 重新规格化权重

$w_{ijk}$是概率值，必须在[0,1]之间并且对于所有的i、k，${\sum }_j{w}_{ijk}必须等于1$。权重更新之后（第二步之后）可以对其规格化来保证上述条件

$w_{ijk}恒等于p(Y_i=y_{ij}|U_i=u_{ik})$
$w_{ijk}$：有双亲($U_i=u_{ik}$)的 变量($Y_i=y_{ij}$)的 CPT表目，可以看作权重，是对数据建模的重要参数
变量：网路中的结点

EM算法Expectation&Maximization

我们一直假设训练样本的所有的属性变量的值都已经被观测到（训练样本没有缺失），但是现实生活中往往会遇到“不完整”的训练样本（某个属性变量的值缺失）。存在这种“未观测（缺失）”的变量情况下，是否仍然能对模型参数进行估计呢？

未观测变量 = 隐变量 = 缺失变量

$$LL(\theta |X,Z)=lnP(X,Z|\theta )$$

X：已观测变量集合
Z：隐变量集合
$\theta$：模型参数

因为Z是隐变量，不可直接求得上式。
但是可以通过计算出Z的期望，之后最大化已观测数据的对数似然（在这儿叫：边际似然）
$$LL(\theta |X)=lnP(X|\theta )=ln\sum _{Z}P(X,Z|\theta )$$
$$公式7.35$$

EM算法是常用的估计参数隐变量的利器，它是一种迭代式的方法，基本思想是：
若参数$\theta$已知，则可根据训练数据推断出最优隐变量Z的值；
反之，若Z的值已知，则可方便地对参数$\theta$做极大似然估计。

依照基本思想，我们可以给一个${\theta }_0$初始值，然后对公式7.35进行迭代：
EM原型：

1. 给一个${\theta }_0$初始值
2. 基于${\theta }^t$推断隐变量Z的期望，记为$Z^t$;
3. 基于X(已观测变量)和 $Z^t$ 对 $\theta$ 进行极大似然估计，获得 ${\theta }^{t+1}$。
4. 重复2、3，直到获得局部最优解。

若不是取Z的期望，而是基于${\theta }^t$计算隐变量Z的概率分布$P(Z|X,{\theta }^t)$，EM的两个步骤：

• E：基于${\theta }^t$推断隐变量分布$P(Z|X,{\theta }^t)$，并且计算对数似然$LL(\theta |X,Z)$关于Z的期望。
• M：寻找参数最大化期望似然，即：$${\theta }^{t+1}=argma{x}_{\theta }Q(\theta |{\theta }^t)$$