树链剖分

链可以看做是一种特殊的树，当一棵树退化成了链，某些问题就变得容易解决，也有很多数据结构支持这样那样的操作，线段树就是其中一种。从而我们可以想象，能否把一棵树也分成很多条链，从而来解决一些问题呢？这就有了树链剖分。

形象点说，树链剖分就是把一棵树分成多条链（称为“重链”），链与链之间有一些边相连，当操作在链上时，可以用线段树来维护，但在链与链之间的边（称为“轻边”，也叫“轻链”）就需要直接维护。在重链上，维护的时间复杂度为log级别的，而轻链需要一个个维护，如此看来，树链剖分的时间复杂度与轻链的条数有着直接的关系。那么就有一个问题，如何剖分才能够使轻链尽可能的少？

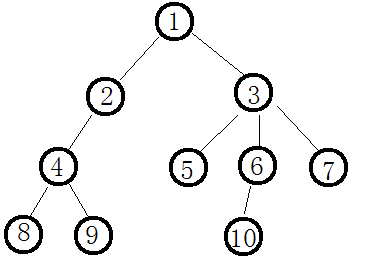
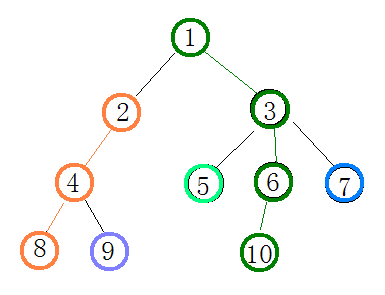
树链剖分是这样解决这个问题的：首先，每个点都必须在重链上（一条重链可以只有一个点），那么就需要把其中的一些重链加入一些点，使得重链的条数减少。对于一棵树，从下往上处理（即先处理深度比较大的）。size（i）记为以结点i为根的子树的结点数，某个点的重儿子就是指该结点儿子中size值最大的一个，其余的儿子称为“轻儿子”（也可能没有儿子）。每个结点加入它重儿子所在的重链。如图：点1的重儿子是点3，点3的重儿子为点6，点4的重儿子为点8或点9（若size值相等，则任选一个作为重儿子，下面的例子是取点8）。

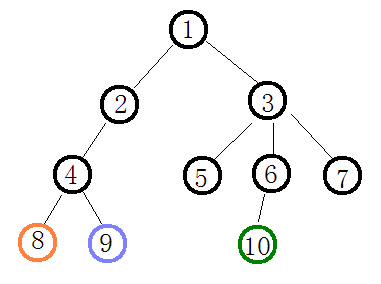
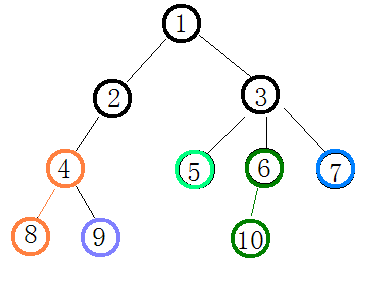
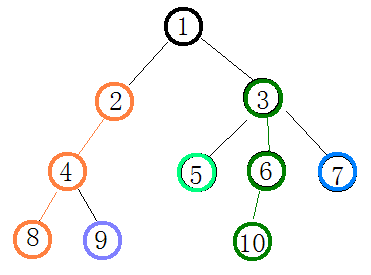
我们按深度处理，除黑色代表未处理的点，不同的颜色为不同的重链：

如样例，就有五条重链，四条轻链（黑色的边）。现在需要证明的是，按照如此剖分的方法，从任意一点到根结点经过的轻链不超过log n条。假设是从点i出发。若i向上走一步，经过了一条轻链，来到了它的父亲k（如图点5走一步到点3），size（k）必然大于size（i）* 2 ，因为点i不是点k的重儿子，点k必然有一个重儿子j，使得size（j）≥size（i），那么自然有size（k）＞size（i）* 2 。也就是说，每经过一条轻链，size（i）就要翻一倍，所以最坏情况下只会翻倍log n次，如果超过了log n，那么这棵树的结点就要超过n啦，是不符题意的。

如此看来，从任意一点到另一点，经过的轻链不会超过2 * log n。时间复杂度就得到了保障，加上重链的维护，那就是O（2 * log n + 2 * log n * log n），这是最坏情况，一般很难达到。

下面再说说具体实现的步骤，是对于点的修改和询问。若是基于边的修改和查询，那么把每条边的权值附在它下面的那个点上（如样例，连接点3和点6的那条边的值就保存在点6上），这样能够保证每条边都有可依附的点。

有一种写法是把所有的点都放进一棵线段树，这样代码是短，但我觉得比较慢。起码比下面的方法慢3倍。

我写的是多棵线段树，用指针实现。剖分的过程用宽搜。

npaht：重链条数。

top（i）：重链i最顶端结点。

len（i）：重链i的长度。

belong（i）：结点i属于哪条重链。

idx（i）：结点i所在的重链的编号。如样例，绿色重链中，idx(10) = 0, idx(6) = 1, idx(3) = 2, idx(1) = 3。

dep（i）：结点i的深度。

size（i）：以结点i为根的子树的结点个数。

father （i）：结点i的父亲。

还有，对于两点操作，并不需要找它们的最近公共祖先，只需要看它们所在重链的顶端结点的深度，深度低的往上跳，直到两点在同一重链。

#include <cstdio>
#include <algorithm>
using namespace std;

// 读入优化
inline int getInt()
{
	int res = 0;
	char ch;
	for (ch = '#'; ch < '0' || ch > '9'; ch = getchar());
	for (; ch >= '0' && ch <= '9'; ch = getchar()) 
		res = res * 10 + (int) ch - (int) '0';
	return res;
}

// 得到题目的操作
inline char getCommend()
{
	char ch, t;
	for (ch = ' '; ch == ' ' || ch == '\n'; ch = getchar());
	t = ch;
	for (; ch != ' ' && ch != '\n'; ch = getchar());
	return t;
}

const int inf = 1000007;		// 无穷大
const int N = 10007;			// 最多的结点个数

int n, edgeval[N];				// 每条边的初始值
// 数组模拟指针，from为头，to为连接的点，next为下一个。nedge为边数
int from[N], to[N << 1], next[N << 1], nedge;
// 每条边依附的点
int edgepos[N];

// 插入边
void Insert(int a, int b)
{
	to[nedge] = b;
	next[nedge] = from[a];
	from[a] = nedge ++;
}

// 读入
void Init()
{
	memset(from, -1, sizeof(from));
	nedge = 0;
	n = getInt();
	for (int i = 0; i + 1 < n; i ++) 
	{
		int a = getInt() - 1, b = getInt() - 1;
		edgeval[i] = getInt();
		Insert(a, b);
		Insert(b, a);
	}
}

int top[N], len[N], npath;
int belong[N], idx[N], dep[N], size[N], father[N], Q[N];

void Split()
{
	npath = 0;
	int lo = 0, hi = 0;
	Q[0] = 0;
	dep[0] = 0;
	father[0] = -1;
	
	while (lo <= hi)
	{
		int u = Q[lo ++];
		for (int e = from[u]; e != -1; e = next[e])
		{
			int v = to[e];
			if (v != father[u])
			{
				edgepos[e >> 1] = v;
				Q[++ hi] = v;
				dep[v] = dep[u] + 1;
				father[v] = u;
			}
		}
	}
	
	for (int i = n - 1; i >= 0; i --)
	{
		// p为重儿子的编号
		int u = Q[i], p = -1;
		size[u] = 1;
		for (int e = from[u]; e != -1; e = next[e])
		{
			int v = to[e];
			if (v != father[u])
			{
				size[u] += size[v];
				if (p == -1 || size[v] > size[p]) // 求重儿子
					p = v;
			}
		}
		
		if (p == -1)
		{
			belong[u] = npath;
			len[npath] = 1;
			idx[u] = 0;
			top[npath ++] = u;
		}
		else 
		{
			int x = belong[p];
			belong[u] = x;
			idx[u] = len[x] ++;
			top[x] = u;
		}
	}
}

int nnode;
// 线段树的结点
struct Node
{
	Node *lch, *rch;
	int lo, hi, dat;
	inline int mi()
	{
		return (lo + hi) >> 1;
	}
}node[N << 1], *tree[N];

void Build(Node *p, int lo, int hi)
{
	p -> lo = lo;
	p -> hi = hi;
	p -> dat = - inf;
	if (lo + 1 < hi)
	{
		int mi = p -> mi();	
		p -> lch = &node[nnode ++];
		p -> rch = &node[nnode ++];
		Build(p -> lch, lo, mi);
		Build(p -> rch, mi, hi);
	}
}

void Modify(Node *p, int pos, int val)
{
	if (p -> lo + 1 == p -> hi) 
		p -> dat = val;
	else 
	{
		int mi = p -> mi();
		if (pos < mi) Modify(p -> lch, pos, val);
		else Modify(p -> rch, pos, val);
		p -> dat = max(p -> lch -> dat, p -> rch -> dat);
	}
}

int Ask(Node *p, int le, int ri)
{
	if (le <= p -> lo && ri >= p -> hi) 
		return p -> dat;
	else 
	{
		int mi = p -> mi();
		int ret = - inf;
		if (le < mi) ret = max(ret, Ask(p -> lch, le, ri));
		if (ri > mi) ret = max(ret, Ask(p -> rch, le, ri));
		return ret;
	}
}

void Prepare()
{
	nnode = 0;
	for (int i = 0; i < npath; i ++)
	{
		tree[i] = &node[nnode ++];
		Build(tree[i], 0, len[i]);
	}
	// 初始化边的权值
	for (int i = 0; i + 1 < n; i ++)
	{
		int u = edgepos[i];
		Modify(tree[belong[u]], idx[u], edgeval[i]);
	}
}

// 对于两点操作
int Find(int a, int b)
{
	int res = - inf;
	// x是点a所在的重链，y是点b所在的重链
	int x = belong[a], y = belong[b];
	
	while (x != y)
	{
		// 选择顶端元素深度较深的往上跳
		if (dep[top[x]] < dep[top[y]])
		{
			swap(a, b);
			swap(x, y);
		}
		res = max(res, Ask(tree[x], idx[a], len[x]));
		// 跳的过程
		a = father[top[x]];
		x = belong[a];
	}
	// 直到在同一重链
	if (idx[a] != idx[b])
	{
		if (idx[a] > idx[b]) swap(a, b);
		res = max(res, Ask(tree[x], idx[a], idx[b]));
	}
	return res;
}

void Solve()
{
	while (true)
	{
		char commend = getCommend();
		switch (commend) 
		{
			case 'C':
				int e = getInt() - 1, v = getInt();
				int u = edgepos[e];
				Modify(tree[belong[u]], idx[u], v);
				break;
			case 'Q':
				int a = getInt() - 1, b = getInt() - 1;
				printf("%d\n", Find(a, b));
				break;
			case 'D':
				return;
				break;
		}
	}
}

int main()
{
	for (int T = getInt(); T; T --)
	{
		Init();
		Split();
		Prepare();
		Solve();
	}
	
	return 0;
}