字符串匹配的几种算法总结（KMP、等）

字符串匹配（string match)是在实际工程中经常会碰到的问题，通常其输入是原字符串(String)和子串（又称模式，Pattern)组成，输出为子串在原字符串中的首次出现的位置。通常精确的字符串搜索算法包括暴力搜索(Brute force)，KMP, BM(Boyer Moore), sunday, robin-karp 以及 bitap。下面分析这几种方法并给出其实现。假设原字符串长度M，字串长度为N。

1. Brute force.

该方法又称暴力搜索，也是最容易想到的方法。

预处理时间 O(0)

匹配时间复杂度O(N*M)

主要过程：从原字符串开始搜索，若出现不能匹配，则从原搜索位置+1继续。

[cpp]  view plain copy

1. /*  
2.  * ===  FUNCTION  ====================================================================== 
3.  *         Name:  bf 
4.  *  Description: brute-force method for string match problem. 
5.  * ===================================================================================== 
6.  */  
7. int bf(const char *text, const char *find)  
8. {  
9.     if (text == '/0' || find == '/0')  
10.         return -1;  
11.     int find_len = strlen(find);  
12.     int text_len = strlen(text);  
13.     if (text_len < find_len)  
14.         return -1;  
15.     char *s = text;  
16.     char *p = s;  
17.     char *q = find;  
18.     while (*p != '/0')  
19.     {  
20.         if (*p == *q)  
21.         {  
22.             p++;  
23.             q++;  
24.         }  
25.         else  
26.         {  
27.             s++;  
28.             p = s;  
29.             q = find;  
30.         }  
31.         if (*q == '/0')  
32.         {  
33.             return (p - text) - (q - find);  
34.         }  
35.     }  
36.     return -1;  
37. }  

 

 

2，KMP.

KMP是经典的字符串匹配算法。

预处理时间：O(M)

匹配时间复杂度：O(N)

主要过程：通过对字串进行预处理，当发现不能匹配时，可以不进行回溯。

[cpp]  view plain copy

1. /*  
2.  * ===  FUNCTION  ====================================================================== 
3.  *         Name:  kmp 
4.  *  Description:  kmp method for string match. 
5.  * ===================================================================================== 
6.  */  
7. /* 
8.  * examples of prepocessing for pattern 
9.  * pattern_1:  
10.  * a b c a b c a 
11.  * 0 0 0 0 1 2 3 
12.  * pattern_2: 
13.  * a a a a b a a 
14.  * 0 0 0 0 0 0 1 
15.  */  
16. int kmp(const char *text, const char *find)  
17. {  
18.     if (text == '/0' || find == '/0')  
19.         return -1;  
20.     int find_len = strlen(find);  
21.     int text_len = strlen(text);  
22.     if (text_len < find_len)  
23.         return -1;  
24.     int map[find_len];  
25.     memset(map, 0, find_len*sizeof(int));  
26.     //initial the kmp base array: map  
27.     map[0] = 0;  
28.     map[1] = 0;  
29.     int i = 2;  
30.     int j = 0;  
31.     for (i=2; i<find_len; i++)  
32.     {  
33.         while (1)  
34.         {  
35.             if (find[i-1] == find[j])  
36.             {  
37.                 j++;  
38.                 if (find[i] == find[j])  
39.                 {  
40.                     map[i] = map[j];  
41.                 }  
42.                 else  
43.                 {  
44.                     map[i] = j;  
45.                 }  
46.                 break;  
47.             }  
48.             else  
49.             {  
50.                 if (j == 0)  
51.                 {  
52.                     map[i] = 0;  
53.                     break;  
54.                 }  
55.                 j = map[j];  
56.             }  
57.         }  
58.     }  
59.     i = 0;  
60.     j = 0;  
61.     for (i=0; i<text_len;)  
62.     {  
63.         if (text[i] == find[j])  
64.         {  
65.             i++;  
66.             j++;  
67.         }  
68.         else  
69.         {  
70.             j = map[j];  
71.             if (j == 0)  
72.                 i++;  
73.         }  
74.         if (j == (find_len))  
75.             return i-j;  
76.     }  
77.     return -1;  
78. }  

 

注意：在预处理中，表面看起来时间复杂度为O(N^2)，但是为什么是线性的，在时间复杂度分析中中，通过观察变量的变化来统计零碎的、执行次数不规则的情况，这种方法叫做摊还分析。我们从上述程序的j 值入手。每一次执行上述循环预处理语句中的第二个else时都会使j减小（但不能减成负的），而另外的改变j值的地方只有一处。每次执行了这一处，j都只能加1；因此，整个过程中j最多加了M-1个1。于是，j最多只有M-1次减小的机会（j值减小的次数当然不能超过M-1，因为j永远是非负整数）。这告诉我们，while循环总共最多执行了M-1次。按照摊还分析的说法，平摊到每次for循环中后，一次for循环的复杂度为O(1)。整个过程显然是O(M)的。另外关于KMP的详细分析，可以参考Matrix67KMP算法详解。

 

3，Boyer Moore

Boyer Moore是字符串匹配算法中的经典，可以参考论文a faster string searching algorithm。

预处理时间O(N + M^2)

匹配时间复杂度O(N)

主要过程：通过预处理原字符串以及待匹配字串，从而在匹配失败时可以跳过更多的字符。

[cpp]  view plain copy

1. /*  
2.  * ===  FUNCTION  ====================================================================== 
3.  *         Name:  bm 
4.  *         Descritexttion:  Boyer–Moore method for string match. 
5.  *====================================================================================== 
6.  */  
7. int bm(const char *text, const char *find)  
8. {  
9.     if (text == '/0' || find == '/0')  
10.         return -1;  
11.     int i, j, k;  
12.     int text_len = strlen(text);  
13.     int find_len = strlen(find);  
14.     if (text_len < find_len)  
15.         return -1;  
16.     int delta_1[CHAR_MAX];  
17.     for (i=0; i<CHAR_MAX; i++)  
18.         delta_1[i] = find_len;  
19.     for (i=0; i<find_len; i++)  
20.         delta_1[find[i]] = find_len - i - 1;  
21.     int rpr[find_len];  
22.     rpr[find_len-1] = find_len - 1;  
23.     for (i=find_len-2; i>=0; i--)  
24.     {  
25.         int len = (find_len - 1) - i;  
26.         //find the reoccurence of the right most (len) chars  
27.         for (j=find_len-2; j>=(len-1); j--)  
28.         {  
29.             if (strncmp(find+i+1, find+j-len+1, len) == 0)  
30.             {  
31.                 if ((j-len) == -1 || find[i] != find[j-len])  
32.                 {  
33.                     rpr[i] = j - len + 1;  
34.                     break;  
35.                 }  
36.             }  
37.         }  
38.         //if the right most (len) chars not completely occur, we find the right  
39.         //substring of (len). every step, we try to find the right most (len-k)  
40.         //chars.  
41.         for (k=1; j<(len-1) && k<len; k++)  
42.         {  
43.             if (strncmp(find+i+k, find, len-k) == 0)  
44.             {  
45.                 rpr[i] = 0 - k;  
46.                 break;  
47.             }  
48.         }  
49.         if (j<(len-1) && k == len)  
50.         {  
51.             rpr[i] = 0 - len;  
52.         }  
53.     }  
54.     int delta_2[find_len];  
55.     for (i=0; i<find_len; i++)  
56.         delta_2[i] = find_len - rpr[i];  
57.     i = find_len - 1;  
58.     j = find_len - 1;  
59.     while (i < text_len)  
60.     {  
61.         if (text[i] == find[j])  
62.         {  
63.             i--;  
64.             j--;  
65.         }  
66.         else  
67.         {  
68.             if (delta_1[text[i]] > delta_2[j])  
69.             {  
70.                 i += delta_1[text[i]];  
71.             }  
72.             else  
73.             {  
74.                 i += delta_2[j];  
75.             }  
76.             j = find_len - 1;  
77.         }  
78.         if (j == -1)  
79.             return i+1;  
80.     }  
81.       
82.     return -1;  
83. }  

 

提示：该算法主要利用坏字符规则和好后缀规则进行转换。所谓坏字符规则，是指不能匹配时的字符在待匹配字串中从右边数的位置；而好后缀规则则是指子串中从该不匹配位置后面所有字符（都是已匹配字符）再次在字串中出现的位置(k)，其中s[k,k+1,---,k+len-j-1] = s[j+1, j+1,---,len-1], 并且s[k-1] !=  [j] || s[k-1] = $, 其中$表示增补的字符，可以与任何字符相等。

举例来说，对于字串ABCXXXABC

   -4  -3 -2 -10  1 23  4 56  7 89

A BC  X XX  A BC

j=9 9//NULL->其值为当前位置。

j=8 $0      //C->虽然出现在3，但[2] = [j]，所以不满足

j=7 $$ -1   //BC出现在开始[2]，但[1]=[j]

j=6 1   //ABC

j=5 $0     //XABC

j=4 $$ -1   //XXABC

j=3 $$  $ -2 //XXXABC

j=2 $  $ $$  -3  //CXXXABC

j=1 $  $ $$  $ -4  //BCXXXABC

 

4, Sunday

Sunday算法比较简单，其实就是利用Boyer Moore中的坏字符规则，实现起来简单，效果也还不错。

预处理时间O(M)

匹配时间复杂度O(N*M)

[cpp]  view plain copy

1. /*  
2.  * ===  FUNCTION  ====================================================================== 
3.  *         Name:  sunday 
4.  *  Description:  sunday method for string match. 
5.  * ===================================================================================== 
6.  */  
7. int sunday(const char *text, const char *find)  
8. {  
9.     if (text == '/0' || find == '/0')  
10.         return -1;  
11.     char map[CHAR_MAX];  
12.     int i;  
13.     int text_len = strlen(text);  
14.     int find_len = strlen(find);  
15.     if (text_len < find_len)  
16.         return -1;  
17.     //preprocess  
18.     for (i=0; i<CHAR_MAX; i++)  
19.         map[i] = find_len + 1;  
20.     for (i=0; i<find_len; i++)  
21.         map[find[i]] = find_len - i;  
22.     //match process  
23.     i = 0;  
24.     while (i <= (text_len - find_len))  
25.     {  
26.         if (strncmp(find, text + i, find_len) == 0)  
27.             return i;  
28.         else  
29.             i += map[text[i + find_len]];  
30.     }  
31.     return -1;  
32. }  

 

 

5, Robin-Karp

Robin-Karp主要利用HASH函数来处理字串，从而完成匹配。

预处理时间O(0)

最坏匹配时间复杂度O(N*M)

[cpp]  view plain copy

1. /*  
2.  * ===  FUNCTION  ====================================================================== 
3.  *         Name:  robin_karp 
4.  *  Description:  robin_karp method for string match problem. 
5.  * ===================================================================================== 
6.  */  
7. // karp_robin need a hash function  
8. int hash(const char *s, unsigned int len)  
9. {  
10.     int result = 0;  
11.     int base = 3;  
12.     int i;  
13.       
14.     for (i=0; i<len; i++)  
15.     {  
16.         result += s[i];  
17.         result *= base;  
18.     }  
19.     result /= base;  
20.     return result;  
21. }  
22. int robin_karp(const char *text, const char *find)  
23. {  
24.     if (text == '/0' || find == '/0')  
25.         return -1;  
26.     int i, j;  
27.     int text_len = strlen(text);  
28.     int find_len = strlen(find);  
29.     if (text_len < find_len)  
30.         return -1;  
31.     int h_find = hash(find, find_len);  
32.     int h_tmp = 0;  
33.     for (i=0; i<=(text_len-find_len); i++)  
34.     {  
35.         h_tmp = hash(text+i, find_len);  
36.         if (h_tmp == h_find)  
37.         {  
38.             for (j=0; j<find_len; j++)  
39.             {  
40.                 if (find[j] != text[i+j])  
41.                 {  
42.                     break;  
43.                 }  
44.             }  
45.             if (j == find_len)  
46.                 return i;  
47.         }  
48.     }  
49.     return -1;  
50. }  

 

注意：主要依赖于hash函数的设计。

 

6, Bitap

Bitap算法主要利用位运算进行字符串的匹配，其匹配过程可以看作是有穷自动机中状态的转换，按照字串(pattern)的连续分解状态进行转换，从而到达终点，此时匹配过程完成。

预处理时间O(M)

最坏匹配时间复杂度O(N*M)

[cpp]  view plain copy

1. /*  
2.  * ===  FUNCTION  ====================================================================== 
3.  *         Name:  bitap  
4.  *         Description:  bitap method. 
5.  *======================================================================================= 
6.  */  
7. int bitap(const char *text, const char *find)  
8. {  
9.     if (text == '/0' || find == '/0')  
10.         return -1;  
11.     int text_len = strlen(text);  
12.     int find_len = strlen(find);  
13.     if (text_len < find_len)  
14.         return -1;  
15.     int i = 0;  
16.     int j = find_len - 1;  
17.     char map[find_len + 1];  
18.     map[0] = 1;  
19.     for (i=1; i<=find_len; i++)  
20.     {  
21.         map[i] = 0;  
22.     }  
23.     for (i=0; i< text_len; i++)  
24.     {  
25.         for (j=find_len-1; j>=0; j--)  
26.         {  
27.             map[j+1] = map[j] & (text[i] == find[j]);  
28.         }  
29.         if (map[find_len] == 1)  
30.         {  
31.             return i - find_len + 1;  
32.         }  
33.     }  
34.     return -1;  
35. }  

 

注意：Bitap匹配算法中可以改用位移操作实现，从而将匹配复杂度从O(N*M)降低到O(N)。

 

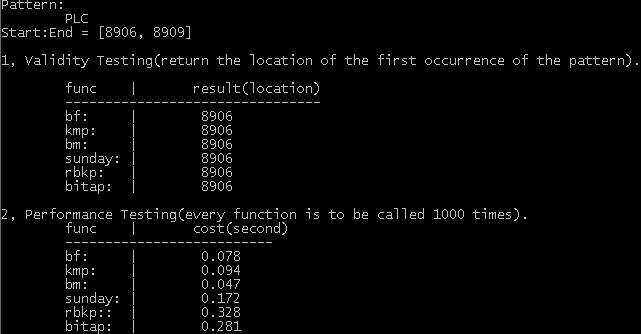
总结，以上算法中，性能较好的为KMP，BM, 实现简单的为BF，Sunday，Bitap。两者折中来看，KMP表现较好。

预处理时间 匹配时间复杂度

BF O(0)  O(N*M)

KMP O(M)  O(N)

BM O(N+M^2)O(N)

Sunday O(M)O(N*M)

Robin-Karp O(0)O(N*M)

Bitap O(M)  O(N*M)->O(N)

 

以上六种算法比较实现的代码如下所示（其中string长度10000）。