Tencent 2016校招研发岗笔试题

昨天听曾主任说起今天腾讯的一道笔试题，于是今天就上网搜了一下，搜出一道去年Tencent的笔试题，源自于 2016校招腾讯研发岗笔试题（第二题），感觉挺有意思，自己也做了一下。

Analysis

题目如下：

写成方程组的形式：

$$\begin{align} a_1 +a_2-9=4 \tag 1 \\ a_4-a_5 \times a_6=4 \tag 2 \\ a_7+a_8 - a_9 = 4 \tag 3 \\ a_1+a_4 \div a_7=4 \tag 4 \\ a_2-a_5\times a_8=4 \tag 5 \\ 9-a_6-a_9=4 \tag 6 \end{align}$$

有8个待求未知数，但有6个方程，故此方程有无数组解，不妨先考虑求解整数解。先固定两个未知数，即把它当做已知数：$a_1$、$a_7$
由(1)式可得：

$$a_2=13-a_1$$
注意到，由于所有的未知数都是在 0~100之间，所以， $a_1、a_2$范围为 $[0, 13]$。
而且，在实际编程求解时。此时的 $a_2$是算出值的，可以当做已知，用来求解下一个未知数。
根据 (4)式，可知：
$$a_4=a_7 \times (4-a_1)$$
由此更进一步的确定 $a_1$的范围： $[0, 4]$
由 (5)式得：
$$a_8=\frac{a_2-4}{a_5}$$
再联合 (2)、(5)两式：
$$a_2+a_4-a_5 \times (a_8 + a_6)=8$$
由此可得：
$$a_6+a_8=\frac{a_2+a_4-8}{a_5} \tag a$$
联合 (3)(6)两式可得：
$$a_6+a_7+a_8=9 \tag b$$
因此， $a_6、a_7、a_8$的范围在 $[0,9]$，且：
$$a_6+a_8=9-a_7$$
联立 (a)式，得到：
$$a_5=\frac{a_2+a_4-8}{9-a_7}$$
由 (2)式，得 $a_6$：
$$a_6=\frac{(a_4-4)\cdot (9-a_7)}{a_2+a_4-8}$$
往下很容易得：
$$a_8=\frac{a_2-4}{a_5}$$
$$a_9=5-a_6$$

至此，已经完成方程组未知数的逐步求解，前面求解的未知数是求解后面未知数的必要条件。通过对$a_1、a_7$的迭代来完成求解，且$a_1、a_7$有大致的范围：

$$a_1 \in [0,4]\\ a_7 \in [0,9]$$

Implement

于是，用C++实现程序如下：

#include<iostream>
using namespace std;

int main()
{
    double a1, a2;
    double a3 = 9;
    double a4, a5, a6;
    double a7, a8, a9;

    for(a1 = 0; a1 <= 4; a1 = a1 + 1)
    {
        for(a7 = 0; a7 <= 9; a7 = a7 + 1)
        {
            a2 = 13 - a1;
            a4 = a7 * (4 - a1);

            a5 = (a2 + a4 - 8) / (9 - a7);
            if (a5 > 100 || a5 < 0)
                continue; 

            a6 = (a4 - 4) * (9 - a7) / (a2 + a4 -8);
            if (a6 > 100 || a6 < 0)
                continue; 

            a8 = (a2 - 4) / a5;
            if (a8 > 100 || a8 < 0)
                continue;

            a9 = 5 - a6; 
            if (a9 > 100 || a9 < 0)
                continue;

            cout << "a1: " << a1 << " " <<"a2: " << a2 << " " <<"a3: " << a3 << endl;
            cout << "a4: " << a4 << " " <<"a5: " << a5 << " " <<"a6: " << a6 << endl;
            cout << "a7: " << a7 << " " <<"a8: " << a8 << " " <<"a9: " << a9 << endl << endl;

        }
    }
}

Result

执行结果如下：

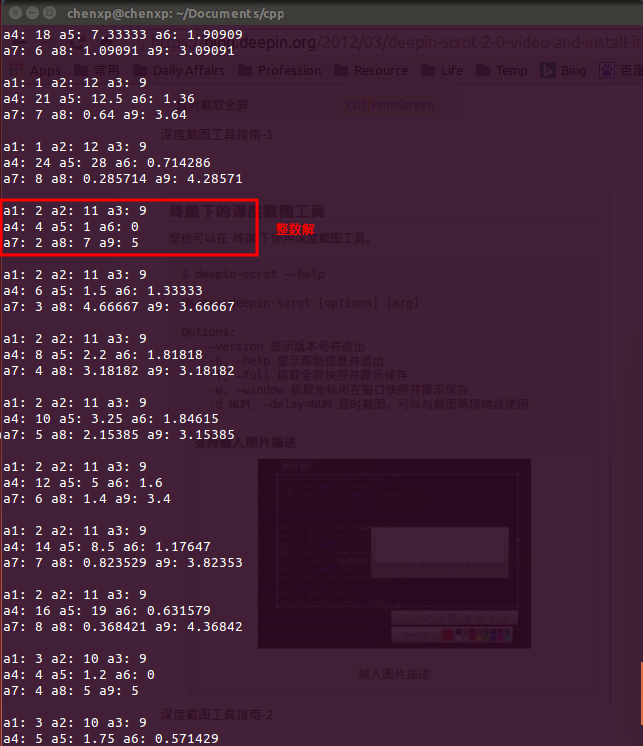
满足条件的整数解就一组，小数解很多。
综上，本题实际上就是一道数学题，只不过因为方程组里面含有二次项。所以，要避免求解二次方程，所以在选择固定未知数的时候要注意。

Reference

1. http://ask.julyedu.com/question/716
2. http://blog.csdn.net/u010660138/article/details/48266297