矩阵链乘法
•给定一个由n个矩阵构成矩阵序列(链)<A1, A2, ..., An>,要将它们相乘(假定它们按此序列是乘法相容的:Ai是pi-1×pi矩阵,而Ai+1是pi×pi+1矩阵),计算积:
A1A2 ... An•只要对此序列加上括号,确定运算顺序,就可以算得它们的积。矩阵链的积称为是完全加括号的,若它或是单一的矩阵,或是两个完全加括号的矩阵子链之积,并用一对括号括起来。
1.问题的理解与描述
•输入:数组<p0, p1, …, pn>,其中pi-1和pi分别是矩阵Ai的行数和列数,i=1, 2, …, n。
•输出:计算积A1A2 … An的最优完全加括号形式。
2.最优子结构
•假定Ai Ai+1… Aj的最优完全加括号在Ak及Ak+1之间分裂。则该加括号的“前缀”子链Ai Ai+1… Ak在Ai Ai+1… A j的此最优加括号中的完全加括号必为Ai Ai+1… Ak的最优加括号。
•设m[i, j]为计算矩阵所需的最少标量乘法次数,根据上面的最优子结构的讨论,我们有:
┌ 0 如果i = j
m[i,j] = │
└ min(i≤k<j) {m[i,k] + m[k+1,j] + Ai.row*Ak.col*Aj.col} 如果i < j3.算法的伪代码描述
MATRIX-CHAIN-ORDER(p)
n ← length[p] - 1
for i ← 1 to n
do m[i, i] ← 0
for l ← 2 to n //l 是矩阵链的长度
do for i ← 1 to n - l + 1
do j ← i + l - 1
m[i, j] ← ∞
for k ← i to j - 1
do q ← m[i, k] + m[k + 1, j] + pi-1 pkpj
if q < m[i, j]
then m[i, j] ← q
s[i, j] ← k
return m and s- 代码实现
4.1 C语言版
pair.h file
#ifndef _PAIR_H
#define _PAIR_H
#ifdef __cplusplus
extern "C" //告诉编译器{ }内部是用C写成的文件,请用C的方式来连接他们
{
#endif
typedef struct
{
void* first;
void* second;
}pair;
pair make_pair(void*f, void*d);
pair matrixChainOrder(int *p, int n);
void printOptimalParens(int *s, int i, int j, int n);
#ifdef __cplusplus
}
#endif
#endifpair.c file
#include <stdlib.h>
#include <stdio.h>
#include<limits.h>
#include "pair.h"
pair make_pair(void*f, void*d)
{
pair p = { f, d };
return p;
}
pair matrixChainOrder(int *p, int n)
{
int i, l, j, k, q;
int *m = (int*)malloc((n + 1)*(n + 1)*sizeof(int));//m 存储最小标量乘法次数
int *s = (int*)malloc((n + 1)*(n + 1)*sizeof(int));//s:存储最优解表格
for (i = 0; i <= n; i++)
m[i*(n + 1) + i] = 0;//m[i][i]=0
for (l = 2; l <= n ; l++)//l 为子矩阵链的长度
for (i = 1; i <= n - l + 1;i++)
{
j = i + l - 1;
m[i*(n + 1) + j] = INT_MAX;//m[i,j]=∞
for (k = i; k <= j - 1;k++)
{
q = m[i*(n + 1) + k] + m[(k + 1)*(n + 1) + j] + p[i - 1] * p[k] * p[j];
if (q<m[i*(n+1)+j])
{
m[i*(n + 1) + j] = q;
s[i*(n + 1) + j] = k;
}
}
}
return make_pair(m, s);
}
void printOptimalParens(int *s, int i, int j, int n)
{
if (i == j)
printf("A%d",i);
else
{
printf("(");
printOptimalParens(s, i, s[i*(n + 1) + j],n);
printOptimalParens(s, s[i*(n + 1) + j] + 1, j,n);
printf(")");
}
}main.c file
#include <stdio.h>
#include <stdlib.h>
#include "pair.h"
int main(int argc, char ** argv)
{
int p[] = { 30, 35, 15, 5, 10, 20, 25 };
int *s, *m;
pair r = matrixChainOrder(p, 6);
m = (int*)r.first;
s = (int*)r.second;
printOptimalParens(s, 1, 6, 6);
printf("\n the min muilty times is: %d \n", m[13]);
free(s);
free(m);
system("pause");
return (EXIT_SUCCESS);
}4.2 C++版
matrixchain.cpp fiel
#include "stdafx.h"
#include "matrixchain.h"
#include <climits>
pair<int*, int*>matrixChainOrder(int*p, int n)
{
long i, l, j, k, q;
int *m = new int[(n + 1)*(n + 1)];
int *s = new int[(n + 1)*(n + 1)];
for (i = 1; i <= n; i++)
m[i*(n + 1) + i] = 0;//m[i,i]=0
for (l = 2; l <= n; l++)
for (i = 1; i <= n - l + 1;i++)
{
j = i + l - 1;
m[i*(n + 1) + j] = INT_MAX;
for (k = i; k <= j - 1;k++)
{
q = m[i*(n + 1) + k] + m[(k + 1)*(n + 1) + j] + p[i - 1] * p[k] * p[j];
if (q<m[i*(n+1)+j])
{
m[i*(n + 1) + j] = q;
s[i*(n + 1) + j] = k;
}
}
}
return make_pair(m, s);
}
void printOptimalParens(int *s, int i, int j, int n)
{
if (i == j)
cout << 'A' << i;
else
{
cout << '(';
printOptimalParens(s, i, s[i*(n + 1) + j], n);
printOptimalParens(s, s[i*(n + 1) + j] + 1, j, n);
cout << ')';
}
}matrixchain.h fiel
#ifndef _MATRIXCHAIN_H
#define _MATRIXCHAIN_H
#include <iostream>
using namespace std;
pair<int*, int*> matrixChainOrder(int*p, int n);
void printOptimalParens(int *s, int i, int j, int n);
#endifmain.cpp file
#include "stdafx.h"
#include "matrixchain.h"
int _tmain(int argc, _TCHAR* argv[])
{
int p[] = { 30, 35, 15, 5, 10, 20, 25 };
int *s, *m;
pair<int*,int*> r = matrixChainOrder(p, 6);
m = r.first;
s = r.second;
printOptimalParens(s, 1, 6, 6);
cout << endl << m[13] << endl;
delete[]s;
delete[]m;
system("pause");
return 0;
}
- 运行结果:








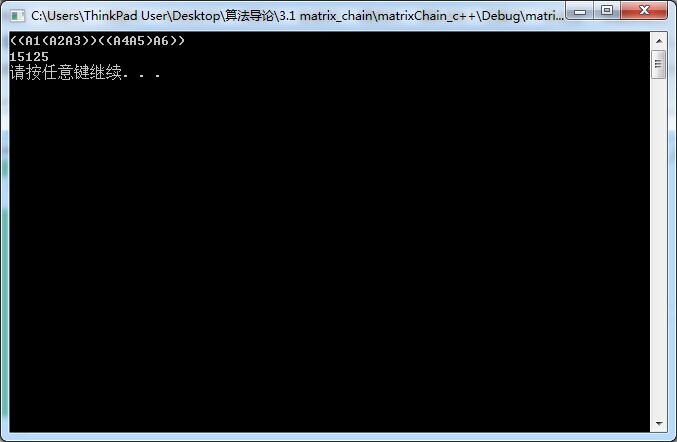














 1583
1583

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








