题外话：本人为研三学渣，最近因为要写文章以及实习工作需要开始接触高大上的机器学习，好几年没碰数学好多都忘记，最近花了几天时间开始看了机器学习的入门方法，想用自己笨拙的理解方式为大家解释一下线性回归以实现方式，希望可以帮助那些还在这个大门外徘徊的同学们以最通俗的方式去理解什么叫线性回归，后面我会尽量把自己的学习过程都写下来，希望得到大神们的指正和建议，也希望和大家多交流共同学习（ps:第一次写博客，写的不好勿喷，技术大牛们别嫌我写的简单笨拙 哈哈
一、什么叫线性回归
其实一开始我也不知道，哈哈！！百度上是这么写的：线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。
都说万事开头难，如果是数学基础比较好的同学估计立马就能理解了，那么我们如何理解这个线性回归呢？我已经用红色的字体把这句话关键的部分标出来了，是来确定俩种过两种以上的变量的关系，好，那么我们就从这里开始，什么两种以上！以上会不会比较复杂啊，那么我们就假设就两种，x和y好了吧，假设我们有组数据:
x={1,6,2,5,67,43,23,11,89,34,45}
x
=
{
1
,
6
,
2
,
5
,
67
,
43
,
23
,
11
,
89
,
34
,
45
}
y={5,15,7,13,137,89,49,25,181,71,93}
y
=
{
5
,
15
,
7
,
13
,
137
,
89
,
49
,
25
,
181
,
71
,
93
}
x和y是一一对应的，先撇开数据的物理意义，我就从这组数据开始，假设我们就是找规律，找出x与y的对应关系，那么我们就可以预测再给我一个x我就能知道对应y是少了对不对，如果我们把上述数据的x和y一一对应组成点(x,y)绘制到直角坐标系中话你会看到下面一张图，哎？这不是一条直线么（废话，因为数据是自己编的呀，开个玩笑，哈哈）
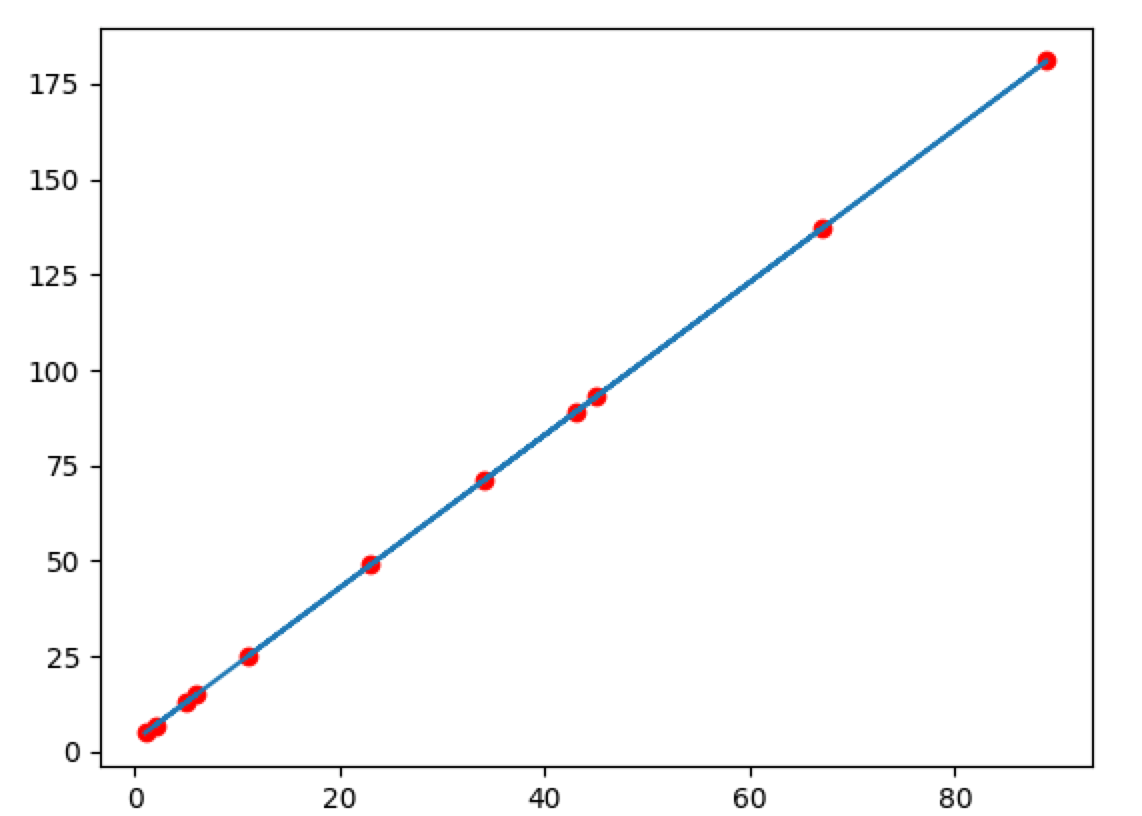
那么我可以看到x和y组成的点是分布在一条直线上的，纵轴为y，横轴为x，那么我们现在就可以假设y和x的关系是一阶线性关系，也就是y和x可以用 y=a∗x+b y = a ∗ x + b ，这个大家应该都知道，那么接下来我们要做的是一个什么事情呢，为了确定这条直线是哪条直线，我们就需要求出a和b，正常我们是把点带入进这个方程就可以，俩个变量只要两个方程组就ok，对不对，针对上述列出的数据来看，带入俩个点的确就可以求出a和b，不过在实际案例中，这些点不可能都是刚刚好落在一条直线上的，多多少少都会有偏差，比如看下面这个图:
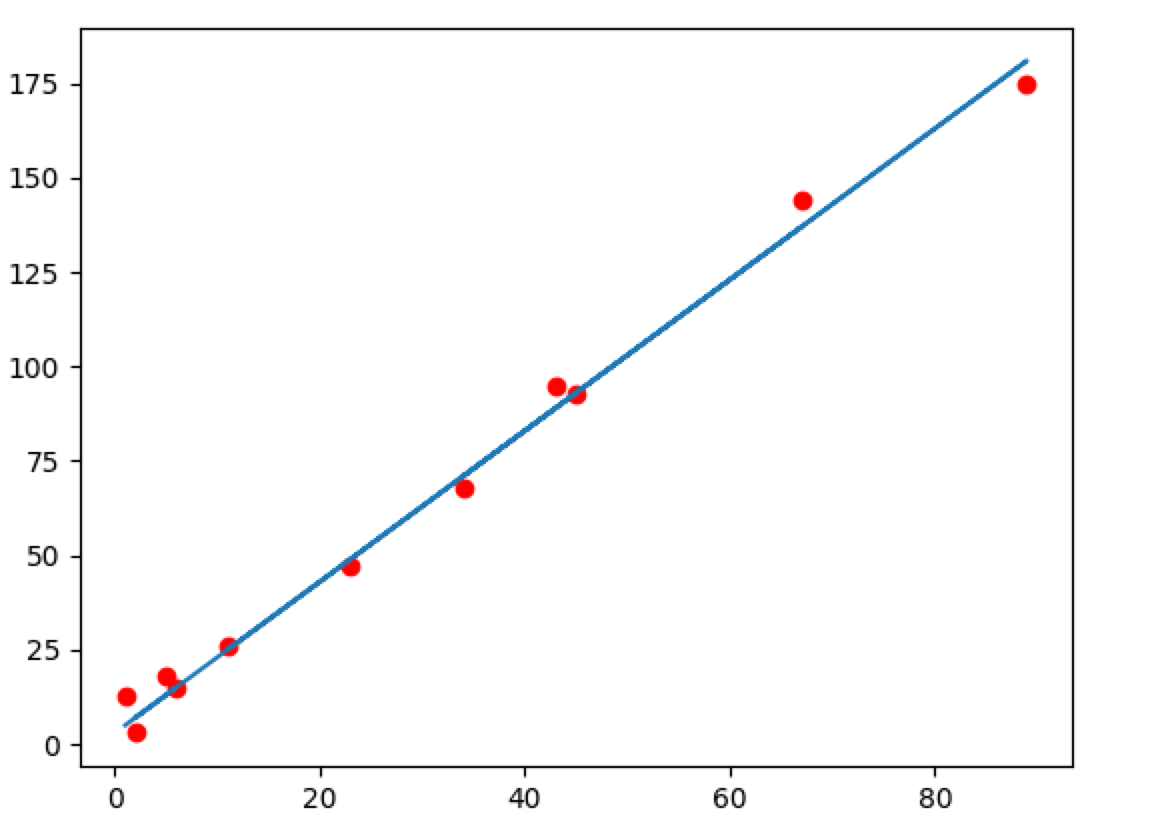
这个时候点是分布在 y=a∗x+b y = a ∗ x + b 两边的，这个时候你用某俩个点带入进入求出的来点就不一定使用于第三个点来，这个时候我们该怎么确定a和b呢？假设上面的数据集合x和y是我们采集的数据和观察的结果，x我们称之为样本集，y为结果集，x的个数我们称为样本数量，上面我们x集合中有11个数据我先称作，x1,x2,x3,x4…x11,我们分别把他们带入到 y=a∗x+b y = a ∗ x + b ，可以得到y’1,y’2,y’3,y’4…y’5,那么现在得到y’就是我们通过假设的这条直线算出来的值，至于对不对，准不准确呢，肯定和实际的y是有误差的，这是不是代表如果y’和y的差距越小我们的直线表述y和x的关系就越准确呢？答案是肯定的，那么我们的误差怎么表示呢？这个时候我们引入一个误差函数，就把这个函数叫cost吧，当然你叫error也行:
error=(y1−y′1)2+(y2−y′2)2+(y3−y′3)2+...+(y11−y′11)2
e
r
r
o
r
=
(
y
1
−
y
′
1
)
2
+
(
y
2
−
y
′
2
)
2
+
(
y
3
−
y
′
3
)
2
+
.
.
.
+
(
y
11
−
y
′
11
)
2
我们可以看到每一项都是实际值与我们的估计值之间的差，当然这个error是有学名的，好像叫残差，哈哈，我也忘记了，回头找个书看看应该就知道。如果我们估计的好的话，那么估计值和实际值应该是一样的，那么error不就是0了那么，不过理想总是丰满的，现实总是残酷的，万一不能十全十美怎么办，那么我们就让这个error尽量的小呗，那么这就是一个求极值的问题啦？完了，这个极值怎么求呢。。。。（黑人问号脸），这个方法就多了，伟大的前人数学家们都为我们铺了好几百年路，方法我就不一一列举了（因为好多我也不会。。。。。。慢慢学吧），就直接看最热门的方法是怎么做的吧，请看下一节。
二、梯度下降
相信大家在很多地方听说过梯度下降，那么到底什么是梯度下降呢？首先我们来理解一个概念什么是梯度，我们直接上例子，我们有个函数
z=f(x,y)
z
=
f
(
x
,
y
)
这是一个二元函数，我们假设z是在平面区域上具有一阶连续偏导数的，那么对任意一个点(x,y),我们可以得到:
对x的偏导数为:
∂f∂x
∂
f
∂
x
对y的偏导数为:
∂f∂y
∂
f
∂
y
那么由这两个值我们可以得到一个向量记作
∇f(x,y)=(∂f∂x,∂f∂y)
∇
f
(
x
,
y
)
=
(
∂
f
∂
x
,
∂
f
∂
y
)
这个向量有什么用呢？当我们带改变x和y的值得时候我们知道z的值肯定也是会随之变化的，也就是说当x和y沿着这个梯度方向变化的时候z值改变的是最大的，而对x的偏导数就是x变化的变化率，对y的偏导数是y变化的变化率。有了这个梯度的概念我们来说说梯度下降。
现在我们先回到上一章中我们得出的error这个公式
error=(y1−y′1)2+(y2−y′2)2+(y3−y′3)2+...+(y11−y′11)2
e
r
r
o
r
=
(
y
1
−
y
′
1
)
2
+
(
y
2
−
y
′
2
)
2
+
(
y
3
−
y
′
3
)
2
+
.
.
.
+
(
y
11
−
y
′
11
)
2
因为 y=w∗x+e y = w ∗ x + e , 那么：
error=(y1−wx1−e)2+(y2−wx2−e)2+(y3−wx3−e)2+...+(y11−wx11−e)2
e
r
r
o
r
=
(
y
1
−
w
x
1
−
e
)
2
+
(
y
2
−
w
x
2
−
e
)
2
+
(
y
3
−
w
x
3
−
e
)
2
+
.
.
.
+
(
y
11
−
w
x
11
−
e
)
2
这个时候我们怎么把我们这个error函数和梯度联系起来呢，这里我尽量推导的详细点，数学好的小伙伴可以略过，我们知道这个时候x1、x2…x11以及y1、y2…y11都是已知的，而w和e则是我们的未知数，那么我们可以令 error=z=f(w,e) e r r o r = z = f ( w , e ) 此时:
∇error=(∂f∂w,∂f∂e)
∇
e
r
r
o
r
=
(
∂
f
∂
w
,
∂
f
∂
e
)
这个时候我们不就可以用上面的梯度公式了嘛，下面我们就要开始求偏导数了。
那么导数相信很多同学在高中时期就已经学过，最基础的导数我就不详细说明了，实际可以用极限的思想去推导，有兴趣的小伙伴可以复习一下高数。我下面要提的一点可能大家听说过，我读高中的时候我们老师把这个叫做复合函数求导，怎么说看下面：
如果我们有
f(x)=(x2−1)2
f
(
x
)
=
(
x
2
−
1
)
2
,如果我们不开方，乍一看这个函数我们是无法根据基本的求导法则来求出导数的，这个时候我们来看我们的目标,我们的目标是求出
∂f∂x=?
∂
f
∂
x
=
?
(这里一元函数的的导数和偏导是一样的)
我们令 g(x)=x2−1 g ( x ) = x 2 − 1 ,那么
f(g(x))=g2(x)
f
(
g
(
x
)
)
=
g
2
(
x
)
所以
∂f∂g(x)=2g(x)−−−−−−(1)
∂
f
∂
g
(
x
)
=
2
g
(
x
)
−
−
−
−
−
−
(
1
)
∂g∂x=2x−−−−−−−(2)
∂
g
∂
x
=
2
x
−
−
−
−
−
−
−
(
2
)
由(1)(2)可以得到
∂f∂g(x)∗∂g∂x=∂f∂x=2g(x)2x=2(x2−1)2x=4∗(x2−1)x
∂
f
∂
g
(
x
)
∗
∂
g
∂
x
=
∂
f
∂
x
=
2
g
(
x
)
2
x
=
2
(
x
2
−
1
)
2
x
=
4
∗
(
x
2
−
1
)
x
好的记住这个，很有用，未来我想应该也很有用，虽然我还没看到后面，但是我知道以后这个会有高大上的名字，不再叫复合函数求导了，哈哈（链式法则？）。
回到我们的error函数
error=z=f(w,e)=(y1−wx1−e)2+(y2−wx2−e)2+(y3−wx3−e)2+...+(y11−wx11−e)2
e
r
r
o
r
=
z
=
f
(
w
,
e
)
=
(
y
1
−
w
x
1
−
e
)
2
+
(
y
2
−
w
x
2
−
e
)
2
+
(
y
3
−
w
x
3
−
e
)
2
+
.
.
.
+
(
y
11
−
w
x
11
−
e
)
2
我们要求
∂f∂w和∂f∂e
∂
f
∂
w
和
∂
f
∂
e
针对
(y1−wx1−e)2
(
y
1
−
w
x
1
−
e
)
2
这一项令
g(w)=(−x1w−e+y1)
g
(
w
)
=
(
−
x
1
w
−
e
+
y
1
)
f1=(y1−wx1−e)2
f
1
=
(
y
1
−
w
x
1
−
e
)
2
那么
∂f1∂g(w)∂g∂w=∂f1∂w=2g(w)(−x1)=2(wx1+e−y1)∗x1
∂
f
1
∂
g
(
w
)
∂
g
∂
w
=
∂
f
1
∂
w
=
2
g
(
w
)
(
−
x
1
)
=
2
(
w
x
1
+
e
−
y
1
)
∗
x
1
∂f1∂g(e)∂g∂e=∂f1∂w=2g(w)(−x1)=2(wx1+e−y1)
∂
f
1
∂
g
(
e
)
∂
g
∂
e
=
∂
f
1
∂
w
=
2
g
(
w
)
(
−
x
1
)
=
2
(
w
x
1
+
e
−
y
1
)
同理，我们可以令
f2=(y2−wx1−e)2...f11=(y11−wx11−e)2
f
2
=
(
y
2
−
w
x
1
−
e
)
2
.
.
.
f
11
=
(
y
11
−
w
x
11
−
e
)
2
那么
∂f∂w=∂f1∂w+∂f2∂w+∂f3∂w+...+∂f11∂w
∂
f
∂
w
=
∂
f
1
∂
w
+
∂
f
2
∂
w
+
∂
f
3
∂
w
+
.
.
.
+
∂
f
11
∂
w
∂f∂e=∂f1∂e+∂f2∂e+∂f3∂e+...+∂f11∂e
∂
f
∂
e
=
∂
f
1
∂
e
+
∂
f
2
∂
e
+
∂
f
3
∂
e
+
.
.
.
+
∂
f
11
∂
e
至此我们的对于我们针对上述数据的的梯度我们已经求完了，下面我们来说说梯度下降算法，根据上述梯度的概念我们可以知道，当w和e沿着
∇error=∇f(w,e)=(∂f∂w,∂f∂e)]
∇
e
r
r
o
r
=
∇
f
(
w
,
e
)
=
(
∂
f
∂
w
,
∂
f
∂
e
)
]
方向变化时，error的变化是最快的，我们的目的是让error最小，那么我们可以尝试一下方法：
1)给w和e设定一个初始值
2不断改变w和e的值，并且满足error递减，直到达到我们一个我们满意的最小值，此时的w和e就是我们最佳的参数w和e，这个算法我们叫做梯度下降。
那么这个w和e如何调整呢？当w和e沿着
∇error=∇f(w,e)=(∂f∂w,∂f∂e)
∇
e
r
r
o
r
=
∇
f
(
w
,
e
)
=
(
∂
f
∂
w
,
∂
f
∂
e
)
方向变化时可以让我们更快的到达error的满意值。
w:=w−α∂f∂w
w
:=
w
−
α
∂
f
∂
w
e:=e−α∂f∂e
e
:=
e
−
α
∂
f
∂
e
这个里的:=是赋值不是不是等号
我们在编程实现梯度下降的时候就可以根据这个俩个公式来进行迭代。
三、归纳
最后我们归纳一下，我们研究很多问题都会从特殊到一般，下面我们来看一下有n个特征的线性回归的情况。
假设我们有m个样本,n个特征：
x1=x11,x12,x13....x1n<=>y1=y11,y12,y13....y1n
x
1
=
x
1
1
,
x
2
1
,
x
3
1
.
.
.
.
x
n
1
<=>
y
1
=
y
1
1
,
y
2
1
,
y
3
1
.
.
.
.
y
n
1
x2=x21,x22,x23....x2n<=>y2=y21,y22,y23....y2n
x
2
=
x
1
2
,
x
2
2
,
x
3
2
.
.
.
.
x
n
2
<=>
y
2
=
y
1
2
,
y
2
2
,
y
3
2
.
.
.
.
y
n
2
......
.
.
.
.
.
.
xm=xm1,xm2,xm3....xmn<=>ym=ym1,ym2,ym3....ymn
x
m
=
x
1
m
,
x
2
m
,
x
3
m
.
.
.
.
x
n
m
<=>
y
m
=
y
1
m
,
y
2
m
,
y
3
m
.
.
.
.
y
n
m
若我们有拟合函数
h(θ)=θ0+θ1x1+θ2x2+...+θn∗xn
h
(
θ
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
∗
x
n
误差函数
J(θ)=1/2∗∑i=0mhθ(xi−yi)2
J
(
θ
)
=
1
/
2
∗
∑
i
=
0
m
h
θ
(
x
i
−
y
i
)
2
那么我们根据上述的梯度下降算法可以确定出所有的参数 θj θ j 即
θj:=θ−α∗∂J(θ)∂θj
θ
j
:=
θ
−
α
∗
∂
J
(
θ
)
∂
θ
j
因为手头正在做golang的事情，就用golang实现了一下 h(x)=3∗x1+4∗x2+3 h ( x ) = 3 ∗ x 1 + 4 ∗ x 2 + 3
import (
"fmt"
)
var(
theata []float64
step = 0.0001
x_train = [][]float64{
{1,3},{2,4},{3,0},{4,1},{2,5},{6,5},{11,3},{2,9},{8,10},{1,5},{6,7},{8,9},{0,2},
}
y_train = []float64{18,25,12,19,29,41,48,45,67,26,49,63,11}
)
//h(x)=3*x1+4*x2+3
func init(){
theata = make([]float64,3)
theata[0] = 1.0
theata[1] = 1.0
theata[2] = 1.0
}
func h(x []float64) float64{
return theata[0]*x[0]+theata[1]*x[1]+theata[2]
}
func main(){
for i:=0;i<100000;i++{
sum0 := 0.0
sum1 := 0.0
sum2 := 0.0
for j:=0;j<13;j++{
sum0 = sum0 + step * (y_train[j] - h(x_train[j])) * x_train[j][0]
sum1 = sum1 + step * (y_train[j] - h(x_train[j])) * x_train[j][1]
sum2 = sum2 + step * (y_train[j] - h(x_train[j]))
}
fmt.Println(theata[0],theata[1],theata[2])
theata[0] = theata[0] + sum0
theata[1] = theata[1] + sum1
theata[2] = theata[2] + sum2
}
fmt.Println(theata[0],theata[1],theata[2])
}
扫一扫
183
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
