机器学习入门：逻辑回归的原理与实现

最新推荐文章于 2024-07-24 09:14:07 发布

一介草民-小王

最新推荐文章于 2024-07-24 09:14:07 发布

阅读量1.8k

点赞数

文章标签：人工智能机器学习线性回归梯度下降

本文链接：https://blog.csdn.net/u010270285/article/details/79307778

版权

前言

继上一次写了一下自己在学习线性回归中的一些见解和公式推导之后，得到了同学们和同事的一些评论和鼓励，让我更加有动力去把自己所了解和学习的东西写下来，最近因为写博客还学会了很多markdown的知识，很开心，今天我就准备从原理上为大家讲解一下逻辑回归的原理和知识概要，以及实现。

一、什么是逻辑回归

这里需要跟大家区分一下的时候，逻辑回归和前面线性回归有些区别，逻辑回归解决的是分类问题，通常这个分类是一个二分类问题，当然也可以是多分类，不过我们还是老规矩，从一般到复杂，我们就从二分类问题开始讨论。

同样的我们先开始构造数据，首先我们需要有一个训练集，如果说我们下面一堆点(后面贴上点数据)

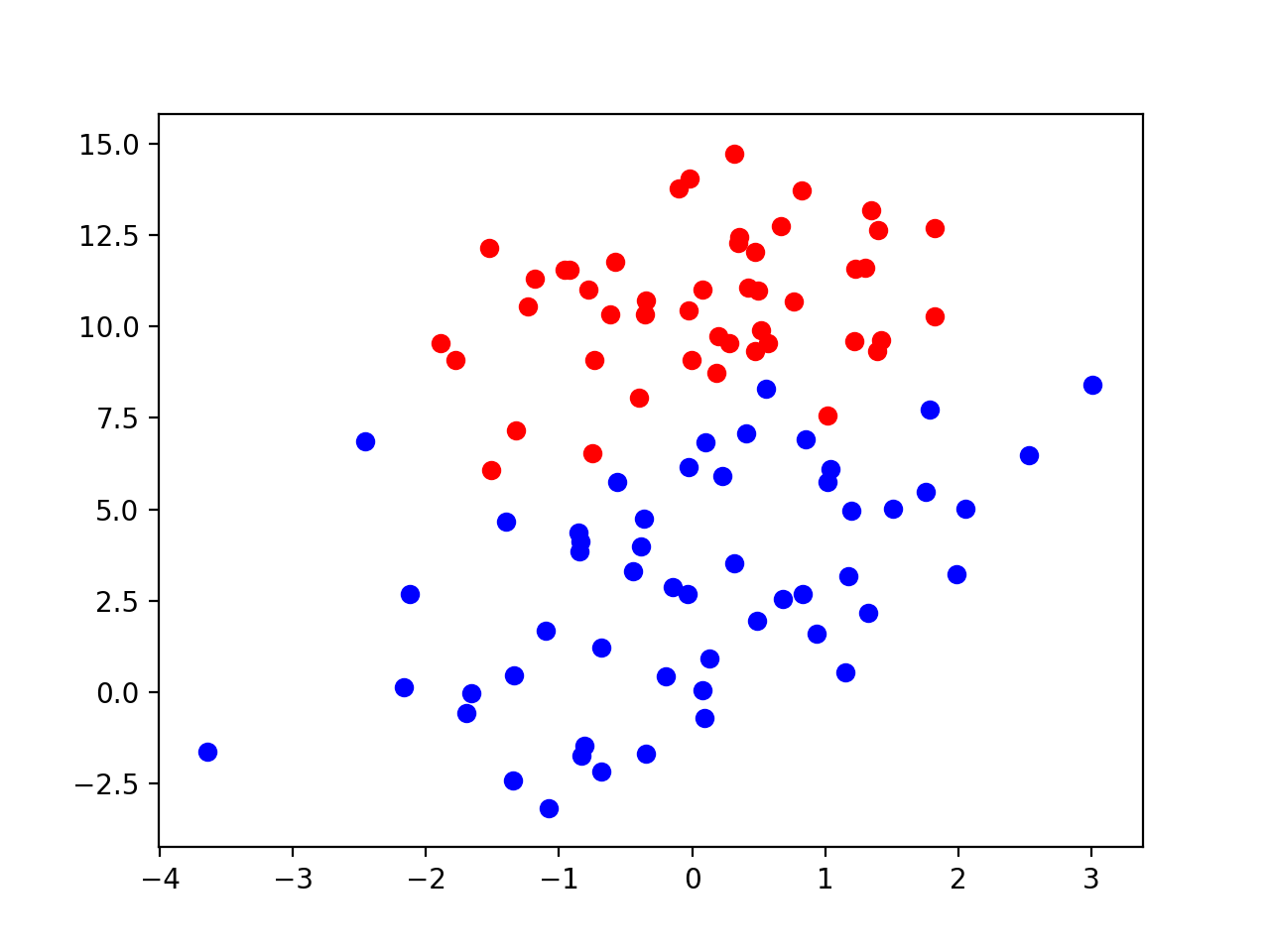
我们可以看到红色的点为一类，蓝色的点为一类，我们现在希望有一个规则可以尽可能多的把这俩类点分开，下面我们逻辑回归要做的工作就是根据这个训练集，训练出我们需要的这个规则。这里我们规定红色点的类为1，蓝色点的类为0，我们把所有的红色蓝色的点都归到一个点集合

D = {p 0 (x 0 0, x 0 1), p 1 (x 1 0, x 1 1), p 2 (x 2 0, x 2 1) . . ., p n (x n 0, x n 1)}

$D = \{p_0(x_00,x_01),p_1(x_10,x_11),p_2(x_20,x_21)...,p_n(x_n0,x_n1)\}$
每个点对应类集合

H = {h 0, h 1, h 2, h 3, h 4 . . . ., h n}

$H=\{h_0,h_1,h_2,h_3,h_4....,h_n\}$

hn h n $h_n$ 的取值为0或1（我们的前提是二分问题）
可以看到，经过这个集合训练之后，给我们一个新的点

pn+1(xn+10,xn+11) p n + 1 ( x n + 1 0 , x n + 1 1 ) $p_{n+1}(x_{n+1}0,x_{n+1}1)$ ,我们要判读它属于哪一类，也就是判断

hn+1 h n + 1 $h_{n+1}$ 取值是0还是1，那么从集合

D D $D$ 到集合

H

$H$ 之间是否存在一种关系呢？
我们令:

z = θ 0 * x 0 + θ 1 * x 1

$z=\theta_0*x_0 + \theta_1*x_1$
这里我们可以知道，这个时候

z z $z$ 的取值范围为整个自然数集，我们怎么将

z

$z$ 映射为取值为0和1呢？这里我们伟大的前人已经为我们铺好了路，我们来看下面这个函数:

S (x) = 1 1 + e - x

$S(x)=\frac{1}{1+e^{-x}}$
这个函数有什么用呢？我们首先来考察这个函数的图像

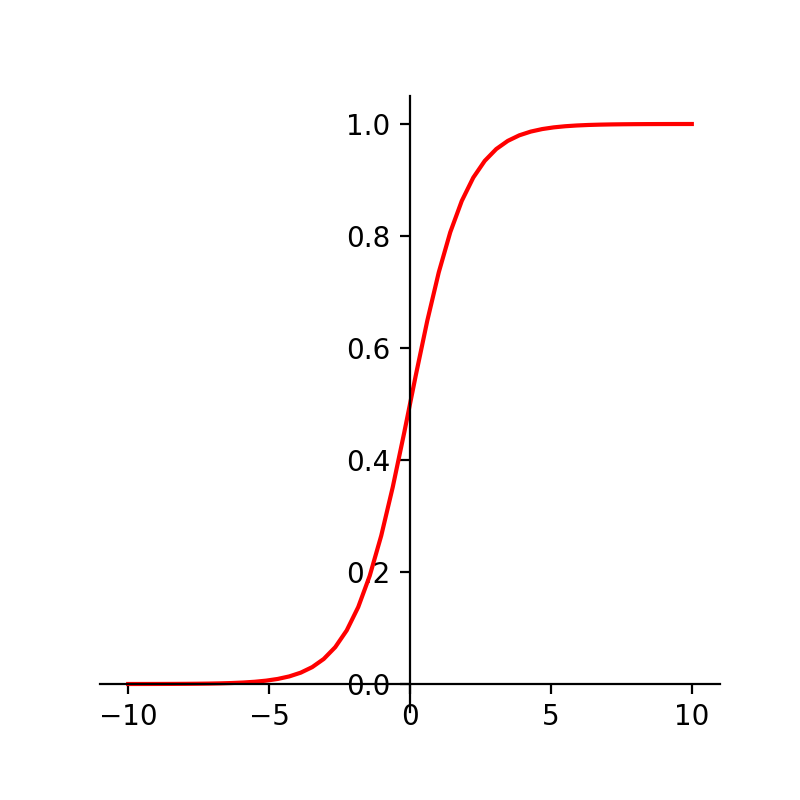
假设横轴坐标为

z z $z$ 纵轴坐标为h,那么我们就可以找到z到一个h的一个对应关系:

h (z) = \frac{1}{1 + e^{- z}}

$h(z)= \frac{1}{1+e^{-z}}$
由函数图像可以得到h的取值范围为[0,1],这样就可以将z映射到[0,1],而我们h的取值为1或者0，这时我们通常会设定一个阈值，例如当z=0时，h的值为0.5，所以当h大于0.5时，我们认为是1类，当h小于0.5时，我们认为0类。那么我们就得到了逻辑回归的数学模型

h (z) = 1 1 + e - z

$h(z)=\frac{1}{1+e^{-z}}$
其中：

z = \sum i = 1 n θ i * x i

$z=\sum_{i=1}^{n}\theta_i*x_i$
那么

h θ (x) = 1 1 + e - \sum n i = 0 θ i * x i

$h_\theta(x)=\frac{1}{1+e^{-\sum_{i=0}^{n}\theta_i*x_i}}$
构建好我们的逻辑回归模型，和线性回归模型同样的，我们需要构建一个代价函数去对我们的训练数据进行训练，使得我们训练的模型参数最优化(即代价函数求极值)，下面讨论逻辑回归的代价函数之前，为了让大家可以更好的理解这个代价函数的由来和公式推导，下面会先为大家介绍一个数学方法：极大似然估计(MLE)

二、极大似然估计与代价函数

极大似然估计说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。可以为大家举一个生活中的一个例子让大家去理解这个概念。
假如我们有个盒子里面有红白两种颜色的球，我们从盒子里面取十次球，每次取球后放回，记录十次球的颜色，七次红色三次白色，这时以我们的生活经验去估计盒子里面红色球和白色球的比例是7:3，那么这个估计的理论依据是什么呢？假设抽到红球的概率为 $p$ ，则抽到白球的概率为 $1-p$ ,那么取球十次，七次红色三次白色的联合概率为：

L = p 7 * (1 - p) 3

$L=p^{7}*(1-p)^{3}$
为了支持我们7:3的假设，就得使得“取球十次，七次红色三次白色”这个事件的概率最大，即L的概率最大，这是我们就可以对L求导可以得到:

L' = 7 * p 6 * (1 - p) 3 - 3 * p 7 * (1 - p) 2

$L^\prime=7*p^{6}*(1-p)^{3}-3*p^{7}*(1-p)^{2}$
令

L' = 0

$L^\prime = 0$
即

7 * (1 - p) - 3 * p = 0

$7*(1-p)-3*p=0$
此时解出

p=0.7 p = 0.7 $p=0.7$ ,也就是红色球与白色球的比例为7:3。
那么刚刚的这个例子又和我们的逻辑回归有什么关系呢？因为

hθ(x) h θ ( x ) $h_\theta(x)$ 的取值为[0,1]，也就表明x属于某一类别的概率，那么x属于1类别的概率为：

p (y = 1 | x, θ) = h θ (x)

$p(y=1|x,\theta)=h_\theta(x)$
x属于0类别的概率为：

p (y = 0 | x, θ) = 1 - h θ (x)

$p(y=0|x,\theta)=1-h_\theta(x)$
将上面两式统一起来可以得到样本的概率函数为:

p (y | x, θ) = h θ (x) y * (1 - h θ (x)) 1 - y

$p(y|x,\theta)=h_\theta(x)^{y}*(1-h_\theta(x))^{1-y}$
假设此时我们有n的特征m个样本，因为这m样本相互独立，所以m个样本的联合概率为:

L (θ) = \prod i = 0 m p (y (i) | x (i)) = \prod i = 0 m h θ (x (i)) y (i) * (1 - h θ (x (i))) 1 - y (i)

$L(\theta)=\prod_{i=0}^{m}p(y^{(i)}|x^{(i)})=\prod_{i=0}^{m}h_\theta(x^{(i)})^{y^{(i)}}*(1-h_\theta(x^{(i)}))^{1-y^{(i)}}$
那么

L(θ) L ( θ ) $L(\theta)$ 就是此时的似然函数了,和刚刚上面我们举的例子一样，下面我们就需要去估计出最有的参数

θ θ $\theta$ 。这里的符号

∏ ∏ $\prod$ 为连乘符号，当我们对

L(θ) L ( θ ) $L(\theta)$ 进行求解时发现比较复杂，此时我们可以对等式两边取自然对数，这个时候我们并不会改变函数的单调性(至于为什么有兴趣的朋友可以自己去证明一下，这里就不证明了),取自然对数,连乘就变成了连加：

l (θ) = l n L (θ) = l n (\prod i = 0 m h θ (x (i)) y (i) * (1 - h θ (x (i))) 1 - y (i))

$l(\theta)=lnL(\theta)=ln(\prod_{i=0}^{m}h_\theta(x^{(i)})^{y^{(i)}}*(1-h_\theta(x^{(i)}))^{1-y^{(i)}})$

l (θ) = \sum i = 1 m y (i) l n h θ (x (i)) + (1 - y (i)) l n (1 - h θ (x (i)))

$l(\theta)=\sum_{i=1}^{m}y^{(i)}lnh_\theta(x^{(i)})+(1-y^{(i)})ln(1-h_\theta(x^{(i)}))$
我们令：

J (θ) = - 1 m l (θ)

$J(\theta)=-\frac{1}{m}l(\theta)$
这里

J(θ) J ( θ ) $J(\theta)$ 就是我们逻辑回归的代价函数了，下面我们就需要通过求导的方式来求当

J(θ) J ( θ ) $J(\theta)$ 取极值时候参数

θ θ $\theta$ 的取值。

三、梯度下降求解

和线性回归一样的，我们可以利用梯度下降的方式去进行迭代求解得到最优解，这里就不再重复梯度下降了。梯度下降第一步我们就需要求梯度，也就是需要进行求导。
展开 $l(\theta)$ 可以得到:

l (θ) = y (1) l n h θ (x (1)) + (1 - y (1)) l n (1 - h θ (x 1)) + . . . . . . . + y (m) l n h θ (x (m)) + (1 - y (m)) l n (1 - h θ (x m))

$l(\theta)=y^{(1)}lnh_\theta(x^{(1)})+(1-y^{(1)})ln(1-h_\theta(x^{1}))+.......+y^{(m)}lnh_\theta(x^{(m)})+(1-y^{(m)})ln(1-h_\theta(x^{m}))$
此时我们考擦其中一项:

l (1) (θ) = y l n h θ (x) + (1 - y) l n (1 - h θ (x)) - - - - - - - （ 1 ）

$l^{(1)}(\theta)=ylnh_\theta(x)+(1-y)ln(1-h_\theta(x))-------（1）$

\partial l ( 1 ) \partial θ j = y \partial l n h θ ( x ) \partial θ j + (1 - y) \partial l n ( 1 - h θ ( x ) ) \partial θ j - - - - - - （ 2 ）

$\frac{\partial l^{(1)} }{\partial \theta_j}=y\frac{\partial lnh_\theta(x)}{\partial \theta_j}+(1-y)\frac{\partial ln(1-h_\theta(x))}{\partial \theta_j}------（2）$

\partial l n h θ ( x ) \partial θ j = \partial l n h θ ( z ) \partial θ j = 1 h θ ( z ) \cdot \partial h θ ( z ) \partial z \cdot \partial z \partial θ j - - - - - - - （ 3 ）

$\frac{\partial lnh_\theta(x)}{\partial \theta_j} =\frac{\partial lnh_\theta(z)}{\partial \theta_j} =\frac{1}{h_\theta(z)}\centerdot\frac{\partial h_\theta(z)}{\partial z} \centerdot \frac{\partial z}{\partial \theta_j} -------（3）$

\partial ( 1 - h θ ( x ) ) \partial θ j = \partial ( 1 - h θ ( z ) ) \partial θ j = 1 1 - h θ ( z ) \cdot \partial ( 1 - h θ ( z ) ) \partial z \cdot \partial z \partial θ j - - - - （ 4 ）

$\frac{\partial (1-h_\theta(x))}{\partial \theta_j} =\frac{\partial (1-h_\theta(z))}{\partial \theta_j} =\frac{1}{1-h_\theta(z)}\centerdot\frac{\partial (1- h_\theta(z))}{\partial z} \centerdot \frac{\partial z}{\partial \theta_j}----（4）$
因为:

hθ(z) h θ ( z ) $h_\theta(z)$ 是为sigmod函数，所以：

\partial h θ ( z ) \partial z = h θ (z) (1 - h θ (z)) - - - - - - （ 5 ）

$\frac{\partial h_\theta(z)}{\partial z}=h_\theta(z)(1-h_\theta(z))------（5）$

\partial ( 1 - h θ ( z ) ) \partial z = - \partial h θ ( z ) \partial z = - h θ (z) (1 - h θ (z)) - - - - - （ 6 ）

$\frac{\partial (1-h_\theta(z))}{\partial z} = -\frac{\partial h_\theta(z)}{\partial z}=-h_\theta(z)(1-h_\theta(z))-----（6）$
将(5)带入(3)、(6)带入(4) 可以得到

\partial h θ ( x ) \partial θ j = (1 - h θ (z)) x j - - - - (7)

$\frac{\partial h_\theta(x)}{\partial \theta_j} = (1-h_\theta(z))x_j ----(7)$

\partial ( 1 - h θ ( x ) ) \partial θ j = - h θ (z) x j - - - - - (8)

$\frac{\partial (1-h_\theta(x))}{\partial \theta_j} =-h_\theta(z)x_j-----(8)$
将(7)(8)俩式带入到（2）得到

\partial l ( 1 ) \partial θ j = y (1 - h θ (z)) x j - (1 - y) h θ (z) x j = (y - h θ (x)) x j

$\frac{\partial l^{(1)} }{\partial \theta_j}=y(1-h_\theta(z))x_j-(1-y)h_\theta(z)x_j=(y-h_\theta(x))x_j$
同理

\partial l ( i ) \partial θ j = y (i) (1 - h θ (z)) x j - (1 - y (i)) h θ (z) x j = (y (i) - h θ (x (i))) x j

$\frac{\partial l^{(i)} }{\partial \theta_j}=y^{(i)}(1-h_\theta(z))x_j-(1-y^{(i)})h_\theta(z)x_j=(y^{(i)}-h_\theta(x^{(i)}))x_j$
所以:

\partial l ( θ ) \partial θ j = \sum i = 1 m (y (i) - h θ (x (i))) x j

$\frac{\partial l(\theta) }{\partial \theta_j}=\sum_{i=1}^{m}(y^{(i)}-h_\theta(x^{(i)}))x_j$
那么

\partial J ( θ ) \partial θ j = - 1 m \sum i = 1 m (y (i) - h θ (x (i))) x j

$\frac{\partial J(\theta) }{\partial \theta_j}=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}-h_\theta(x^{(i)}))x_j$
则梯度下降就可以按照：

θ j : = θ j - α \cdot \partial J ( θ ) \partial θ j = θ j - α \cdot 1 m \sum i = 1 m (h θ (x) - y (i)) x j

$\theta_j:=\theta_j-\alpha \centerdot\frac{\partial J(\theta) }{\partial \theta_j} =\theta_j-\alpha \centerdot\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x)-y^{(i)})x_j$

下面是点数据和代码，这里数据是摘自互联网。

-1.395634    4.662541    1
-0.752157    6.538620    0
-1.322371    7.152853    0
0.423363    11.054677    0
0.406704    7.067335    1
0.667394    12.741452    0
-2.460150    6.866805    1
0.569411    9.548755    0
-0.026632    10.427743    0
0.850433    6.920334    1
1.347183    13.175500    0
1.176813    3.167020    1
-1.781871    9.097953    0
-0.566606    5.749003    1
0.931635    1.589505    1
-0.024205    6.151823    1
-0.036453    2.690988    1
-0.196949    0.444165    1
1.014459    5.754399    1
1.985298    3.230619    1
-1.693453    -0.557540    1
-0.576525    11.778922    0
-0.346811    -1.678730    1
-2.124484    2.672471    1
1.217916    9.597015    0
-0.733928    9.098687    0
-3.642001    -1.618087    1
0.315985    3.523953    1
1.416614    9.619232    0
-0.386323    3.989286    1
0.556921    8.294984    1
1.224863    11.587360    0
-1.347803    -2.406051    1
1.196604    4.951851    1
0.275221    9.543647    0
0.470575    9.332488    0
-1.889567    9.542662    0
-1.527893    12.150579    0
-1.185247    11.309318    0
-0.445678    3.297303    1
1.042222    6.105155    1
-0.618787    10.320986    0
1.152083    0.548467    1
0.828534    2.676045    1
-1.237728    10.549033    0
-0.683565    -2.166125    1
0.229456    5.921938    1
-0.959885    11.555336    0
0.492911    10.993324    0
0.184992    8.721488    0
-0.355715    10.325976    0
-0.397822    8.058397    0
0.824839    13.730343    0
1.507278    5.027866    1
0.099671    6.835839    1
-0.344008    10.717485    0
1.785928    7.718645    1
-0.918801    11.560217    0
-0.364009    4.747300    1
-0.841722    4.119083    1
0.490426    1.960539    1
-0.007194    9.075792    0
0.356107    12.447863    0
0.342578    12.281162    0
-0.810823    -1.466018    1
2.530777    6.476801    1
1.296683    11.607559    0
0.475487    12.040035    0
-0.783277    11.009725    0
0.074798    11.023650    0
-1.337472    0.468339    1
-0.102781    13.763651    0
-0.147324    2.874846    1
0.518389    9.887035    0
1.015399    7.571882    0
-1.658086    -0.027255    1
1.319944    2.171228    1
2.056216    5.019981    1
-0.851633    4.375691    1

python代码实现：

import matplotlib.pyplot as plt
import numpy as np

theta=np.array([1.0,1.0,1.0])
alpha=0.0001
def sigmod(x):
    return 1.0/(1+np.exp(-z(x)))
def z(x):
    return x[0]*theta[0]+x[1]*theta[1] +theta[2]


data = np.loadtxt('/Users/wangcong/data.txt')
x_data = data[:, 0:2]
y_data = data[:,2]

for (i,x) in enumerate(x_data):
    if y_data[i]==1:
        plt.scatter(x[0],x[1],c='r')
    else:
        plt.scatter(x[0],x[1],c='b')

for i in range(100000):
    sum_0 = 0.0
    sum_1 = 0.0
    sum_2 = 0.0
    for x,y in zip(x_data,y_data):
        sum_0 -= alpha*(sigmod(x)-y)*x[0]
        sum_1 -= alpha*(sigmod(x)-y)*x[1]
        sum_2 -= alpha*(sigmod(x)-y)
    theta[0] += sum_0
    theta[1] += sum_1
    theta[2] += sum_2

def y(x):
    return (-theta[2]-x*theta[0])/theta[1]

y_line = y(x_data[:,0])
plt.plot(x_data[:,0],y_line)
plt.show()

训练结果：
这里写图片描述

一介草民-小王

关注

0
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
机器学习入门：逻辑回归的原理与实现

前言继上一次写了一下自己在学习线性回归中的一些见解和公式推导之后，得到了同学们和同事的一些评论和鼓励，让我更加有动力去把自己所了解和学习的东西写下来，最近因为写博客还学会了很多markdown的知识，很开心，今天我就准备从原理上为大家讲解一下逻辑回归的原理和知识概要，以及实现。一、什么是逻辑回归这里需要跟大家区分一下的时候，逻辑回归和前面线性回归有些区别，逻辑回归解决的是分...
复制链接

扫一扫