自由曲线以及圆锥曲线

曲线

光滑曲线

定义

当曲线上的每一点处都有切线，并且切线随切点的移动而连续转动，这样的曲线称为光滑曲线。

充分条件

• 设平面曲线$C$由参数方程$x=x(t),y=y(t),t\in [\alpha ，\beta ]$给出。若$x(t)$与$y(t)$在[α，β]上连续可微。$x\prime (t)$与$y\prime (t)$不同时为零，即$x^{\prime }(t{)}^2+y^{\prime }(t{)}^2\ne 0,t\in [\alpha ,\beta ]$，则称$C$一条光滑曲线。

  $y=x^3$对应的参数曲线$x=t,y=t^3,t\in [\alpha ，\beta ]$，虽然不满足$x^{\prime }(0{)}^2+y^{\prime }(0{)}^2\ne 0,t\in [\alpha ,\beta ]$，但该曲线是光滑的

• 若函数$f(x)$在区间$[\alpha ,\beta ]$内具有一阶连续导数，则其对应的图形称之为光滑曲线。

  $y=f(x)=\sqrt{R^2-x^2},x\in [-R,R]$的参数方程可以表示为$x=R\cos (t),y=R\sin (t),t\in [-R,R]$，由参数方程可得知其为光滑曲线。但$y^{\prime }=f^{\prime }(x)=-\frac{x}{\sqrt{R^2-x^2}},x\in [-R,R]$在$-R$,$R$处不连续。

曲率

曲线的弯曲程度，切线转角与弧长关系的微分绝对值，即切线转角$\Delta \alpha$与弧长$\Delta s$之比的绝对值。记作$K={\lim }_{\Delta s\to 0}|\frac{\Delta \alpha }{\Delta s}|$。

设曲线方程为$y=f(x)$，曲率公式为$K=\frac{y^{\prime \prime }}{(1+{y^{\prime }}^2{)}^{\frac{3}{2}}}|x=x_0$

设曲线是参数方程$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}|t\in [\alpha ，\beta ]$，曲率公式为$K=\frac{x^{\prime }(t)y^{\prime \prime }(t)-x^{\prime \prime }(t)y^{\prime }(t)}{[x^{\prime }(t{)}^2+y^{\prime }(t{)}^2{]}^{\frac{3}{2}}}$

相关概念引申

曲线上点$M$处的曲率倒数称作曲线在改点的曲率半径，记作$\rho$，$\rho =\frac{1}{K}=\frac{(1+{y^{\prime }}^2{)}^{\frac{3}{2}}}{y^{\prime \prime }}|x=x_0$。

在点$M$处做曲率的法线的某一侧取点$D$，使得$|DM|=\rho$，以$D$为圆心，以$\rho$为半径作圆。该圆称作曲线在点$M$处的曲率圆（密切圆），圆心$D$称作曲线在M处的曲率中心。曲率中心$(a,b)$的计算公式$a=x_0-f^{\prime }(x_0)\frac{1+f^{\prime }(x_0{)}^2}{f^{\prime \prime }(x_0)}$，$b=f(x_0)+\frac{1+f^{\prime }(x_0{)}^2}{f^{\prime \prime }(x_0)}$

曲率圆（密切圆）与曲线在$M$邻近有相同的凹向。在实际设计计算中，常用密切圆在点$M$邻近的一段圆弧来近似代替曲线弧，以简化问题。

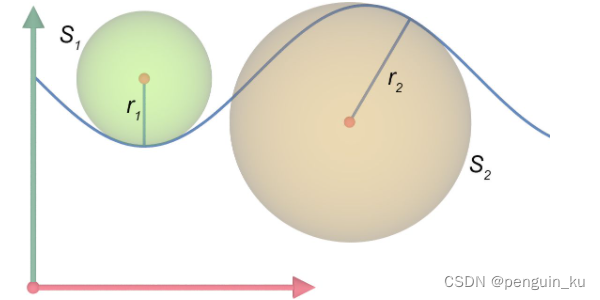
观察得知，圆上各点曲率半径为$R$（盲猜这是曲率半径名词的由来），直线上各点曲率半径为$+\infty$

应用

案例一

题目：使用圆柱形铣刀加工椭圆$\frac{x^2}{40^2}+\frac{y^2}{50^2}=1$工件，选用多大的铣刀可以得到好的效果？

解答：

• 通过观察，得知曲率最大的点位于$(0,\pm 50)$
• 选取$(0,50)$，计算曲率半径得到32
• 选用直径64的圆柱形铣刀可得到较好的效果

案例二

题目：激光加工时，即需要快也需要稳，如何实现

解答：

• 计算出各个点的曲率信息
• 速度规划时，使用曲率信息，即曲率大的地方速度规划小，曲率小的地方速度规划大

曲线数学理论

Weierstrass逼近定理

曲线是一种几何图形，由笛卡尔几何可得知，其必然对应一方程$f(x,y)=0$。

1885年Weierstrass提出逼近定理，1927年被美国数学家Stone首次证明，又称Stone-Weierstrass逼近定理：

• 设$f(x)$是$[a,b]$上的连续函数，则必存在多项式函数列$f_n(x)$，使得$f_n(x)$一致收敛于$f(x)$。
• 设$f(x)$是$[a,b]$上的周期性连续函数，则必可用三角函数级数一致逼近。（傅里叶变换Fourier Transform）

$$y=f(x)=\sum _{i=0}^n{a}_i{f}_i(x)=\left[\begin{array}{cccc}{a}_0& a_1& \dots & a_n\end{array}\right]\left[\begin{array}{c}{f}_0(x)\\ f_1(x)\\ ⋮\\ f_n(x)\end{array}\right]=\left[\begin{array}{cccc}{a}_0& a_1& \dots & a_n\end{array}\right]\left[\begin{array}{c}{\beta }_{0,k}(x)\\ {\beta }_{1,k}(x)\\ ⋮\\ {\beta }_{n,k}(x)\end{array}\right]$$

${\beta }_{i,k}$表征序号$i$的不高于$k$次多项式。

曲线方程$f(x,y)=0$分析

• 单值方程：即一个$x$有唯一的$y$与之对应，可以直接表征为$y=f(x)$
• 多值方程：即一个$x$有多个的$y$与之对应，则可引入隐形参数$t$得到$f(x(t),y(t))=0$。从而演变成两个连续函数$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$（隐形参数函数同样适用单值方程）

至此，理论论证了对于任意曲线，均可以由多项式函数逼近。也即通过给定一组特征点可以由多项式函数表达一条曲线。

Bernstein伯恩施坦多项式

定义

Bernstein在证明Weierstrass逼近定理中深入研究，提出了伯恩施坦多项式
$$\{\begin{array}{l}{B}_n(t)={\sum }_{k=0}^n{b}_{k,n}(t)\\ b_k^n(t)=C_n^k{t}^k(1-t{)}^{n-k}\\ C_n^k=\frac{n!}{k!(n-k)!}|\frac{0}{0}=0\end{array}$$
从定义中可以得知共有$n+1$个伯恩施坦多项式基函数，为方便起见，令$b_i^n=0|\forall i<0\bigcup \forall i>n$

基函数概率解释

做独立可重复一个实验，成功的概率是$t$。若连续重复$n$次，正好成功 $k$次的概率。

该理解可以得知${\lim }_{n\to \infty }{b}_k^n(t)$仅在$k/n=t$时达到峰值（图中为$t=0.4$），并且快速向两侧衰减，该性质称之为尖峰，是非常重要的特性。

由于这种性质，Bernstein多项式可以很自然地组合成近似于$[0,1]$上的任何连续函数。给定这样一个函数$f$，定义一个近似值$Bn[f]$为$B_n[f](t)={\sum }_{k=0}^{n}f(\frac{k}{n})b_{n,k}(t)$，且随着 $n\to \infty$，该多项式将一致收敛到原函数$f$（即证明了Weierstrass逼近定理）。

递归

$$\begin{array}{rl}{b}_k^n(t)& =C_n^k{t}^k(1-t{)}^{n-k}\\ & =\left(C_{n-1}^k+C_{n-1}^{k-1}\right)t^k(1-t{)}^{n-k}\\ & =C_{n-1}^k{t}^k(1-t{)}^{n-k}+C_{n-1}^{k-1}{t}^k(1-t{)}^{n-k}\\ & =(1-t)C_{n-1}^k{t}^k(1-t{)}^{n-1-k}+t{C}_{n-1}^{k-1}{t}^{k-1}(1-t{)}^{(n-1)-(k-1)}\\ & =(1-t)b_k^{n-1}(t)+t{b}_{k-1}^{n-1}(t)\end{array}$$

伯恩斯坦多项式基函数的幂基表达

由于幂基$t^0,t^1,t^2,\dots ,t^n$构成了次数小于或等于$n$的多项式泛函空间，所以任何一个$n$次伯恩斯坦多项式基函数都可以用幂基表示。

将牛顿二项式定理即$(x+y{)}^n={\sum }_{i=0}^n{C}_n^i{x}^i{y}^{n-i}$代入伯恩斯多项式基函数得到
$$\begin{array}{rl}{b}_k^n(t)& =C_n^k{t}^k(1-t{)}^{n-k}\\ & =C_n^k{t}^k\sum _{i=0}^{n-k}{1}^{n-i}{C}_{n-k}^i(-t{)}^i\\ & =C_n^k{t}^k\sum _{i=0}^{n-k}(-1{)}^i{C}_{n-k}^i{t}^i\\ & =\sum _{i=0}^{n-k}(-1{)}^i{C}_n^k{C}_{n-k}^i{t}^{i+k}\\ & =\sum _{i=k}^n(-1{)}^{i-k}{C}_n^k{C}_{n-k}^{i-k}{t}^i\\ & =\sum _{i=k}^n(-1{)}^{i-k}{C}_n^i{C}_i^k{t}^i\end{array}$$

矩阵表达

由递归公式，可以得知，伯恩施坦多项式可以由一组伯恩施坦基函数的线性组合
$$\begin{array}{rl}B(t)& =\sum _{k=0}^n{a}_k{b}_k^n(t)\\ & =\left[\begin{array}{cccc}{b}_0^n(t)& b_1^n(t)& \dots & b_n^n(t)\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]\\ & =\left[\begin{array}{cccc}{t}^0& t^1& \dots & t^n\end{array}\right]\left[\begin{array}{ccccc}{b}_0^0& 0& 0& \dots & 0\\ b_0^1& b_1^1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ b_0^n& b_1^n& b_2^n& \cdots & b_n^n\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]\end{array}$$

特性

此处没搞明白

• $b_k^n(t)|t\in [0,1]$非负性
• 单位剖分性
• 升阶

Bezier曲线

1959年。当时就职于雪铁龙的法国数学家Paul de Casteljau开始对Bernstein多项式进行了图形化的尝试，并且提供了一种数值稳定的算法，实现很少的控制点生成复杂的平滑曲线。1962年，雷诺工程师Pierre Bézier使用该方法辅助汽车车体工业设计得名Bezier曲线。

贝塞尔为伯恩施坦多项式的应用（理论到应用，大部分情况下会做各种近似替换的尝试处理）。

推导

已知光滑曲线经过$P_0,P_1,\dots ,P_n$

设该曲线表征的函数为$f(t)=\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$

则使用伯恩施坦多项式逼近$B_n[f](t)={\sum }_{k=0}^{n}f(\frac{k}{n})b_k^n(t)$，

由伯恩施坦的尖峰特性，即$li{m}_{n\to +\infty }{b}_k^n(t)=\{\begin{array}{l}{P}_K,\frac{k}{n}=t\\ 0,\frac{k}{n}\ne t\end{array}$

可代入得到$B(t)={\sum }_{k=0}^n{P}_k{b}_k^n(t)$。

令$P_k{b}_k^n(t)=P_k^n(t)$

进一步简化$B(t)={\sum }_{k=0}^n{P}_k^n(t)$

de Casteljau递归

模仿伯恩施坦递归$b_k^n(t)=(1-t)b_k^{n-1}(t)+t{b}_{k-1}^{n-1}(t)$，de Casteljau提出贝塞尔的递归$P_k^n(t)=(1-t)P_k^{n-1}(t)+t{P}_{k+1}^{n-1}(t)$，设定$P_k^0(t)=P_k$。

对于上面的表达式，采用下图表示（图片盗自https://zhuanlan.zhihu.com/p/263749820）

上图最左侧为特征多边形的点（控制点）列表。

特性

• $n+1$个控制点生成$n$阶Bezier曲线
• 过首尾点，只逼近其他控制点，但不过。（引导过程中使用了$n\to +\infty$，但实际上并不满足，且递归方程也发生了变异【此处的变异充满神奇】）
• Bezier曲线完全落在包含所有控制点的最小凸多边形内（在运动控制系统中，用于贝塞尔轨迹的碰撞检查的简化，否则需要采样，极度耗时）
• 改变任意一个控制点，整条$Bezier$曲线都会相应改变，但控制点对于附近影响最大，越远的点影响越小
• 仿射不变性：Bezier控制点与Bezier曲线在整个坐标平面的仿射变换$x\to Ax+b$下（如旋转、平移等）均保持不变。（此处引出对称性）
• 任意直线与Bezier曲线的交点个数，不超过该直线与控制多边形的交点个数

感性理解

N阶贝塞尔，表征点$t\in [0,1]$时间内由第一个点走到最后一个点（也有做割角理解的），即如下图（网络盗图）

在t时刻，由控制点$P_0,P_1$得到$P_{10}$，由控制点$P_1,P_2$得到$P_{11}$，$P_{10},P_{11}$得到$P_{20}$，经过$n$次得到$n$阶贝塞尔$t$时刻的坐标。

B-Splines

样条

样条曲线是由给定的一组点而得到的一条光滑曲线。根据曲线经过这些给定的点还是逼近，分为插值样条和逼近样条。其数学核心在于使用分段低阶多项式连接组合表达连续的复杂曲线以取代高阶多项式组合（贝塞尔是高阶多项式，拉格朗日多项式也是高阶多项式，即随着点的变多，次数越来越高）。

插值样条

• 介绍

  最初，样条曲线都是借助于物理样条得到的，放样员把富有弹性的柔性物体（细木条），用压铁固定在曲线应该通过的给定型值点处，样条做自然弯曲所绘制出来的曲线就是样条曲线。样条曲线不仅通过各有序型值点，并且在各型值点处的一阶和二阶导数连续，也即该曲线具有连续的、曲率变化均匀的特点。

• 数学表达

已知待插值函数$f(x)$，已知节点$x_0,\dots ,x_n$的函数值，按照相邻节点分段，获得$n$个插值区间，每个区间内使用$k$次多项式$s_i(x)$插值，使其满足插值条件与$k-1$阶平滑性（$k-1$阶导数连续）：
{ S i ( x i ) = f ( x i ) , S i ( x i + 1 ) = f ( x i + 1 ) , 0 ≤ i ≤ n − 1 S i ( j ) ( x i + 1 ) = S i + 1 ( j ) ( x i + 1 ) , 0 ≤ i ≤ n − 2 , 1 ≤ j ≤ k − 1 ∣ x ∈ { x 0 , … , x n } \begin{cases}S_i(x_i)=f(x_i),S_i(x_{i+1})=f(x_{i+1}),0\le i\le n-1\\S_i^{(j)}(x_{i+1})=S_{i+1}^{(j)}(x_{i+1}),0\le i\le n-2,1\le j \le k-1\end{cases}|x\in \{x_0,\ldots,x_n\} {Si​(xi​)=f(xi​),Si​(xi+1​)=f(xi+1​),0≤i≤n−1Si(j)​(xi+1​)=Si+1(j)​(xi+1​),0≤i≤n−2,1≤j≤k−1​∣x∈{x0​,…,xn​}

• 应用场景

  • 音频设计、视频融合、动画设计、动画融合、各种渲染效果融合
  • 机械加工：补偿的曲线、速度曲线

• 基函数$S_i(x_i)$选择以及求解示例

  • 三次样条（盗图https://zhuanlan.zhihu.com/p/82619415）
    
    对于$n+1$个节点$x_0,\dots ,x_n$一共$n$个分段，即$4n$个未知数。其中每个分段两端的值已知，即存在$2n$个方程。因为一阶二阶导数连续，拥有$2(n-1)$个方程。还剩下两个条件，即$x_0,x_n$的一阶二阶导数。此处存在不同设定

    • 自然边界：$s^{\prime \prime }(x_0)=s^{\prime \prime }(x_n)=0$
    • $Not-a-knot$：$\{\begin{array}{l}{s}^{\prime \prime \prime }(x_0)=s^{\prime \prime \prime }(x_1)\\ s^{\prime \prime \prime }(x_{n-1})=s^{\prime \prime \prime }(x_n)\end{array}$
    • 固定边界：$\{\begin{array}{l}{s}^{\prime }(x_0)=c_1\\ s^{\prime }(x_n)=c_2\end{array}$
    • 周期样条：$\{\begin{array}{l}{s}^{\prime }(x_0)=s^{\prime }(x_n)\\ s^{\prime \prime }(x_0)=s^{\prime \prime }(x_n)\end{array}$

  对于多项式拟合，需要选择基函数，通过求解$Ax=B$计算基函数前面的系数。如果选择的基函数为 { 1 , x , x 2 , x 3 } \{1,x,x^2,x^3\} {1,x,x2,x3}，A矩阵为范德蒙矩阵，此时可能会遇到条件数过高，导致解不稳定（方程无解）。所以，需要选择合适的基函数。

  一般推荐
  $$\{\begin{array}{l}{C}_0(x)=x^2(3-2x)\\ c_1(x)=-x^2(1-x)\\ c_2(x)=(x-1{)}^{2}x\\ c_3(x)=2x^3-3x^2+1\end{array}|x\in [0,1]$$
  这组函数是线性不相关的。
  $$\{\begin{array}{l}{C}_0(1)=1,C_0^{\prime }(1)=0,C_0^{\prime }(0)=0,C_0(0)=0\\ C_1(1)=0,C_1^{\prime }(1)=1,C_1^{\prime }(0)=0,C_1(0)=0\\ C_2(1)=0,C_2^{\prime }(1)=0,C_2^{\prime }(0)=1,C_0(0)=0\\ C_3(1)=0,C_3^{\prime }(1)=0,C_3^{\prime }(0)=0,C_3(0)=1\end{array}$$

逼近样条

通过控制点，逼近样条。一般用来构造物体的表面。

样条曲线是由一组折线组成的多边形构造出来的。简单地说，以数值计算的方法，用光滑的参数曲线段逼近该折线多边形，构造出一条样条曲线。改变该多边形的顶点和个数，会影响曲线的形状。这里所说的折线多边形，即样条曲线的特征多边形或控制多边形。

• 样条曲线段
  样条曲线是由一组逼近控制多边形的光滑参数曲线段构成，这些曲线段就是样条曲线段。 特征多边形/控制多边形的顶点/控制点 构成特征多边形的各段折线的端点，就是特征多边形的顶点，也叫做控制多边形的控制点。只有在特殊情况下，样条曲线才能通过控制点。

• 编辑本段样条曲线的次数

  样条曲线的次数，是由样条曲线数学定义中所取的基函数所决定的。直观的说，所构成样条曲线的一段光滑参数曲线段，由控制多边形的相邻连续的几段折线段决定，就是几次样条，最常用的就是二次和三次样条。二次样条的某一曲线段只与相应的两段折线段，三个控制多边形顶点有关，改变其中一个顶点，将影响三段样条曲线段。同样的，对三次样条，某一曲线段由相应的三段折线段，四个控制点决定。

• 样条曲线的阶数(order)
  阶数与次数有关，样条曲线的阶是样条曲线的次数加一。样条曲线的阶越高，控制点越多。二次样条的阶数是三，样条曲线段与三个控制点决定；三次样条的阶数是四，样条曲线段与四个控制点决定。

• 样条曲线的权值
  权值可控制样条曲线段在控制多边形范围内做局部调整，反映了曲线靠近控制多边形的程度，权值越大，曲线段越靠近控制多边形。反之，则远离。当权值为1时，NURBS曲线退化为非有理B样条曲线，可见非有理B样条曲线是NURBS的一个子集。

• 样条曲线的允差
  允差是指样条曲线通过型值点的精确程度，允差越小，样条曲线与型值点越接近，允差为零，样条曲线将通过型值点。

B-Spline样条

背景

1946年I.J.Schoenberg提出一种基于样条的方法来近似曲线，他指出四种重要观点：傅里叶变换、截断多项式的差商、力学观点以及概率密度函数。

其动机来源于插值中的Runge-Kutta现象，即高阶多项式很容易产生不稳定的上下抖动。于是诞生采用分段低阶多项式通过连续的连接来代替高阶多项式。

1972年de Boor与Cox分别独立提出了b-spline的基函数公式。该公式称为deBoor-Cox公式。在此之前，基函数大多用差分方法计算，数值上不稳定。该公式为de Casteljau递归的的推广。

其克服了Bezier的缺陷:一旦确定了特征多边形的顶点数，就决定了曲线的阶数。当数据点的数量太多时，计算量急剧增加;无法做局部修改，这是一个很大的局限性，牵一发而动全身;光滑性很高，导致拼接比较复杂。

b-splines即基础样条。除此之外，样条还有其他类型，如Hermite splines

定义

p次B-Spline曲线由这些控制点和节点向量$U$定义，其公式为
$$\{\begin{array}{l}p(u)=\left[\begin{array}{cccc}{p}_0& p_1& \dots & p_n\end{array}\right]\left[\begin{array}{c}{B}_{0,k}(U)\\ B_{1,k}(U)\\ ⋮\\ B_{n,k}(U)\end{array}\right]={\sum }_{i=0}^n{p}_i{B}_{i,k}(u)\\ N_{i,1}(t)=\{\begin{array}{l}1,t_1\le x\le t_{i+1}\\ 0,Other\end{array}\\ N_{i,k}(t)=\frac{t-t_i}{t_{i+k-1}-t_i}{N}_{i，k-1}(t)+\frac{t_{i+k}-t}{t_{i+k}-t_{i+1}}{N}_{i+1,k-1}(t)\\ \frac{0}{0}=0\end{array}$$
即BSpline为Bezier的一般性推广，使用节点将$[0,1]$分割成$m$个区间。然后引入阶梯函数作为权重，从而控制特征多边形顶点（控制点）的影响范围。但因为此处影响范围是彼此重叠的，保证了整体曲线的k阶连续（所以B样条是一组Bezier拼接在一起只是一种简单但不准确的说法）。其Cox-de Boor递推图如下：

根据$N_{i,k}$的阶梯函数特性可以得知

• 基函数$N_{i,k}(t)$在$[t_i,t_{i+k}]$上非零
• 任何一个节点区间$[t_i,t_{i+1}]$，最多有$k$个$k-1$次的基函数非零，$N_{i-k+1,k}(t),N_{i-k+2,k}(t),\dots ,N_{i,k}(t)$
• 在重复度$r$的节点处，基函数$N_{i,k}(t)是C^{(k-r-1)}$阶连续的；
• 节点数=控制点数+次数+1.（阶数=次数+1，这一点和Bezier不同）
  

B-Spline特殊类型

均匀B样条：节点成等差数列分布。不具备断点性质（起始点和终止点并不等于第一个和最后一个控制点）

准均匀B样条：起始节点与终止节点具有K的重复度。中间节点称等差数列分布

分段Bezier曲线：起始节点与终止节点具有K的重复度，其他节点都具备k-1的重复度。即所有的曲线段都是Bezier曲线

非均匀B样条：任意分布的节点矢量，两端节点重复都不大于k，内节点重复都不大于$k-1$。

非均匀B样条的外延是包含了均匀、与准均匀、分段Bezier的外延的，而均匀、与准均匀、分段Bezier的外延式并列。

特性

• 局部支撑性：B样条诞生的目的。

• 权性：${\sum }_{i=0}^{n}N(i,k)(t)=1|t\in [t_i,t_{i+1}]$

• 连续性：在$r$重节点处的连续阶不低于$k-1-r$

• 凸包性：$P(t)$在区间$(t_i,t_{i+1})$上的部分位于$k$个点$[P_{i-k+1},Pi]$的凸包内。整个曲线位于各个凸包的并集内。

• 仿射不变性：仿射变换下$At=b$，表达式不变。

• 直线保持性：控制多边形退化为一条直线，曲线也退化为直线。

• 无法精确表达抛物线以外的二次曲线

一般来说，次数越高，则曲线的导数次数也会较高，那么将会有很多零点存在，较多的导数零点就导致原曲线存在较多的极值，使曲线出现较多的峰谷值;次数越低，样条曲线逼近控制点效果越好。另一方面，三次B样条曲线能够实现二阶导数连续，故最终选择准均匀三次B样条曲线作为轨迹规划的曲线比较合适。

有理B样条

非有理B样条无法精确表达抛物线意外的二次曲线。1975年美国锡拉丘兹大学的Versperille在有理B样条在非有理B样条的理论基础上为各个控制点拓展了权重，即权重控制$\omega$该控制点对于其影响范围内的曲线段的影响比例。

公式

$$P(t)=\frac{{\sum }_{i=0}^n{\omega }_i{P}_i{N}_{i,k}(t)}{{\sum }_{i=0}^n{\omega }_i{N}_{i,k}(t)}=\sum _{i=0}^n{P}_i{R}_{i,k}(t)$$

齐次坐标

引入齐次坐标，即$n$维空间的非有理B样条的控制点坐标用升$1$维的$n+1$维坐标来表征，其转换关系为$(x,y,z,\omega )\to (\frac{x}{\omega },\frac{y}{\omega },\frac{z}{\omega })$。从而权重的倒数作为齐次坐标的第$n$个元素。其逆转换关系为$(x,y,z,\omega )\to (\frac{x}{\omega },\frac{y}{\omega },\frac{z}{\omega })$。
$$P(t)=\frac{{\sum }_{i=0}^n{\omega }_i{P}_i{N}_{i,k}(t)}{{\sum }_{i=0}^n{\omega }_i{N}_{i,k}(t)}=\sum _{i=0}^n{P}_i^{\omega }{N}_{i,k}(t)$$

特性

有理B样条在非有理B样条的基础上增加了两个特性

• 透视不变性：在投影变换下产生正确的结果（而非有理B样条仅在仿射变换下产生准确的结果）
  

• 可以用来表示直线、二次曲线、非有理B样条曲线；并且，当推广到面片时，可以表示平面、二次曲面和复曲面

非有理B样条是有理B样条的子集。

1983年至1989年，Piegl与Tiller有理B样条的基础上做了深入研究，推广了NURBS。

非均匀有理B样条NURBS即有理非均匀B样条

圆锥曲线

• 概念定义：

  由一平面截二次锥面得到的曲线。圆锥曲线包括椭圆（圆为椭圆的特例）、抛物线、双曲线。2000多年前的古希腊数学家阿波罗尼斯（著作<<圆锥曲线>>与欧几里得的《几何原本》齐名）提出该概念。精妙之处在于二维曲线的研究升阶到三维空间（回想齐次坐标）。
  

• 数学定义：

  设一点$p_0(x_0,y_0)$，指定一直线

  到平面内一定点（焦点）的距离$r$与到定直线（准线）的距离$d$之比是常数（离心率）$e=r/d$的点的轨迹叫做圆锥曲线。

  • $e>1$：双曲线
  • $e=1$：抛物线
  • $0<e<1$：椭圆（圆为椭圆的一种）

总结

圆锥曲线是平面二次曲线的统一表达，NURBS是平面圆锥曲线与自由曲线的统一表达。OCC中针对不同类型曲线提供了到NURBS的转换器。此处的统一对于几何引擎的吸引力在于各种算法可以提供统一接口