机器学习中的逻辑回归Logistic Regression
假设数据服从 u=0, s=1 的逻辑斯蒂分布
logistic回归为什么要使用sigmoid函数
Logistic Function
逻辑回归(Logistic Regression)的名称是由其使用的核心函数–Logistic function得来的。
Logistic函数也叫作Sigmoid函数,最初由统计学家发明用来描述生态学中人口增长的特点。起初阶段大致是指数增长然后随着接近环境容量开始变得饱和,增加变慢;最后,达到成熟时增加停止。
Logistic 函数曲线是S型,能将任何实数映射到0~1之间,但又无法达到其极限。
Representation Used for Logistic Regression
Logistic regression的公式表达出来很像线性回归。
逻辑回归与线性回归的关键不同在于:线性回归的输出值为二元值(0、1)而不是概率数值。
将输入变量(x)与权重(weights)或偏差系数(
β
β
)线性结合来预测输出值(y)
其中 wT w T 是单一输入变量x的权重系数,b是噪音系数。你输入数据的每一列都有一个相关联的实数常量系数b,其由训练学习而来。
Logistic Regression损失函数
假设有m组训练样本
(x(1),y(1)),...,(x(m),y(m))
(
x
(
1
)
,
y
(
1
)
)
,
.
.
.
,
(
x
(
m
)
,
y
(
m
)
)
,你需要训练你模型的参数使
y^(i)≈y(i)
y
^
(
i
)
≈
y
(
i
)
Loss(error) function:
Why not 为什么不使用误差平方和来作为代价函数:
这时候的代价函数是非凸的,也就是函数图像中会出现许多的局部最小值,导致梯度下降法极其容易得到局部最小值。如下:
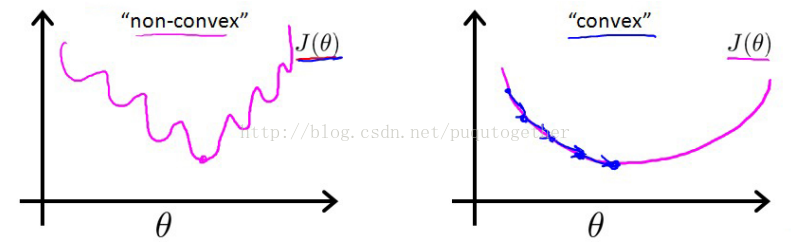
Cost function:
Sigmod函数求导
逻辑回归中我们的目标就是最小化损失函数 J(θ) J ( θ )
令 y^=hθ(x) y ^ = h θ ( x )

Logistic回归优缺点:
优点:实现简单,易于理解和实现;计算代价不高,速度很快,存储资源低;
缺点:容易欠拟合,分类精度可能不高
正则化的Logistic Regression
logistic回归通过正则化(regularization)惩罚参数,防止其取得过大,可以避免过拟合问题(overfitting),其代价函数如下:
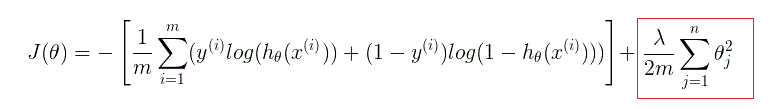
References:
[1] https://www.coursera.org/learn/neural-networks-deep-learning/lecture/5sdh6/logistic-regression-gradient-descent
[2] [Machine Learning & Algorithm]CAML机器学习系列1:深入浅出ML之Regression家族








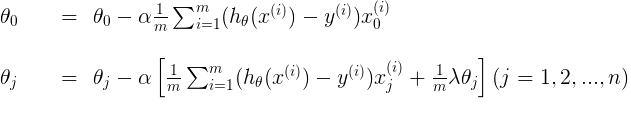














 858
858

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








