隐马尔模型----四

前言

　　到目前为止，马尔科夫模型的三个基本问题中只剩下最后一个问题：预测问题，还没有解决。本节我们将介绍马尔科夫模型预测的两种算法：近似算法与维特比算法（Viterbi Algorithm）

近似算法

　　近似算法的思想是，在每个时刻t选择在该时刻最有可能出现的状态，从而得到一个状态序列，将它作为预测的结果。
　　给定隐马尔科夫模型和观测序列O,在时刻t处于状态的概率为
　　

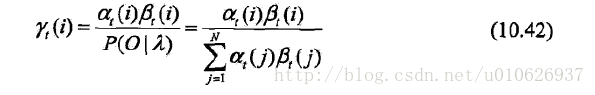
在每一个时刻t最有可能的状态 是

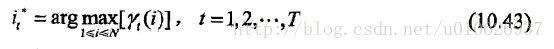
从而得到一个状态序列 ，将它作为预测的结果。

　　近似算法的优点是计算简单，其缺点是不能保证预测的状态序列整体上是最有可能的状态序列，因为预测的状态序列可能有实际不发生的部分，事实上，上述方法得到的状态序列中有可能存在转移概率为0的相邻状态，即对某些i,j ,aij=0时。尽管如此，近似算法仍然是有用的。

维特比算法

维特比算法实际上是用动态规划解隐马尔可夫模型的预测问题，即用动态规划（Dynamic programming）求最大路径（最优路径）算法。这时一条路径对应着一个状态序列。

　　根据动态规划原理，最优路径具有这样的特性：如果最优路径在时刻t通过结点，那么这一路径从结点到终点的部分路径，对于从到的所有可能的部分路径来说，必须是最优的。因为假如不是这样，那么从到就有另一条更好的部分路径存在，如果把它和从到达的部分路径链接起来，就会形成一条比原来的路径更优的路径，这是矛盾的。依据这一原理，我们只需从时刻t=1开始，递推地计算在时刻t状态为i的各条部分路径的最大概率，直至得到时刻t=T状态为i的各条路径的最大概率，时刻t=T的最大概率即为最优路径的概率，最优路径的终结点也同时得打。之后，为了找出最优路径的各个结点，从终结点开始，由后向前逐步求得结点，得到最优路径。这就是维特比算法。

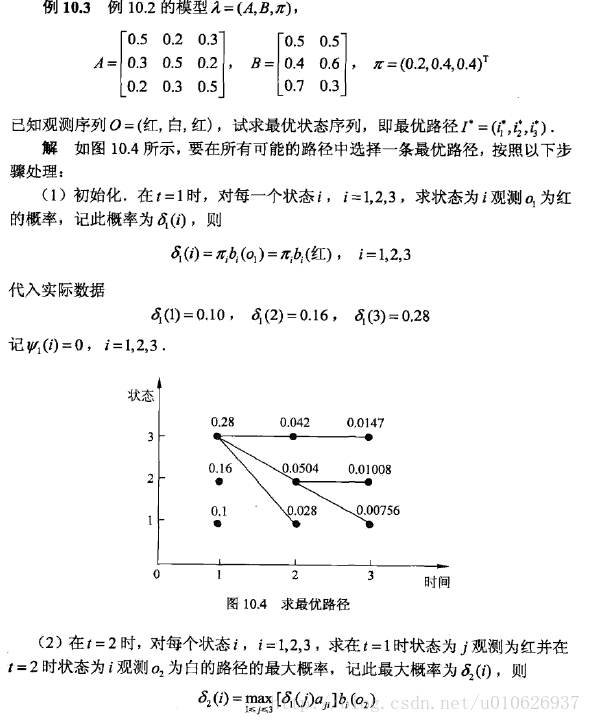
例子讲解

本节完

所谓的不平凡就是平凡的N次幂！