Tutte’s embedding
原理:如果边界顶点有序的落在一个凸多边形上,且内部的顶点是其邻居的线性组合,那么(u,v)坐标参数化是双射的。
[ 1 0 0 0 ⋯ 0 1 0 0 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ w i , 0 w i , 1 − Σ w i , j w i , 4 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ] [ u 0 v 0 u 1 v 1 u 2 v 2 u 3 v 3 u 4 v 4 ] = [ u 0 B o u n d v 0 B o u n d u 1 B o u n d v 1 B o u n d 0 0 0 0 0 0 ] \begin{bmatrix} 1&0&0&0&\cdots \\ 0&1&0&0&\cdots\\ \cdots & \cdots & \cdots & \cdots & \cdots\\ w_{i,0}&w_{i,1}&-\Sigma w_{i,j}&w_{i,4} & \cdots\\ \cdots & \cdots & \cdots & \cdots & \cdots \end{bmatrix}\begin{bmatrix}u0&v0\\ u1&v1\\u2&v2\\u3&v3\\u4&v4\\\end{bmatrix}=\begin{bmatrix}u0Bound&v0Bound\\ u1Bound&v1Bound\\0&0\\0&0\\0&0\\\end{bmatrix} ⎣⎢⎢⎢⎢⎡10⋯wi,0⋯01⋯wi,1⋯00⋯−Σwi,j⋯00⋯wi,4⋯⋯⋯⋯⋯⋯⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡u0u1u2u3u4v0v1v2v3v4⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡u0Boundu1Bound000v0Boundv1Bound000⎦⎥⎥⎥⎥⎤
对于边界上的点,uv的值已知,对于内部的点,其和邻居的线性组合为0。
当边ij存在时,
w
i
j
w_{ij}
wij不为0,反之,
w
i
j
w_{ij}
wij为0。
w
i
j
w_{ij}
wij有许多种取值方法:
1.
u
n
i
f
o
r
m
w
i
j
=
1
1.uniform\space w_{ij}=1
1.uniform wij=1
2.
e
d
g
e
−
b
a
s
e
d
w
i
j
=
1
∣
∣
v
i
−
v
j
∣
∣
2.edge-based\space w_{ij}=\frac{1}{||v_{i}-v_{j}||}
2.edge−based wij=∣∣vi−vj∣∣1
3.
h
a
r
m
o
n
i
c
w
i
j
=
c
o
t
α
i
j
+
β
i
j
2
3.harmonic\space w_{ij}=\frac{cot\alpha_{ij}+\beta_{ij}}{2}
3.harmonic wij=2cotαij+βij
4.
m
e
a
n
−
v
a
l
u
e
w
i
j
=
t
a
n
(
γ
i
j
)
+
t
a
n
(
δ
i
j
)
2
∣
∣
v
i
−
v
j
∣
∣
4.mean-value\space w_{ij}=\frac{tan(\gamma_{ij})+tan(\delta_{ij})}{2||v_{i}-v_{j}||}
4.mean−value wij=2∣∣vi−vj∣∣tan(γij)+tan(δij)
代码步骤:
1.找出边界
2.把边界映射到二维的圆上
3.计算矩阵L
3.1若该点为边界点,跳过
3.2若该点不是边界点,计算权重
3.3将所有的边界点
L
(
i
,
i
)
L(i,i)
L(i,i)的值设为0
4.求解方程组
4.1求解
L
u
=
b
u
Lu=b_{u}
Lu=bu
4.2求解
L
v
=
b
v
Lv=b_{v}
Lv=bv
对于步骤1:
1.要考虑有多个边界的情况:
1.1找出所有边界点
1.2将边界点归类到各自的边界中
1.3以最长的边界作为结果
#include "tutte.h"
#include "map_vertices_to_circle.h"
#include "boundary_loop.h"
#include "cotmatrix.h"
void tutte(
const Eigen::MatrixXd & V,
const Eigen::MatrixXi & F,
Eigen::MatrixXd & U)
{
Eigen::VectorXi boundary;
cgpl::boundary_loop(F, boundary);
Eigen::MatrixXd UV;
cgpl::map_vertices_to_circle(V, boundary, UV);
std::vector<bool> isBound(V.rows(), false);
for (int i = 0; i < boundary.rows(); i++)
{
isBound[boundary(i, 0)] = true;
}
Eigen::SparseMatrix<double> L;
typedef Eigen::Triplet<double> T;
std::vector<T> tripletList;
for (int f = 0; f < F.rows(); f++) {
for (int i = 0; i < 3; i++) {
int ii = F(f, i);
if (isBound[ii])
{
continue;
}
int j = (i + 1) % 3;
int k = (i + 2) % 3;
double norm_ij = (V.row(F(f, i)) - V.row(F(f, j))).norm();
double norm_ik = (V.row(F(f, i)) - V.row(F(f, k))).norm();
// case i != j
tripletList.push_back(T(F(f, i), F(f, j), 1.0/norm_ij));
tripletList.push_back(T(F(f, i), F(f, k), 1.0/norm_ik));
// case i == j
tripletList.push_back(T(F(f, i), F(f, i), -1.0/norm_ij));
tripletList.push_back(T(F(f, i), F(f, i), -1.0/norm_ik));
}
}
for (int i = 0; i < boundary.rows(); i++)
{
tripletList.push_back(T(boundary(i), boundary(i), 1));
}
L.resize(V.rows(), V.rows());
L.setFromTriplets(tripletList.begin(), tripletList.end());
U.resize(V.rows(), 2);
Eigen::SparseLU<Eigen::SparseMatrix<double>, Eigen::COLAMDOrdering<int>>solver;
Eigen::VectorXd Bu = Eigen::VectorXd::Zero(V.rows());
Eigen::VectorXd Bv = Eigen::VectorXd::Zero(V.rows());
for (int i = 0; i < boundary.rows(); i++)
{
Bu(boundary[i]) = UV(i, 0);
Bv(boundary[i]) = UV(i, 1);
}
solver.compute(L);
Eigen::VectorXd u=solver.solve(Bu);
Eigen::VectorXd v=solver.solve(Bv);
U << u, v;
}
#include "boundary_loop.h"
#include "triangle_triangle_adjacency.h"
#include "vertex_triangle_adjacency.h"
#include "is_border_vertex.h"
#include <set>
void cgpl::boundary_loop(
const Eigen::MatrixXi & F,
std::vector<std::vector<int> >& L)
{
using namespace std;
using namespace Eigen;
if(F.rows() == 0)
return;
MatrixXi TT;
vector<std::vector<int>> VF, VFi;
triangle_triangle_adjacency(F,TT);
vertex_triangle_adjacency(F.maxCoeff()+1,F,VF,VFi);
vector<bool> unvisited = is_border_vertex(F);
set<int> unseen;
for (size_t i = 0; i < unvisited.size(); ++i)
{
if (unvisited[i])
unseen.insert(unseen.end(),i);
}
while (!unseen.empty())
{
vector<int> l;
// Get first vertex of loop
int start = *unseen.begin();
unseen.erase(unseen.begin());
unvisited[start] = false;
l.push_back(start);
bool done = false;
while (!done)
{
// Find next vertex
bool newBndEdge = false;
int v = l[l.size()-1];
int next;
for (int i = 0; i < (int)VF[v].size() && !newBndEdge; i++)
{
int fid = VF[v][i];
if (TT.row(fid).minCoeff() < 0.) // Face contains boundary edge
{
int vLoc = -1;
if (F(fid,0) == v) vLoc = 0;
if (F(fid,1) == v) vLoc = 1;
if (F(fid,2) == v) vLoc = 2;
int vNext = F(fid,(vLoc + 1) % F.cols());
newBndEdge = false;
if (unvisited[vNext] && TT(fid,vLoc) < 0)
{
next = vNext;
newBndEdge = true;
}
}
}
if (newBndEdge)
{
l.push_back(next);
unseen.erase(next);
unvisited[next] = false;
}
else
done = true;
}
L.push_back(l);
}
}
void cgpl::boundary_loop(
const Eigen::MatrixXi & F,
std::vector<int> & L)
{
using namespace Eigen;
using namespace std;
if(F.rows() == 0)
return;
vector<vector<int> > Lall;
boundary_loop(F,Lall);
int idxMax = -1;
size_t maxLen = 0;
for (size_t i = 0; i < Lall.size(); ++i)
{
if (Lall[i].size() > maxLen)
{
maxLen = Lall[i].size();
idxMax = i;
}
}
//Check for meshes without boundary
if (idxMax == -1)
{
L.clear();
return;
}
L.resize(Lall[idxMax].size());
for (size_t i = 0; i < Lall[idxMax].size(); ++i)
{
L[i] = Lall[idxMax][i];
}
}
void cgpl::boundary_loop(
const Eigen::MatrixXi & F,
Eigen::VectorXi & L)
{
using namespace Eigen;
using namespace std;
if(F.rows() == 0)
return;
vector<int> Lvec;
boundary_loop(F,Lvec);
L.resize(Lvec.size());
for (size_t i = 0; i < Lvec.size(); ++i)
L(i) = Lvec[i];
}
Least Squares Conformal Mappings
原理:尽量保角和保面积
保角
J t = [ ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y ] = [ a − b b a ] = s [ c o s θ − s i n θ s i n θ c o s θ ] J_{t}=\begin{bmatrix} \frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}\\\frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}\end{bmatrix}=\begin{bmatrix}a&-b\\b&a\end{bmatrix}=s \begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\end{bmatrix} Jt=[∂x∂u∂x∂v∂y∂u∂y∂v]=[ab−ba]=s[cosθsinθ−sinθcosθ]
得出:
∂ u ∂ x = ∂ v ∂ y ∂ u ∂ y = − ∂ v ∂ x \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\space \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} ∂x∂u=∂y∂v ∂y∂u=−∂x∂v
▽ u = ▽ v ⊥ \triangledown u=\triangledown v^{\perp} ▽u=▽v⊥
即:
m i n u , v 1 2 ∫ S ∣ ∣ ▽ u − ▽ v ⊥ ∣ ∣ 2 d A min_{u,v}\frac{1}{2}\int_{S}||\triangledown u-\triangledown v^{\perp}||^{2}dA minu,v21∫S∣∣▽u−▽v⊥∣∣2dA
m i n u , v ∫ S ( 1 2 ∣ ∣ ▽ u ∣ ∣ 2 + 1 2 ∣ ∣ ▽ v ∣ ∣ 2 − ▽ u ⋅ ▽ v ⊥ ) d A min_{u,v}\int_{S}(\frac{1}{2}||\triangledown u||^{2}+\frac{1}{2}||\triangledown v||^{2}-\triangledown u \cdot \triangledown v^{\perp})dA minu,v∫S(21∣∣▽u∣∣2+21∣∣▽v∣∣2−▽u⋅▽v⊥)dA
m i n U U T ( [ L L ] − A ) U min_{U}U^{T}(\begin{bmatrix}L&\\ &L\end{bmatrix}-A)U minUUT([LL]−A)U
L是laplacian matrix,A是vector area,把L放在对角线上(专业术语叫啥忘记了)可以只用一次就可计算出u和v的值。
d e t J t = 1 detJ_{t}=1 detJt=1
U T ( [ M M ] ) U = 1 U^{T}(\begin{bmatrix}M&\\ &M\end{bmatrix})U=1 UT([MM])U=1
求解
m i n v 1 2 v T A v s u b j e c t t o v T B v = 1 min_{v}\frac{1}{2} v^{T} Av \space subject\space to\space v^{T} Bv= 1 minv21vTAv subject to vTBv=1
用拉格朗日乘数法把它转化成广义特征值问题
1 2 v T A v + λ ( 1 − v T B v ) \frac{1}{2} v^{T} Av +\lambda(1- v^{T} Bv) 21vTAv+λ(1−vTBv)
A v − λ B v = 0 Av-\lambda Bv=0 Av−λBv=0
A v = λ B v Av=\lambda Bv Av=λBv
1 − v T B v = 0 1- v^{T} Bv=0 1−vTBv=0
v T B v = 1 v^{T} Bv=1 vTBv=1
结果中前两个为平凡解,所以我们取第三个作为结果
#include "lscm.h"
#include "vector_area_matrix.h"
#include <Eigen/SVD>
#include "eigs.h"
#include "repdiag.h"
#include "cotmatrix.h"
#include "massmatrix.h"
void lscm(
const Eigen::MatrixXd & V,
const Eigen::MatrixXi & F,
Eigen::MatrixXd & U)
{
// Solve optimization as a generalized Eigen value problem
// min_U U'QU subject to U'BU = 1
int n = V.rows();
// Compute Q & B
Eigen::SparseMatrix<double> A, L, Q;
cgpl::cotmatrix(V, F, L);
cgpl::repdiag(L, 2, Q);
vector_area_matrix(F, A);
Q = Q - A;
Eigen::SparseMatrix<double> M, B;
cgpl::massmatrix(V, F, M);
cgpl::repdiag(M, 2, B);
// Solve
Eigen::MatrixXd sU;
Eigen::VectorXd sS;
cgpl::eigs(Q, B, 4, sU, sS);
// Somehow, first 2 eigen value ~e^{-13}
// 3, 4, ... looks more reasonable
U.resize(n, 2);
U << sU.col(2).topRows(n), sU.col(2).bottomRows(n);
}
结果
Tutte’s embedding
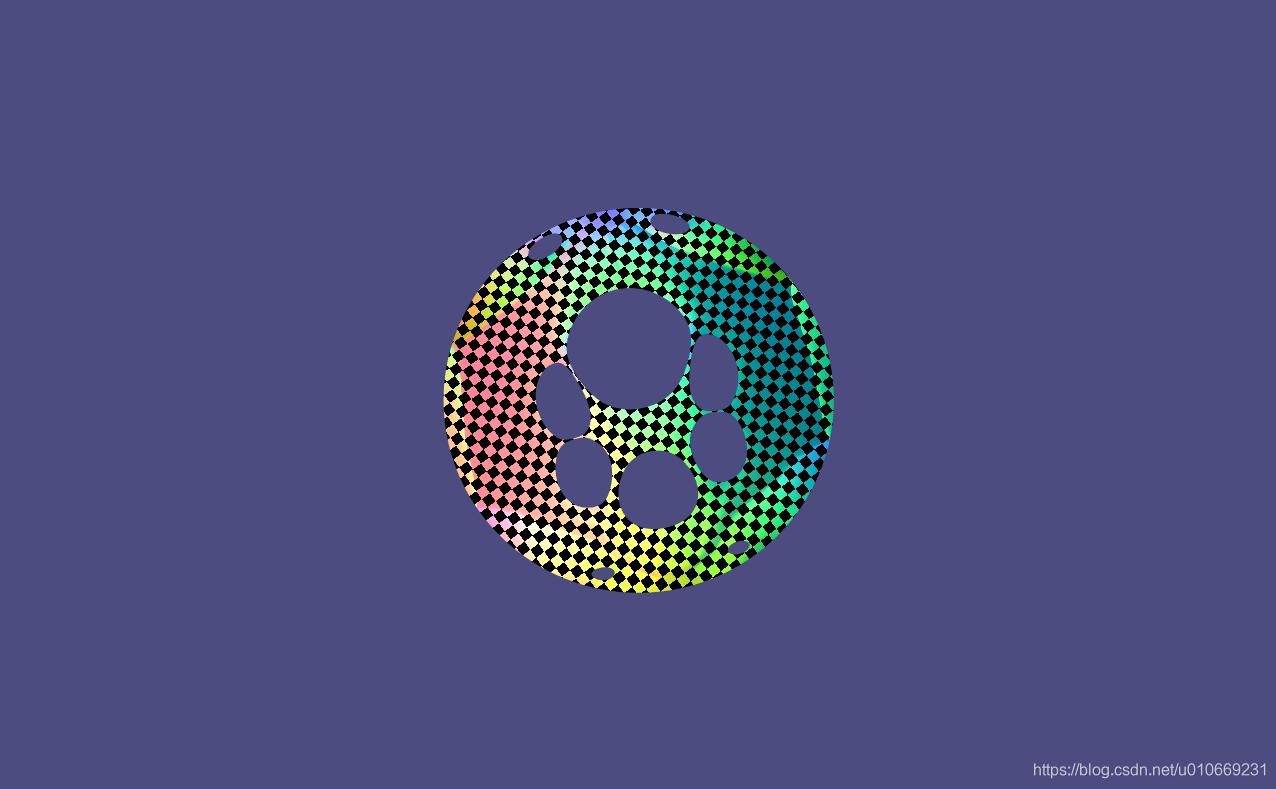

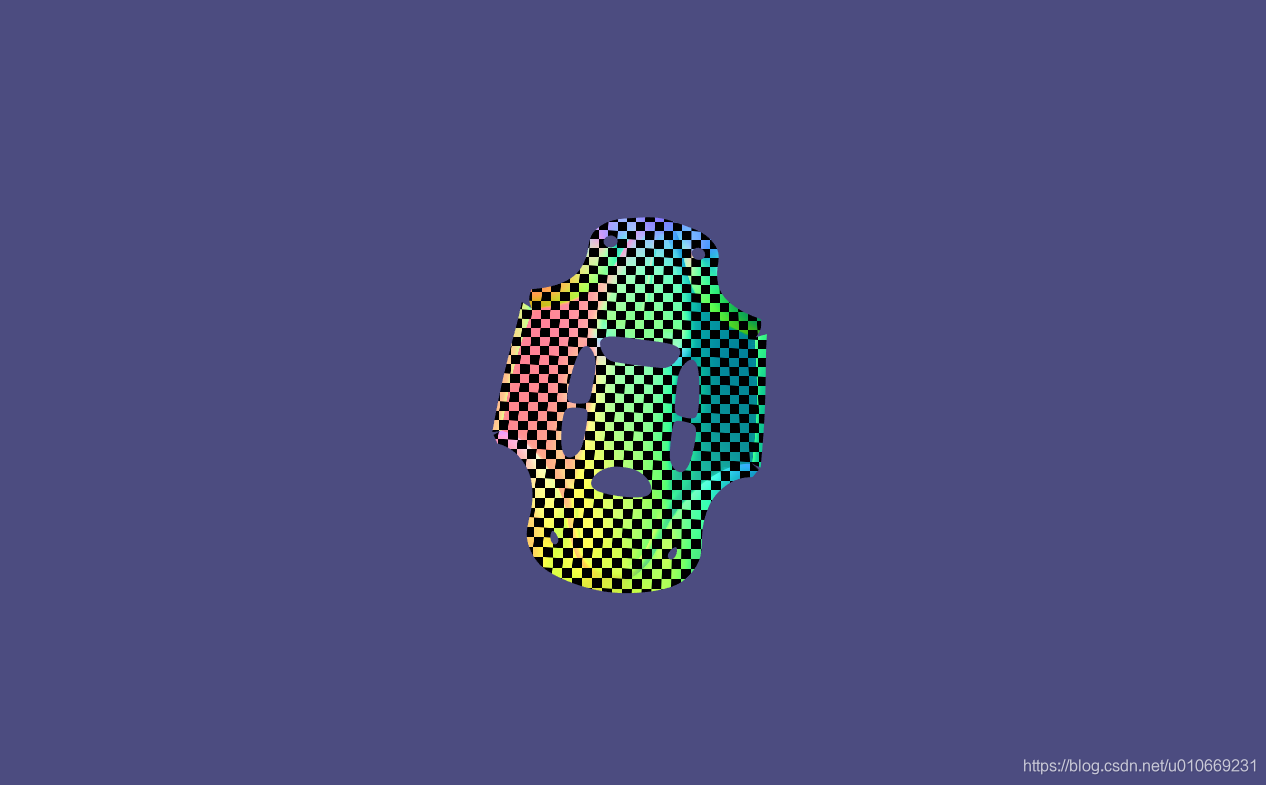
Least Squares Conformal Mappings























 733
733











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








