信号界天王
傅里叶
先生
Jean Baptiste Joseph Fourier
看着好像圈圈。 = =
任意的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式,而正弦函数在物理上是被充分研究而相对简单的函数类,这一想法跟化学上的原子论想法何其相似!
Discrete Fourier Transform,缩写为DFT
是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其DTFT的频域采样。
DFT就是先将信号在时域离散化,求其连续傅里叶变换后,再在频域离散化的结果。
说到傅里叶变换。。当然要知晓采样定理了。
采样定理(又称取样定理、抽样定理)是采样带限信号过程所遵循的规律,1928年由美国电信工程师H.奈奎斯特首先提出来的,因此称为奈奎斯特采样定理。
喜欢科普一下。。
什么是压缩感知,为什么在这里提到他。
压缩感知或压缩传感(Compressive Sensing(CS) or Compressed Sensing、Compressed Sampling)。该理论指出:对可压缩的信号可通过远低于Nyquist标准的方式进行采样数据,仍能够精确地恢复出原始信号。
美国科技评论 评CS为2007年度十大科技进展。
值得一提是 前沿有个华裔帅哥哦
华裔科学家T. Tao
附上 科普文章吧
http://songshuhui.net/archives/11006
现在这个研究很热哦,有打算凑热闹的一起来学习一下哎。。
【7】discrete_fourier_transform
OpenCV2.3.1\opencv\samples\cpp\tutorial_code\core\discrete_fourier_transform
》》》》1
将图像延扩到最佳尺寸.
离散傅立叶变换的运行速度与图片的尺寸息息相关。
当图像的尺寸是2, 3,5的整数倍时,计算速度最快。
(话说。。如果用FFT的话。。应该是2 4 8……吧 为什么是2 3 5 。。。)
通过添凑新的边缘像素的方法获取最佳图像尺寸。
函数 getOptimalDFTSize() 返回最佳尺寸,而函数 copyMakeBorder() 填充边缘像素:
Mat padded; //将输入图像延扩到最佳的尺寸
int m = getOptimalDFTSize( I.rows );
int n = getOptimalDFTSize( I.cols ); // 在边缘添加0
copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));
添加的像素初始化为0.
》》》》2
为傅立叶变换的结果(实部和虚部)分配存储空间.
傅立叶变换的结果是复数,
这就是说对于每个原图像值,结果是两个图像值。 (实部和虚部)
此外,频域值范围远远超过空间值范围, 因此至少要将频域储存在 float 格式中。
结果我们将输入图像转换成浮点类型,并多加一个额外通道来储存复数部分:
Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
Mat complexI;
merge(planes, 2, complexI); // 为延扩后的图像增添一个初始化为0的通道
》》》》3
进行离散傅立叶变换.
支持图像原地计算 (输入输出为同一图像):
dft(complexI, complexI); // 变换结果很好的保存在原始矩阵中
》》》》4
将复数转换为幅度.并且进行 对数尺度(logarithmic scale)缩放.
复数包含实数部分(Re)和复数部分 (imaginary - Im)。
离散傅立叶变换的结果是复数,对应的幅度可以表示为:
傅立叶变换的幅度值范围大到不适合在屏幕上显示。高值在屏幕上显示为白点,而低值为黑点,高低值的变化无法有效分辨。为了在屏幕上凸显出高低变化的连续性,我们可以用对数尺度来替换线性尺度:
// compute the magnitude and switch to logarithmic scale
// => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
split(complexI, planes); // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude
Mat magI = planes[0];
magI += Scalar::all(1); // switch to logarithmic scale
log(magI, magI);
》》》》5
剪切和重分布幅度图象限.
还记得我们在第一步时延扩了图像吗? 那现在是时候将新添加的像素剔除了。
为了方便显示,我们也可以重新分布幅度图象限位置
(注:将第五步得到的幅度图从中间划开得到四张1/4子图像,将每张子图像看成幅度图的一个象限,重新分布即将四个角点重叠到图片中心)。
这样的话原点(0,0)就位移到图像中心。
》》》》6
归一化.
这一步的目的仍然是为了显示。
现在我们有了重分布后的幅度图,但是幅度值仍然超过可显示范围[0,1] 。
我们使用 normalize() 函数将幅度归一化到可显示范围。
normalize(magI, magI, 0, 1, CV_MINMAX);
// 将float类型的矩阵转换到可显示图像范围 (float [0, 1]).
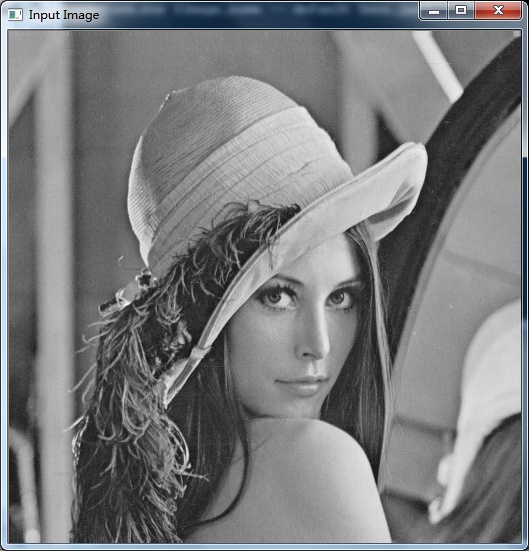
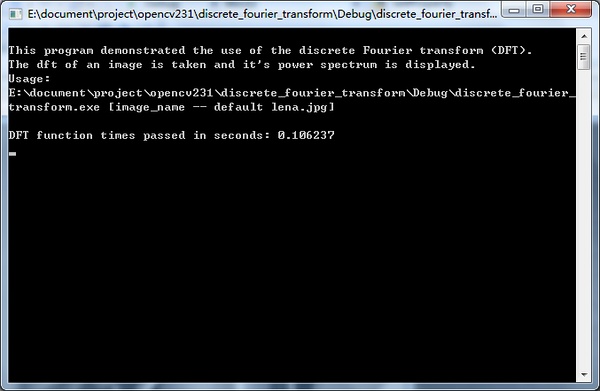
lena姐又来啦
可以看出、、DFT速度还是灰常快哟。要是自己写的话就 = =
补充一下 = =
图像傅立叶变换的物理意义
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。
傅立叶变换的物理意义是
将图像的灰度分布函数变换为图像的频率分布函数,
傅立叶逆变换是将图像的频率分布函数变换为 灰度分布函数
傅立叶变换以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由z=f(x,y)来 表示。
由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维空间中的对应关系。
为什么要提梯度?
因为实际上对图像进行二维傅立叶变换得到频谱图,
就是图像梯度的分布图,
当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在 不移频的情况下也是没有。
傅立叶频谱图上我们看到的明暗不一的亮点,
实际上图像上某一点与邻域点差异的强弱,
即梯度的大小,
也即该点的频率的大小(可以这 么理解,图像中的低频部分指低梯度的点,高频部分相反)。
一般来讲,梯度大则该点的亮度强,否则该点亮度弱。
这样通过观察傅立叶变换后的频谱图,也叫功率 图,
我们首先就可以看出,
图像的能量分布,
如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),
反之,如果 频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。
对频谱移频到原点以后,
可以看出图像的频率分布是以原点为圆心,对称 分布的。
将频谱移频到圆心除了可以清晰地看出图像频率分布以外,
还有一个好处,它可以分离出有周期性规律的干扰信号,
比如正弦干扰,
一幅带有正弦干扰的图,
移频到原点的频谱图上可以看出
除了中心以外还存在以某一点为中心,对称分布的亮点集合,
这个集合就是干扰噪音产生的,
这时可以很直观的通过在该位置放置带阻 滤波器消除干扰
另外我还想说明以下几点:
1、图像经过二维傅立叶变换后,其变换系数矩阵表明:
若变换矩阵Fn原点设在中心,其频谱能量集中分布在变换系数短阵的中心附近(图中阴影区)。
若所用的二维傅立叶变换矩阵Fn的原点设在左上角,那么图像信号能量将集中在系数矩阵的四个角上。
这是由二维傅立叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。
2 、变换之后的图像在原点平移之前四角是低频,最亮,平移之后中间部分是低频,最亮,亮度大说明低频的能量大(幅角比较大)










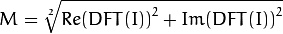
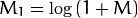















 2130
2130

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








