第一章引子
假设放在你面前有5篮子鸡蛋,每个篮子有且仅有一种蛋,这些蛋表面上一模一样,就是每一种蛋涵盖有且只有一种维生素,分别是A、B、C、D、E。这个时候,你需要估计这五个篮子的鸡蛋的平均重量μ。 首先有个总的假设: 假设每一种维生素的鸡蛋的重量都服从高斯分布。 这个时候,因为每个篮子的鸡蛋包含有且只有一种,并且彼此之间相同的维生素,即每个篮子的鸡蛋都服从相同的分布,这个时候可以用极大似然估计去估计每一种维生素鸡蛋的平均重量。
现在问题来了: 我把那5种鸡蛋混在一起,这个时候要你去估计这5中鸡蛋的平均重量和方差? 仍旧假设:每一种维生素的鸡蛋的重量都服从高斯分布 这个时候有两个参数需要估计均值μ和方差σ。 你从5中鸡蛋里面去拿一种鸡蛋,每种鸡蛋被拿到的概率是呈一定分布的(不一定就是均匀分布,然后概率是1/5)。假设第j中鸡蛋被拿到的概率是φj。
因此你有三个未知量,即隐含量: φj、均值μ和方差σ。
现在是如果你知道类别z(j),你就能根据极大似然估计计算其他两个隐含量。令每个鸡蛋的重量用x(i)表示,x(i)服从高斯分布。 。(x(i)|z(i)=j)~N(μ,σ2)
高斯混合模型(gaussian mixture model-GMM)就是上述问题的抽象模型,即对于每一个样本x(i),先从k个类别中按某种分布抽取一个z(i),然后从这个类别下的高斯分布中生成一个样本x(i)
第二章 GMM数学推导
假设独立样本集是{x(1)......x(m)},这些样本是从k个高斯分布的数据里面抽取出来的。从k不同分布中抽取某一类别是呈某种分布,假设抽取到类别z(i)的概率是p(z(i)=j)= φj。因此这里面会有三个隐含变量: φj、均值μ和方差σ,令这三个变量构成一个集合θ.
则利用极大似然估计θ就是我们非常熟悉的极大似然估计函数:
即:
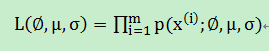
就连乘变成连加,取对数有:
接下来,我们利用EM算法来估计这些参数。EM算法请参看(http://blog.csdn.net/u010866505/article/details/77877345).
1. 先假设我们知道样本的类别z(i),然后计算期望E,即后验概率:
2. 然后就是M-step:
求偏导可以计算均值 μj:
在公式(1)中,如果均值和方差固定的话,那么(1)式可以简化成:
为了计算优化(3)式,而 又满足一定的条件,即 ,如果你知道大名鼎鼎的支持向量机(SVM)的优化目标函数是如何得到的话?这里也就明白了。拉格朗日乘子。构造拉格朗日函数如下:
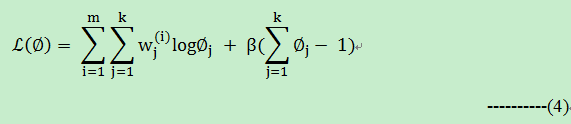
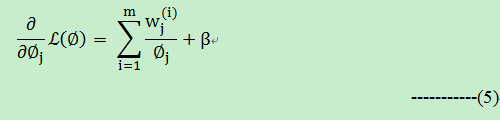
令(5)式=0,计算有:
上面(6)式两边做如下处理:
因此(6)式得到如下变换:
接下来就是计算方差:对(1)公式计算方差 的偏导:
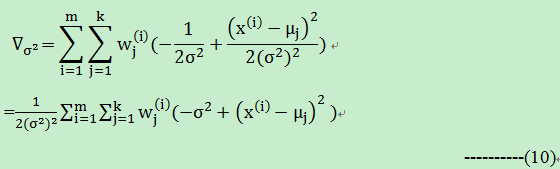
令(10)式等于0,可以计算得到方差的公式如下:
(2)+(8)+(11)就是我们估计参数的最后的解。
第三章 GMM代码-python实现
如下是GMM算法的简单实现,
#! /usr/bin/env python
#! -*- coding=utf-8 -*-
#模拟两个正态分布的参数
from numpy import *
import numpy as np
import random
import copy
SIGMA = 6
EPS = 0.0001
#均值不同的样本
def generate_data():
Miu1 = 2
Miu2 = 4
sigma1 = 1
sigma2 = 2
alpha1 = 0.4
alpha2 = 0.6
N = 5000
N1 = int(alpha1 * N)
X = mat(zeros((N,1)))
for i in range(N1):
temp = random.uniform(0,0.5)
X[i] = temp * sigma1 + Miu1
for i in range(N-N1):
temp = random.uniform(0,0.5)
X[i+N1] = temp * sigma2 + Miu2
return X
#EM算法
def my_GMM(X):
k = 2
N = len(X)
Miu = np.random.rand(k,1)
Posterior = mat(zeros((N,k)))
sigma = np.random.rand(k,1)
sigma[0]=1
#sigma[1]=2
alpha = np.random.rand(k,1)
alpha[0] = 0.1
alpha[1] = 0.9
dominator = 0
numerator = 0
#先求后验概率
print sigma
for it in range(1000):
for i in range(N):
dominator = 0
for j in range(k):
dominator = dominator + np.exp(-1.0/(2.0*sigma[j]) * (X[i] - Miu[j])**2)
#print -1.0/(2.0*sigma[j]),(X[i] - Miu[j])**2,-1.0/(2.0*sigma[j]) * (X[i] - Miu[j])**2,np.exp(-1.0/(2.0*sigma[j]) * (X[i] - Miu[j])**2)
#return
for j in range(k):
numerator = np.exp(-1.0/(2.0*sigma[j]) * (X[i] - Miu[j])**2)
Posterior[i,j] = numerator/dominator
oldMiu = copy.deepcopy(Miu)
oldalpha = copy.deepcopy(alpha)
oldsigma = copy.deepcopy(sigma)
#最大化
for j in range(k):
numerator = 0
dominator = 0
for i in range(N):
numerator = numerator + Posterior[i,j] * X[i]
dominator = dominator + Posterior[i,j]
Miu[j] = numerator/dominator
alpha[j] = dominator/N
tmp = 0
for i in range(N):
tmp = tmp + Posterior[i,j] * (X[i] - Miu[j])**2
#print tmp,Posterior[i,j],(X[i] - Miu[j])**2
sigma[j] = tmp/dominator
print tmp, dominator, sigma[j]
if ((abs(Miu - oldMiu)).sum() < EPS) and \
((abs(alpha - oldalpha)).sum() < EPS) and \
((abs(sigma - oldsigma)).sum() < EPS):
print Miu,sigma,alpha,it
break
if __name__ == '__main__':
X = generate_data()
my_GMM(X)








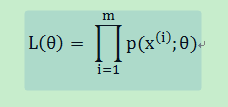

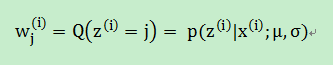
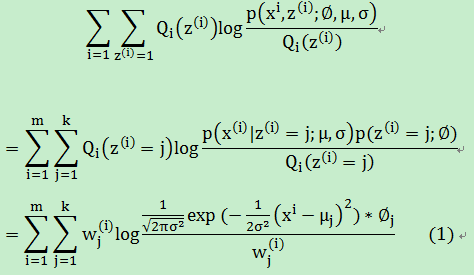


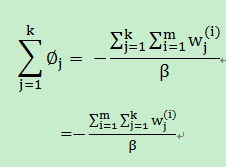


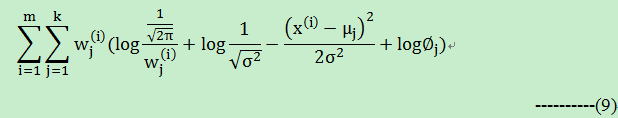
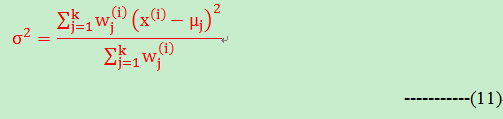














 1313
1313

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








