Week of Code：GG

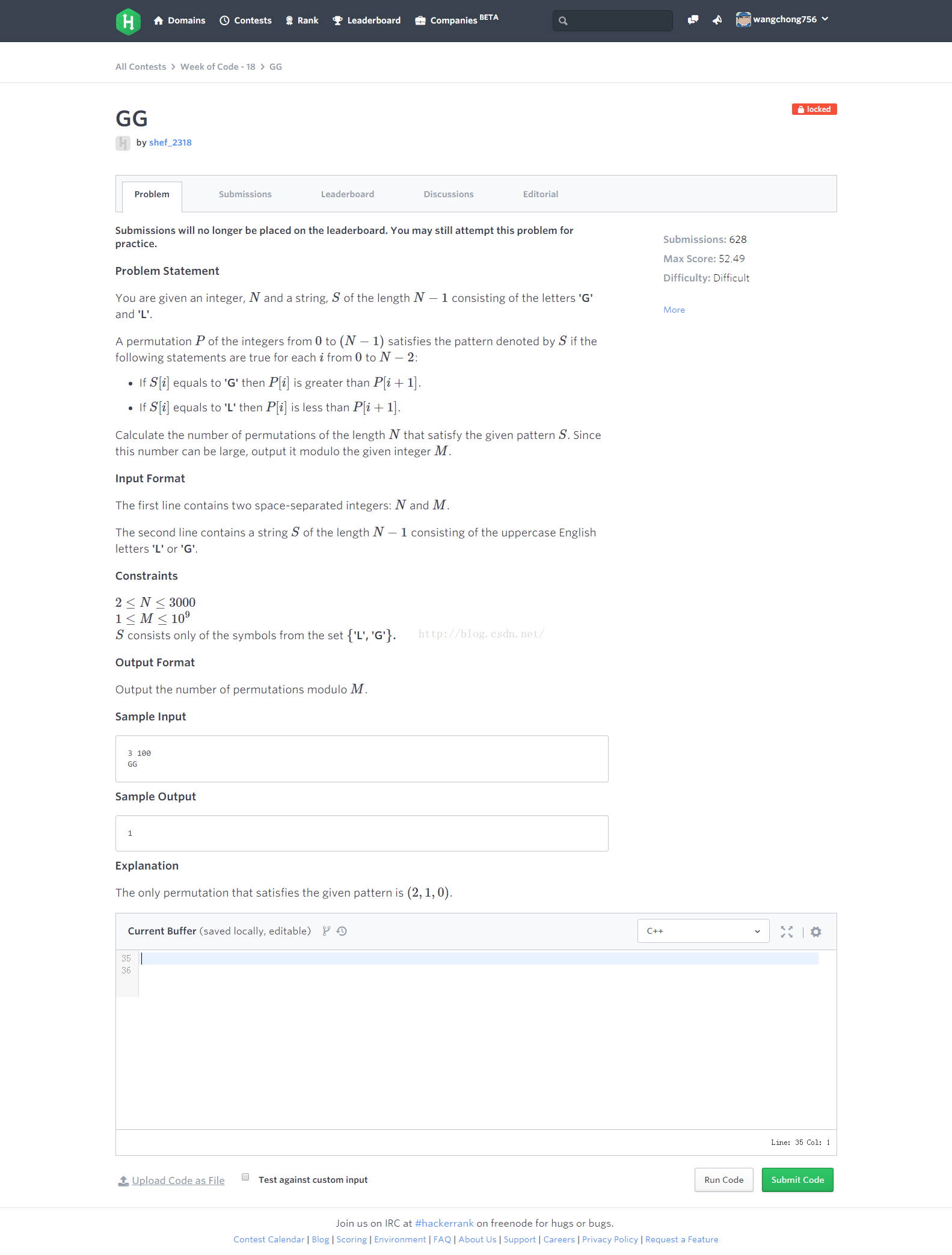
题意是给出一个数n，一个长度为n-1的字符串。求的是1到n符合要求的序列的数量，该序列需要满足当该位置为G时，这个位置的数大于后面位置的数。当该位置为L时，这个位置的数要小于后面位置的数。最后数量模m。

dp[x][y]表示x个数，以x数里面第y小的数结尾的符合要求的数量。

然后如果该位置为G，也就是说新来的数比原来结尾的数要小(注意等于也可以)，那么dp[i+1][k]=sum(dp[i][j])(j>=k)

如果该位置为L，新来的数比原来结尾的数大，那么dp[i+1][k]=sum(dp[i][j])(j<k)。

这个时候这个算法复杂度是O(n^3)。

把复杂度化简成O(n^2)。具体就是发现每一次的dp[i][j]都是以一段一段(.......)的方式往dp[i+1][k]贡献，所以可以通过求前缀和把复杂度降到O(n^2)。

这个题目Topcoder也有类似的，不过那个题目数据量不大，O(n^3)也能过掉。个人觉得这个问题特别绕。。。。又是想了一晚上，最后按照自己的想法终于调出来了。。。太开心了。。。

另外看了编程之美上的对代码的写法问题，要尽量把代码模块化。在51nod上看了一个Google工程师写的一些代码，发现果真如书中所言，写得既简洁又漂亮。那道题同样是暴力，比我什么都在main里面干强多了，好多东西模块化之后思路也都变得清晰了许多。

代码：

#pragma warning(disable:4996)  
#include <iostream>  
#include <algorithm>  
#include <cmath>  
#include <vector>  
#include <string>  
#include <cstring>
#include <queue>
#include <map>
using namespace std;
typedef long long ll;

const int MAXN = 5000 + 5;

int n, mod, dp[MAXN][MAXN], ret;
string s;

void input()
{
	cin >> n >> mod;
	cin >> s;
}

void work()
{
	int i, j;
	dp[1][1] = 1;
	for (i = 1; i < n; i++)
	{
		for (j = 1; j <= i; j++)
		{
			dp[i][j] = (dp[i][j] + dp[i][j - 1]) % mod;
		}
		for (j = 1; j <= i + 1; j++)
		{
			if (s[i - 1] == 'L')
			{
				dp[i + 1][j] = (dp[i + 1][j] + dp[i][j - 1]) % mod;
			}
			else
			{
				dp[i + 1][j] = (dp[i + 1][j] + dp[i][i]) % mod;
				dp[i + 1][j] = (dp[i + 1][j] - dp[i][j - 1] + mod) % mod;
			}
		}
	}
	ret = 0;
	for (i = 1; i <= n; i++)
	{
		ret = (ret + dp[n][i]) % mod;
	}

	cout << ret << endl;
}

int main()
{
	//freopen("i.txt", "r", stdin);
	//freopen("o.txt", "w", stdout);

	input();
	work();

	//system("pause");
	return 0;
}