K-D tree

（感谢CSDN作者zhj5乘风提供的细致入微的解释与百度百科作者nhpcc506）

简介

K-D tree 是K-dimensional tree的简称，是一种用于分割k维数据空间的数据结构。主要应用与多维空间关键数据的搜索（如：范围搜索和最邻近搜索）。K-D tree是二进制空间分割树的特殊情况。

应用

SIFT算法中做特征点匹配时就会用到K-D tree。而特征点匹配实际上就是一个通过距离函数在高维矢量之间进行相似性检索的问题。针对如何快速而准确地找到查询点的近邻，现在提出了很多高维空间索引结构和近似查询的算法，k-d树就是其中一种。

索引结构中相似性查询有两种基本的方式：一种是范围查询（range searches），另一种是K近邻查询（K-neighbor searches）。范围查询就是给定查询点和查询距离的阈值，从数据集中找出所有与查询点距离小于阈值的数据；K近邻查询是给定查询点及正整数K，从数据集中找到距离查询点最近的K个数据，当K=1时，就是最近邻查询（nearest neighbor searches）。

特征匹配算子大致可以分为两类。一类是线性扫描法，即将数据集中的点与查询点逐一进行距离比较，也就是穷举，缺点很明显，就是没有利用数据集本身蕴含的任何结构信息，搜索效率较低，第二类是建立数据索引，然后再进行快速匹配。因为实际数据一般都会呈现出簇状的聚类形态，通过设计有效的索引结构可以大大加快检索的速度。索引树属于第二类，其基本思想就是对搜索空间进行层次划分。根据划分的空间是否有混叠可以分为Clipping和Overlapping两种。前者划分空间没有重叠，其代表就是k-d树；后者划分空间相互有交叠，其代表为R树。

实例

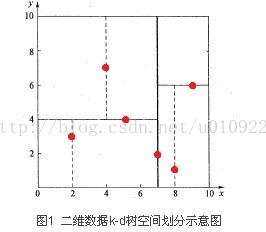
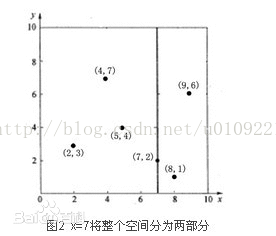
先以一个简单直观的实例来介绍k-d树算法。假设有6个二维数据点{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，数据点位于二维空间内（如图1中红点所示）。k-d树算法就是要确定图1中这些分割空间的分割线（多维空间即为分割平面，一般为超平面）。下面就要通过一步步展示k-d树是如何确定这些分割线的。

k-d树算法可以分为两大部分，一部分是有关k-d树本身这种数据结构建立的算法，另一部分是在建立的k-d树上如何进行最邻近查找的算法。

首先通过一个问题的形式解答：

给定平面上一个点集E，还有一个定点V，怎么在一群点中找出一个点U，使得V与U的距离最近（欧几里得距离）？

枚举法：枚举E中所有的点，找出它们中距离V 最近的点U。

假设现在有两个点集E1与E2，对于E2中每一个点Vi,找出一个在E1 中的一个点Ui，使得 Vi 到 Ui 的距离最短，这样的问题使用枚举法( O(n) 的复杂度 )的代价就太大了。

K-D tree这种数据结构能够较为明显地降低这类问题的复杂度。

K-D tree 是一种二叉树，它能在log(n)（最坏情况是sqrt(n)）的时间复杂度下求出一个点集E中，距离一个定点V最近的点（最邻近查询），通过修改可以求出点集 E 中距离距离 V 最近的 k 个点（k邻近查询）。

为了解决上面的问题将点集 E中的点按照某种规则建成一棵二叉树，查询的时候就在这颗建好的二叉树上面用 log(n) （最坏是 sqrt(n)）的时间复杂度查询出距离最近的点。

各种数据结构之所以能够高效地处理数据，不管是划分树，线段树，字典树，甚至是其他的数据结构或者算法（例如 KMP 之类的）,是因为他们的预处理做得比较好。K-D tree之所以高效，是因为构建树形结构“将点集 E中的点按照某种规则建成一棵二叉树” 的这种规则上。

K：K邻近查询中的k

D：空间是D维空间（Demension）

tree：你可以理解为是二叉树，也可以单纯的看做是一棵 tree。

D维空间制定了一种规则，就是针对空间的“维”。

对于树而言，先指定节点的状态：分裂点（split_point）、分裂方式（split_method）、左儿子（left_son）、右儿子（right_son）.

在建树过程，需要依据节点的状态中的：分裂方式（split_method）。

建树依据：

先计算当前区间 [ L , R ] 中（这里的区间是点的序号区间，而不是我们实际上的坐标区间），每个点的坐标的每一维度上的方差，取方差最大的那一维（数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率），设为 d，作为我们的分裂方式（split_method ），把区间中的点按照在 d 上的大小，从小到大排序，取中间的点 sorted_mid 作为当前节点记录的分裂点，然后，再以 [ L , sorted_mid-1 ] 为左子树建树 ， 以 [sorted_mid+1 , R ] 为右子树建树，这样，当前节点的所有状态我们便确定下来了：

              split_point=sorted_mid

               split_method= d

               left_son    =  [ L , sorted_mid-1 ]

               right_son =  [ sorted_mid+1 , R ]

例子：

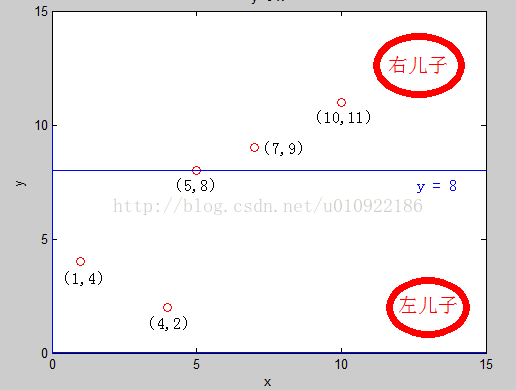
假设现在我们有平面上的点集 E ，其中有 5 个二维平面上的点 ： （1,4）（5,8） （4,2） （7,9） （10，11）。 它们在平面上的分布如图：

首先，我们对区间 [ 1 , 5 ] 建树：

先计算区间中所有点在第一维（也就是 x 坐标）上的方差：

               平均值 ： ave_1 =5.4

               方差 ： varance_1 =9.04

再计算区间中所有点在第二维（也就是 y 坐标）上的方差：

               平均值：ave_2 =6.8

               方差：varance_2 =10.96

明显看见，varance_2 >varance_1 ，那么我们在本次建树中，分裂方式 ：split_method =2 ， 再将所有的点按照 第 2 维 的大小从小到大排序，得到了新的点的一个排列：

（4,2） （1,4）（5,8） （7,9） （10,11）

取中间的点作为分裂点 sorted_mid =（5，8）作为根节点，再把区间 [ 1 , 2] 建成左子树 , [ 4 , 5] 建成右子树，此时，直线 ： y = 8 将平面分裂成了两半，前面一半给左儿子，后面一半给了右儿子，如图：

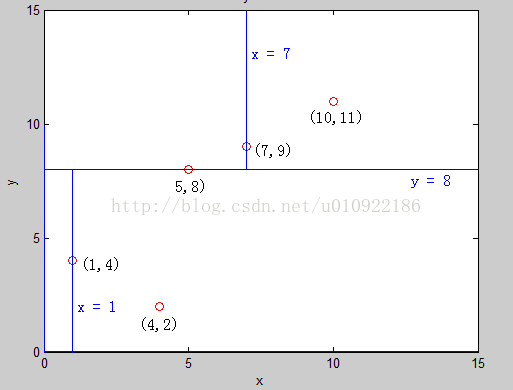
建左子树[1 , 3 ]的时候可以发现，这时候是第一维的方差大，分裂方式就是1，把区间[1, 2]中的点按照第一维的大小，从小到大排序，取中间点（1,4）根节点，再以区间 [2, 2] 建立右子树得到节点（4,2）建右子树 [4,5] 的时候可以发现，这时还是第一维的方差大，于是，我们便得到了这样的一颗二叉树也就是 K-D tree，它把平面分成了如下的小平面，使得每个小平面中最多有一个点：

可以看见，我们实际上在建树的过程中，把整个平面分成了 4 个部分。

上图的树已经构建完成，下面考虑如何查询：

查询过程：

查询，其实相当于我们要将一个点“添加”到已经建好的 K-D tree 中，但并不是真的添加进去，只是找到他应该处于的子空间即可，所以查询就显得简单许多。

每次在一个区间中查询的时候，先看这个区间的分裂方式是什么，也就是说，先看这个区间是按照哪一维来分裂的，这样如果这个点对应的那一维上面的值比根节点的小，就在根节点的左子树上进行查询操作，如果是大的话，就在右子树上进查询操作。

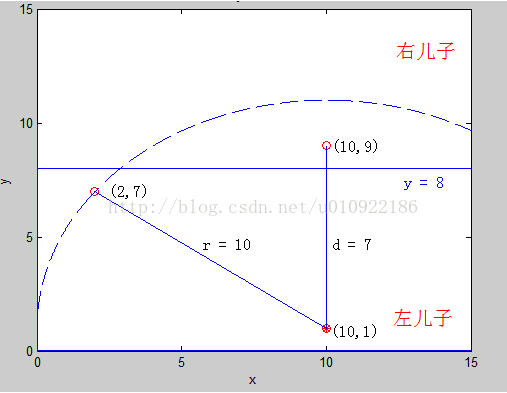
每次回溯到了根节点（也就是说，对他的一个子树的查找已经完成了）的时候，判断一下，以该点为圆心，目前找到的最小距离为半径，看是否和分裂区间的那一维所构成的平面相交，要是相交的话，最近点可能还在另一个子树上，所以还要再查询另一个子树，同时，还要看能否用根节点到该点的距离来更新我们的最近距离。为什么是这样的，我们可以用一幅图来说明：

在查询到左儿子的时候，我们发现，现在最小的距离是 r = 10 ，当回溯到父亲节点的时候，我们发现，以目标点（10,1）为圆心，现在的最小距离 r = 10 为半径做圆，与分割平面 y = 8 相交，这时候，如果我们不在父亲节点的右儿子进行一次查找的话，就会漏掉（10,9）这个点，实际上，这个点才是距离目标点（10,1）最近的点。

每次查询的时候可能会把左右两边的子树都查询完，所以，查询并不是简单的 log(n) 的，最坏的时候能够达到 sqrt(n)。

好了，到此，K-D tree 就差不多了，写法上与很多值得优化的地方，至于怎么把最邻近查询变换到 K 邻近查询，我们用一个数组记录一个点是否可以用来更新最近距离即可，下面贴上 K-D tree 一个模板.

构建k-d树的伪码：

算法：构建k-d树（createKDTree）

输入：数据点集Data-set和其所在的空间Range

输出：Kd，类型为k-d tree

1.If Data-set为空，则返回空的k-d tree

2.调用节点生成程序： （1）确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。以SURF特征为例，描述子为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率； （2）确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set' = Data-set\Node-data（除去其中Node-data这一点）。

3.dataleft = {d属于Data-set' && d[split] ≤ Node-data[split]} Left_Range = {Range && dataleft} dataright = {d属于Data-set' && d[split] > Node-data[split]} Right_Range = {Range && dataright}

4.left = 由（dataleft，Left_Range）建立的k-d tree，即递归调用createKDTree（dataleft，Left_ Range）。并设置left的parent域为Kd； right = 由（dataright，Right_Range）建立的k-d tree，即调用createKDTree（dataright，Right_ Range）。并设置right的parent域为Kd。

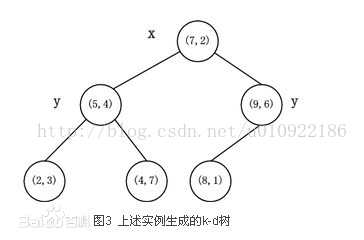
依据上述的方法，可以将可以将图2的数据，构建成图3的树。

在k-d树中进行数据的查找也是特征匹配的重要环节，其目的是检索在k-d树中与查询点距离最近的数据点。这里先以一个简单的实例来描述最邻近查找的基本思路。

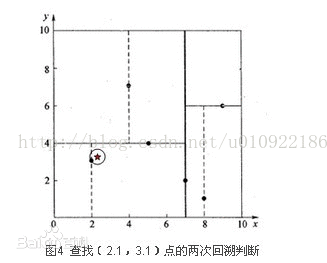
星号表示要查询的点（2.1,3.1）。通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点（2,3）。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行'回溯'操作：算法沿搜索路径反向查找是否有距离查询点更近的数据点。此例中先从（7,2）点开始进行二叉查找，然后到达（5,4），最后到达（2,3），此时搜索路径中的节点为<（7,2），（5,4），（2,3）>，首先以（2,3）作为当前最近邻点，计算其到查询点（2.1,3.1）的距离为0.1414，然后回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如图4所示。发现该圆并不和超平面y = 4交割，因此不用进入（5,4）节点右子空间中去搜索。

再回溯到（7,2），以（2.1,3.1）为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入（7,2）右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点（2,3），最近距离为0.1414。

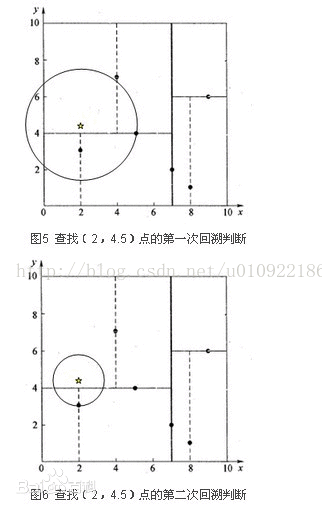
一个复杂点了例子如查找点为（2，4.5）。同样先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，由于查找点为y值为4.5，因此进入右子空间查找到（4,7），形成搜索路径<（7,2），（5,4），（4,7）>，取（4,7）为当前最近邻点，计算其与目标查找点的距离为3.202。然后回溯到（5,4），计算其与查找点之间的距离为3.041。以（2，4.5）为圆心，以3.041为半径作圆，如图5所示。可见该圆和y = 4超平面交割，所以需要进入（5,4）左子空间进行查找。此时需将（2,3）节点加入搜索路径中得<（7,2），（2,3）>。回溯至（2,3）叶子节点，（2,3）距离（2,4.5）比（5,4）要近，所以最近邻点更新为（2，3），最近距离更新为1.5。回溯至（7,2），以（2,4.5）为圆心1.5为半径作圆，并不和x = 7分割超平面交割，如图6所示。至此，搜索路径回溯完。返回最近邻点（2,3），最近距离1.5。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <string>
#include <queue>
#include <stack> 
#define INT_INF 0x3fffffff
#define LL_INF 0x3fffffffffffffff
#define EPS 1e-12
#define MOD 1000000007
#define PI 3.141592653579798
#define N 60000 
using namespace std; 
typedef long long LL;
typedef unsigned long long ULL;
typedef double DB; 
struct data
{
LL pos[10];
int id;
} T[N] , op , point;
int split[N],now,n,demension; 
bool use[N];
LL ans,id;
DB var[10]; 
bool cmp(data a,data b)
{
return a.pos[split[now]]<b.pos[split[now]];
} 
void build(int L,int R)
{
if(L>R) return; 
int mid=(L+R)>>1; 
//求出 每一维 上面的方差
for(int pos=0;pos<demension;pos++)
{
DB ave=var[pos]=0.0;
for(int i=L;i<=R;i++)
ave+=T[i].pos[pos];
ave/=(R-L+1);
for(int i=L;i<=R;i++)
var[pos]+=(T[i].pos[pos]-ave)*(T[i].pos[pos]-ave);
var[pos]/=(R-L+1);
} 
//找到方差最大的那一维，用它来作为当前区间的 split_method
split[now=mid]=0;
for(int i=1;i<demension;i++)
if(var[split[mid]]<var[i]) split[mid]=i; 
//对区间排排序，找到中间点
nth_element(T+L,T+mid,T+R+1,cmp); 
build(L,mid-1);
build(mid+1,R);
} 
void query(int L,int R)
{
if(L>R) return;
int mid=(L+R)>>1; 
//求出目标点 op 到现在的根节点的距离
LL dis=0;
for(int i=0;i<demension;i++)
dis+=(op.pos[i]-T[mid].pos[i])*(op.pos[i]-T[mid].pos[i]); 
//如果当前区间的根节点能够用来更新最近距离，并且 dis 小于已经求得的 ans
if(!use[T[mid].id] && dis<ans)
{
ans=dis; //更新最近距离
point=T[mid]; //更新取得最近距离下的点
id=T[mid].id; //更新取得最近距离的点的 id
} 
//计算 op 到分裂平面的距离
LL radius=(op.pos[split[mid]]-T[mid].pos[split[mid]])* (op.pos[split[mid]]-T[mid].pos[split[mid]]); 
//对子区间进行查询
if(op.pos[split[mid]]<T[mid].pos[split[mid]])
{
query(L,mid-1);
if(radius<=ans) query(mid+1,R);
}
else
{
query(mid+1,R);
if(radius<=ans) query(L,mid-1);
}
} 
int main()
{
while(scanf("%d%d",&n,&demension)!=EOF)
{
//读入 n 个点
for(int i=1;i<=n;i++)
{
for(int j=0;j<demension;j++)
scanf("%I64d",&T[i].pos[j]);
T[i].id=i;
} 
build(1,n); //建树 
int m,q; scanf("%d",&q); // q 个询问
while(q--)
{
memset(use,0,sizeof(use)); 
for(int i=0;i<demension;i++)
scanf("%I64d",&op.pos[i]);
scanf("%d",&m);
printf("the closest %d points are:\n",m);
while(m--)
{
ans=(((LL)INT_INF)*INT_INF);
query(1,n);
for(int i=0;i<demension;i++)
{
printf("%I64d",point.pos[i]);
if(i==demension-1) printf("\n");
else printf(" ");
}
use[id]=1;
}
}
}
return 0;
}