Hessian 矩阵（黑塞矩阵）以及hessian矩阵奇异的用法

Hessian Matrix（黑塞矩阵、海森矩阵、海瑟矩阵、海塞矩阵 etc.）,它是一个多元函数的二阶偏导数构成的方阵，用以描述函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出，并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题。

对于一个实值多元函数  ，如果函数的二阶偏导数都存在，则定义的黑塞矩阵为：

其中表示对第 i 个变量的微分算子，。那么，f 的黑塞矩阵即:

性质：

1. 对称性：

如果函数 f 在D区域内二阶连续可导，那么 f 黑塞函数H(f)在D内为对称方阵。

2. 多元函数极值的判定：

如果实值多元函数 f(x1,x2,...)二阶连续可导，并且在临界点M(xi)（i=1,2,...,n, 且xi已知）处梯度（一阶导数）等于零，即，，M为驻点。仅仅通过一阶导数无法判断在临界点M处是极大值还是极小值。

记

在

点处的黑塞矩阵为

。由于

在

点处连续，所以

是一个

的对称矩阵。对于

，有如下结论：

• 如果H(M)是 正定矩阵，则临界点M处是一个局部的极小值。
• 如果H(M)是 负定矩阵，则临界点M处是一个局部的极大值。
• 如果H(M)是 不定矩阵，则临界点M处不是极值。

提到hessian矩阵奇异，就需要首先介绍一下牛顿法，拟牛顿法，最速下降法。

牛顿法

1、求解方程。

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f'(x0)

求解方程f(x)=0，即f(x0)+(x-x0)*f'(x0)=0，求解x = x1=x0－f(x0)/f'(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f'(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f(x1)的值比f(x0)更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f'(x(n))，通过迭代，这个式子必然在f（x*）=0的时候收敛。整个过程如下图：

2. 牛顿法用于最优化

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

上面的表达式成立的条件是 当且仅当  Δx 无线趋近于0。此时上式等价与：

求解：

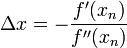
得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

在上面讨论的是2维情况，高维情况的牛顿迭代公式是：