遗传算法与C++实现

最新推荐文章于 2024-09-12 22:22:14 发布

ArthurKingYs

最新推荐文章于 2024-09-12 22:22:14 发布

阅读量2.2k

点赞数

分类专栏：遗传算法文章标签：算法遗传算法 C++

遗传算法专栏收录该内容

7 篇文章 1 订阅

订阅专栏

1、遗传算法，核心是达尔文优胜劣汰适者生存的进化理论的思想。一个种群，通过长时间的繁衍，种群的基因会向着更适应环境的趋势进化，适应性强的个体基因被保留，后代越来越多，适应能力低个体的基因被淘汰，后代越来越少。经过几代的繁衍进化，留下来的少数个体，就是相对能力最强的个体了。

那么在解决一些问题的时候，我们所学习的便是这样的思想。比如先随机创造很多很多的解，然后找一个靠谱的评价体系，去筛选适应性高的解，再用这些适应性高的解衍生出更好的解，然后再筛选，再衍生。反复迭代一定次数，可以得到近似最优解。

2、首先，我们先看看一个经典组合问题：“背包问题”

“背包问题（Knapsack problem）是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。”

这个问题的衍生简化问题 “0-1背包问题” 增加了限制条件：每件物品只有一件，可以选择放或者不放，更适合我们来举例
这样的问题如果数量少，当然最好选择穷举法
比如一共3件商品，用0表示不取，1表示取，那么就一共有
000 001 010
011 100 101
110 111
这样8种方案，然后让计算机去累加和，与重量上限比较，留下来的解里取最大即可。
但如果商品数有300,3000,甚至3w种呢，计算量太大穷举法可能就不适用了，这时如果遗传算法使用得当，就能在较短的时间内帮我们找到近似的最优解，我们继续往下看：
新的问题是12件商品的0-1背包问题
我们先让计算机随机产生1000个12位的二进制数。把总重量超过背包上限的解筛掉，剩下的两两一对随机交换“基因片段”产生下一代
交换前：
0000 1100 1101
0011 0101 0101
交换后：
0000 0101 1101
0011 1100 0101
再筛选，再交配，如此反复几代，留下的“基因型“差不多就是最好的了，如此这般与生物进化规律是一样的。
同时，在生物繁殖过程中，新产生的基因是有一定几率突变的，这是很多优良性状的重要来源，遗传算法中可也不能忽略它

比如：

变异前：

000101100101

变异后：

000101110101

产生突变的位置，就是一个概率问题。在设计算法的时候，会给每个基因位设置一个突变概率（当然是非常了）同样的在基因交换阶段交换哪些基因呢，也是一个算法设置问题。

3、总结一下，遗传算法应该有

一个基本函数：适度函数f(x)
三个基本操作：选择，交叉，变异

一.适度函数
适度函数其实就是指解的筛选标准，比如上文所说的把所有超过上限重量的解筛选掉，但是不是有更好的筛选标准呢？这将直接影响最后结果的接近程度以及求解所耗费的时间，所以设置一个好的适度函数很重要

二.选择
在遗传算法中选择也是个概率问题，在解的范围中适应度更高的基因型有更高的概率被选择到。所以，在选择一些解来产生下一代时，一种常用的选择策略是 “比例选择” ，也就是个体被选中的概率与其适应度函数值成正比。假设群体的个体总数是M，那么那么一个体Xi被选中的概率为f(Xi)/( f(X1) + f(X2) + …….. + f(Xn) )。常用的选择方法――轮盘赌（Roulette Wheel Selection）选择法。

三.交叉
在均等概率下基因位点的交叉，衍生出新的基因型。上述例子中是通过交换两个基因型的部分”基因”，来构造两个子代的基因型。

四.变异
在衍生子代的过程中，新产生的解中的“基因型”会以一定的概率出错，称为变异。变异发生的概率设置为Pm，记住该概率是很小的一个值。因为变异是小概率事件！

五.基本遗传算法优化
为了防止进化过程中产生的最优解被变异和交叉所破坏。《遗传算法原理及应用》介绍的最优保存策略是：即当前种群中适应度最高的个体不参与交叉运算和变异运算，而是用它来替换掉本代群体中经过交叉、变异等遗传操作后所产生的适应度最低的个体。

遗传算法的优点：

1、与问题领域无关且快速随机的全局搜索能力。传统优化算法是从单个初始值迭代求最优解的；容易误入局部最优解。遗传算法从串集开始搜索，复盖面大，利于全局择优。

2、搜索从群体出发，具有潜在的并行性，可以进行多个个体的同时比较，鲁棒性高！

3、搜索使用评价函数启发，过程简单。

4、使用概率机制进行迭代，具有随机性。遗传算法中的选择、交叉和变异都是随机操作，而不是确定的精确规则。这说明遗传算法是采用随机方法进行最优解搜索，选择体现了向最优解迫近，交叉体现了最优解的产生，变异体现了全局最优解的复盖。

5、具有可扩展性，容易与其他算法结合。遗传算法求解时使用特定问题的信息极少，仅仅使用适应值这一信息进行搜索，并不需要问题导数等与问题直接相关的信息。遗传算法只需适应值和串编码等通用信息，故几乎可处理任何问题，容易形成通用算法程序。

6、具有极强的容错能力。遗传算法的初始串集本身就带有大量与最优解甚远的信息；通过选择、交叉、变异操作能迅速排除与最优解相差极大的串；这是一个强烈的滤波过程；并且是一个并行滤波机制。故而，遗传算法有很高的容错能力。

遗传算法具有良好的全局搜索能力，可以快速地将解空间中的全体解搜索出，而不会陷入局部最优解的快速下降陷阱；并且利用它的内在并行性，可以方便地进行分布式计算，加快求解速度。

遗传算法的缺点：

1、遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码

2、三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验

3、没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢，要得要较精确的解需要较多的训练时间

4、算法对初始种群的选择有一定的依赖性（下图所示），能够结合一些启发算法进行改进

5、算法的并行机制的潜在能力没有得到充分的利用，这也是当前遗传算法的一个研究热点方向。

同时，遗传算法的局部搜索能力较差，导致单纯的遗传算法比较费时，在进化后期搜索效率较低。在实际应用中，遗传算法容易产生过早收敛的问题。采用何种选择方法既要使优良个体得以保留，又要维持群体的多样性，一直是遗传算法中较难解决的问题。

-------------------------我------是------分------割--------线------------------------------------------------------------

下面举例来说明遗传算法用以求函数最大值

函数为y = -x²+ 5的最大值，-32<=x<=31

一、编码以及初始种群的产生

编码采用二进制编码，初始种群采用矩阵的形式，每一行表示一个染色体，每一个染色体由若干个基因位组成。关于染色体的长度（即基因位的个数）可根据具体情况而定。比如说根据要求极值的函数的情况，本文-32<=X<=31，该范围内的整数有64个，所以可以取染色体长度为6，（2⁶=64）。综上所述，取染色体长度为6，前5个二进制构成该染色体的值（十进制），第6个表示该染色体的适应度值。若是所取得染色体长度越长，表示解空间搜索范围越大，对应的是待搜索的X范围越大。关于如何将二进制转换为十进制，文后的C代码中函数x即为转换函数。

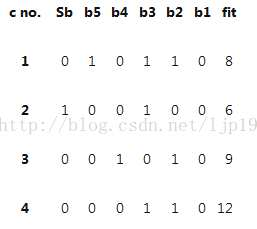
初始种群结构如下图所示：

该初始种群共有4个染色体，第1列表示各个染色体的编号，第2列表示该染色体值的正负号，0表示正，1表示负。第3列到第7列为二进制编码，第8列表示各个染色体的适应度值。第2列到第7列的0-1值都是随机产生的。

二、适应度函数

一般情况下，染色体（也叫个体，或一个解）的适应度函数为目标函数的线性组合。本文直接以目标函数作为适应度函数。即每个染色体的适应度值就是它的目标函数值，f(x)=-x^2+ 5。

三、选择算子

初始种群产生后，要从种群中选出若干个体进行交叉、变异，那么如何选择这些个体呢？选择方法就叫做选择算子。一般有轮盘赌选择法、锦标赛选择法、排序法等。本文采用排序法来选择，即每次选择都选出适应度最高的两个个体。那么执行一次选择操作后，得到的新种群的一部分为下图所示：

四、交叉算子

那么接下来就要对新种群中选出的两个个体进行交叉操作，一般的交叉方法有单点交叉、两点交叉、多点交叉、均匀交叉、融合交叉。方法不同，效果不同。本文采用最简单的单点交叉。交叉点随机产生。但是交叉操作要在一定的概率下进行，这个概率称为交叉率，一般设置为0.5到0.95之间。通过交叉操作，衍生出子代，以补充被淘汰掉的个体。交叉后产生的新个体组成的新种群如下：

黑体字表示子代染色体继承父代个体的基因。

五、变异

变异就是对染色体的基因进行变异，使其改变原来的结构（适应值也就改变），达到突变进化的目的。变异操作也要遵从一定的概率来进行，一般设置为0到0.5之间，即以小概率进行基因突变。这符合自然规律。本文的变异方法直接采取基因位反转变异法，即0变为1，1变为0。要进行变异的基因位的选取也是随机的。

六、终止规则

遗传算法是要一代一代更替的，那么什么时候停止迭代呢？这个规则就叫终止规则。一般常用的终止规则有：若干代后终止，得到的解达到一定目标后终止，计算时间达到一定限度后终止等方法。本文采用迭代数来限制。

代码如下所示：

[cpp] view plain copy

#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream>
typedef struct Chrom // 结构体类型，为单个染色体的结构；
{
short int bit[6];//一共6bit来对染色体进行编码，其中1位为符号位。取值范围-64~+64
int fit ;//适应值
double rfit;//相对的fit值，即所占的百分比
double cfit;//积累概率
}chrom;
//定义将会用到的几个函数；
void *evpop (chrom popcurrent[4]);//进行种群的初始化
int x (chrom popcurrent);
int y (int x);
void *pickchroms (chrom popcurrent[4]);//选择操作
void *pickchroms_new (chrom popcurrent[4]); // 基于概率分布
void *crossover (chrom popnext[4]);//交叉操作
void *mutation (chrom popnext[4]);//突变
double r8_uniform_ab ( double a, double b, int &seed );//生成a~b之间均匀分布的数字
chrom popcurrent [4]; // 初始种群规模为；
chrom popnext [4]; // 更新后种群规模仍为；
void main () // 主函数；
{
int num ; // 迭代次数；
int i ,j, l,Max ,k;
Max=0; // 函数最大值
printf("\nWelcome to the Genetic Algorithm！\n"); //
printf("The Algorithm is based on the function y = -x^2 + 5 to find the maximum value of the function.\n");
enter:printf ("\nPlease enter the no. of iterations\n请输入您要设定的迭代数 : ");
scanf("%d" ,&num); // 输入迭代次数，传送给参数 num；
if(num <1)
goto enter ; // 判断输入的迭代次数是否为负或零，是的话重新输入；
//不同的随机数可能结果不同？？那是当所设置的迭代次数过少时，染色体的基因型过早地陷入局部最优
srand(time(0));
evpop(popcurrent ); // 随机产生初始种群；
//是否需要指定x的取值范围呢？6bit来表示数字，第一位为符号位，5bit表示数字大小。所以，取值范围为-32~+31
Max = popcurrent[0].fit;//对Max值进行初始化
for(i =0;i< num;i ++) // 开始迭代；
{
printf("\ni = %d\n" ,i); // 输出当前迭代次数；
for(j =0;j<4; j++)
{
popnext[j ]=popcurrent[ j]; // 更新种群；
}
pickchroms(popnext ); // 挑选优秀个体；
crossover(popnext ); // 交叉得到新个体；
mutation(popnext ); // 变异得到新个体；
for(j =0;j<4; j++)
{
popcurrent[j ]=popnext[ j]; // 种群更替；
}
} // 等待迭代终止；
//对于真正随机数是需要注意取较大的迭代次数
for(l =0;l<3; l++)
{
if(popcurrent [l]. fit > Max )
{
Max=popcurrent [l]. fit;
k=x(popcurrent [l]);//此时的value即为所求的x值
}
}
printf("\n 当x等于 %d时，函数得到最大值为： %d ",k ,Max);
printf("\nPress any key to end ! " );
flushall(); // 清除所有缓冲区；
getche(); // 从控制台取字符，不以回车为结束；
}
void *evpop (chrom popcurrent[4]) // 函数：随机生成初始种群；
{
int i ,j, value1;
int random ;
double sum=0;
for(j =0;j<4; j++) // 从种群中的第1个染色体到第4个染色体
{
for(i =0;i<6; i++) // 从染色体的第1个基因位到第6个基因位
{
random=rand (); // 产生一个随机值
random=(random %2); // 随机产生0或者1
popcurrent[j ].bit[ i]=random ; // 随机产生染色体上每一个基因位的值，或；
}
value1=x (popcurrent[ j]); // 将二进制换算为十进制，得到一个整数值；
popcurrent[j ].fit= y(value1); // 计算染色体的适应度值
sum = sum + popcurrent[j ].fit;
printf("\n popcurrent[%d]=%d%d%d%d%d%d value=%d fitness = %d",j, popcurrent[j ].bit[5], popcurrent[j ].bit[4], popcurrent[j ].bit[3], popcurrent[j ].bit[2], popcurrent[j ].bit[1], popcurrent[j ].bit[0], value1,popcurrent [j]. fit);
// 输出整条染色体的编码情况，
}
//计算适应值得百分比，该参数是在用轮盘赌选择法时需要用到的
for (j = 0; j < 4; j++)
{
popcurrent[j].rfit = popcurrent[j].fit/sum;
popcurrent[j].cfit = 0;//将其初始化为0
}
return(0);
}
int x (chrom popcurrent) // 函数：将二进制换算为十进制；
{//此处的染色体长度为，其中个表示符号位
int z ;
z=(popcurrent .bit[0]*1)+( popcurrent.bit [1]*2)+(popcurrent. bit[2]*4)+(popcurrent .bit[3]*8)+( popcurrent.bit [4]*16);
if(popcurrent .bit[5]==1) // 考虑到符号；
{
z=z *(-1);
}
return(z );
}
//需要能能够从外部直接传输函数，加强鲁棒性
int y (int x)// 函数：求个体的适应度；
{
int y ;
y=-(x *x)+5; // 目标函数：y= - ( x^ 2 ) +5；
return(y );
}
//基于轮盘赌选择方法，进行基因型的选择
void *pickchroms_new (chrom popnext[4])//计算概率
{
int men;
int i;int j;
double p;
double sum=0.0;
//find the total fitness of the population
for (men = 0; men < 4; men++ )
{
sum = sum + popnext[men].fit;
}
//calculate the relative fitness of each member
for (men = 0; men < 4; men++ )
{
popnext[men].rfit = popnext[men].fit / sum;
}
//calculate the cumulative fitness,即计算积累概率
popcurrent[0].cfit = popcurrent[0].rfit;
for ( men = 1; men < 4; men++)
{
popnext[men].cfit = popnext[men-1].cfit + popnext[men].rfit;
}
for ( i = 0; i < 4; i++ )
{//产生0~1之间的随机数
//p = r8_uniform_ab ( 0, 1, seed );//通过函数生成0~1之间均匀分布的数字
p =rand()%10;//
p = p/10;
if ( p < popnext[0].cfit )
{
popcurrent[i] = popnext[0];
}
else
{
for ( j = 0; j < 4; j++ )
{
if ( popnext[j].cfit <= p && p < popnext[j+1].cfit )
{
popcurrent[i] = popcurrent[j+1];
}
}
}
}
// Overwrite the old population with the new one.
//
for ( i = 0; i < 4; i++ )
{
popnext[i] = popcurrent[i];
}
return(0);
}
void *pickchroms (chrom popnext[4]) // 函数：选择个体；
{
int i ,j;
chrom temp ; // 中间变量
//因此此处设计的是个个体，所以参数是
for(i =0;i<3; i++) // 根据个体适应度来排序；（冒泡法）
{
for(j =0;j<3-i; j++)
{
if(popnext [j+1]. fit>popnext [j]. fit)
{
temp=popnext [j+1];
popnext[j +1]=popnext[ j];
popnext[j ]=temp;
}
}
}
for(i =0;i<4; i++)
{
printf("\nSorting:popnext[%d] fitness=%d" ,i, popnext[i ].fit);
printf("\n" );
}
flushall();/* 清除所有缓冲区 */
return(0);
}
double r8_uniform_ab( double a, double b, int &seed )
{
{
int i4_huge = 2147483647;
int k;
double value;
if ( seed == 0 )
{
std::cerr << "\n";
std::cerr << "R8_UNIFORM_AB - Fatal error!\n";
std::cerr << " Input value of SEED = 0.\n";
exit ( 1 );
}
k = seed / 127773;
seed = 16807 * ( seed - k * 127773 ) - k * 2836;
if ( seed < 0 )
{
seed = seed + i4_huge;
}
value = ( double ) ( seed ) * 4.656612875E-10;
value = a + ( b - a ) * value;
return value;
}
}
void *crossover (chrom popnext[4]) // 函数：交叉操作；
{
int random ;
int i ;
//srand(time(0));
random=rand (); // 随机产生交叉点；
random=((random %5)+1); // 交叉点控制在0到5之间；
for(i =0;i< random;i ++)
{
popnext[2].bit [i]= popnext[0].bit [i]; // child 1 cross over
popnext[3].bit [i]= popnext[1].bit [i]; // child 2 cross over
}
for(i =random; i<6;i ++) // crossing the bits beyond the cross point index
{
popnext[2].bit [i]= popnext[1].bit [i]; // child 1 cross over
popnext[3].bit [i]= popnext[0].bit [i]; // chlid 2 cross over
}
for(i =0;i<4; i++)
{
popnext[i ].fit= y(x (popnext[ i])); // 为新个体计算适应度值；
}
for(i =0;i<4; i++)
{
printf("\nCrossOver popnext[%d]=%d%d%d%d%d%d value=%d fitness = %d",i, popnext[i ].bit[5], popnext[i ].bit[4], popnext[i ].bit[3], popnext[i ].bit[2], popnext[i ].bit[1], popnext[i ].bit[0], x(popnext [i]), popnext[i ].fit);
// 输出新个体；
}
return(0);
}
void *mutation (chrom popnext[4]) // 函数：变异操作；
{
int random ;
int row ,col, value;
//srand(time(0));
random=rand ()%50; // 随机产生到之间的数；
//变异操作也要遵从一定的概率来进行，一般设置为0到0.5之间
//
if(random ==25) // random==25的概率只有2%，即变异率为，所以是以小概率进行变异！！
{
col=rand ()%6; // 随机产生要变异的基因位号；
row=rand ()%4; // 随机产生要变异的染色体号；
if(popnext [row]. bit[col ]==0) // 1变为；
{
popnext[row ].bit[ col]=1 ;
}
else if (popnext[ row].bit [col]==1) // 0变为；
{
popnext[row ].bit[ col]=0;
}
popnext[row ].fit= y(x (popnext[ row])); // 计算变异后的适应度值；
value=x (popnext[ row]);
printf("\nMutation occured in popnext[%d] bit[%d]:=%d%d%d%d%d%d value=%d fitness=%d", row,col ,popnext[ row].bit [5],popnext[ row].bit [4],popnext[ row].bit [3],popnext[ row].bit [2],popnext[ row].bit [1],popnext[ row].bit [0],value, popnext[row ].fit);
// 输出变异后的新个体；
}
return(0);
}

同时需要注意的是在利用遗传算法过程中需要较大的种群数量或者设置较高的迭代次数，否则容易过早地到达稳态。

如在计算方程y=-x^2+5的最大值时，所选择的是以6bit来对个体进行编码，其中1bit为符号位。所以，基因型的范围为-32~+31。

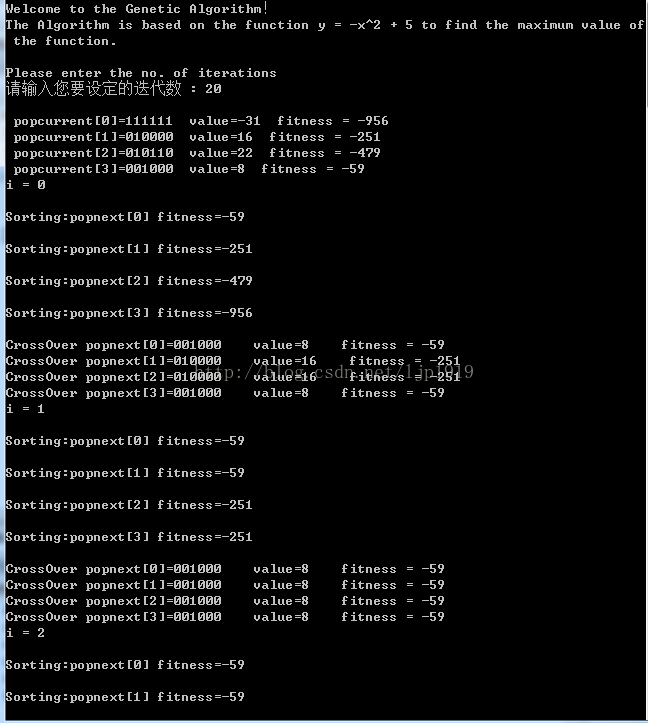
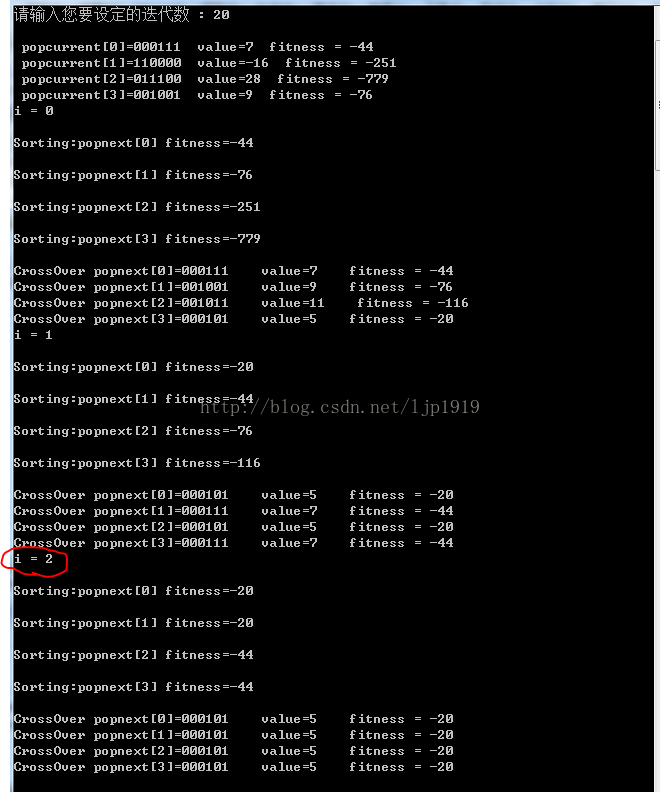
而且选择的个体数量为4个，易于过早到达平衡。如下图所示，所设置的迭代次数为20，但是在迭代两次就已经使得个体无差异，无法再继续以交叉组合出更高适应性的基因型。唯一可以期望的是基因突变，但是突变所设置的是小概率事件，本文所设置的约为2%。那么需要增大迭代次数，以增大基因突变的次数，以避免过早陷入最优。