由于矩阵的乘法满足结合律,故计算矩阵的连乘积可以有许多不同的计算次序。这中计算次序可以用加括号的方式来确定。例如,矩阵连乘积A1A2A3A4可以有一下5种不同的完全加括号方式:
(A1(A2(A3A4)))
(A1((A2A3)A4))
((A1A2)(A3A4))
((A1(A2A3))A4)
(((A1A2)A3)A4)
矩阵A和B可乘的条件是矩阵A的列数等于矩阵B的行数。若A是一个p*q的矩阵,B是一个q*r的矩阵,其乘机C=AB是一个p*r的矩阵,总共需要pqr次数乘。
为了说明在计算矩阵连乘积时,加括号方式对整个计算量的影响,我们考察计算3个矩阵A1A2A3的连乘积的例子。这3个矩阵的尺寸分别为10*100,100*5和5*50。若以((A1A2)A3)这种方式计算,3个矩阵的连乘积需要的数乘次数为7500。若以(A1(A2A3))这种方式计算,所需的数乘次数为75000。显然,在即算矩阵连乘积时,加括号方式对计算量有很大影响。
于是,人们自然会提出矩阵连乘积的最优计算次序问题。即对于给定的n个矩阵,如何确定计算矩阵连乘积的计算次序(完全加括号方式),使得以此计算次序计算矩阵连乘积所需的数乘次数最少。
穷举搜索法不是一个有效算法,它的时间复杂度是随n的增长呈指数增长的。下面考虑用动态规划法解矩阵连乘积的最优计算次序问题。
1.分析最优解的结构
设计求解具体问题的动态规划算法的第一步是刻画该问题的最优解的结构特征。我们将矩阵连乘积AiAi+1....Aj简记为A[ i : j ]。考察计算A[ 1: n]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,1<=k<n,则其相应的完全加括号形式为((A1...Ak)(Ak+1...An))。以此次序,总的计算量为A[ 1 : k ]的计算量加上A[ k+1 : n ]的计算量, 再加上A[ 1 : k ]和A[ k+1 : n ]相称的计算量。
这个问题的关键特征是:计算A[ 1 :n ]的最优次序所包含的计算矩阵子链a[ 1 : k ]和A[ k+1 : n ]的次序也是最优的。因此,矩阵连乘积计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可以用动态规划算法求解的显著特征。
2.建立递归关系
设计动态规划算法的第二步就是递归地定义最优值。对于矩阵连乘积的最有计算次序问题,设计算A[ i : j ], 1<=i<=j<=n,所需的最少数乘次数为m[ i ][ j ],则原问题的最优值为m[ 1 ][ n]。
当i=j时,A[ i : j ]=Ai,为单一矩阵,无需计算,因此m[ i ][ i ]=0。
当i < j时,可以利用最优子结构的性质来计算m[ i ][ j ]。事实上,若计算A[ i : j ]的最优次序在Ak和Ak+1之间断开,i<=k<j,则m[ i ][ j ]=m[ i ][ k ]+m[k+1][ j ]+Pi-1*Pk*Pj。其中Pi表示第i个矩阵的列数,也是第i-1个矩阵的行数,P0表示第一个矩阵的行数。由于在计算时并不知道断开点k的位置,所以k还未定。不过k的位置只有j-i个可能。从而m[ i ][ j ]可以递归地定义为
当i=j m[ i ][ j ] = 0
当i<j m[ i ][ j ] = min{ m[ i ][ k ]+m[ k+1 ][ j ]+Pi-1*Pk*Pj }
m[ i ][ j ]给出了最优值,即计算A[ i : j ]所需的最少数乘次数。同时还确定了计算A[ i : j ]的最优次序中的断开位置k,也就是说,对于这个k有
m[ i ][ j ]=m[ i ] [ k ]+m[ k+1 ][ j] + Pi-1*Pk*Pj
若将对应于m[ i ][ j ]的断开位置k记为s[ i ][ j ], 在计算最优值m[ i ][ j ]后,可以递归地有s[ i ][ j ]构造出相应的最优解。
3.计算最优值
根据计算m[ i ][ j ]的递归式,容易写一个递归算法计算m[ 1 ][ n ]。但是简单地递归将好费指数计算时间。在递归计算时,许多子问题被重复计算多次。这也是该问题可以用动态规划算法求解的又一显著特征。
用动态规划算法解决此问题,可依据其递归是以自底向上的方式进行计算。在计算的过程中,保存以解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算。
以下为测试代码
#include <iostream>
using namespace std;
const int maxsize = 10000;
int l[maxsize][maxsize] = { 0 };
int s[maxsize][maxsize] = { 0 };
int p[maxsize] = { 0 };
void MatrixChain(int n);
void Trackback(int i, int j);
int main() {
int n = 6;
for (int i = 0; i <= n; i++) {
cin >> p[i];
}
MatrixChain(n);
Trackback(1, n);
cout << l[1][6] <<endl;
return 0;
}
/*
将二维矩阵填冲
p数组用来存储每个矩阵的行列数 例如 矩阵A1为P[0]* P[1] 矩阵A2为P[1]*P[2]
n为矩阵的数量
l[i][j] 表示从第i个矩阵到第j个矩阵的最少乘法次数
s[i][j] 表示从第i个矩阵到第j个矩阵的最少乘法次数此时矩阵断开的地方
递归公式为 m[i][j] = min{m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]}
*/
void MatrixChain( int n) {
for (int i = 1; i <= n; i++) {
l[i][i] = 0;
}
for (int r = 2; r <= n; r++) { //作为填充的范围,n行n列,从1->2, 1->3,1->4,....1->n
for (int i = 1; i <= n - r + 1; i++) { //l、s二维数组的行标,即从第几个开始计算矩阵,如l[i][j] 从i到j
int j = i + r - 1; //列,目标
l[i][j] = l[i][i] + l[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (int k = i + 1; k < j; k++) {
int t = l[i][k] + l[k + 1][j] + p[i - 1] * p[k] * p[j];
if (t < l[i][j]) {
l[i][j] = t;
s[i][j] = k;
}
}
}
}
}
/*
按断点矩阵s指示的加括号方式输出l[i][j]的最优计算次序
*/
void Trackback(int i, int j ) {
if (i == j)
return;
Trackback(i, s[i][j]);
Trackback(s[i][j] + 1, j);
cout << "Multiply A" << i << "," << s[i][j];
cout << "and A" << (s[i][j] + 1) << "," << j << endl;
}
/*
30 35 15 5 10 20 25
*/算法matrix_chain首先计算出m[ i ][ i ]=0,然后再根据递归式,按照矩阵链长递增的方式依次计算m[ i ][ i+1 ],m[ i ][ i+2 ]……在计算m[ i ][ j ]时,只是用到已计算出的m[ i ][ k ]和m[ k+1 ][ j ]。
比如,计算矩阵连乘积A1A2A3A4A5A6,其尺寸分别为:
A1 : 30*35 A2 : 35*15 A3 : 15*5 A4 : 5*10 A5 : 10*20 A6 : 20*25
动态规划算法matrix_chain计算m[ i ][ j ]先后次序如图所示,计算结果为m[ i ][ j ]和s[ i ][ j ],其中第0行和第0列没有使用。
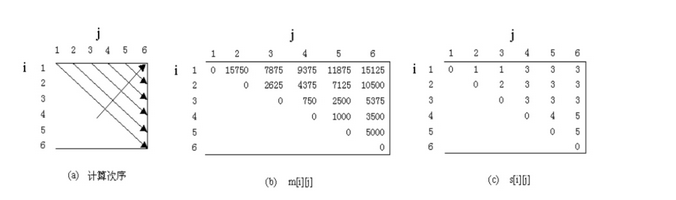
例如,在计算m[2][5]时,依递归式有
所以m[2][5] = 7125,且k=3,因此,s[2][5]=3。
算法matrix_chain的主要计算量取决于程序中对r,i和k的三重循环。循环体内的计算量为O( 1 ),而三重循环的总次数为O( n^3 )。因此,概算发的计算时间的上界为O(n^3)。所占用的空间显然为O(n^2)。由此可见动态规划算法比穷举搜索法要有效的多。
4.构造最优解
动态规划算法的第四布是构造问题的最优解。算法matrix_chain只是计算出了最优值,并未给出最优解。也就是说,通过matrix_chain的计算,只是到最少数乘次数,还不知道具体应按什么次序来做矩阵乘法才能达到最少的数乘次数。
事实上,matrix_chain已记录了构造最优解所需要得全部信息。s[ i ][ j ]中的数表明,计算矩阵链A[ i : j ]的最佳方式应在矩阵Ak和Ak+1之间断开,级最优的加括号方式应为(A[ i : k ])(A[ k+1 : j ])。因此,从s[ 1 ][ n ]记录的信息可知计算A[ 1 : n ]的最优加括号方式为(A[ 1 : s[ 1 ][ n ]})(A[s[ 1 ][ n ]+1 : n])。同理可以最终确定A[ 1 : n ]的最优完全加括号方式,即构造出问题的一个最优解。








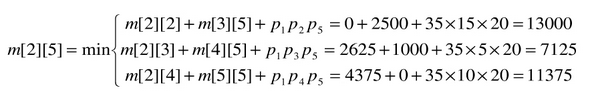














 158
158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








