动手学深度学习（PyTorch版）笔记 03 线性神经网络

3. 线性神经网络

3.1 线性回归

3.1.1 线性回归的基本元素

线性模型

回归（regression）是能为一个或多个自变量与因变量之间关系建模的一类方法。

线性回归的基本假设：

1. 假设自变量 $\mathbf{x}$ 和 因变量 $y$ 之间的关系是线性的，即 $y$ 可以表示为 $\mathbf{x}$ 中元素的加权和。（通常允许包含观测值的一些噪声）;
2. 假设任何噪声都比较正常，如噪声遵循正态分布。

当我们的输入包含 $d$ 个特征时，我们将预测结果 $\hat{y}$ （通常使用“尖角”符号表示 $y$ 的估计值）表示为：
$$\hat{y}=w_1{x}_1+\dots +w_d{x}_d+b$$
其中， $w$ 称为权重（weight），决定了每个特征对预测值的影响； $b$ 称为偏置（bias），指当所有特征值都为 0 时，预测值应该是多少。

上式可采用向量的点积形式表示为：
$$\hat{y}={\mathbf{w}}^{\top }\mathbf{x}+b$$
其中，$\mathbf{x}\in {\mathbb{R}}^d$，$\mathbf{w}\in {\mathbb{R}}^d$

此外，若 $\mathbf{X}$ 是一个特征集合 $\mathbf{x}\in {\mathbb{R}}^{n\times d}$，$\mathbf{w}\in {\mathbb{R}}^d$，预测值 $\hat{\mathbf{y}}\in {\mathbb{R}}^n$，上式可以表示为：
$$\hat{\mathbf{y}}=\mathbf{Xw}+b$$
给定训练数据特征 $\mathbf{X}$ 和对应的已知标签 $\mathbf{y}$ ， 线性回归的目标是找到一组权重向量 $\mathbf{w}$ 和偏置 $b$： 当从 $\mathbf{X}$ 的同分布中取样的新样本特征时， 这组权重向量和偏置能够使新样本的预测结果的误差尽可能小。

损失函数

损失函数（loss function）能够量化目标的实际值与预测值之间的差距，是一种模型质量的度量方式。通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为 0 。回归问题中最常用的损失函数是平方误差函数。当样本 $i$ 的预测值 为 ${\hat{y}}^{(i)}$，其相应的真实标签为 $y^{(i)}$ 时，平方误差可以定义为以下公式：
$$l^{(i)}(\mathbf{w},b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2$$
在训练模型时，我们希望寻找一组参数 $\left({\mathbf{w}}^{\ast },b^{\ast }\right)$，这组参数能最小化在所有训练样本上的总损失。如下式:
$${\mathbf{w}}^{\ast },b^{\ast }=\underset{\mathbf{w},b}{\mathrm{argmin}}L(\mathbf{w},b)$$

解析解

线性回归的解可以用一个公式简单地表达出来， 这类解叫作解析解（analytical solution）。对于线性回归问题来说，我们的目标是最小化$$\Vert \mathbf{y}-\mathbf{Xw}{\Vert }^2$$，当损失关于 $\mathbf{w}$ 的导数为 0 时，我们可以得到解析解：
$${\mathbf{w}}^{\ast }={\left({\mathbf{X}}^{\top }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\top }\mathbf{y}$$

梯度下降

梯度下降（gradient descent）：通过不断地在损失函数递减的方向上更新参数来降低误差。
$$(\mathbf{w},b)\leftarrow (\mathbf{w},b)-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\partial }_{(\mathbf{w},b)}{l}^{(i)}(\mathbf{w},b)$$
其中， $ |\mathcal{B}| $ 表示每个小批量中的样本数，这也称为批量大小 (batch size)。 $\eta$ 表示学习率 (learning rate)。批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。这些可以调整但不在训练过程中更新的参数称为超参数 (hyperparameter)。调参 (hyperparameter tuning) 是选择超参数的过程。超参数通常是我们根据训练迭代结果来调整的，而训练迭代结果是在独立的验证数据集（validation dataset）上评估得到的。

预测

给定特征估计目标的过程通常称为预测（prediction）或推断（inference）。

3.1.2 矢量化加速

在训练模型时，我们希望同时处理整个小批量的样本，此时，需要对计算进行矢量化，从而利用线性代数库，而不使用 for 循环，以此来加速训练过程。

例如，对于两个 10000 维向量相加，若使用 for 循环逐位计算，将耗时 0.16749 sec ，而若是使用线性代数库进行矢量运算的话，仅耗时 0.00042 sec 。

定时器相关代码：

import time

class Timer:  #@save
    """记录多次运行时间"""
    def __init__(self):
        self.times = []
        self.start()

    def start(self):
        """启动计时器"""
        self.tik = time.time()

    def stop(self):
        """停止计时器并将时间记录在列表中"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """返回平均时间"""
        return sum(self.times) / len(self.times)

    def sum(self):
        """返回时间总和"""
        return sum(self.times)

    def cumsum(self):
        """返回累计时间"""
        return np.array(self.times).cumsum().tolist()

3.1.3 正态分布与平方损失

正态分布（normal distribution），也称为高斯分布（Gaussian distribution），若随机变量 $X$ 服从一个平均数为 $\mu$ 、标准差为 $\sigma$ （方差 ${\sigma }^2$ ）的正态分布，则记为:
$$X\sim N\left(\mu ,{\sigma }^2\right)$$
则其概率密度函数为：
$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
假设观测中包含噪声，其中噪声服从正态分布，则包含噪声的 $y$ 的分布如下式：
$$y={\mathbf{w}}^{\top }\mathbf{x}+b+ϵ$$
其中，$ϵ\sim \mathcal{N}\left(0,{\sigma }^2\right)$ 。因此，上式可以看作： $ϵ=y-{\mathbf{w}}^{\top }\mathbf{x}-b$

因此，我们现在可以写出通过给定的 $\mathbf{x}$ 观测到特定 $y$ 的似然（likelihood）：
$$P(y\mid \mathbf{x})=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{1}{2{\sigma }^2}{\left(y-{\mathbf{w}}^{\top }\mathbf{x}-b\right)}^2\right).$$
补充说明：这边，我们可以把 $ϵ=y-{\mathbf{w}}^{\top }\mathbf{x}-b$ 看作是网络的计算值与真实值之间的偏差，而这个偏差是符合正态分布的。此外， $y$ 应该是一个线性值，也就是说 $y$ 可以大于 1。同时，在给定 $x$ 的情况下（观测值 ${\mathbf{w}}^{\top }\mathbf{x}+b$ ）预测真实值 $y$ 的概率应该是 $P(y\mid \mathbf{x})$（因为噪声的存在，且噪声符合正态分布，因此该似然值符合正态分布，若不存在噪声，理论上，在 $\mathbf{x}$ 的情况下预测出真实的 $y$ 值的似然应该是1。例如 $y$ 的真实值为 $y=1$ ，则似然 $P(y=1\mid \mathbf{x})=1\text{ 且 }P(y=other\mid \mathbf{x})=0$）。当 ${\mathbf{w}}^{\top }\mathbf{x}+b$ 越接近于 $y$ 时（ $y-{\mathbf{w}}^{\top }\mathbf{x}-b$ 越接近均值 $\mu =0$ ），该值越大，因此这个概率值在 $y={\mathbf{w}}^{\top }\mathbf{x}+b$ 时，将达到最大。而我们需要的做的是，确定一个 $w,b$ ，使得 ${\mathbf{w}}^{\top }\mathbf{x}+b$ 能够尽可能的接近 $y$ ，也就是，需要令 $P(y\mid \mathbf{x})$ 尽可能的大。

现在，根据极大似然估计法，参数 $\mathbf{w}$ 和 $ b $ 的最优值是使整个数据集的似然最大的值（这边是一个相乘的运算，也就是计算每一次都预测正确的概率）:
$$P(\mathbf{y}\mid \mathbf{X})=\prod _{i=1}^{n}p\left(y^{(i)}\mid {\mathbf{x}}^{(i)}\right).$$
由于最大化函数较为困难，因此，将上式取负对数，将问题调整为取最小化负对数似然 $-\log P(\mathbf{y}\mid \mathbf{X})$ ：
$$-\log P(\mathbf{y}\mid \mathbf{X})=\sum _{i=1}^n\frac{1}{2}\log \left(2\pi {\sigma }^2\right)+\frac{1}{2{\sigma }^2}{\left(y^{(i)}-{\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}-b\right)}^2$$

3.2 线性回归的从零开始实现

1. torch.normal(mean, std, size=None) ：mean：正态分布的均值；std：正态分布的标准差；size：生成的随机数的形状， size 应是一个元组，若要表示包含 $n$ 个元素的一维向量，元组表示为 (n,)
2. list(range(num_examples)) 是一个用于生成一个包含从 0 到 num_examples - 1 的整数的列表。range() 是一个内置函数，它返回一个表示指定范围的整数序列的对象。当我们将 range() 的结果传递给 list() 函数时，它会将这个整数序列转换为一个列表。注意：range() 函数在Python 3中返回的是一个可迭代对象，而不是一个实际的列表。如果需要一个列表，可以使用 list() 函数将 range() 的结果转换为列表。
3. yield ：带有 yield 的函数在 Python 中被称为 generator （生成器），当首次调用 generator 时不会执行任何函数中的代码，直到调用 __next__() 时才会执行函数中的代码并返回一个迭代值，当下一次调用 __next__() 时代码会从 yield 的下一个语句开始执行。在 for...in... 遍历中， __next__() 会自动执行。
4. with torch.no_grad(): ： torch.no_grad() 是 PyTorch 中的一个上下文管理器，在 with torch.no_grad(): 中的计算不会计算梯度，在该上下文中对张量的操作不会被记录到计算图中。通常用于不需要计算梯度的前向传播场景或者梯度更新场景。
5. with ：python 中的 with 语句被用于异常处理，封装了 try...except...finally 编码范式。 with 上下文表达式 as 变量: 的执行过程是，首先执行上下文管理器的 __enter__ 函数，它的返回值会赋值给 as 后面的变量，当 with 中的语句执行完成后，将会调用上下文管理器的 __exit__ 函数来清理资源。例如，使用 with 打开一个文件，当 with 中的语句执行完成后，将会自动关闭文件。

3.3 线性回归的简介实现

1. *变量 ：当我们在变量名前加上* 符号时，它的作用是将一个可迭代对象（比如列表或元组）拆分成单个的元素，这个过程也被称为“拆包”。这意味着可以将一个列表或元组的元素作为单独的参数传递给函数。补充：在函数定义中，将一个星号放在变量名前面表示接受任意数量的位置参数。这意味着函数可以接受不确定数量的参数，并将它们作为一个元组传递给函数。

def my_function(*args):
    for arg in args:
        print(arg)

my_function(1, 2, 3)
'''
output:
1
2
3
'''
my_list = [1, 2, 3]
my_function(*my_list)
'''
output:
1
2
3
'''
numbers = [1, 2, 3, 4, 5]
first, *rest, last = numbers

print(first)  # 输出 1
print(rest)   # 输出 [2, 3, 4]
print(last)   # 输出 5

2. Sequential类：Sequential 类将多个层串联在一起。 当给定输入数据时，Sequential 实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。

3. nn.Sequential(nn.Linear(2, 1)) ：创建一个全连接层，第一个参数指定输入特征形状，第二个参数指定输出特征形状。

4. nn.MSELoss() ：均方误差损失。

5. trainer = torch.optim.SGD(net.parameters(), lr=0.03) ：创建一个采用SGD算法的优化器，需指定优化的参数 （可通过net.parameters()从模型中获得）以及优化算法所需的超参数字典。

6. trainer.step() ：更新模型参数。

在每个迭代周期里，我们将完整遍历一次数据集（train_data），不停地从中获取一个小批量 的输入和相应的标签。对于每一个小批量，我们会进行以下步骤:

1. 通过调用 $\text{net}(\mathrm{X})$ 生成预测并计算损失 $l$ （前向传播）。
2. 通过进行反向传播来计算梯度。
3. 通过调用优化器来更新模型参数。

3.4 softmax回归

对于多类别的预测任务，我们需要一个具有多输出的模型，也就需要和输出一样多的仿射函数，每一个输出都有它对应的仿射函数。例如，对于一个具有4个特征、3个输出的任务，将需要12个标量来表示权重。
$$\begin{array}{l}{o}_1=x_1{w}_{11}+x_2{w}_{12}+x_3{w}_{13}+x_4{w}_{14}+b_1,\\ o_2=x_1{w}_{21}+x_2{w}_{22}+x_3{w}_{23}+x_4{w}_{24}+b_2,\\ o_3=x_1{w}_{31}+x_2{w}_{32}+x_3{w}_{33}+x_4{w}_{34}+b_3.\end{array}$$

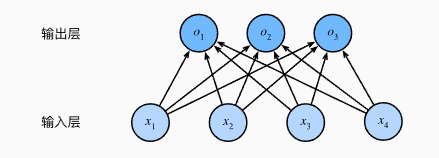
为了确保最终输出的概率值总和为1，且拉开各个输出概率之间的距离，我们采用softmax函数：
$$\hat{\mathbf{y}}=\mathrm{softmax}(\mathbf{o})\text{ 其中 }{\hat{y}}_j=\frac{\exp \left(o_j\right)}{{\sum }_k\exp \left(o_k\right)}$$

3.5 图像分类数据集

1. PIL ：Python Imaging Library，python平台的一个图像处理库，由于PIL仅支持到python 2.7，因此志愿者在PIL的基础上开发了兼容版本，即 pillow。PIL 提供了一系列图像处理相关的功能，例如打开图像、裁剪图像、添加滤镜等。
2. torchvision.transforms.ToTensor() ：通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，并除以255使得所有像素的数值均在0～1之间。（link）
3. torchvision.datasets ：提供各种内置数据集，例如 CIFAR10、MNIST 等。（link）
4. axes = axes.flatten() ：在用plt.subplots画多个子图中， axes = axes.flatten() 将 axes 由 $nm$ 的Axes组展平成 $1\times nm$ 的Axes组。前者需要使用 axes[i][j] 调用，而后者则可以直接使用 axes[i] 调用。（link）

3.6 softmax回归的从零开始实现

1. net.train() 与 net.eval() ：如果一个模型有Dropout与BatchNormalization，那么它在训练时要进行Dropout或者更新BatchNormalization参数，而在测试时不再需要Dropout或BN。此时，要用 net.train() 和 net.eval() 进行区分。在没有涉及到BN与Dropout的模型，这两个函数没什么用。

3.7. softmax回归的简洁实现

1. net.apply(fn) ：对每一个子模块递归应用函数 fn ，典型的做法是初始化模型参数。 （link）

@torch.no_grad()
def init_weights(m):
    print(m)
    if type(m) == nn.Linear:
        m.weight.fill_(1.0)
        print(m.weight)
net = nn.Sequential(nn.Linear(2, 2), nn.Linear(2, 2))
net.apply(init_weights)