Introduction to Algorithm - Summary of Chapter 8 - Sorting in Linear Time

Introduction of The Chapter

Comparison sorts : The sorted order is based only on comparison between the input elements.

Stable : Numbers with the same value appear in the output array in the same order as they do in the input array.
The property of stability is important only when there are the satellite data carried by the key element.

In place : During the execution of the sorting, only a constant number of elements of the input array are ever stored outside the array.

Any sort comparison must make $\Omega$(n lg n) comparison in the worst case to sort n elements. The sort comparisons which we have learnt are insertion sort, merge sort, heap sort and quick sort.

---

Lower bounds for sorting

comparison sort algorithm only compare between element elements to gain order without inspecting the values of the elements or gaining order information about the in any other way.

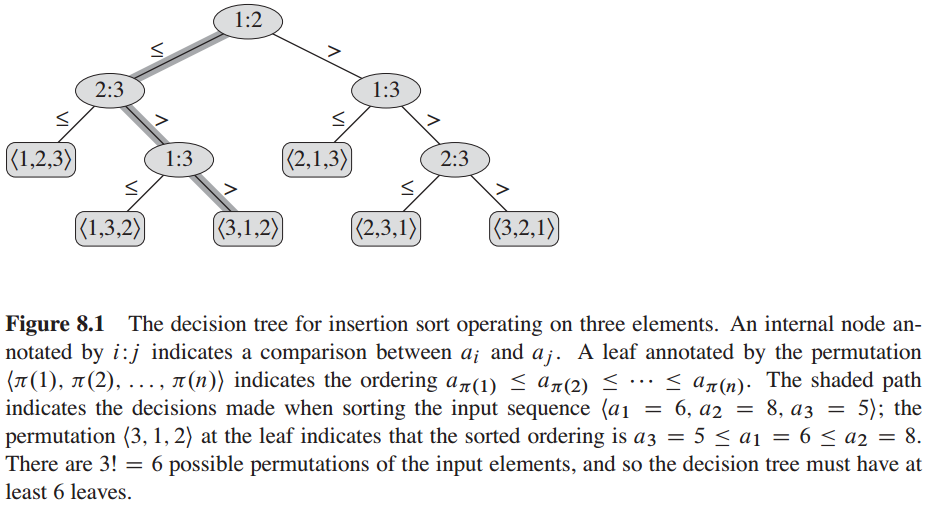
decision tree : A full binary tree that represents the comparison between elements that are performed by the particular sorting algorithm operating on an input of a given size.

The particular execution of the sorting algorithm corresponds to tracing a simple path from the root of the decision tree down to a leaf. So, each leaf corresponds a actual execution of the sorting algorithm.

The worst case number of comparisons for a given comparison sorting algorithm equals the height of its decision tree.

Theorem 8.1
Any comparison sort algorithm requires $\Omega$(n lg n) comparison in the worst case.

Corollary 8.2
heap sort and merge sort are asymptomatically optimal comparison sort.

---

Counting sort

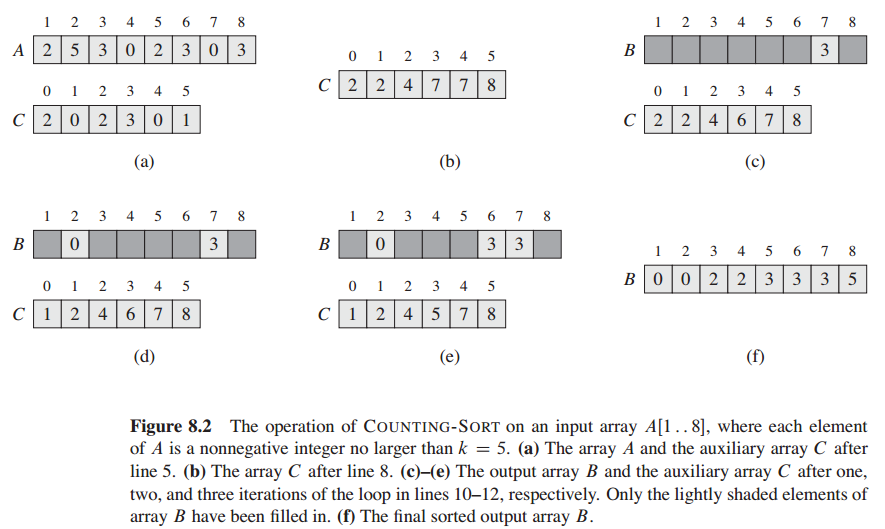
Counting sort : assumes that each of the n input elements is an integer in the range of 0 to k. It determines the number of element less than the each of the input integer x, and uses the information to place element x directly into to its position in the output array.The counting sort uses the actual values of the elements to index into an array.

Counting-Sort(A, B, k)
    let C[0..k] be a new array
    for i=0 to k
        C[i] = 0
    for i=0 to A.length 
        C[A[i]] = C[A[i]] + 1
    //now C[i] contains the number of elements equal to i.
    for i=0 to k
        C[i] = C[i] + C[i-1]
    //now C[i] contains the number of elements equal or less than i.
    for i=A.length downto 1
        B[C[A[i]]] = A[i]
        C[A[i]] = C[A[i]] - 1

The counting sort time is $\Theta$( n + k ) = $\Theta$ (n).Not in place. stability .

---

Radix sort

Radix dort : regards the each of n input elements as a d-digit integer. It sort on the least-significant digit first, then it sort the entire deck again on the second-least significant digit. The process continues until elements have been sorted on all d digits.

Radix-Sort (A, d)
    for i=1 to d
        use a stable sort to sort array A on digit i
    //digit 1 is the least significant digit

The Radix-Sort must be stable, but in place or not depend on choosing of the called sort algorithm.

Lemma 8.3
Given n d-digit numbers in which each digit can take on up to k possible values, Radix-Sort correctly sorts these numbers in $\Theta$ ( d ( n+k) ) time if the stable sort it uses takes $\Theta$ ( n+k ) time.

Lemma 8.4
Given n b-bit number and any positive integer $r \le b$ , Radix-Sort sorts these numbers in $\Theta ( (b/r)(n+2^{r}) )$ time if the stable sort it uses take on $\Theta (k+n)$ time for inputs in the range of 0 to k.

How to choose the value of r to make the expression $( (b/r)(n+2^{r}) )$ minimize ? If $b<\lfloor lg n \rfloor$, choosing $r=b$, else choosing $r=lg n$.

---

Bucket sort

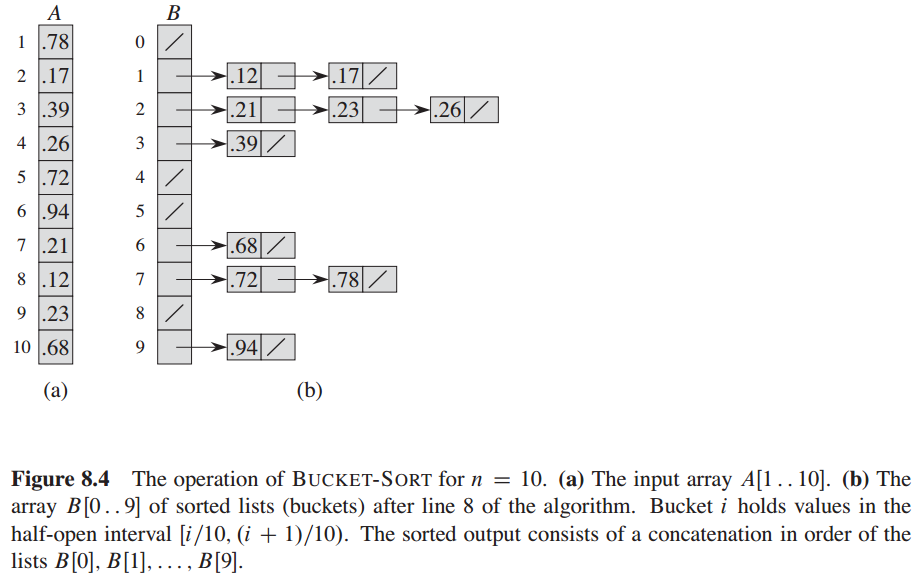
Bucket sort : divides the interval $\lbrack0，1)$ into n equal-sized subintervals, or buckets ,and then distributes the n input number into the buckets.To produce the output, we simple sort the numbers in each bucket and then go through the buckets in order, listing the elements in each.

Bucket-Sort (A)
    let B[0..n-1] be a new array 
    n = A.length 
    for i=0 to n-1
        make B[i] an empty list
    for i=1 to n
        insert A[i] into list B[ |nA[i]| ] 
        //B[ $\lfloor nA[i] \rfloor$ ] 
    for i=0 to n-1
        sort list B[i] with insertion sort 
    concatenate the the list B[0..n-1] together in order 

The bucket sort expection of running time is $\Theta (n) + n*O(2-1/n) = \Theta (n)$, but the worst-time is $\Theta (n^2)$.
Stability . Not in place .

Some of above content refere to “Introduction to Algorithm”.