Introduction to Algorithm - Summary of Chapter 6 - Heapsort_show that the worst-case running time of \text{max-CSDN博客

本文链接：https://blog.csdn.net/u011594482/article/details/49742559

Introduction of The Chapter

Heapsort : It has running time of $\Theta (nlgn )$ , and is in place ,but not stabile .

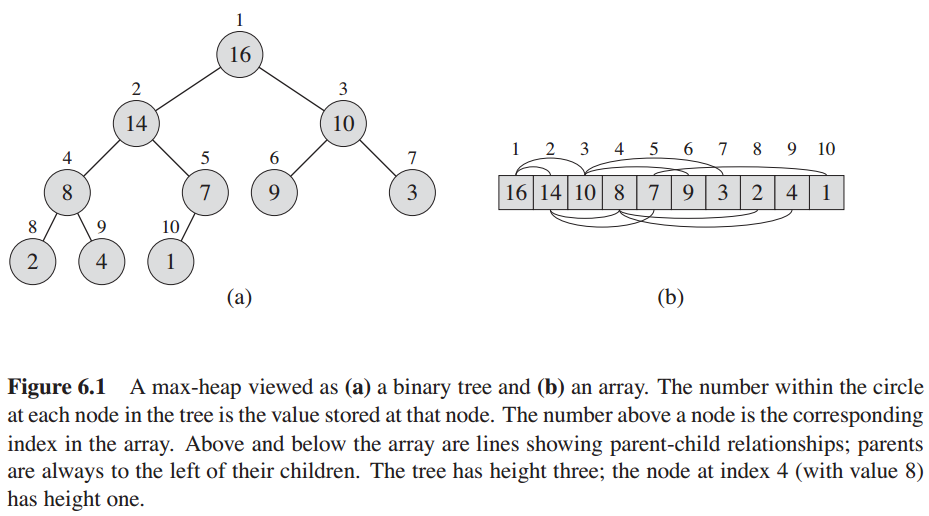
Heaps

Heap is a tree which keeps a special order. It is an array object that we can view as a nearly complete binary tree in the actual store.

The show of heap's parent-children relationship

There are two kinds of heap : Max-heap and Min-heap.

In a Max-heap , the value of a node is at most the value of its parent. The Max-heap is used in Heapsort.

In a Min-heap , the value of a node is at least the value of its parent.the Min-heap is used in the priority queue.

The height of a node in a heap is the number of edges on the longest simple downward path from the node to a leaf.

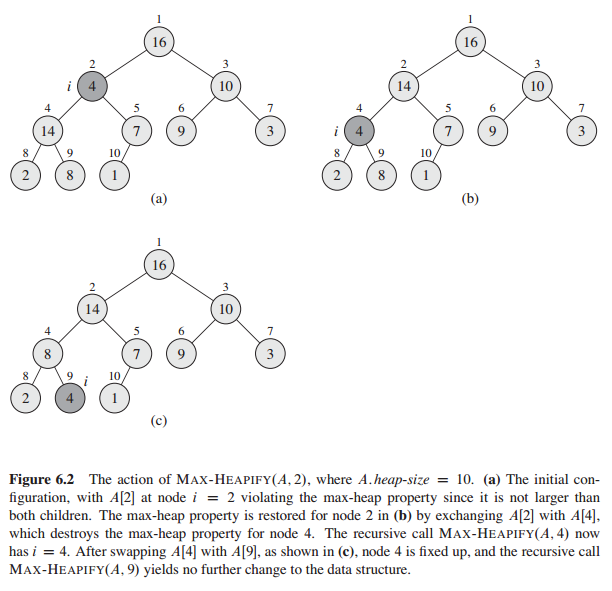
Maintaining the heap property

Max-Heapify (A, i)
    l = LeftChild (i);
    r = rightChild (i);
    if l<= A.heap-size && A[i]<A[l]
        lagest = l
    else lagest = i
    if r<=A.heap-size && A[i]<A[r]
        lagest = r
    if lagest != i
        exchange A[i] with A[lagest]
        Max-Heapify (a, lagest)

The Max-Heapify assumes the A[i]’s subtrees, left and right subtree , are Max-heap. It takes running time of $\Theta (lgn)$

The show of the Max-Heapify

$T(n) = T( \frac{2}{3} n)+ \Theta (1) = O(lgn)$

The $\frac{2}{3} n$ is the size of the worst case subarray .The first $\frac{1}{3} n$ , is the number of the right subtree. The second $\frac{1}{3} n$ , is the number of a part of the left subtree those height is same to the right subtree. The finally $\frac{1}{3} n$ , is the number of the remainder of left subtree .

In the worst-case, the Max-Heapify runs at least once each layer to the leaf, the layer is $\lfloor lgn \rfloor$ , so the Max-Heapify take running time of $\Omega (lgn)$

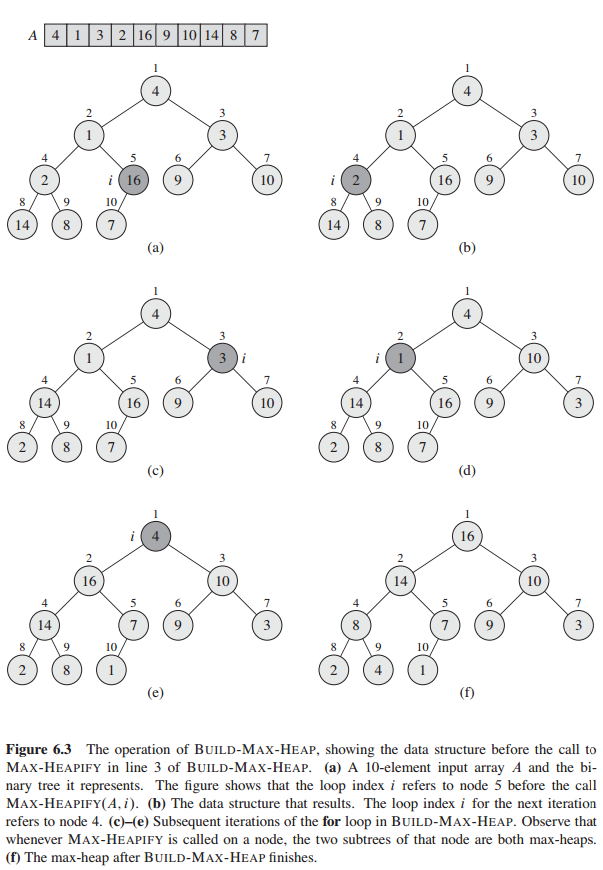
Building a heap

Build-Max-Heap
    A.heap-size = A.leight
    for i=[A.leight/2] downto 1
    // $\lfloor A.leight/2 \rfloor$
        Max_Heapify(A, i)

The show of Build-Max-Heap execution

\sum h = 0 ⌊ l n g ⌋ ⌈ n 2 h + 1 ⌉ O (h) = O (1 2 n \sum h = 0 ⌊ l g n ⌋ h 2 h) = O (n \sum h = 0 ⌊ l g n ⌋ h 2 h) = O (n \sum h = 0 \infty h 2 h) = O (n 1 / 2 ( 1 - 1 / 2 ) 2) = O (n)

$\begin{align} \sum_{h=0}^{\lfloor lng \rfloor}\lceil \frac{n}{2^{h+1}} \rceil O(h) &= O(\frac{1}{2}n\sum_{h=0}^{\lfloor lgn \rfloor} \frac{h}{2^h}) \\&= O(n\sum_{h=0}^{\lfloor lgn \rfloor} \frac{h}{2^h}) \\&= O(n\sum_{h=0}^{\infty } \frac{h}{2^h}) \\&= O(n \frac {1/2}{(1-1/2)^2}) \\& = O(n) \end{align}$

There are at most $\lceil n/2^{h+1}\rceil$ nodes of height h.There is a equalization : $\sum_{k=0}^\infty kx^k = \frac{x}{(1-x)^2}$ , in above proof ,we let x=1/2.

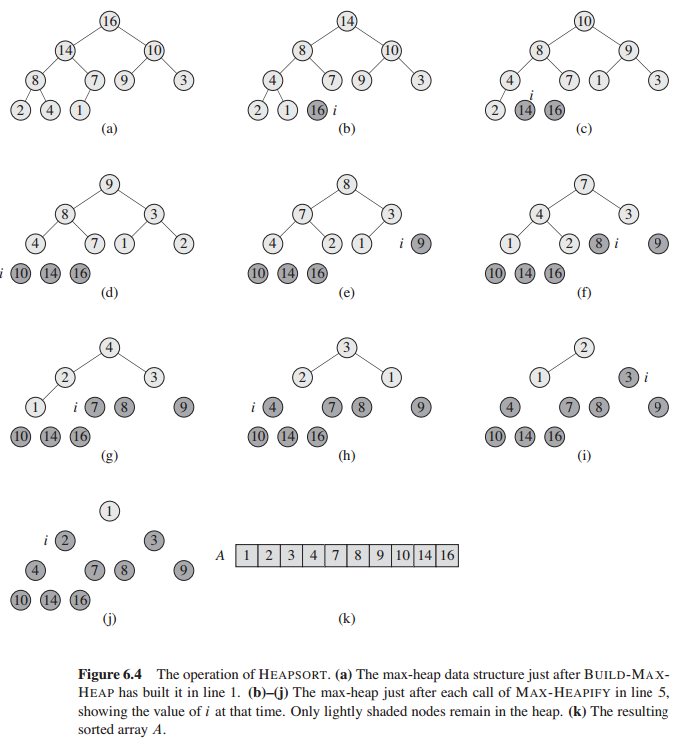
The heapsort algorithm

Heapsort(A)
    Build-Max-Heap(A)
    for i=A.length downto 2
        exchange A[1] with A[i]
        A.heap-size = A.heap-size - 1
        Max-Heapity(A, 1)

The show of Heapsort execution

$O(n) + \sum _{k=2}^{n-1} O(lgn) = O(nlgn)$
$\Omega(n) + \sum _{k=2}^{n-1} \Omega(lgn) = \Omega(nlgn)$

Priority queues

Priority queue : is a data structure for maintaining a set of elements which are inserted, obtained and stored in special order, implemented by Max-heap or Min-Heap.

Heap-Maximum (A)
    return A[1]

Heap-Extract-Max(A)
    max = A[1]
    A[1] = A[A.heap-size]
    A.heap-size = A.heap-size - 1
    Max-Heapity(A, 1)
    return max

Heap-Increase-Key(A, i, key)
    A[i] = key
    while i>1 && A[Parent(i)] < A[i]
        exchange A[i] with A[Parent(i)]
        i = Parent(i)

Max-Heap-Insert(A, key)
    A.heap-size = A.heap-size + 1
    A[A.heap-size] = - $\infty$
    Heap-Increase-key(A, A.heap-size, key)

Some of above content refere to “Introduction to Algorithm”.