压缩感知中的常见测量矩阵及其MATLAB实现代码

原文链接：http://blog.csdn.net/jbb0523/article/details/44700735

题目：压缩感知的常见测量矩阵

        下面首先给出十篇参考文献中有关测量矩阵的叙述，然后以一篇硕士论文中对七种常见测量矩阵的描述依据，给出了这七种常见测量矩阵的MATLAB实现代码，以为以后的研究提供一个参考，由于目前还没有一个简单有效的测量矩阵评价方法，因此这里给出的七种测量矩阵的代码的正确性并没有验证。由于本人对乱引参考文献很受伤，经常按照引用的参考文献对应去找原文却找不到，所以这里都是以截图的方式给出，方便到去文献中找到这里的原文内容。

一、参考文献中常见的测量矩阵

[1]喻玲娟，谢晓春.压缩感知介绍[J].电视技术，2008，32(12)：16-18.

[2]李树涛，魏丹.压缩传感综述[J]. 自动化学报，2009，35(11)：1369-1377.

[3]焦李成，杨淑媛，刘芳，侯彪. 压缩感知回顾与展望[J]. 电子学报，2011，39(7)：1651-1662.

[4]石光明，刘丹华，高大化，刘哲，林杰，王良君. 压缩感知理论及其研究进展[J]. 电子学报，2009，37(5)：1070-1081.

[5]李坤，马彩文，李艳，陈萍.压缩感知重构算法综述[J].红外与激光工程，2013，42(z1)：225-232.

[6]党骙，马林华，田雨，张海威，茹乐，李小蓓. m序列压缩感知测量矩阵构造[J]. 西安电子科技大学（自然科学版），2015，42(2)：215-222.

[7]朱志臻，周崇彬，刘发林，李滨兵，张志达. 用于压缩感知的二值化测量矩阵[J]. 微波学报，2014，30(2)：79-83，96.

[8]王学伟，崔广伟，王琳，贾晓璐，聂伟.基于平衡Gold序列的压缩感知测量矩阵的构造[J]. 仪器仪表学报，2014，35(1)：97-102.

[9]张波，刘郁林，王开.稀疏随机矩阵有限等矩性质分析[J]. 电子与信息学报，2014，36(1)：169-174.

[10]王侠，王开，王青云，梁瑞宇，左加阔，赵力，邹采荣. 压缩感知中的确定性随机观测矩阵构造[J]. 信号处理，2014，30(4)：436-442.

二、常见测量矩阵的MATLAB实现

        下面以文献【吴赟.压缩感知测量矩阵的研究[D]. 西安电子科技大学硕士学位论文，2012】为依据，给出文献中2.2节内容所述的六种测量矩阵MATLAB实现代码，仅为一种参考实现方式，还未验证其正确性。

1、高斯矩阵

        以下代码生成的高斯矩阵方差为1，若为改为1/M，只须将除以根号M即可。

[plain]  view plain  copy

1. function [ Phi ] = GaussMtx( M,N )  
2. %GaussMtx Summary of this function goes here  
3. %   Generate Bernoulli matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   Phi -- The Gauss matrix  
7.   
8. %% Generate Gauss matrix     
9.     Phi = randn(M,N);  
10.     %Phi = Phi/sqrt(M);  
11. end  

2、伯努利矩阵

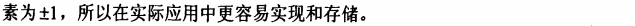
        以下代码是按式(2-8)生成的伯努利矩阵，若要按式(2-9)生成则需使用后半部分注释掉的代码即可。注意代码中用到了MATLAB自带的randi函数，若你的MATLAB版本较低，可能要用randint函数代替，后面若用到此函数则一样要注意这一点。

[plain]  view plain  copy

1. function [ Phi ] = BernoulliMtx( M,N )  
2. %BernoulliMtx Summary of this function goes here  
3. %   Generate Bernoulli matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   Phi -- The Bernoulli matrix  
7.   
8. %% (1)Generate Bernoulli matrix(The first kind)  
9. % 1--P=0.5   -1--P=0.5  
10.     Phi = randi([0,1],M,N);%If your MATLAB version is too low,please use randint instead  
11.     Phi(Phi==0) = -1;  
12.     %Phi = Phi/sqrt(M);  
13. % %% (2)Generate Bernoulli matrix(The second kind)  
14. % % 1--P=1/6   -1--P=1/6  0--2/3  
15. %     Phi = randi([-1,4],M,N);%If your MATLAB version is too low,please use randint instead  
16. %     Phi(Phi==2) = 0;%P=1/6  
17. %     Phi(Phi==3) = 0;%P=1/6  
18. %     Phi(Phi==4) = 0;%P=1/6  
19. %     %Phi = Phi*sqrt(3/M);  
20. end  

3、部分哈达玛矩阵

        由于MATLAB自带的函数hadamard参数有限制，所以程序中首先计算满足要求的参数L，需要注意的是，hadamard参数并不像文献中所述仅为2的整数次幂，而是12的整数倍或20的整数倍或2的整数次幂，详情在MATLAB查看hadamard的help文件。

[plain]  view plain  copy

1. function [ Phi ] = PartHadamardMtx( M,N )  
2. %PartHadamardMtx Summary of this function goes here  
3. %   Generate part Hadamard matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   Phi -- The part Hadamard matrix  
7.   
8. %% parameter initialization  
9. %Because the MATLAB function hadamard handles only the cases where n, n/12,  
10. %or n/20 is a power of 2  
11.     L_t = max(M,N);%Maybe L_t does not meet requirement of function hadamard  
12.     L_t1 = (12 - mod(L_t,12)) + L_t;  
13.     L_t2 = (20 - mod(L_t,20)) + L_t;   
14.     L_t3 = 2^ceil(log2(L_t));  
15.     L = min([L_t1,L_t2,L_t3]);%Get the minimum L  
16. %% Generate part Hadamard matrix     
17.     Phi = [];  
18.     Phi_t = hadamard(L);  
19.     RowIndex = randperm(L);  
20.     Phi_t_r = Phi_t(RowIndex(1:M),:);  
21.     ColIndex = randperm(L);  
22.     Phi = Phi_t_r(:,ColIndex(1:N));  
23. end  

4、部分傅里叶矩阵

        以下代码生成的是部分傅里叶矩阵，这里要提的一点是，有关“归一化”的概念在网上说法不一，一种说法是向量除以向量各项之和，另一种说法是向量除以向量的2范数（各项平方之和再开方），这里采用后者。

[plain]  view plain  copy

1. function [ Phi ] = PartFourierMtx( M,N )  
2. %PartFourierMtx Summary of this function goes here  
3. %   Generate part Fourier matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   Phi -- The part Fourier matrix  
7.   
8. %% Generate part Fourier matrix     
9.     Phi_t = fft(eye(N,N))/sqrt(N);%Fourier matrix  
10.     RowIndex = randperm(N);  
11.     Phi = Phi_t(RowIndex(1:M),:);%Select M rows randomly  
12.     %normalization  
13.     for ii = 1:N  
14.         Phi(:,ii) = Phi(:,ii)/norm(Phi(:,ii));  
15.     end  
16. end  

5、稀疏随机矩阵

[plain]  view plain  copy

1. function [ Phi ] = SparseRandomMtx( M,N,d )  
2. %SparseRandomMtx Summary of this function goes here  
3. %   Generate SparseRandom matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   d -- The number of '1' in every column,d<M   
7. %   Phi -- The SparseRandom matrix  
8.   
9. %% Generate SparseRandom matrix     
10.     Phi = zeros(M,N);  
11.     for ii = 1:N  
12.         ColIdx = randperm(M);  
13.         Phi(ColIdx(1:d),ii) = 1;  
14.     end  
15. end  

6、托普利兹矩阵和循环矩阵

        这里先给出托普利兹矩阵，文中说经过M次循环，这里直接利用MATLAB自带函数生成一个托普利兹方阵再取前M行。

[plain]  view plain  copy

1. function [ Phi ] = ToeplitzMtx( M,N )  
2. %ToeplitzMtx Summary of this function goes here  
3. %   Generate Toeplitz matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   Phi -- The Toeplitz matrix  
7.   
8. %% Generate a random vector  
9. %     %(1)Gauss  
10. %     u = randn(1,2*N-1);  
11.     %(2)Bernoulli  
12.     u = randi([0,1],1,2*N-1);  
13.     u(u==0) = -1;  
14. %% Generate Toeplitz matrix     
15.     Phi_t = toeplitz(u(N:end),fliplr(u(1:N)));  
16.     Phi = Phi_t(1:M,:);  
17. end  

        下面是循环矩阵，仍然利用MATLAB自带函数生成。

[plain]  view plain  copy

1. function [ Phi ] = CirculantMtx( M,N )  
2. %CirculantMtx Summary of this function goes here  
3. %   Generate Circulant matrix   
4. %   M -- RowNumber  
5. %   N -- ColumnNumber  
6. %   Phi -- The Circulant matrix  
7.   
8. %% Generate a random vector  
9. %     %(1)Gauss  
10. %     u = randn(1,N);  
11.     %(2)Bernoulli  
12.     u = randi([0,1],1,N);  
13.     u(u==0) = -1;  
14. %% Generate Circulant matrix     
15.     Phi_t = toeplitz(circshift(u,[1,1]),fliplr(u(1:N)));  
16.     Phi = Phi_t(1:M,:);  
17. end  

        以上都是采用MATLAB自带的toeplitz函数，这需要首先生成一个随机向量，而托普利兹矩阵和循环矩阵的区别也就在于这个随机向量的结构不同，注意代码中有关toeplitz函数的两个输入参数好好体会即可。