-
Sigmoid函数
特征:
范围[-1,1],历史上很受欢迎。
缺点:
容易产生梯度消失的问题。
输出不是以0为中心。容易产生锯齿现象。
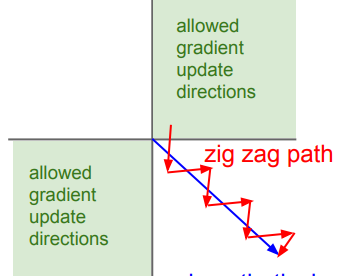
指数计算量大。
-
tanh函数
特点:
将数字加到范围[-1,1]
以零为中心(不错)
饱和时仍然会杀死梯度(因为tanh求导后,在饱和时梯度近似为0)
指数计算量大
-
ReLU(修正线性单元)
特点:
非常计算效率高,没有指数和正切的计算
收敛速度比Sigmoid / tanh快
不存在梯度消失的问题
在计算过程中,一半神经元在计算过程中为0,计算效率更高,而且自然的形成了"稀疏表示",用少量的神经元可以高效灵活稳健的表示抽象复杂的概念。但是学习率选择不好,导致网络死去。
也不是以0位中心
-
Leaky ReLU
特征:
不饱和
计算效率高
收敛速度比sigmoid / tanh快!
不会杀"死"网络
-
PReLU
-
MaxOut
特点:
没有固定的形式
可以生成ReLU和LReLU
线性,不饱和,不杀死网络。
网络结构参数多。
-
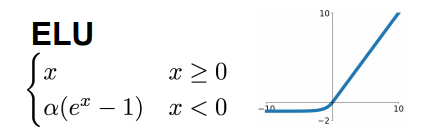
ELU
特点:
具有ReLU的所有好处
更接近于零平均输出
负饱和状态
与Leaky ReLU相比增加了一些鲁棒性,对抗噪声。
需要计算指数







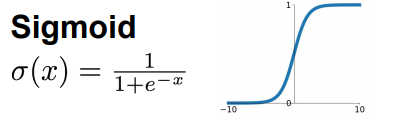
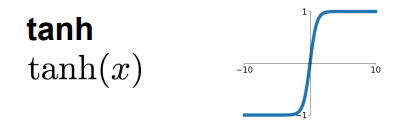


















 3178
3178

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








