POJ 3666 Making the Grade [DP]

题意：

给定一个序列，以最小代价将其变成单调不增或单调不减序列，这里的代价看题目公式。

思路：

很容易想到是DP。

1.

对前i个序列，构成的最优解其实就是与两个参数有关。一个是这个序列处理后的最大值mx，和这个序列处理的代价值cost。

显然最大值mx最小最好（这样第i+1个值可以不花代价直接接在其后面的可能性更大），cost最小也最好（题意要求），但是两者往往是鱼和熊掌。

用dp[i][j]表示：前i个数构成的序列，这个序列最大值为j，dp[i][j]的值代表相应的cost。

所以状态转移方程如下：

dp[i][j]=abs(j-w[i])+min(dp[i-1][k]);(k<=j)

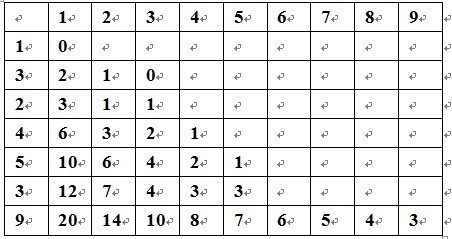
这个表格是根据转移方程写出来的dp数组。

再仔细看一下转移方程：dp[i][j]=abs(j-w[i])+min(dp[i-1][k]);(k<=j)

右边没填充的是因为填充的数字肯定比前面的数字大，无用，因为在求min( dp[i-1][k] )时，是求最小值，既然更大，则最小值时无需考虑。

又从表格中可以看出：

dp[i][j]=abs(j-w[i])+min(dp[i-1][k]);(k<=j)这里的k无需从1遍历到j。

只要在对j进行for循环的时候不断更新一个dp[i-1][j]的最小值mn=min（mn,dp[i-1][j]），

然后对dp[i][j]=abs(j-w[i])+mn即可;

这样改进之后即可从本来的时候时间复杂度O(NMM)改进为O(NM);

但是，这里的m是A[i]的最大值,显然TLE。

所以必须用离散化思想改进，因为N=2000。远小于A[i]的最大值。

离散化：将序列排序一下，然后用位置的前后关系来制定其值，这样时间复杂度变成O(N^2).

最后是这题数据有bug，只需要求不减序列即可。

#include <iostream>
#include <cmath>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
long long n;
long long a[2222];
long long b[2222];
long long dp[2222][2222];
long long Abs(long long a,long long b)
{
	return a>b?a-b:b-a;
}
void solve()
{
	long long minn=(1<<30);
	for(long long i=1;i<=n;i++)
	{
		minn=dp[i-1][1];
		for(long long j=1;j<=n;j++)
		{
			minn=min(minn,dp[i-1][j]);
			dp[i][j]=minn+Abs(a[i],b[j]);
		}
	}
	long long ans=0x7fffffffffffffffL;
	for(int i=1;i<=n;i++)
	{
		ans=min(ans,dp[n][i]);
	}
	printf("%lld\n",ans);
}
int main()
{
    //freopen("/home/rainto96/in.txt","r",stdin);
	scanf("%lld",&n);
	for(long long i=1;i<=n;i++)
	{
		scanf("%lld",a+i);
		b[i]=a[i];
	}
	sort(b+1,b+1+n);
	solve();
	return 0;
}