【题目描述】
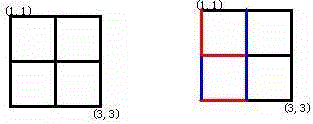
Alice和Bob玩了一个古老的游戏:首先画一个n × n的点阵(下图n = 3)
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
直到围成一个封闭的圈(面积不必为1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了(n ≤ 200),他们的游戏实在是太长了!他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序,帮助他们计算他们是否结束了游戏?
【输入】
输入数据第一行为两个整数n和m。m表示一共画了m条线。以后m行,每行首先有两个数字(x, y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是"D ",则是向下连一条边,如果是"R "就是向右连一条边。输入数据不会有重复的边且保证正确。
【输出】
输出一行:在第几步的时候结束。假如m步之后也没有结束,则输出一行“draw”。
【输入样例】
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D【输出样例】
4
【源程序】
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 1000001
#define MOD 123
#define E 1e-6
using namespace std;
struct Node{
int x;
int y;
}father[210][210],a,b;
Node Find(Node temp)
{
if(father[temp.x][temp.y].x==temp.x&&father[temp.x][temp.y].y==temp.y)
return temp;
return father[temp.x][temp.y]=Find(father[temp.x][temp.y]);
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
father[i][j].x=i;
father[i][j].y=j;
}
for(int i=1;i<=m;i++)
{
int x,y;
char ch[10];
cin>>x>>y>>ch;
if(ch[0]=='D')
{
a=Find(father[x][y]);
b=Find(father[x+1][y]);
}
else if(ch[0]=='R')
{
a=Find(father[x][y]);
b=Find(father[x][y+1]);
}
if(a.x==b.x&&a.y==b.y)
{
cout<<i<<endl;
return 0;
}
else
father[b.x][b.y]=a;
}
cout<<"draw"<<endl;
return 0;
}







 本文介绍了一种用于检测两人轮流在点阵中画线游戏何时结束的算法。通过并查集的方法,判断玩家画线形成封闭区域时的具体步骤,实现游戏胜负的自动判定。
本文介绍了一种用于检测两人轮流在点阵中画线游戏何时结束的算法。通过并查集的方法,判断玩家画线形成封闭区域时的具体步骤,实现游戏胜负的自动判定。
















 316
316

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








