图论 —— 生成树 —— 最小生成树 —— Prim

本文链接：https://blog.csdn.net/u011815404/article/details/88625323

【基本思想】

Prim 算法基本思想是蓝白点思想，用白点代表已进入最小生成树的点，蓝点代表未进入最小生成树的点。

每次循环都将一个蓝点 u 变为白点，并且此蓝点 u 与白点相连的最小边权 min[u] 还是当前所有蓝点中最小的。这相当于每次循环让一个新的点加入生成树，让一条最小边加入生成树，n-1 次循环就能生成一棵含有 n 个点的树，最后得到的一定是最小生成树。

其时间复杂度为：O（N*N），N 代表点数。

【算法分析】

以下图为例，蓝点和虚线代表未进入最小生成树的点、边，白点和实现代表已进入最小生成树是点、边。

初始时，所有点都是蓝点，min[1]=0，min[2、3、4、5]=INF，权值和 MST=0。

第一次循环找到 min[1]=0 最小的蓝点 1。将 1 变为白点，接着枚举与 1 相连的所有蓝点 2、3、4，修改它们与白点相连的最小边权。故有：min[2]=w[1][2]=2，min[3]=w[1][3]=4，min[4]=w[1][4]=7，MST=0。

第二次循环是找到 min[2] 最小的蓝点 2。将 2 变为白点，接着枚举与 2 相连的所有蓝点 3、5，修改它们与白点相连的最小边权。故有：min[3]=w[2][3]=1，min[5]=w[2][5]=2，MST=2。

第三次循环是找到 min[3] 最小的蓝点 3。将 3 变为蓝点，接着枚举与 3 相邻的所有蓝点 4、5，修改它们与白点相连的最小边权。故有：min[4]=w[3][4]=1，由于 min[5]=2<w[3][5]=6，所以不修改 min[5] 的值，MST=3。

最后两轮循环将点 4、5 以及边 w[2][5]、w[3][4] 添加进最小生成树。

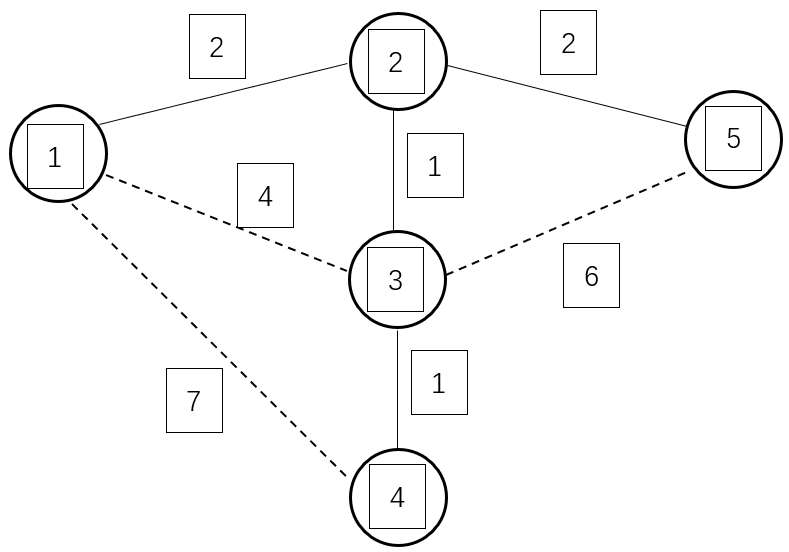
最后权值之和 MST=6。

【算法描述】

以 1 为起点生成最小生成树，vis[v] 代表 v 点是否加入最小生成树中，min[v] 代表蓝点 v 与白点相连的最小边权，MST 代表最小生成树边权之和。

初始化：

vis[1...n]=false，MST=0

min[v]=INF（v≠1），min[1]=0

主体

void Prim()
{
    for(int i=1;i<=n;i++)
    {
        int u=0;
    
        for(int j=1;j<=n;j++)//枚举所有点
            if( vis[j]==false && min[j]<min[u])//寻找与白点相连的权值最小的蓝点u
                u=j;
        vis[u]=true;//蓝点u加入生成树，标记为白点
    
        for(int j=1;j<=n;j++)//修改所有与u相连的蓝点
        	if( vis[j]==false && g[u][j]<min[j] )
                min[j]=g[u][j];
    }

    //权值和的计算
    int MST=0;
    for(int i=1;i<=n;i++)
        MST+=min[i];
}

【模版】

int n,m;//n个点m条边
int G[N][N];
int dis[N];
bool vis[N];
int MST;
void Prim(){
    for(int i=1;i<=n;i++){
        int k;
        int minn=INF;
        for(int j=1;j<=n;j++){//枚举所有点
            if(!vis[j]&&dis[j]<minn){//寻找与白点相连的权值最小的蓝点u
                minn=dis[j];
                k=j;
            }
        }
        vis[k]=true;//蓝点u加入生成树，标记为白点
        for(int j=1;j<=n;j++)//修改所有与u相连的蓝点
            if(!vis[j]&&dis[j]>G[k][j])
                dis[j]=G[k][j];
    }

    MST=0;
    for(int i=1;i<=n;i++)//权值和的计算
        MST+=dis[i];
}

int main(){
    cin>>n>>m;
    memset(vis,false,sizeof(vis));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>G[i][j];
    for(int i=1;i<=n;i++)
        dis[i]=G[1][i];
    Prim();
    cout<<MST<<endl;
    return 0;
}