系统传递函数的理解

最近复习了一下大学时的信号系统，感觉有了新的体会，故而记下笔记。

大部分系统可以用线性常微分方程建模，即

其中是系统输入，是系统输出。通过拉氏变换，可以整理得到有理化系统传递函数，即

通常有理化系统传递函数可以拆分为多个一阶系统传递函数、二阶系统传递函数的组合，因此研究一阶系统传递函数和二阶系统传递函数很有意义。

1. 一阶系统传递函数的单位冲击响应为，因此为了使系统稳定，那么使单位冲激响应是衰减函数(绝对可积)。把复平面上成为一阶系统传递函数的极点。
2. 二阶系统传递函数的单位冲激响应为，因此为了使系统稳定，与一阶系统相似，需要满足，即当时，二阶系统传递函数有两个不同的实数极点，当时，二阶系统传递函数有两个相同的实数极点，而当时，二阶系统传递函数有两个共轭的复数极点。成为阻尼系数，当时称为过阻尼，表现为系统响应无震荡但是响应速度慢；当时称为欠阻尼，表现为系统响应速度快但是震荡；当时称为临界阻尼，表现为系统响应速度快且无震荡；不同阻尼系数对系统响应的影响如下图所示，

   

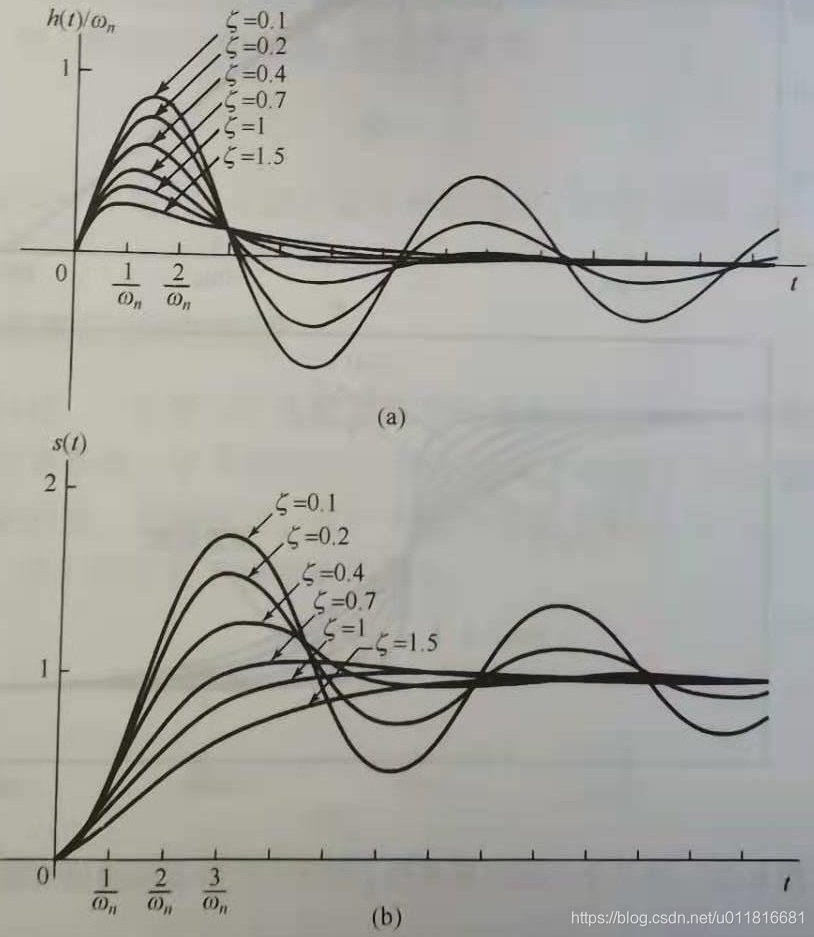
   不同阻尼系数的二阶系统响应

   从常微分方程到有理化传递函数变换过程中可以发现，系统传递函数的极点反映了系统本身的特性，与输入激励特征无关。相当于微分方程的通解，在信号与系统中成为本征模态。极点对应的单位冲激响应就把系统特性与系统传递函数的极点联系起来了。