针对基础蝗虫优化算法的局部探索与全局搜索能力不平衡的问题，提出了混合柯西变异和均匀分布的蝗虫优化算法(HCUGOA)。HCUGOA采用非线性递减的控制参数c，增强全局探索；结合柯西算子与分段思想更新策略，提高跳出局部最优的能力；同时融合柯西变异和反向学习策略更新目标位置，优化算法性能。实验结果表明，HCUGOA在多个测试函数中表现出更好的寻优效果和收敛速度。
混合柯西变异和均匀分布的蝗虫优化算法
文章目录
摘要：由于位置更新公式存在的局部开发能力较强而全局探索能力较弱的缺陷, 导致蝗虫优化算法 (GOA) 易陷入局部最优, 易早熟收敛. 因此提出混合柯西变异和均匀分布的蝗虫优化算法 (HCUGOA), 受柯西算子和粒子群算法的启发, 提出具有分段思想的位置更新方式以增加种群多样性, 增强全局探索能力; 将柯西变异算子和反向学习策略相融合, 对最优位置即目标值进行变异更新, 提高算法跳出局部最优的能力; 为了更好的平衡全局探索和局部开发, 将均匀分布函数引入到非线性控制参数 c, 构建新的随机调整策略.
1.蝗虫优化算法
基础蝗虫优化算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107694862
2. HCUGOA 算法
2.1 服从均匀分布随机调整策略
GOA 的控制参数 c 是协调探索和开发的关键,c 是随着迭代次数动态变化的, 且是线性递减函数, 在搜索过程中难以适应优化的实际情况: 在迭代前期参数 c 下降过快易导致蝗虫不能遍历更多搜索空间, 最终导致全局探索不足; 在迭代后期c 下降过慢, 会导致局部开发受限, 收敛速度慢. 为解决这一问题, 并重新构建新函数 c(t):
c
(
t
)
=
δ
(
lg
(
c
max
T
max
)
−
20
t
+
exp
(
t
T
max
)
−
20
(
c
max
−
c
min
)
)
(4)
c(t)=\delta\left(\lg \left(\frac{c_{\max }}{T_{\max }}\right)^{-20 t}+\exp \left(\frac{t}{T_{\max }}\right)^{-20\left(c_{\max }-c_{\min }\right)}\right) \tag{4}
c(t)=δ(lg(Tmaxcmax)−20t+exp(Tmaxt)−20(cmax−cmin))(4)
其中
δ
δ
δ 是服从
[
0
,
T
m
a
x
]
[0,T_{max} ]
[0,Tmax] 之间均匀分布的随机数,且
δ
δ
δ的取值范围介于 0 到 1 之间.
由式 (4) 可知, c(t) 是非线性递减函数,c(t) 随迭代次数增加在迭代期间呈非线性状态减小, 具体表现为在前期函数下降缓慢, 给全局探索充分时间, 后期函数迅速下降收敛,加快算法收敛速度;同时,引入服从均匀分布随机数 δ, 前期让参数 c 有可能继续保持较大值, 一定程度上加强全局搜索; 后期参数 c 随着迭代次数增加而减小, 且变化比较缓慢, 此时服从均匀分布的随机数可能产生较大的值让参数 c 实现动态变化, 从而加快算法开发和收敛速度.
2.2 结合柯西算子和分段思想的更新策略
基本 GOA 位置更新由自身位置与其他所有蝗虫间交互力及目标位置决定, 因此GOA 具有很强的局部开发能力而全局探索能力不足. 为更好地提升算法性能, 本节对算法进行分段处理.
在算法搜索前半段, 受 PSO 对每代最优解进行记忆保存的思想启发, 对式 (2) 进行改进:
X
n
e
w
(
t
+
1
)
=
b
1
∗
W
+
b
2
∗
r
1
(
X
b
e
s
t
(
t
)
−
X
i
(
t
)
)
+
b
2
∗
r
2
(
X
j
(
t
)
−
X
k
(
t
)
)
(5)
\begin{aligned} X_{n e w}(t+1) &=b 1 * W+b 2 * r 1\left(X_{b e s t}(t)-X_{i}(t)\right)+b 2 * r 2\left(X_{j}(t)-X_{k}(t)\right) \end{aligned} \tag{5}
Xnew(t+1)=b1∗W+b2∗r1(Xbest(t)−Xi(t))+b2∗r2(Xj(t)−Xk(t))(5)
其中
X
n
e
w
(
t
+
1
)
X_{n e w}(t+1)
Xnew(t+1) 是第
i
i
i只蝗虫在第
t
+
1
t + 1
t+1 代的位置,
X
b
e
s
t
(
t
)
X_{b e s t}(t)
Xbest(t)是第
t
t
t 代最优位置,
X
i
(
t
)
X_i(t)
Xi(t) 是第
i
i
i只蝗虫在第
t
t
t 代的位置,
X
j
(
t
)
X_j (t)
Xj(t) 和
X
k
(
t
)
X_k (t)
Xk(t) 是第
t
t
t 代两个随机位置,
r
1
r_1
r1 和
r
2
r_2
r2 分别为区间 [0,1] 内产生的随机数,
b
1
b_1
b1 是记忆系数,
b
2
b_2
b2 是信息交流系数:
b
1
=
exp
(
c
(
t
)
−
30
t
T
max
)
−
t
(6)
b 1=\exp \left(c(t)-30 \frac{t}{T_{\max }}\right)^{-t} \tag{6}
b1=exp(c(t)−30Tmaxt)−t(6)
b 2 = ( T max − t T max ) N (7) b 2=\left(\frac{T_{\max }-t}{T_{\max }}\right)^{N} \tag{7} b2=(TmaxTmax−t)N(7)
其中 W 是与所有蝗虫相互联系决定位置更新的步长函数,
W
=
∑
j
=
1
,
j
≠
i
N
c
(
t
)
u
b
d
−
l
b
d
2
s
(
∣
x
j
d
−
x
i
d
∣
)
x
j
−
x
i
d
j
(8)
W=\sum_{j=1,j\neq i}^Nc(t)\frac{ub_d-lb_d}{2}s(|x_j^d-x_i^d|)\frac{x_j-x_i}{d_j}\tag{8}
W=j=1,j=i∑Nc(t)2ubd−lbds(∣xjd−xid∣)djxj−xi(8)
与式 (2) 相比, 式 (5) 分为 3 个部分:1) 利用除最优解外的全部位置信息, 有助于个体间进行信息交互, 增强全局探索能力;2) 由自身位置和最优位置决定, 加强算法开发能力和收敛速度;3) 通过随机选择两个个体引导位置更新, 增强全局探索能力.
在算法搜索后半段, 引入柯西算子作为变异步长, 当个体陷入局部最优时, 较大的步长可帮助个体跳出局部极值; 当个体接近收敛, 并在搜索最优解时,较小步长可加速个体的收敛, 公式如下:
X
i
d
(
t
+
1
)
=
X
i
d
(
t
)
+
Cauchy
⊕
(
X
b
e
s
t
d
(
t
)
−
X
k
d
(
t
)
)
(9)
X_{i}^{d}(t+1)=X_{i}^{d}(t)+\text { Cauchy } \oplus\left(X_{b e s t}^{d}(t)-X_{k}^{d}(t)\right) \tag{9}
Xid(t+1)=Xid(t)+ Cauchy ⊕(Xbestd(t)−Xkd(t))(9)
其中
X
k
d
X_{k}^{d}
Xkd是随机选择的第
k
k
k只蝗虫在第
d
d
d维的位置,Cauchy 是柯西算子, 一维标准的柯西分布的概率密度函数表达式如下:
f
(
x
)
=
1
π
(
1
x
2
+
1
)
,
−
∞
<
x
<
∞
(10)
f(x)=\frac{1}{\pi}\left(\frac{1}{x^{2}+1}\right),-\infty<x<\infty \tag{10}
f(x)=π1(x2+11),−∞<x<∞(10)
判断算法是进行前半段探索还是后半段开发由控制概率
P
c
P_c
Pc 决定,
P
c
P_c
Pc 的表示为:
P
c
=
1
2
T
max
(11)
P_{c}=\frac{1}{2} \mathrm{~T}_{\max } \tag{11}
Pc=21 Tmax(11)
算法前期需进行大范围全局探索, 后期需进行小范围的局部开发并避免算法过早收敛, 所以对位置更新引入分段思想, 前期对最优解进行记忆保存,加强全局寻优能力, 并引入记忆系数和交流系数, 通过个体自身位置、最优位置及两个随机位置共同决定新位置; 后期引入柯西算子, 一定程度上降低算法陷入局部最优概率, 并加快算法的收敛速度.
算法 1 结合柯西算子和分段思想的策略
1)if rand< P c
2)根据式 (5)∼(8) 更新个体位置;
3)else
4)根据式 (9) 和 (10) 更新个体位置;
5)end
2.3 融合柯西变异和反向学习策略
基本 GOA 中, 目标位置更新依赖于每次迭代后的位置更新, 重新计算适应度, 选择最优位置对目标位置进行取代, 未对目标位置进行主动的扰动更新,导致算法易陷入局部最优. 所以, 本节融合柯西变异和反向学习策略, 依概率对目标位置进行随机扰动
更新, 避免算法陷入局部最优.
反向学习是 Tizhoosh 在 05 年提出的新技术,目的是基于当前解, 寻到其对应反向解, 通过评估选择保存更好的解. 为更好的引导个体寻到最优解, 将反向学习融入 GOA 中, 数学描述如下:
X
b
e
s
t
∗
(
t
)
=
u
b
+
r
⊕
(
l
b
−
X
b
e
s
t
(
t
)
)
(12)
X_{b e s t}^{*}(t)=u b+r \oplus\left(l b-X_{b e s t}(t)\right) \tag{12}
Xbest∗(t)=ub+r⊕(lb−Xbest(t))(12)
X n e w ( t + 1 ) = b 3 ⊕ ( X b e s t ( t ) − X b e s t ∗ ( t ) ) (13) X_{n e w}(t+1)=b 3 \oplus\left(X_{b e s t}(t)-X_{b e s t}^{*}(t)\right)\tag{13} Xnew(t+1)=b3⊕(Xbest(t)−Xbest∗(t))(13)
其中
X
n
e
w
∗
(
t
)
X_{n e w}^*(t)
Xnew∗(t) 是第
t
t
t 代目标解
X
b
e
s
t
X_{best}
Xbest的反向解,
X
n
e
w
(
t
+
1
)
X_{n e w}(t+1)
Xnew(t+1)是第
t
+
1
t + 1
t+1代目标解,
u
b
ub
ub 和
l
b
lb
lb 是上下界,
r
r
r是服从 (0,1) 标准均匀分布 1×dim 的随机数矩阵(其中dim表算法搜索空间维数),
b
3
b_3
b3是伪信息交流系数, 表达式如下:
b
3
=
(
T
max
−
t
T
max
)
t
(14)
b 3=\left(\frac{T_{\max }-t}{T_{\max }}\right)^{t} \tag{14}
b3=(TmaxTmax−t)t(14)
将柯西算子引入目标位置更新, 发挥柯西算子的调节能力, 增强算法跳出局部最优的能力:
X
n
e
w
(
t
+
1
)
=
cauch
y
⊕
X
best
(
t
)
(15)
X_{n e w}(t+1)=\operatorname{cauch} y \oplus X_{\text {best }}(t) \tag{15}
Xnew(t+1)=cauchy⊕Xbest (t)(15)
为提高算法寻优性能, 将反向学习策略和柯西算子扰动策略在一定概率下交替执行, 动态的随机更新目标位置. 反向学习策略中, 通过一般反向学习策略得到反向解,增大算法搜索范围,同时,式(12)中的上下界 ub 和 lb 是动态变化的, 相对于固定边界的策略更利于算法优化; 柯西变异策略中运用变异算子对最优位置进行变异产生新解, 一定程度上改善算法易陷入局部最优的缺陷. 决定选择何种策略进行更新的选择概率
P
s
Ps
Ps 定义如下:
P
s
=
−
exp
(
1
−
t
T
max
)
20
+
θ
(16)
P_{s}=-\exp \left(1-\frac{t}{T_{\max }}\right)^{20}+\theta \tag{16}
Ps=−exp(1−Tmaxt)20+θ(16)
其中θ 为调节因子,经多次实验,θ 取值为0.05时函数优化结果最优.
算法 2 融合柯西变异和反向学习策略
1)if rand< P s
2)根据式 (12)∼(14) 反向学习策略更新目标位
置;
3)else
4)根据公式 (15) 柯西变异策略更新目标位置;
5)end
对目标位置进行扰动更新虽能让算法跳出局部最优, 但不能保证新位置优于原目标位置, 因此在扰动更新操作后加入贪婪机制, 通过比较新旧目标位置的适应度后再决定是否更新目标位置.
算法 3 贪婪算法
1)if
f
(
X
n
e
w
)
<
f
(
X
b
e
s
t
)
f(X_{new} ) < f(X_{best} )
f(Xnew)<f(Xbest)
2)
X
b
e
s
t
=
X
n
e
w
X_{best} = X_{new}
Xbest=Xnew ;
3)else
4)
X
b
e
s
t
=
X
b
e
s
t
X_{best} = X_{best}
Xbest=Xbest
5)end
基于贪婪选择策略促进算法向着期望寻找到的目标位置方向进化, 让目标位置能够充分发挥引导作用, 使算法获得更好的收敛速度和精度.
算法流程图如下：
3.实验结果
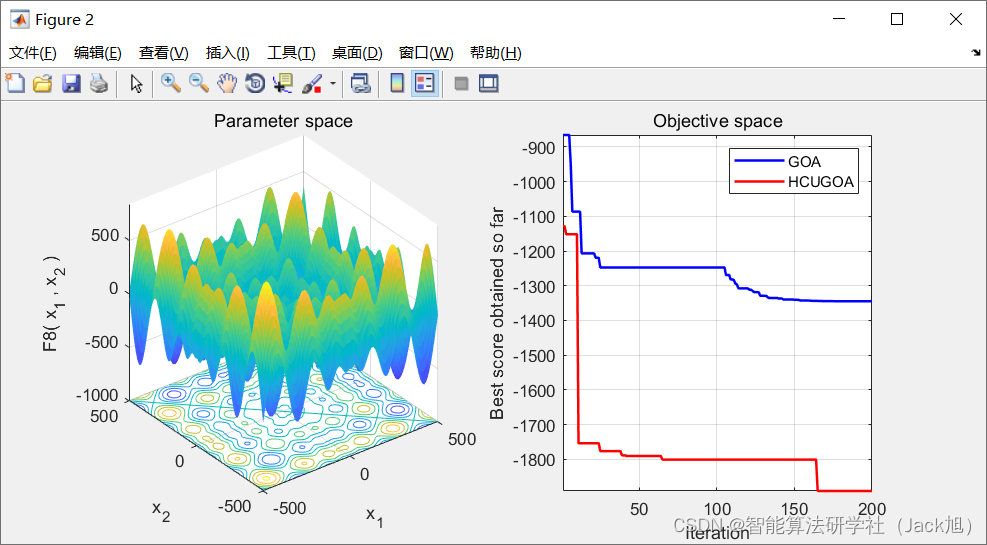
4.参考文献
[1]何庆,林杰,徐航.混合柯西变异和均匀分布的蝗虫优化算法[J/OL].控制与决策:1-10[2021-01-08].https://doi.org/10.13195/j.kzyjc.2019.1609.
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
