图解图论介绍及应用（6）：图算法介绍

最新推荐文章于 2024-07-22 21:17:59 发布

ronghuaiyang

最新推荐文章于 2024-07-22 21:17:59 发布

阅读量746

点赞数

本文链接：https://blog.csdn.net/u011984148/article/details/99440296

版权

点击上方“AI公园”，关注公众号，选择加“星标“或“置顶”

作者：Vardan Grigoryan

编译：ronghuaiyang

导读

知识图谱是AI领域非常有用的一种工具，知识图谱的基础就是图论，从今天开始，给大家介绍一些图论的基础内容，今天是第6篇，图算法的介绍。昨天应该是第5篇，写错了，不好意思。

使用图进行的任何处理都可以归类为“图算法”。你可以实现一个函数打印一个图的所有顶点，并命名为“<张三>的顶点打印算法”。我们大多数人都害怕教科书中列出的图算法(参见这里的完整列表)(https://en.wikipedia.org/wiki/Listofalgorithms#Graph_algorithms)。让我们试着应用一个二分图匹配算法，比如Hopcroft-Karp算法来解决Airbnb的房屋过滤问题：

给出Airbnb homes (H)和filters (F)的二分图，其中H的每个元素(顶点)可以有多个F的相邻元素(顶点)(共享一条公共边)。找到H的一个子集，它由F的一个子集中与顶点相邻的顶点组成。

混淆问题的定义，但我们不能确定在这一点上是否Hopcroft-Karp算法能解决我们的问题。但我向你们保证，这段旅程将教会我们许多图算法背后的关键思想。旅程并不短，所以要有耐心。

Hopcroft-Karp算法是用来解决二分图最大匹配问题的一种算法。为了降低时间复杂度，在Hopcroft-Karp算法中，我们在增加匹配集合M时，每次寻找多条增广路径。

熟悉此算法的读者已经知道，这并不能解决我们的问题，因为匹配要求没有两条边共享一个公共顶点。

让我们看一个例子，其中只有4个过滤器和8个home(为了简单起见)。

home由字母A到H表示，过滤器随机选择。
A房子价格(50美元)和有一张床(这是我们的全部价格)。
从A到H的所有家庭都有每晚50美元的价格标签和一张床，但很少有“Wi-Fi”和/或“电视”。

因此，下面的插图试图展示我们应该“返回”哪些home来响应请求，要求提供所有四个过滤器(例如，每晚50美元，有一张床，还有Wi-Fi和电视)。

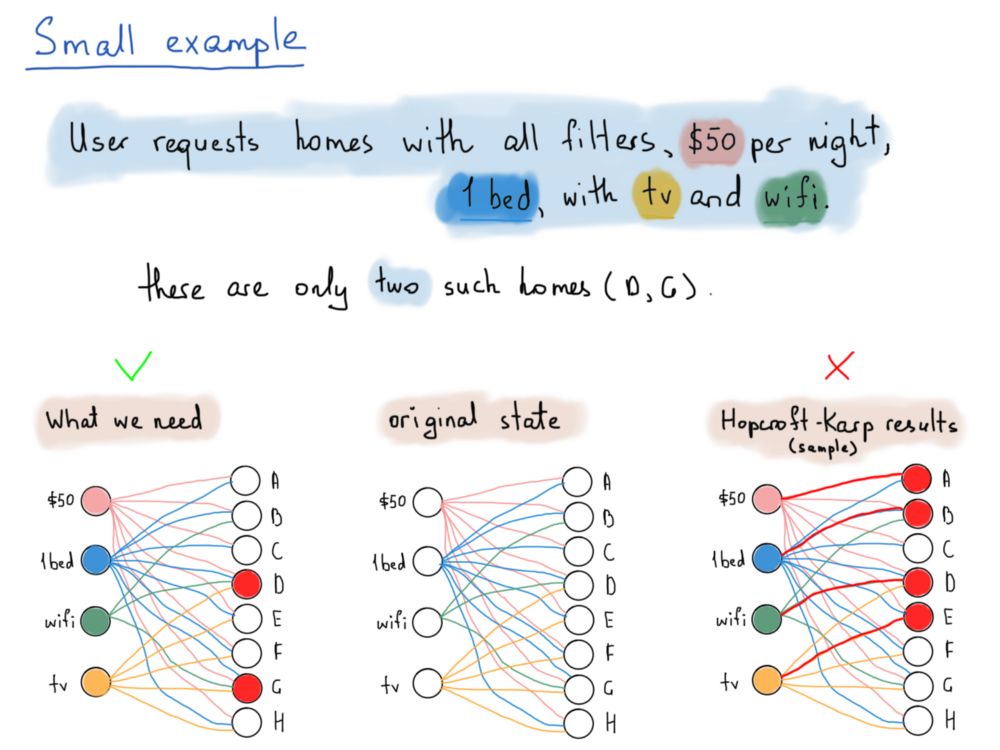
640?wx_fmt=png

我们的问题的解决方案要求具有公共顶点的边导致不同的主顶点，这些主顶点与相同的过滤器子集相关联，而Hopcroft-Karp算法消除了具有公共端点的边，并在两个子集中生成与顶点相关联的边。

看看上面的插图，我们只需要home D和G，它们都满足所有四个过滤器值。我们真正需要的是得到所有共享一个公共端点的匹配边。

我们可以为这种方法设计一种算法，但是它的处理时间与用户需求无关(用户需求=闪电般的速度，就在这里，就在现在)。创建一个包含多个排序键的平衡二叉搜索树可能会更快，就像一个数据库索引文件一样，它用一组令人满意的记录映射主键/外键。

平衡二叉搜索树和数据库索引将在另一篇文章中讨论，我们将再次回到Airbnb家庭过滤问题。

Hopcroft-Karp算法(以及许多其他算法)基于DFS(深度优先搜索)和BFS(宽度优先搜索)图遍历算法。老实说，在这里引入Hopcroft-Karp算法的真正原因是偷偷地切换到图遍历，最好从漂亮的图(二叉树)开始。

二叉树遍历非常漂亮，主要是因为它们是递归的。有三种基本的遍历称为顺序遍历、后顺序遍历和前序遍历(你可以使用自己的遍历算法)。如果你曾经遍历过链表，那么它们很容易理解。在链表中，你只需打印当前节点的值(在下面的代码中名为“item”)，然后继续到下一个节点。

// struct ListNode {	
//   ListNode* next;	
//   T item;	
// };	
void TraverseRecursive(ListNode* node) // starting node, most commonly the list 'head'	
{	
  if (!node) return; // stop	
  std::cout << node->item;	
  TraverseRecursive(node->next); // recursive call	
}	
void TraverseIterative(ListNode* node)	
{	
  while (node) {	
    std::cout << node->item;	
    node = node->next;	
  }	
}

对于二叉树也几乎是一样的，你打印节点值(或者你需要对它做的任何其他事情)，然后继续到下一个节点，但是在本例中，有“两个下一个”节点，左边和右边。因此，你应该对左右节点执行相同的操作。但你有三个不同的选择：

打印节点值，然后转到左侧节点，然后转到右侧节点，或者
转到左节点，打印节点值，然后转到右节点，或
转到左节点，然后转到右节点，然后打印节点的值。

// struct TreeNode {	
//   T item;	
//   TreeNode* left;	
//   TreeNode* right;	
// }	
// you cann pass a callback function to do whatever you want to do with the node's value	
// in this particular example we are just printing its value.	
// node is the "starting point", basically the first call is done with the "root" node	
void PreOrderTraverse(TreeNode* node)	
{	
  if (!node) return; // stop	
  std::cout << node->item;	
  PreOrderTraverse(node->left); // do the same for the left sub-tree	
  PreOrderTraverse(node->right); // do the same for the right sub-tree	
}	
void InOrderTraverse(TreeNode* node)	
{	
  if (!node) return; // stop	
  InOrderTraverse(node->left);	
  std::cout << node->item;	
  InOrderTraverse(node->right);	
}	
void PostOrderTraverse(TreeNode* node)	
{	
  if (!node) return; // stop	
  PostOrderTraverse(node->left);	
  PostOrderTraverse(node->right);	
  std::cout << node->item;	
}

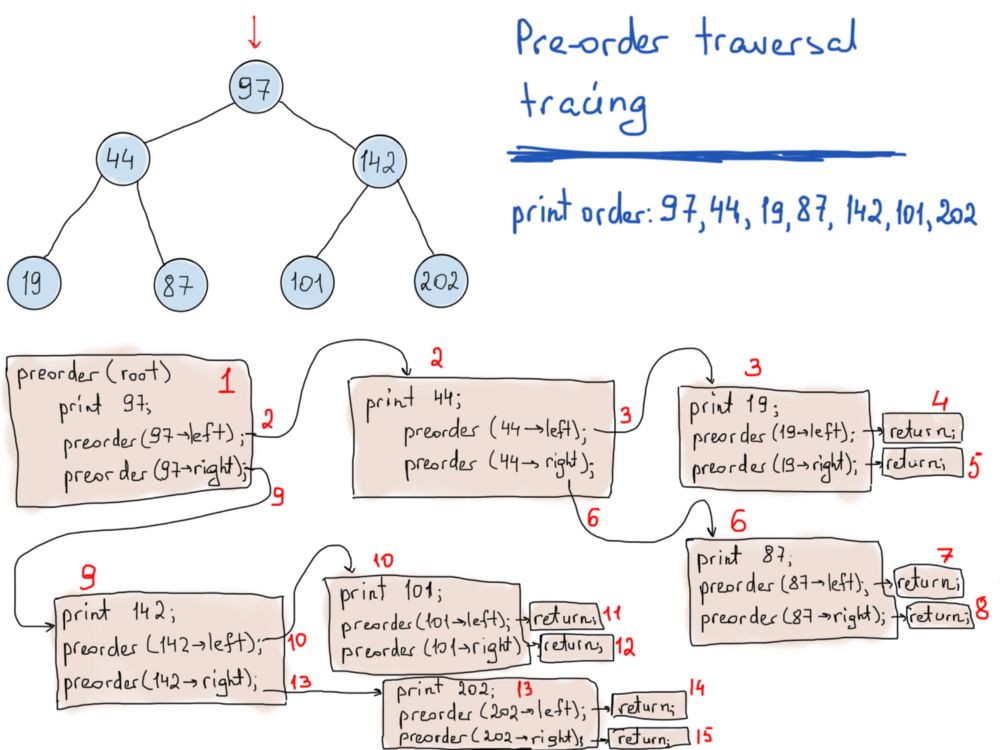
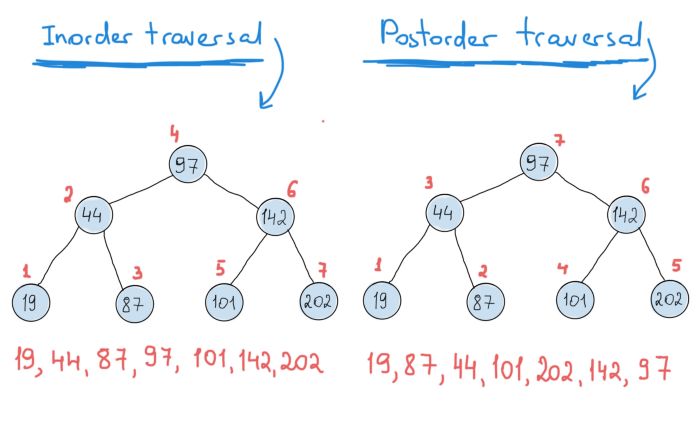
640?wx_fmt=png

预遍历的详细跟踪

640?wx_fmt=png

显然，递归函数看起来非常优雅，尽管它们非常昂贵。每次我们递归地调用一个函数，这意味着我们调用一个完全“新的”函数(见上图)。这里的“new”是指应该为函数参数和局部变量“分配”另一个堆栈内存空间。这就是递归调用代价高昂(额外的堆栈空间分配和许多函数调用)和危险(注意堆栈溢出)的原因，显然建议使用迭代实现。在关键任务系统编程中(飞机、NASA漫游车等等)，递归是完全禁止的(没有统计数据，没有经验，只是告诉你谣言)。

（未完待续）