【机器学习－西瓜书】三、线性回归；对数线性回归

最新推荐文章于 2024-09-18 16:49:32 发布

TensorSense

最新推荐文章于 2024-09-18 16:49:32 发布

阅读量1.5w

点赞数 4

分类专栏： machine learning 文章标签：机器学习线性回归

本文链接：https://blog.csdn.net/u011995719/article/details/77526943

版权

machine learning 专栏收录该内容

21 篇文章 18 订阅

订阅专栏

墙裂推荐阅读：ｙ的衍生物

关键词：最小二乘法；正则化；对数线性回归； y的衍生物

3.1 基本形式

假设样本x有d个属性，线性模型（linear model）试图学得一个通过属性的线性组合来进行预测的函数，即 $f(x)=w_{1}x_{1} + w_{2}x_{2}+\cdot \cdots +w_{d}x_{d}+b$ ，向量形式 $f(x)=w^{T}x+b$

3.2 线性回归

关键词：无序属性连续化。
对离散属性，若属性值之间存在“序”（order）关系，可通过连续化将其转化为连续值，例如二值属性身高的取值，“高”“矮”可和转化为｛1.0 ， 0｝。若属性值之间不存在序的关系，例如属性“瓜类”的取值为西瓜，南瓜，冬瓜，则可转化为（0，0，1），（0，1，0），（1，0，0）。

关键词：最小二乘法（least square method）。
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。

关键词：正则化（regularization）项。
假设解一个线性方程组，当方程数大于自由变量数时，是没有解的。反过来，当方程数小于自由变量数的时候，解就有很多个了。往往，我们会碰到这种情况，参数多，“方程”少的情况，那么有很多个w（权值向量）都能使均方误差最小，那么该选哪一个呢？这就涉及到归纳偏好问题了，常见的做法是引入正则化项。

关键词：对数线性回归（log-linear regression）；y的衍生物
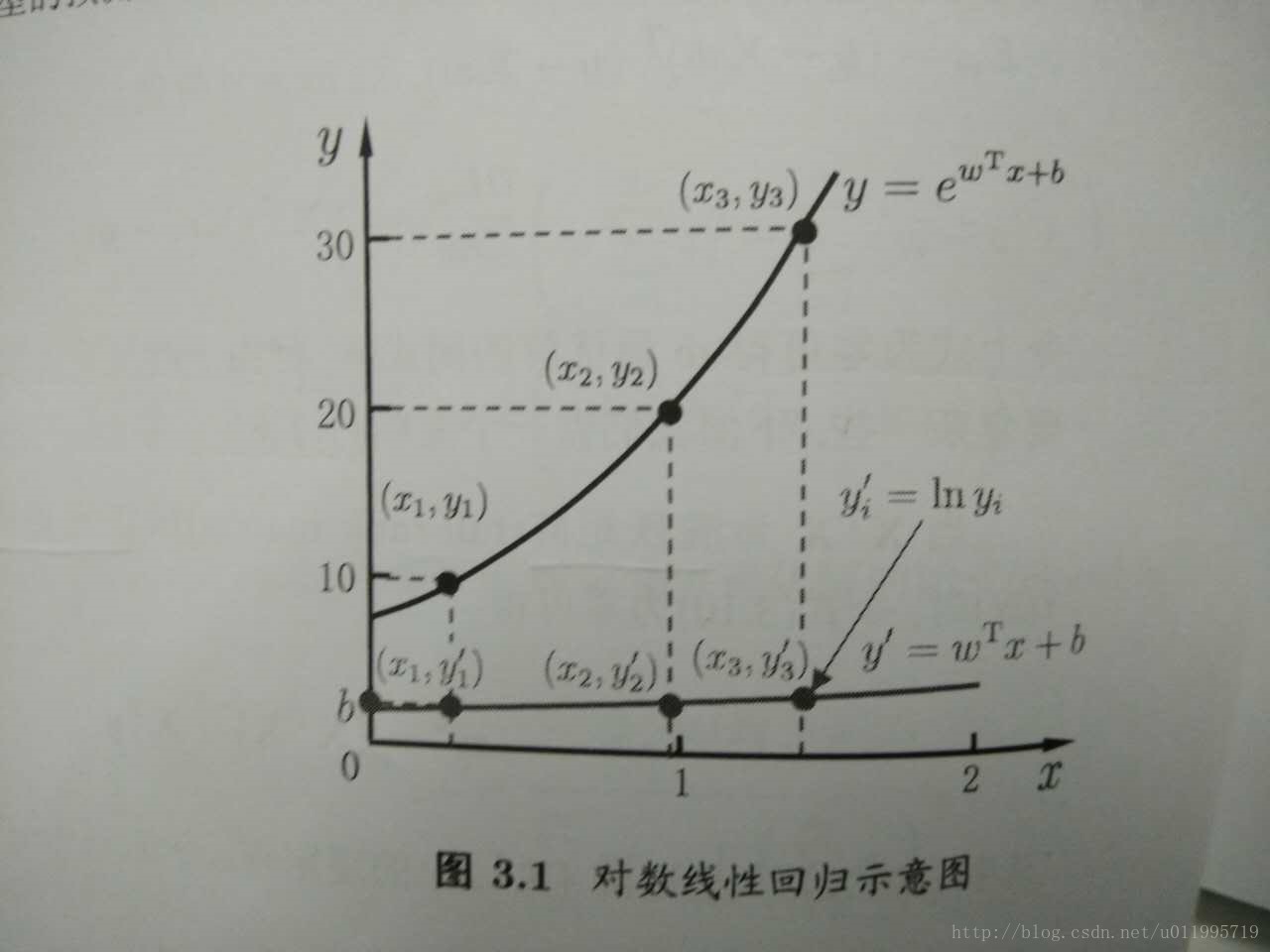
把线性回归模型简写为： $f(x)=w^{T}x+b$ ，当我们希望线性模型的预测值逼近真实标记y，这样就是线性模型。那可否令模型的预测值毕竟y的衍生物呢？作者的这一描述实在太妙了！y的衍生物，通俗易懂！假设y的衍生物是 y的对数即lny，那么就可以得到对数线性回归模型： $lny=w^{T}x+b$ ，也就是让模型去逼近 lny，而不是y。也可以对 $lny=w^{T}x+b$ 做一下变换就变成了 $y=e^{w^{T}x+b}$ ，也可以理解为让 $e^{w^{T}x+b}$ 去逼近y。形式上还是线性回归的，但实质上已是在求取输入空间到输出空间的非线性函数映射。如图：
这里写图片描述