查找算法总结

一、顺序查找和折半查找

1、顺序查找

基本思想：从线性表的一端开始，逐个检查关键字是否满足条件。找到满足条件的元素，则查找成功；若查找到线性表另一端仍没有满足条件的元素，则查找失败

int SeqSearch(int[] nums, int key){
	for(int i=0; i<nums.length; i++)
		if(key == nums[i])
			return i;
	return -1;
}

ASL(成功)=（n+1）/2；ASL(失败)=（n+1）

顺序查找缺点：当n较大时，平均查找长度较大，效率较低；

顺序查找优点：对数据元素存储没有要求，顺序存储或链式存储皆可

2、折半查找（又名二分查找）

基本思想：首先将给定值key与表中间位置元素的关键字比较，相等则查找成功并返回元素的存储位置；若不等则根据元素位置关系在表前半部分或后半部分进一步查找，不断重得至找到或确定表中没有对应元素停止

int BinarySearch(int[] nums, int key){
	int low = 0, high = nums.length-1, mid;
	while(low <= high){
		mid = (low + high) / 2;
		if(key == nums[mid])
			return mid;
		else if(key > nums[mid])
			low = mid+1;
		else high = mid-1;
	}
	return -1;
}

由上可知折半查找的比较次数最多不会超过树的高度

折半查找的缺点：适合查找的存储结构必须具有随机存取的特性，仅适合于线性表的顺序存储结构，不适合链式存储结构，且要求元素按关键字的顺序排列

3、分块查找（索引顺序查找）

基本思想：将查找表分在若干子块.块内的元素可以无序，但块之间是有序的，即第一块中的最大关键字小于第于块中所有记录的关键字，第二块中的最大关键字小于第三块中所有记录的关键字，依次类推。再建立一个索引表，索引表中的每个元素含有各块的最大关键字和各块第一个元素的地址，索引表按关键字有序排列

查找过程分两步：1）在索引表中确定待查记录所在块，可顺序查找或折半查找；2）块内执行顺序查找

二、B树及B+树

1、B树（又称多路平衡查找树）

B树中所有结点的孩子结点数的最大值称为B树的阶，通常用m表示。一棵m阶B树或为空树，或为满足如下特性的m叉树：

1）树中每个结点至多有m棵子树（即至多含有m-1个关键字）；

2）若根结点不是终端结点，则至少有两棵子树；

3）除根结点外的所有非叶子结点至少有[m/2]棵子树（至少含[m/2]-1个关键字）；

4）所有非叶结点的结构如下：

n

P0

K1

P1

K2

P2

...

Kn

Pn

其中Ki为结点的关键字，且满足K1<K2<...<Kn；Pi为指向子树根结点的指针，且指针P(i-1)所指子树中所有结点的关键字均小于Ki，Pi所指子树中所有结点的关键字均大于Ki；

5)所有的叶结点都出现在同一层次上并且不带信息

对B树的查找包含两个基本操作：1）在B树中找结点；2）在结点内找关键字

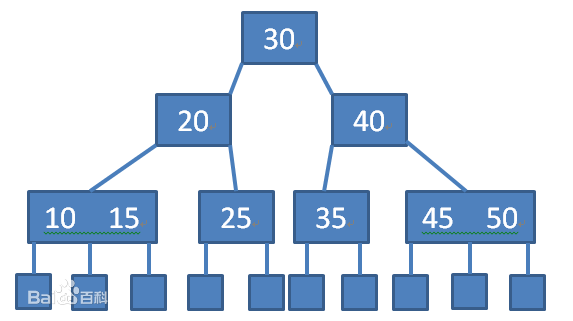
2、B+树

B+树是应数据库所需而出现的一种B树的变形树。一棵m阶的B+树满足以下条件：

1）每个分支结点最多有m棵子树（子结点）；

2）非叶根结点至少有两棵子树，其他每个分支结点至少有[m/2]棵子树；

3）结点的子树个数与关键字个数相等；

4）所有叶结点包含全部关键字及指向相应记录的指针，而且叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序相互链接起来；

5）所有分支结点（可以看成是索引的索引）中仅包含它的各个子结点（即下一级的索引块）中关键字的最大值及指向其子结点的指针

3、m阶B树与B+树的区别

1）在B+树中，具有n个关键字的结点只含有n棵子树，即每个关键字对应一棵子树；而在B树中，具有n个关键字的结点含有（n+1）棵子树；

2）在B+树中，每个结点（非根结点）的关键字个数n的范围是[m/2]<=n<=m（根结点：1<=n<=m）；在B树中，每个结点（非根结点）关键字个数n的范围是[m/2]-1<=n<=m-1（根结点：1<=n<=m-1）；

3）在B+树中，叶结点包含信息，所有非叶结点仅起到索引作用，即非叶结点只含有对应子树的最大关键字和指向该子树的指针，不含该关键字对应记录的存储地址；

4）在B+树中，叶结点包含了全部关键字，即在非叶结点中出现的关键字也会出现在叶结点中；而在B树中，叶结点包含的关键字和其他结点包含的关键字是不重复的

通常在B+树中有两个头指针：一个指向根结点，别一个指向关键字最小的叶结点

所以可以对B+树进行两种查找运算：从最小关键字开始顺序查找；从根结点开始多路查找

三、散列表

1、开放地址查找

2、拉链法查找