机器学习的领域内涉及了大量的学习算法。算法多了,如何评价一个算法性能的优良程度,如何为特定的问题选择一个合适的算法,这都是需要解决的问题。泛化误差,交叉验证和特征选择就分别在不同的层次上解决了这个问题。
泛化误差
要评价一个预测算法的优劣,标准无非就是比较预测结果和真实结果的差别,差别越小,这个算法性能就越好,由此给出了经验风险的表达式

其中,L(Y,f(X))叫做损失函数,它是用来量化真实结果Y和预测结果f(X)的区别大小的。
如果我们对已知的样本,用经验风险最小化的标准来选择算法,我们就一定会选择经验风险最小的算法。这样,就会产生过拟合的问题。导致我们得到的算法在样本集上的测试结果非常优秀,但是在真实的预测中,却不尽如人意。换一种说法,就是这种算法的泛化能力比较差。
参考李航的统计学习方法,学习方法的泛化能力往往都是通过研究泛化误差的概率上界来进行的。也就是说,泛化误差上界量化了在最坏的情况下,一个学习算法的优略程度。
泛化误差的计算公式如下
其中不等式右边的R(f)是经验风险,N为样本数量,d为假设空间内的分类器个数。具体请参考《统计学习方法》。当假设空间推广到无限的时候,参考Andrew的说法,我的理
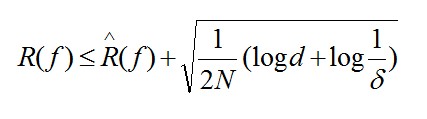 解
是:假设学习算法的评分为y(越高越好),经验风险为b,假设空间的VC维是x,样本数量为a,那么不严格地说,它们之间服从y=x/a+b这个线性的关系(存在特例)。
解
是:假设学习算法的评分为y(越高越好),经验风险为b,假设空间的VC维是x,样本数量为a,那么不严格地说,它们之间服从y=x/a+b这个线性的关系(存在特例)。
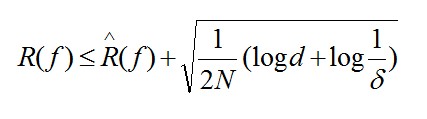 解
是:假设学习算法的评分为y(越高越好),经验风险为b,假设空间的VC维是x,样本数量为a,那么不严格地说,它们之间服从y=x/a+b这个线性的关系(存在特例)。
解
是:假设学习算法的评分为y(越高越好),经验风险为b,假设空间的VC维是x,样本数量为a,那么不严格地说,它们之间服从y=x/a+b这个线性的关系(存在特例)。
交叉验证
泛化误差从宏观上给出了算法的优劣评分,但是这个评分收敛于算法的误差上界。而在实际应用中,误差上界往往非常大,不具有实际的参考价值。因此,评价一个学习算法是否适合于某一实际的问题,就要用交叉验证的方法来实际测试。
为了避免过拟合的问题,交叉验证把训练数据分成了训练集和测试集,用训练集来训练学习算法,再用测试集来验证学习算法,每次都从候选的学习算法集合中选择一个算法,进行学习和测试,最后比较所有算法的测试结果,选择最优的算法。
参考JerryLead的笔记,简单交叉验证的算法如下:

但是简单交叉验证还是不能充分得利用所有数据。在数据特别珍贵的情况下,对造成了数据资源的浪费。因此,某些情况下,会再次改进这个算法,采用K-折叠交叉验证,算法如下:

在极端情况下,K等于训练集数据的数量S,要进行K次的训练和测试,这种情况下的交叉验证被称为留一交叉验证。
假设样本的维度n非差大,而每一个维度都代表了一个表征这个数据的特征。当数据的特征非常多时,我们就需要通过某种方式来过滤掉一些冗余的特征,提高数据的质量,这就是特征选择的目的。
第一种方法叫做前向搜索,它的主要特点是每次从特征集中选出一个测试效果最好的特征,直到满足相应条件为止,具体算法如下:

这种算法的计算复杂度较大,为O(n2)
第二种方法叫做过滤特征选择,它的主要特点是分别计算每一个特征相对于类别标签y的信息量,最后把信息量的值从大到小排列,选取最优的K个值所代表的特征。信息量的计算公式参考KL距离的计算方法得到,公式如下:
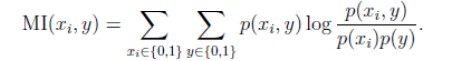
这种算法的计算复杂度较之前者较小,为O(n)。






















 1100
1100

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








