【Kaggle】电信用户流失预测分析

最新推荐文章于 2025-03-02 16:17:15 发布

向云端UP

最新推荐文章于 2025-03-02 16:17:15 发布

阅读量1k

点赞数 27

分类专栏：机器学习模型文章标签： python

本文链接：https://blog.csdn.net/u012121721/article/details/145115265

版权

机器学习模型专栏收录该内容

21 篇文章

订阅专栏

一、业务背景及目标

在电信行业，如何基于用户信息和行为精准营销，以满足用户多样化、个性化需求，是运营商面临的关键课题。公共客户（个人或家庭用户）具备易变性和替代性，需求弹性小且购买周期长，这使得新用户获取成本高昂，维系现有客户、防止流失成为核心运营策略。尽管用户流失可能受到偶然因素影响，但通过对用户属性和行为数据的深度分析，可以挖掘潜在流失因素。若能实时接入数据并结合预测模型，不仅能提前预判用户流失风险，还能制定有效挽留策略，降低用户流失率，提升运营效率。
综上所述，建模目标有两个，其一是对流失用户进行预测，其二则是找出影响用户流失的重要因子，来辅助运营人员来进行营销策略调整或制定用户挽留措施。

二、构建模型

2.1、数据集介绍

本次案例使用的数据源自Kaggle平台提供的经典建模数据集：Telco Customer Churn，该数据集全面记录了一家电信公司客户的基本信息，涵盖用户已注册的服务类型、账户详细信息、人口统计学特征、用户流失情况等多维度数据，是Kaggle平台上非常经典的围绕偏态数据集建模的数据集。
通过网盘分享的文件：WA_Fn-UseC_-Telco-Customer-Churn.csv
链接: https://pan.baidu.com/s/1E_QOEUHzH61_g9K3fG-xnQ 提取码: 6kfh

2.2、数据探索性分析

import numpy as np
import pandas as pd
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
tcc.info()

在这里插入图片描述
数据集中各字段解释如下：

字段	解释
customerID	用户ID
gender	性别
SeniorCitizen	是否是老年人（1代表是）
Partner	是否有配偶（Yes or No）
Dependents	是否经济独立（Yes or No）
tenure	用户入网时间
PhoneService	是否开通电话业务（Yes or No）
MultipleLines	是否开通多条电话业务（Yes 、 No or No phoneservice）
InternetService	是否开通互联网服务（No、DSL数字网络或filber potic光线网络）
OnlineSecurity	是否开通网络安全服务（Yes、No or No internetservice）
OnlineBackup	是否开通在线备份服务（Yes、No or No internetservice）
DeviceProtection	是否开通设备保护服务（Yes、No or No internetservice）
TechSupport	是否开通技术支持业务（Yes、No or No internetservice）
StreamingTV	是否开通网络电视（Yes、No or No internetservice）
StreamingMovies	是否开通网络电影（Yes、No or No internetservice）
Contract	合同签订方式（按月、按年或者两年）
PaperlessBilling	是否开通电子账单（Yes or No）
PaymentMethod	付款方式（bank transfer、credit card、electronic check、mailed check）
MonthlyCharges	月度费用
TotalCharges	总费用
Churn	是否流失（Yes or No）

上述字段基本可以分为三类，分别是用户人口统计信息、用户已注册的服务信息 和 用户账户信息 ，三类字段划分情况如下：
在这里插入图片描述

2.2.1 数据集正确性校验

数据集正确性校验分为两种，其一是检验数据集字段是否和数据字典中的字段一致，其二则是检验数据集中ID列有无重复。

tcc['customerID'].nunique() == tcc.shape[0]  #输出 True 即ID列没有重复
tcc.duplicated().sum() #0 即数据集中也不存在完全重复的两行数据

2.2.2 数据集缺失值检查

通过isnull来快速查看数据集缺失情况。

tcc.isnull().sum()

在这里插入图片描述
通过定义函数来输出更加完整的每一列缺失值的数值和占比：

def missing (df):
    """
    计算每一列的缺失值及占比
    """
    missing_number = df.isnull().sum().sort_values(ascending=False)      # 每一列的缺失值求和后降序排序                  
    missing_percent = (df.isnull().sum()/df.isnull().count()).sort_values(ascending=False) # 每一列缺失值占比
    missing_values = pd.concat([missing_number, missing_percent], axis=1, keys=['Missing_Number', 'Missing_Percent'])      # 合并为一个DataFrame
    return missing_values
missing(tcc)

在这里插入图片描述

2.2.3 时序字段处理

根据数据集的 info 输出可知，大部分字段为离散型字段，且以 object 类型为主。在建模分析中，object 类型字段无法直接使用，需进行类型转换。通常情况下，我们会将字段划分为 连续型字段 和 离散型字段，并根据离散字段的具体含义进一步区分为 名义型变量 或 有序变量。
值得注意的是，在划分字段类型之前，我们发现数据集中存在一个 入网时间字段，其特征类似于时序字段。从严格意义上讲，时序字段使用时间标注，既不属于连续型字段，也不完全是离散型字段（尽管可将其视作离散型字段，但可能导致信息损失）。因此，需要重点核实该字段是否为时间标注，并进一步明确其处理方式。

tcc['tenure']

在这里插入图片描述

tcc['tenure'].nunique() #输出 73

字段并不是典型的用年月日标注的时间字段，如2025-01-13，而是73个不同的取值连续的数值。结合此前所说，数据集是第三季度的用户数据，因此推断该字段应该是经过字典排序后的离散型字段。也就是说，在第三季度中，这些用户的行为发生在某73天内，因此入网时间字段有73个取值。

2.2.4 连续/离散型变量标注

通过不同列表来存储不同类型字段的名称：

# 离散字段
category_cols = ['customerID', 'gender', 'SeniorCitizen', 'Partner', 'Dependents', 'tenure', 
                'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 
                'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 
             	'PaperlessBilling','PaymentMethod']

# 连续字段
numeric_cols = ['MonthlyCharges', 'TotalCharges']

# 标签
target = 'Churn'

# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 1 == tcc.shape[1]

大多数时候离散型字段都在读取时都是object类型，因此我们也可以通过如下方式直接提取object字段：

tcc.select_dtypes('object').columns

在这里插入图片描述
查看每个离散变量的不同取值:

tcc[category_cols].nunique()

在这里插入图片描述

for feature in tcc[category_cols]:
        print(f'{feature}: {tcc[feature].unique()}')

在这里插入图片描述

2.3、数据预处理

2.3.1 缺失值检验与填补

连续特征中存在空格，需要进一步检查空格字符出现在哪一列的哪个位置。

def find_index(data_col, val):
    """
    查询某值在某列中第一次出现位置的索引，没有则返回-1
    
    :data_col: 查询的列
    :val: 具体取值
    """
    val_list = [val]
    if data_col.isin(val_list).sum() == 0:
        index = -1
    else:
        index = data_col.isin(val_list).idxmax()
    return index
    
for col in numeric_cols:
    print(col,find_index(tcc[col], ' '))
#输出MonthlyCharges -1
#   TotalCharges 488 即空格第一次出现在'TotalCharges'列的索引值为488的位置

使用np.nan对空格进行替换，并将’MonthlyCharges’转化为浮点数类型：

tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)

再次查看连续变量的缺失值占比情况：

missing(tcc[numeric_cols])

在这里插入图片描述
由于缺失值占比较小，因此可以直接使用均值进行填充：

tcc['TotalCharges'].fillna(tcc['TotalCharges'].mean())

tcc[tcc['TotalCharges'].isnull()]

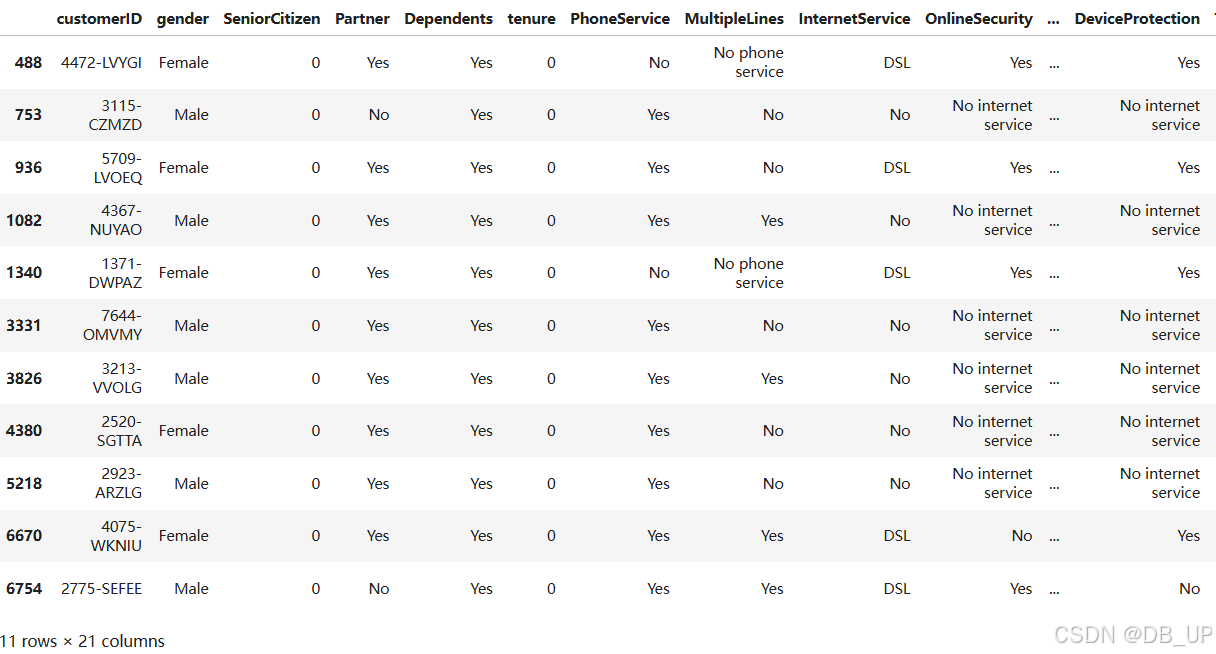
在这里插入图片描述
这11条数据的入网时间都是0，也就是说，这11位用户极有可能是在统计周期结束前的最后时间入网的用户，因此没有过去的总消费记录，但是却有当月的消费记录。也就是说，该数据集的过去总消费记录不包括当月消费记录，也就是不存在过去总消费记录等于0的记录。

(tcc['TotalCharges'] == 0).sum() #输出0

将这11条记录的缺失值记录为0，以表示在最后一个月统计消费金额前，这些用户的过去总消费金额为0:

tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)

另一种便捷的方式，即直接使用pd.to_numeric对连续变量进行转化，并在errors参数位上输入’coerce’参数，表示能直接转化为数值类型时直接转化，无法转化的用缺失值填补。

df1.TotalCharges = pd.to_numeric(df1.TotalCharges, errors='coerce')
df1.TotalCharges.isnull().sum() # 查看缺失值情况  输出 11

2.3.2 异常值检测

2.3.2.1 三倍标准差法

异常值检测有很多方法，最简单的可以通过三倍标准差法来进行检验，即以均值-3倍标注差为下界，均值+3倍标准差为上界，来检测是否有超过边界的点。也可以参考之前的异常值检测方法：异常值检测

tcc[numeric_cols].describe()
[tcc['MonthlyCharges'].mean() - 3 * tcc['MonthlyCharges'].std(),tcc['MonthlyCharges'].mean() + 3 * tcc['MonthlyCharges'].std()] #[np.float64(-25.5084488324363), np.float64(155.03183375363466)]
[tcc['TotalCharges'].mean() - 3 * tcc['TotalCharges'].std(),tcc['TotalCharges'].mean() + 3 * tcc['TotalCharges'].std()]  #[np.float64(-4517.013644807569), np.float64(9083.6145264913)]

在这里插入图片描述
数据集并不存在异常值点。

2.3.2.2 箱线图

箱线图主要借助中位数和四分位数来进行计算，以上四分位数+1.5倍四分位距为上界、下四分位数-1.5倍四分位距为下界，超出界限则认为是异常值。

import seaborn as sns
import matplotlib.pyplot as plt
Q3 = tcc[numeric_cols].describe()['MonthlyCharges']['75%'] # MonthlyCharges上四分位数
Q1 = tcc[numeric_cols].describe()['MonthlyCharges']['25%'] # MonthlyCharges下四分位数
IQR = Q3 - Q1 # MonthlyCharges的四分位距
(Q1 - 1.5 * IQR,Q3 + 1.5 * IQR) # 异常值下上界  (-46.02,171.375) 
tcc['MonthlyCharges'].min(), tcc['MonthlyCharges'].max()  #指标最小、大值(18.25, 118.75)

Q3 = tcc[numeric_cols].describe()['TotalCharges']['75%']
Q1 = tcc[numeric_cols].describe()['TotalCharges']['25%']
IQR = Q3 - Q1
(Q1 - 1.5 * IQR, Q3 + 1.5 * IQR)  #异常值下上界(-4683.525, 8868.675)
tcc['TotalCharges'].min(), tcc['TotalCharges'].max() #指标最小、大值(0.0, 8684.8)

plt.figure(figsize=(16, 6), dpi=200)
plt.subplot(121)
plt.boxplot(tcc['MonthlyCharges'])
plt.xlabel('MonthlyCharges')
plt.subplot(122)
plt.boxplot(tcc['TotalCharges'])
plt.xlabel('TotalCharges')

在这里插入图片描述
能够发现，根据箱线图的判别结果，数据并没有异常值出现。

2.3.2.3 连续变量的分布情况

通过连续变量的分布情况来观察是否存在异常值。

plt.figure(figsize=(16, 6), dpi=200)
plt.subplot(121)
sns.histplot(tcc['MonthlyCharges'], kde=True) 
plt.subplot(122)
sns.histplot(tcc['TotalCharges'], kde=True)

在这里插入图片描述
通过上述图像能基本看出月消费金额和总消费金额的基本分布情况，对于大多数用户来说月消费金额和总消费金额都较小，而月消费金额所出现的波动，极有可能是某些套餐的组合定价。

2.3.3 标签取值分析

y = tcc['Churn']
print(f'Percentage of Churn:  {round(y.value_counts(normalize=True)[1]*100,2)} %  --> ({y.value_counts()[1]} customer)\nPercentage of customer did not churn: {round(y.value_counts(normalize=True)[0]*100,2)}  %  --> ({y.value_counts()[0]} customer)')

Percentage of Churn: 26.54 % --> (1869 customer)
Percentage of customer did not churn: 73.46 % --> (5174 customer)
7000余条数据中，流失用户占比约为26%，整体来看标签取值并不均匀，但如果放到用户流失这一实际业务背景中来探讨，流失用户比例占比26%已经是非常高。

sns.displot(y)

在这里插入图片描述

2.3.4 变量相关性分析

对变量和标签进行相关性分析。从严格的统计学意义讲，不同类型变量的相关性需要采用不同的分析方法，例如连续变量之间相关性可以使用皮尔逊相关系数进行计算，而连续变量和离散变量之间相关性则可以卡方检验进行分析，而离散变量之间则可以从信息增益角度入手进行分析。但是，如果我们只是想初步探查变量之间是否存在相关关系，则可以忽略变量连续/离散特性，统一使用相关系数进行计算，这也是pandas中的.corr方法所采用的策略。

# 剔除ID列
df3 = tcc.iloc[:,1:].copy()

# 将标签Yes/No转化为1/0
df3['Churn'] = df3['Churn'].map({'Yes': 1, 'No': 0})

# 将其他所有分类变量转化为哑变量，连续变量保留不变
df_dummies = pd.get_dummies(df3)
df_dummies.head()
df_dummies.corr()  #采用.corr方法计算相关系数矩阵
df_dummies.corr()['Churn'].sort_values(ascending = False)  #特征和标签之间的相关关系

在这里插入图片描述
根据相关系数计算的基本原理，相关系数为正数，则二者为正相关，数值变化会更倾向于保持同步。例如Churn(是否流失)与Contract_Month-to-month(按月合同签订方式)相关系数为0.4，则说明二者存在一定的正相关性，即Contract_Month-to-month取值为1（更大）越有可能使得Churn取值为1。也就是在Contract字段的Month-to-month取值结果和最终流失的结果相关性较大，也就是相比其他条件，Contract取值为Month-to-month的用户流失概率较大，而tenure(用户入网时间)和Churn负相关，则说明tenure取值越大、用户流失概率越小。其他结果解读依此类推。

热力图展示相关性

plt.figure(figsize=(15,8), dpi=200)
sns.heatmap (df_dummies.corr())

在这里插入图片描述

柱状图展示相关性

sns.set()
plt.figure(figsize=(15,8), dpi=200)
df_dummies.corr()['Churn'].sort_values(ascending = False).plot(kind='bar')

在这里插入图片描述
直接计算整体相关系数矩阵并进行可视化是一种高效便捷的方式，尤其在算法竞赛中，常被用来快速完成数据相关性检验和探索。然而，对于业务分析人员来说，这种方式可能不够直观，无法清晰传达具体的相关性信息。一种有效的方式是围绕不同属性类型，利用柱状图进行可视化分析。特别是当需要对比字段不同取值下流失用户的占比时，堆叠柱状图是一种理想的选择。这种可视化形式不仅能直观展现不同字段的分布，还能清晰体现流失用户的占比差异，为业务人员提供更有价值的洞察。

用户人口统计信息(性别、是否是老人、是否有配偶、是否经济独立)

col_1 = ["gender", "SeniorCitizen", "Partner", "Dependents"]
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(16,12), dpi=200)
for i, item in enumerate(col_1):
    plt.subplot(2,2,(i+1))
    ax=sns.countplot(x=item,hue="Churn",data=tcc,palette="Blues", dodge=False)
    plt.xlabel(item)
    plt.title("Churn by "+ item)

在这里插入图片描述
老年用户、未结婚用户以及经济未独立用户流失比例相对较高，而性别因素对是否流失影响不大。在实际制定运营策略时，这三类用户需要重点关注。

已注册的服务信息（选取是否开通网络安全服务、在线备份服务、设备保护服务、技术支持业务、网络电视、网络电影）分析服务属性字段与用户流失之间的关系

col_2 = ["OnlineSecurity", "OnlineBackup", "DeviceProtection", "TechSupport", "StreamingTV", "StreamingMovies"]
fig,axes=plt.subplots(nrows=2,ncols=3,figsize=(16,12))
for i, item in enumerate(col_2):
    plt.subplot(2,3,(i+1))
    ax=sns.countplot(x=item,hue="Churn",data=tcc,palette="Blues",order=["Yes","No","No internet service"], dodge=False)
    plt.xlabel(item)
    plt.title("Churn by "+ item)

在这里插入图片描述
从整体来看，提供了附加服务的客户（如OnlineSecurity、OnlineBackup、DeviceProtection、TechSupport、StreamingTV和StreamingMovies）流失率较低。特别是DeviceProtection和OnlineSecurity的使用显著减少了客户的流失。相反，没有使用任何服务的客户流失率较高。

用户合同属性（合同签订方式、是否开通电子账单、付款方式）：分析用户合同属性与流失率之间的关系

col_3 = ["Contract", "PaperlessBilling", "PaymentMethod"]
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(16,12))
for i, item in enumerate(col_3):
    plt.subplot(2,2,(i+1))
    ax=sns.countplot(x=item,hue="Churn",data=tcc,palette="Blues", dodge=False)
    plt.xlabel(item)
    plt.title("Churn by "+ item)

在这里插入图片描述
服务周期较短的用户具有较高的流失风险，而偏好在线支付方式的客户群体似乎更易出现流失现象。

2.4 数据编码

2.4.1 离散特征编码

2.4.1.1 OrdinalEncoder自然数排序

该方法的过程较为简单，即先对离散字段的不同取值进行排序，然后对其进行自然数值取值转化。
在这里插入图片描述
对于自然数排序过程，可以通过简单的pandas中的列取值调整来进行，例如就像此前对标签字段取值的调整过程，此外也可以直接考虑调用sklearn中的OrdinalEncoder()评估器（转化器）。

from sklearn import preprocessing
X1 = np.array([['F'], ['M'], ['M'], ['F']])
# 实例化转化器
enc = preprocessing.OrdinalEncoder()
# 在X1上训练
enc.fit(X1)
# 对X1数据集进行转化
enc.transform(X1)
enc.categories_ #由于自然数是从0开始排序，因此上述映射关系为F转化为0、M转化为1。

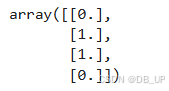
在这里插入图片描述

2.4.1.2 OneHotEncoder独热编码

除了自然顺序编码外，常见的对离散变量的编码方式还有独热编码，可以通过pd.get_dummies函数实现，也可以通过sklearn中OneHotEncoder评估器（转化器）来实现。独热编码的过程如下：
在这里插入图片描述

enc = preprocessing.OneHotEncoder()
enc.fit_transform(X1).toarray()

在这里插入图片描述
对于独热编码的使用，有一点是额外需要注意的，那就是对于二分类离散变量来说，独热编码往往是没有实际作用的。例如对于上述极简数据集而言，Gender的取值是能是M或者F，独热编码转化后，某行Gender_F取值为1、则Gender_M取值必然为0，反之亦然。因此很多时候我们在进行独热编码转化的时候会考虑只对多分类离散变量进行转化，而保留二分类离散变量的原始取值。此时就需要将OneHotEncoder中drop参数调整为’if_binary’，以表示跳过二分类离散变量列。——该过程就相当于是二分类变量进行自然数编码，对多分类变量进行独热编码。
在这里插入图片描述
对于sklearn的独热编码转化器来说，尽管其使用过程会更加方便，但却无法自动创建转化后的列名称，而在需要考察字段业务背景含义的场景中，必然需要知道每一列的实际名称（就类似于极简示例中每一列的名字，通过“原列名_字段取值”来进行命名），因此我们需要定义一个函数来批量创建独热编码后新数据集各字段名称的函数。

X3 = pd.DataFrame({'Gender': ['F', 'M', 'M', 'F'], 'Income': ['High', 'Medium', 'High', 'Low']})
# 提取原始列名称
cate_cols = X3.columns.tolist()
drop_enc = preprocessing.OneHotEncoder(drop='if_binary')
drop_enc.fit_transform(X3).toarray()
# 新编码字段名称存储
cate_cols_new = []
# 提取独热编码后所有特征的名称
for i, j in enumerate(cate_cols):
    if len(drop_enc.categories_[i]) == 2:
        cate_cols_new.append(j)
    else:
        for f in drop_enc.categories_[i]:
            feature_name = j + '_' + f
            cate_cols_new.append(feature_name)
cate_cols_new # 查看新字段名称提取结果

输出：[‘Gender’, ‘Income_High’, ‘Income_Low’, ‘Income_Medium’]
在这里插入图片描述

# 组合成新的DataFrame
pd.DataFrame(drop_enc.fit_transform(X3).toarray(), columns=cate_cols_new)

在这里插入图片描述

封装成函数

def cate_colName(Transformer, category_cols, drop='if_binary'):
    """
    离散字段独热编码后字段名创建函数
    :Transformer: 独热编码转化器
    :category_cols: 输入转化器的离散变量
    :drop: 独热编码转化器的drop参数
    """
    cate_cols_new = []
    col_value = Transformer.categories_
    
    for i, j in enumerate(category_cols):
        if (drop == 'if_binary') & (len(col_value[i]) == 2):
            cate_cols_new.append(j)
        else:
            for f in col_value[i]:
                feature_name = j + '_' + f
                cate_cols_new.append(feature_name)
    return(cate_cols_new)

enc = preprocessing.OneHotEncoder(drop='if_binary')
df_cate = tcc[category_cols]
enc.fit(df_cate)
pd.DataFrame(enc.transform(df_cate).toarray(), columns=cate_colName(enc, category_cols))

在这里插入图片描述

2.4.1.3 ColumnTransformer转化流水线

在执行单独的转化器时，需要单独将要转化的列提取出来，然后对其转化，并且在转化完成后再和其他列拼接成新的数据集。尽管很多时候表格的拆分和拼接不可避免，但该过程显然不够“自动化”。在sklearn的0.20版本中，加入了ColumnTransformer转化流水线评估器，该评估器和pipeline类似，能够集成多个评估器（转化器），并一次性对输入数据的不同列采用不同处理方法，并输出转化完成并且拼接完成的数据。

from sklearn.compose import ColumnTransformer
preprocess_col = ColumnTransformer([
    ('cat', preprocessing.OneHotEncoder(drop='if_binary'), category_cols), 
    ('num', 'passthrough', numeric_cols)
])
preprocess_col.fit(tcc)

在这里插入图片描述
preprocess_col表示对数据集的离散变量进行多分类独热编码处理，对连续变量不处理。

# 转化后离散变量列名称
category_cols_new = cate_colName(preprocess_col.named_transformers_['cat'], category_cols)
cols_new = category_cols_new + numeric_cols
pd.DataFrame(preprocess_col.transform(tcc), columns=cols_new) # 输出最终dataframe

在这里插入图片描述

2.4.2 连续字段的特征变换

2.4.2.1 数据标准化与归一化

sklearn中归一化是分为标准化（Standardization）和归一化（Normalization）两类，都属于Standardization的范畴；Normalization则特指针对单个样本（一行数据）利用其范数进行放缩的过程。不过二者都属于数据预处理范畴，都在sklearn中的Preprocessing模块下。具体数据标准化与归一化的细节可以参考Scikit-Learn快速入门

2.4.2.2 连续变量分箱

连续变量的离散化，也称为分箱，是将连续型数据转换为离散型数据的过程。这一过程不仅改变了字段的原始含义，还引入了新的信息层次。例如，原始字段“Income”反映的是用户的真实收入，而离散化后则转变为收入等级的划分，如0代表低收入、1代表中等收入、2代表高收入。这种转换有助于更简洁、清晰地展示特征信息，并显著降低异常值（如收入为180的用户）对模型的影响，同时消除了不同特征间的量纲差异。
对于线性模型而言，连续变量的分箱实际上是在模型中引入了非线性因素，这有助于提升模型的预测性能。然而，分箱过程不可避免地会导致部分信息的丢失，这对于某些模型（如决策树）可能会影响其最终效果。因此，分箱策略的制定需要综合考虑业务需求和 计算流程，以确保在简化数据的同时，最大限度地保留关键信息，从而优化模型的表现。
在这里插入图片描述

2.4.2.2.1 等宽分箱

所谓等宽分箱，需要先确定划分成几份，然后根据连续变量的取值范围划分对应数量的宽度相同的区间，并据此对连续变量进行分箱，在sklearn的预处理模块中调用KBinsDiscretizer转化器实现该功能。
在这里插入图片描述

# 转化为列向量
import pandas as np
income = np.array([0, 10, 180, 30, 55, 35, 25, 75, 80, 10]).reshape(-1, 1) #一列特征必须以列向量呈现，才能够被KBinsDiscretizer正确识别
# 三分等宽分箱，strategy选择'uniform'
dis = preprocessing.KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
'''n_bins参数位上输入需要分箱的个数，strategy参数位上输入等宽分箱、等频分箱还是聚类分箱，
   encode参数位上输入分箱后的离散字段是否需要进一步进行独热编码处理或者自然数编码。'''
dis.fit_transform(income)

#在分箱结束后，可以通过.bin_edges_查看分箱依据（每个箱体的边界）。
dis.bin_edges_

在这里插入图片描述

2.4.2.2.2 等频分箱

在等频分箱的过程中，需要先确定划分成几份，然后选择能够让每一份包含样本数量相同的划分方式。对于上述数据集，若需要分成两份，则需要先对所有数据进行排序，然后选取一个中间值对其进行切分，如果样本数量无法整除等频分箱的箱数，则最后一个“箱子”将包含余数样本。例如对10条样本进行三分等频分箱，则会分为3/3/4的结果，对于income来说，“中间值”应该是32.5，因此以32.5作为切分依据，对其进行分箱处理：
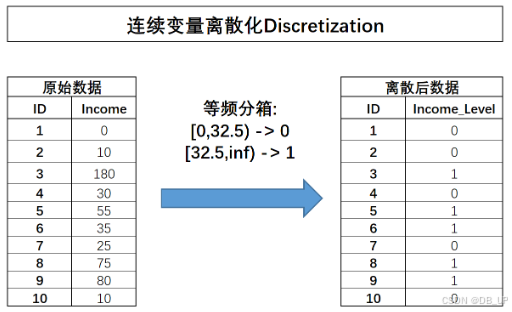
在这里插入图片描述

# np.sort(income.flatten(), axis=0)
dis = preprocessing.KBinsDiscretizer(n_bins=2, encode='ordinal', strategy='quantile')
dis.fit_transform(income),dis.bin_edges_

在这里插入图片描述
综上分析，等宽分箱会一定程度受到异常值的影响，而等频分箱又容易完全忽略异常值信息，从而一定程度上导致特征信息损失，而若要更好的兼顾变量原始数值分布，则可以考虑使用聚类分箱。

2.4.2.2.3 聚类分箱

先对某连续变量进行聚类（往往是KMeans聚类），然后用样本所属类别作为标记代替原始数值，从而完成分箱的过程。

from sklearn import cluster
kmeans = cluster.KMeans(n_clusters=3)
kmeans.fit(income)
kmeans.labels_ #通过.labels_查看每条样本所属簇的类别

在这里插入图片描述

该过程将第三条数据单独划分成了一类，这也满足了此前所说的一定程度上保留异常值信息这一要求，能够发现，聚类过程能够更加完整的保留原始数值分布信息。
KBinsDiscretizer转化器中也集成了利用KMeans进行分箱的过程，只需要在strategy参数中选择’kmeans’即可：

# 两分等频分箱，strategy选择'kmeans'
dis = preprocessing.KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans')
dis.fit_transform(income),dis.bin_edges_

在这里插入图片描述
在实际建模过程中，如无其他特殊要求，建议优先考虑聚类分箱方法。

2.4.2.2.4 有监督分箱

无论是等宽/等频分箱，还是聚类分箱，本质上都是进行无监督的分箱，即在不考虑标签的情况下进行的分箱。而在所有的分箱过程中，还有一类是有监督分箱，即根据标签取值对连续变量进行分箱。在这些方法中，最常用的分箱就是树模型分箱。
树模型的分箱有两种，其一是利用决策树模型进行分箱，简单根据决策树的树桩（每一次划分数据集的切分点）来作为连续变量的切分依据，由于决策树的分叉过程总是会选择让整体不纯度降低最快的切分点，因此这些切分点就相当于是最大程度保留了有利于样本分类的信息。

from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
import seaborn as sns
import matplotlib.pyplot as plt
income = np.array([0, 10, 180, 30, 55, 35, 25, 75, 80, 10]).reshape(-1, 1)
y = np.array([1, 1, 0, 1, 0, 0, 0, 1, 0, 0])
clf = DecisionTreeClassifier().fit(income, y)
plt.figure(figsize=(6, 2), dpi=150)
tree.plot_tree(clf)

在这里插入图片描述
需要对income进行三类分箱的话，则可以选择32.5和65作为切分点，对数据集进行切分：

2.4.3 连续变量特征转化的ColumnTransformer集成

对于连续变量的标准化或分箱操作，可以方便地集成到 ColumnTransformer 中，这种方式在处理复杂的特征工程时尤为高效。例如，当需要对离散字段进行独热编码，同时对连续字段进行标准化时，可以构建如下转换管道，实现清晰且模块化的特征预处理流程。以下是优化后的描述和代码示例：

import pandas as pd
from sklearn.compose import ColumnTransformer
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
                'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 
                'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 	 
                'PaperlessBilling','PaymentMethod']
# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']
ColumnTransformer([
    ('cat', preprocessing.OneHotEncoder(drop='if_binary'), category_cols), 
    ('num', preprocessing.StandardScaler(), numeric_cols)
])

在这里插入图片描述

ColumnTransformer([
    ('cat', preprocessing.OneHotEncoder(drop='if_binary'), category_cols), 
    ('num', preprocessing.KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans'), numeric_cols)
])

在这里插入图片描述

2.5 逻辑回归模型训练

from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.compose import ColumnTransformer #特征转换器
from sklearn.preprocessing import OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
import pandas as pd

# 加载数据
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')

# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
                'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 
                'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 'PaperlessBilling',
                'PaymentMethod']

# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']

# 标签
target = 'Churn'

# ID列
ID_col = 'customerID'

# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 2 == tcc.shape[1]
# 处理 TotalCharges 列，将空字符串替换为 NaN，并转换为数值类型
tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)

# 显式处理替换，避免 Pandas 的隐式行为
tcc['Churn'] = tcc['Churn'].map({'Yes': 1, 'No': 0})

# 数据集划分
train, test = train_test_split(tcc, test_size=0.3, random_state=21)
X_train = train.drop(columns=[ID_col, target]).copy()
y_train = train['Churn'].copy()
X_test = test.drop(columns=[ID_col,target]).copy()
y_test = test['Churn'].copy()

# 设置特征转换器
logistic_pre = ColumnTransformer([
    # 分类特征使用独热编码
    ('cat', OneHotEncoder(drop='if_binary'), category_cols),
    # 数值特征：填补缺失值后直接传递
    ('num', make_pipeline(SimpleImputer(strategy='mean'), 'passthrough'), numeric_cols)
])

# 实例化逻辑回归模型
logistic_model = LogisticRegression(max_iter=int(1e5))  # 转换为整数

# 构建流水线
logistic_pipe = make_pipeline(logistic_pre, logistic_model)

# 模型训练
logistic_pipe.fit(X_train, y_train)

# 输出训练集和测试集准确率
train_score = logistic_pipe.score(X_train, y_train)
test_score = logistic_pipe.score(X_test, y_test)

print(f"Training Accuracy: {train_score:.4f}")
print(f"Testing Accuracy: {test_score:.4f}")

在这里插入图片描述

from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score, roc_auc_score
def result_df(model, X_train, y_train, X_test, y_test, metrics=
              [accuracy_score, recall_score, precision_score, f1_score, roc_auc_score]):
    res_train = []
    res_test = []
    col_name = []
    for fun in metrics:
        res_train.append(fun(model.predict(X_train), y_train))
        res_test.append(fun(model.predict(X_test), y_test)) 
        col_name.append(fun.__name__)
    idx_name = ['train_eval', 'test_eval']
    res = pd.DataFrame([res_train, res_test], columns=col_name, index=idx_name)
    return res
result_df(logistic_pipe, X_train, y_train, X_test, y_test)

在这里插入图片描述

超参数调优

逻辑回归评估器的所有参数解释如下：

参数	解释
penalty	正则化项
dual	是否求解对偶问题*
tol	迭代停止条件：两轮迭代损失值差值小于tol时，停止迭代
C	经验风险和结构风险在损失函数中的权重
fit_intercept	线性方程中是否包含截距项
intercept_scaling	相当于此前讨论的特征最后一列全为1的列，当使用liblinear求解参数时用于捕获截距
class_weight	各类样本权重*
random_state	随机数种子
solver	损失函数求解方法*
max_iter	求解参数时最大迭代次数，迭代过程满足max_iter或tol其一即停止迭代
multi_class	多分类问题时求解方法*
verbose	是否输出任务进程
warm_start	是否使用上次训练结果作为本次运行初始参数
l1_ratio	当采用弹性网正则化时， $l 1$ 正则项权重，就是损失函数中的 $\rho$

所有超参数中，对模型结果影响较大的参数主要有两类，其一是正则化项的选择，同时也包括经验风险项的系数与损失求解方法选择，第二类则是迭代限制条件，主要是max_iter和tol两个参数。

from sklearn.model_selection import GridSearchCV
logistic_param = [
    {'logisticregression__penalty': ['l1'], 'logisticregression__C': np.arange(0.1, 2.1, 0.1).tolist(), 'logisticregression__solver': ['saga']}, 
    {'logisticregression__penalty': ['l2'], 'logisticregression__C': np.arange(0.1, 2.1, 0.1).tolist(), 'logisticregression__solver': ['lbfgs', 'newton-cg', 'sag', 'saga']}, 
    {'logisticregression__penalty': ['elasticnet'], 'logisticregression__C': np.arange(0.1, 2.1, 0.1).tolist(), 'logisticregression__l1_ratio': np.arange(0.1, 1.1, 0.1).tolist(), 'logisticregression__solver': ['saga']}
]
''''elasticnet': 混合正则化（L1和L2的加权组合）。优化算法的选择，具体包括：'saga': 支持L1、L2和ElasticNet正则化，适用于大数据。'lbfgs': 二阶优化算法，适用于L2正则化。
'newton-cg': 二阶优化算法，适用于L2正则化。'sag': 梯度下降方法，适用于L2正则化。'''
# 实例化网格搜索评估器
logistic_search = GridSearchCV(estimator = logistic_pipe,
                               param_grid = logistic_param,
                               n_jobs = 12)
import time
# 在训练集上进行训练
s = time.time()
logistic_search.fit(X_train, y_train)
print(time.time()-s, "s")
logistic_search.best_score_,logistic_search.best_params_

在这里插入图片描述

# 计算预测结果
result_df(logistic_search.best_estimator_, X_train, y_train, X_test, y_test)

在这里插入图片描述
.best_score_返回的是在网格搜索的交叉验证过程中（默认是五折验证）验证集上准确率的平均值

2.6 决策树模型

# 导入决策树评估器
from sklearn.tree import DecisionTreeClassifier
# 加载数据
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
                'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 
                'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract',  
                'PaperlessBilling', 'PaymentMethod']

# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']

# 标签
target = 'Churn'

# ID列
ID_col = 'customerID'

tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)

# 设置转化器流
tree_pre = ColumnTransformer([
    ('cat', preprocessing.OrdinalEncoder(), category_cols), 
    ('num', 'passthrough', numeric_cols)
])

# 实例化决策树评估器
tree_model = DecisionTreeClassifier()

# 设置机器学习流
tree_pipe = make_pipeline(tree_pre, tree_model)
# 模型训练
tree_pipe.fit(X_train, y_train)
# 计算预测结果
result_df(tree_pipe, X_train, y_train, X_test, y_test)

在这里插入图片描述
模型严重过拟合，即在训练集上表现较好，但在测试集上表现一般。此时可以考虑进行网格搜索，通过交叉验证来降低模型结构风险。

2.6.1 决策树优化

决策树模型的参数解释如下：

Name	Description
criterion	规则评估指标或损失函数，默认基尼系数，可选信息熵
splitter	树模型生长方式，默认以损失函数取值减少最快方式生长，可选随机根据某条件进行划分
max_depth	树的最大生长深度，类似max_iter，即总共迭代几次
min_samples_split	内部节点再划分所需最小样本数
min_samples_leaf	叶节点包含最少样本数
min_weight_fraction_leaf	叶节点所需最小权重和
max_features	在进行切分时候最多带入多少个特征进行划分规则挑选
random_state	随机数种子
max_leaf_nodes	叶节点最大个数
min_impurity_decrease	数据集再划分至少需要降低的损失值
min_impurity_split	数据集再划分所需最低不纯度，将在0.25版本中移除
class_weight	各类样本权重
presort	已在0.24版本中移除
ccp_alpha	在执行CART树原生原理中的剪枝流程时结构复杂度惩罚因子的系数，默认情况下不使用该方法进行剪枝

# 构造包含阈值的参数空间
tree_param = {'decisiontreeclassifier__ccp_alpha': np.arange(0, 1, 0.1).tolist(),
              'decisiontreeclassifier__max_depth': np.arange(2, 8, 1).tolist(), 
              'decisiontreeclassifier__min_samples_split': np.arange(2, 5, 1).tolist(), 
              'decisiontreeclassifier__min_samples_leaf': np.arange(1, 4, 1).tolist(), 
              'decisiontreeclassifier__max_leaf_nodes':np.arange(6,10, 1).tolist()}
# 实例化网格搜索评估器
tree_search = GridSearchCV(estimator = tree_pipe,
                           param_grid = tree_param,
                           n_jobs = 12)
# 在训练集上进行训练
s = time.time()
tree_search.fit(X_train, y_train)
print(time.time()-s, "s")  #输出55.11898183822632 s
# 查看验证集准确率均值
tree_search.best_score_  #输出0.79026369168357
# 查看最优参数组
tree_search.best_params_
# 计算预测结果
result_df(tree_search.best_estimator_, X_train, y_train, X_test, y_test)

在这里插入图片描述
经过网格搜索和交叉验证后，决策树的过拟合问题已经的到解决，并且最终预测结果与逻辑回归类似。

2.6.2 决策树模型解释

特征重要性为0表示该列特征并未在树模型生长过程中提供分支依据。

fi = tree_search.best_estimator_.named_steps['decisiontreeclassifier'].feature_importances_
fi

在这里插入图片描述

以列名作为index、以特征重要性值作为数值，构建Series

col_names = category_cols + numeric_cols
feature_importances = pd.Series(fi, index=col_names)
feature_importances

在这里插入图片描述

feature_importances.sort_values(ascending = False)[:5].plot(kind='bar')

在这里插入图片描述

import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
plt.figure(figsize=(16, 6), dpi=200)
tree.plot_tree(tree_search.best_estimator_.named_steps['decisiontreeclassifier'])