图像缩放双三次插值 (Bicubic) C++

生活需要深度

已于 2024-08-07 15:01:46 修改

阅读量2.7k

点赞数 15

文章标签：双线性插值算法

于 2024-07-03 17:46:48 首次发布

本文链接：https://blog.csdn.net/u012294613/article/details/140158737

版权

OpenCV 专栏收录该内容

67 篇文章

订阅专栏

1. 立方插值

立方插值算法也被称为双三次、双立方插值算法。

1.1 三次插值 (Cubic Interpolation)

先介绍一下三次插值算法，它是一种使用三次多项式拟合一组数据的插值方法。三次插值通常用于图像缩放和重采样。

三次插值的实现方式有很多种，例如牛顿多项式插值、拉格朗日多项式插值、Hermite 三次多项式插值、三次样条插值，每种方式都有其自身的优点和复杂性。

插值多项式的形式

牛顿多项式插值: 使用差商形式来构造插值多项式。
拉格朗日多项式插值: 使用乘积形式来构造插值多项式。
Hermite 三次多项式插值: 使用分段三次多项式来构造插值多项式，每个分段多项式满足插值点处的函数值和一阶导数值。
三次样条插值: 也使用分段三次多项式来表示插值多项式，将插值区间划分为多个子区间，在每个子区间上使用三次��项式插值，并要求相邻子区间插值函数在连接处的一阶导数和二阶导数连续。

适用范围

牛顿多项式插值: 适用于数据量较小、插值精度要求不高的场景，如数据拟合、数值计算等。
拉格朗日多项式插值: 适用于理论分析、教学演示等场景。
Hermite 三次多项式插值: 适用于需要高精度插值和光滑曲线的场景，如计算机图形学、曲线拟合等。
三次样条插值: 适用于数据量较大、要求插值精度和曲线光滑的场景，如图像处理、工程设计等。

1.2 三次样条插值 (Cubic Spline Interpolation)

我们以三次样条插值为例进行详细说明。

在数值分析这个数学分支中，样条插值是使用一种名为样条的特殊分段多项式进行插值的形式。由于样条插值可以使用低阶多项式样条实现较小的插值误差，这样就避免了使用高阶多项式所出现的龙格现象，所以样条插值得到了流行。

三次样条函数的定义：

函数 S(x)∈C2[a,b]S(x)\in C^2[a, b]S(x)∈C2[a,b]，且在每个小区间 [xix_ixi，xi+1x_{i+1}xi+1] 上是三次多项式，其中 a= x0x_0x0 < x1x_1x1 < . . . < xnx_nxn= b是给定节点，则称 S(x) 是节点 x0x_0x0, x1x_1x1, . . . , xnx_nxn上的三次样条函数。

三次样条函数满足：

在每个分段小区间 [xix_ixi, xi+1x_{i+1}xi+1] 上，S(x)=Si(x)S(x) = S_i(x)S(x)=Si(x)，且是一个三次方程
满足插值条件，S(xi)=yiS(x_i) = y_iS(xi)=yi(i=0,1,...,n)
S(x) 曲线是光滑的，S(x)、S'(x)、S''(x) 在[a,b] 是连续的

三次样条函数.png

要求出 S(x)，在每个小区间 [xix_ixi, xi+1x_{i+1}xi+1] 上要确定 4 个待定系数，共有 n 个区间，共 4n 个参数要构建 4n 个方程。

根据插值条件，在节点 xix_ixi(i=1,2,...n-1) 处满足：

Si(xi+1)=yi+1S_i(x_{i+1}) = y_{i+1}Si(xi+1)=yi+1

Si+1(xi+1)=yi+1S_{i+1}(x_{i+1}) = y_{i+1}Si+1(xi+1)=yi+1

以及第一个和最后一个端点分别满足三次方程，总共 2n 个方程

根据 S(x) 在 [a,b] 上一阶导和二阶导数连续，在节点 xix_ixi(i=1,2,...n-1) 处满足连续条件：

n-1 个内部点的一阶导数应该是连续的，即在第 i 区间的末点和第 i+1 区间的起点是同一个点，它们的一阶导数也相等，即：Si′(xi+1)=Si+1′(xi+1)S'_i(x_{i+1}) = S'_{i+1}(x_{i+1})Si′(xi+1)=Si+1′(xi+1)

同理：Si′′(xi+1)=Si+1′′(xi+1)S_i''(x_{i+1}) = S_{i+1}''(x_{i+1})Si′′(xi+1)=Si+1′′(xi+1)

总共 2n-2 个方程。

加起来一共 4n-2 个方程，还需再加上 2 个方程就可以确定 S(x)。通常可在区间 [a,b] 端点 a = x0x_0x0, b = xnx_nxn 处各加一个条件（称为边界条件），可根据实际问题的要求给定。常见有以下三种：

固定边界(Clamped)：已知两端的一阶导数值 A 和 B

S0′(x0)=AS_0'(x_0)=A S0′(x0)=A

Sn−1′(xn)=BS_{n-1}'(x_n)=BSn−1′(xn)=B

自然边界(Natural)：已知两端的二阶导数为 0

S′′(x0)=S′′(xn)=0S''(x_0)=S''(x_n)=0S′′(x0)=S′′(xn)=0

非扭结边界(Not-A-Knot): 强制第一个插值点的三阶导数值等于第二个点的三阶导数值，最后第一个点的三阶导数值等于倒数第二个点的三阶导数值。

S0′′′(x0)=S1′′′(x1)S_0'''(x_0)=S_1'''(x_1)S0′′′(x0)=S1′′′(x1)

Sn−2′′′(xn−1)=Sn−1′′′(xn)S_{n-2}'''(x_{n-1})=S_{n-1}'''(x_n)Sn−2′′′(xn−1)=Sn−1′′′(xn)

1.3 双三次样条插值 (Bicubic Spline Interpolation)

双三次样条插值是在二维空间中使用三次样条函数对图像进行插值。它将图像划分为一个网格，并在每个网格点处使用一个三次样条函数来拟合图像数据。在未知点处，通过对相邻网格点的三次样条函数进行插值来获得插值值。

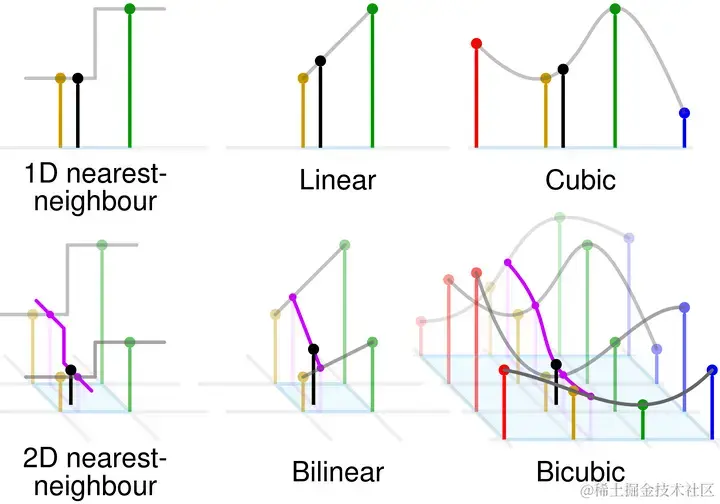
各种插值函数的对比.png

构造 Bicubic 函数：

W(x)={(a+2)∣x∣3−(a+3)∣x∣2+1for |x|≤1a∣x∣3−5a∣x∣2+8a∣x∣−4afor 1 <|x|<20otherwiseW(x) = \begin{cases} (a+2)|x|^3-(a+3)|x|^2+1 & \text{for |x|} \le 1\\ a|x|^3-5a|x|^2+8a|x|-4a & \text{for 1 <|x|<2}\\ 0 & \text{otherwise} \end{cases}W(x)=⎩⎨⎧(a+2)∣x∣3−(a+3)∣x∣2+1a∣x∣3−5a∣x∣2+8a∣x∣−4a0for |x|≤1for 1 <|x|<2otherwise

对待插值的像素点(x,y)，取其附近的 4*4 邻域点(xix_ixi,yiy_iyi) (i,j=0,1,2,3)。其插值公式如下：

f(x,y)=∑i=03∑j=03f(xi,yj)W(x−xi)W(y−yj)f(x,y)=\sum_{i=0}^{3}\sum_{j=0}^{3}f(x_i,y_j)W(x-x_i)W(y-y_j)f(x,y)=∑i=03∑j=03f(xi,yj)W(x−xi)W(y−yj)

2. Lanczos 插值 (Lanczos Interpolation)

Lanczos 插值使用 Lanczos 核函数来计算插值后的像素值。Lanczos 核函数是一种低通滤波器，可以消除缩放过程中产生的混叠现象。

Lanczos 核函数定义如下：

L(x)={sinc(x)sinc(x/a),if −a<x<a,0,otherwise.L(x) = \begin{cases} sinc(x)sinc(x/a), & \text{if } -a < x < a, \\ 0, & otherwise. \end{cases}L(x)={sinc(x)sinc(x/a),0,if −a<x<a,otherwise.

其中，sinc(x) = sin(πx) / (πx)，a 是核函数的宽度。

Lanczos 插值的过程如下：

确定插值点的位置。
以插值点为中心，在原图像中取一个窗口。
对窗口中的每个像素，使用 Lanczos 核函数计算其权重。
将窗口中所有像素的权重和插值值相乘，得到插值点的最终值。

Lanczos 插值公式：

S(x)=∑i=⌊x⌋−a+1⌊x⌋+asiL(x−i)S(x) = \sum_{i=\lfloor x \rfloor-a+1}^{\lfloor x \rfloor+a} s_iL(x-i)S(x)=∑i=⌊x⌋−a+1⌊x⌋+asiL(x−i)

Lanczos 插值的优点

与其他插值方法相比，Lanczos 插值可以产生更清晰、更平滑的图像。
Lanczos 插值可以有效地抑制混叠现象，尤其是在图像缩小的情况下。

Lanczos 插值的缺点

与其他的插值方法相比，Lanczos 插值的计算量更大。
Lanczos 插值可能会产生轻微的振铃效应，尤其是在图像放大边缘处。

3. OpenCV 中的 resize() 函数使用示例

OpenCV 封装好了很多图像缩放方法的算法。在 OpenCV C++ 中的 resize() 函数用于调整图像大小，它可以根据指定的尺寸和插值方法对图像进行缩放。

cpp

代码解读

复制代码

void resize( InputArray src, OutputArray dst, Size dsize, double fx = 0, double fy = 0, int interpolation = INTER_LINEAR );

第四个参数 fx: 缩放比例，沿 x 轴的缩放因子。第五个参数 fx: 缩放比例，沿 y 轴的缩放因子。第六个参数 interpolation: 插值方法，常用的插值方法包括：

INTER_NEAREST: 最近邻插值
INTER_LINEAR: 双线性插值
INTER_CUBIC: 4*4 邻域双三次样条插值
INTER_AREA: 区域插值
INTER_LANCZOS4: 8*8 邻域 Lanczos 插值

作者：Tony沈哲
链接：https://juejin.cn/post/7338330579154059314
来源：稀土掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

双三次插值介绍
之前我写的这篇博客中讲了什么是超分，并实现了单线性插值算法和双线性插值算法。在这里将再介绍一种插值算法——双三次插值算法。

首先，双三次插值法需要参考16个点（4x4），因此插值效果会比双线性插值法要好，但同时时间开销也会更大。在 OpenCV 中，可在 cv::resize 函数中使用 cv::INTER_CUBIC 选项选择使用双三次插值算法改变图像大小。

在学习的过程中，我参考了这篇博客，其中的插值算法写成表达式的形式为：f ( x , y ) = ∑ i = 0 3

其中，(x,y) 表示待插值的像素点的坐标，f(x,y)表示经过计算待插值像素点应该插入的值，( x i , y j ) (x_i,y_j)(x
i

,y
j

) i , j = 0 , 1 , 2 , 3 i,j=0,1,2,3i,j=0,1,2,3 表示待插值点附近的 4x4 领域的点。

W WW函数称为 BiCubic 函数。与该博客中不同的是，原博客中的像素点可以是浮点数，而在 OpenCV 中坐标只能为整数。因此在这里 W WW 函数需要做个变换。

原博客中的 W WW 函数：

在这里使用的 W WW 函数：

其中 t tt 为超分放大倍数，a aa 为指定的值，OpenCV 源码中给的是 -0.75。

代码实现
首先是需要循环遍历每个像素点，逐个计算像素点的值。

进一步地，如何计算像素点的值呢？例如，下图中绿色的点是原图像上的像素点，红色的点是待计算的点，则用黄色框起来的点为参考的像素点。假设其坐标为(i,j)（在dst上，即保存超分结果的图像上），以行为例，则参考src的行号如下图所标注。对于列也是同理。因此我们知道了上述表达式中 x i x_ix
i

和 y j y_jy
j

的所有取值。

W ( x − x i ) W(x-x_i)W(x−x
i

) 中的 x − x i x-x_ix−x
i

表示当前像素点距离参考像素点的 x xx 方向上的距离（y yy 方向同理）。根据 W WW 函数的表达式可以判断出，这个距离应该要小于两倍的 t i m e s timestimes （放大倍数）。以左边的参考点为例（向右也是同理），在dst 图像中，对于离待计算点最近的左边的像素点，它们的 x xx 方向上的距离为 i % t i m e s i\%timesi%times 。又因为在 dst 图中，两个绿色的点之间的间距为放大倍数，因此计算点离最左边的参考点的距离为 i % t i m e s + t i m e s i\%times+timesi%times+times。同时考虑到右侧的点，可以写成更加一般的形式：i % t i m e s − i ∗ t i m e s i\%times-i*timesi%times−i∗times。其中 i = − 1 , 0 , 1 , 2 i=-1,0,1,2i=−1,0,1,2 。对于列也是同理。

(注：在代码中，为了与逐个枚举像素点的循环变量区分开，此处的 i j 会写成 r c。其中 r 代表 row，表示行； c 代表 col，表示列。)

以下是完整的代码：

//权重计算函数
//输入：x:自变量的值  times: 图片超分倍数
//返回值：W(x)计算之后的值
double W(int x,int times){
    
    x=std::abs(x);

    //OpenCV 中给的是 -0.75
    double a=-0.75;
    double abs_=std::abs((double)x/(double)times);
    
    if(x>=2*times) return 0.0;
    else if(x>times){
        double ans=a*(abs_)*(abs_)*(abs_)-5*a*(abs_)*(abs_)+8*a*(abs_)-4*a;
        return ans;
    }
    else{
        double ans=(a+2)*(abs_)*(abs_)*(abs_)-(a+3)*(abs_)*(abs_)+1;
        return ans;
    }

    //不会执行到这里的，哈哈
    return -1.0f;
}

//双三次插值
//输入：原图像（单通道），超分倍数
//返回值：超分后的图像
cv::Mat biCubicInterp(const cv::Mat &src, int times){
    cv::Mat dst=cv::Mat::zeros(cv::Size(src.cols*times,src.rows*times),CV_8UC1);

    for(int i=0;i<dst.rows;i++){
        for(int j=0;j<dst.cols;j++){
            double val=0.0;

            //利用周围16个像素点计算插值
            for(int r=-1;r<=2;r++){
                //如果参考点超出图像范围，则舍弃
                if(i/times+r<0 || i/times+r>=src.rows) continue;
                
                for(int c=-1;c<=2;c++){
                    //如果参考点超出图像范围，则舍弃
                    if(j/times+c<0 || j/times+c>=src.cols) continue;
                    
                    val+=(src.at<uchar>(i/times+r,j/times+c)*W(i%times-r*times,times)*W(j%times-c*times,times));
                }
            }

            //防止越界溢出
            if(val>255) val=255;
            if(val<0) val=-val;
            
            dst.at<uchar>(i,j)=(unsigned char)val;
        }
    }
    return dst;
}

运行结果
对一张 100x100 分辨率的图片，分别用双线性插值法和双三次插值法放大8倍，处理成 800x800 分辨率的图片。运行结果如下：

双线性插值法：