之前讲过ID3和C4.5决策树,CART和他们的区别虽然不大,但还是有一些值得说明的区别:
1 CART节点分支只能是两个,就是说二分,对于连续型feature,那么就和C4.5的方法一样,选取最优的分界。如果是离散型feature,那么我们想要分成两部分,就显得比较复杂,比如说1,2,3分成两部分,可以是{1,2},{3}和{1,3},{2},{2,3},{1}。这里可以说一个公式,n个属性,可以分出(2^n-2)/2种情况。
2 CART既可以是分类树,也可以是回归树。我现在看到的ID3和C4.5都是用来分类的,并没有看到他们用来回归,但是CART可以用来回归,那么这里就涉及到一个计算问题,如何衡量混乱度。这也是要说的第三个区别。
3 对于分类树,CART选用了一个叫做gini指数来衡量复杂度,其计算方式如下:
其中Pj表示每一类所占的比例,如果都是同一类那么显然gini=0,也就是混乱度最低。分完类后的gini计算方式如下:
我们的目标就是求得gini(T)-ginisplit(t)最大的分裂方法。
而对于回归树,CART一般选择的是方差来衡量,就是我们枚举特征后求出两个类别的方差和,选择使得方差和最小(或者说分裂前后方差差值最大)的分裂方法。
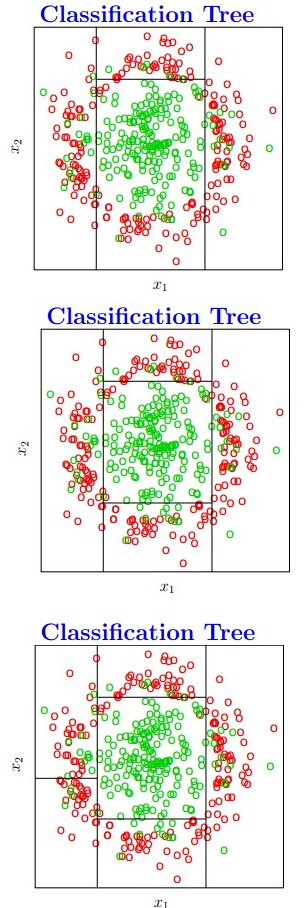
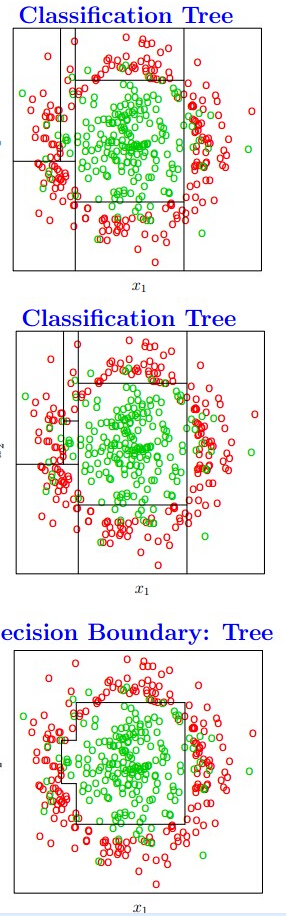
这里附上几幅图帮助理解:
从这几幅图可以发现,CART 有一个和其他2个决策树不一样的地方就是某个feature可以被划分好多次,且每次都是分成2部分,值得注意的一点是,虽然分成2部分,但是分之前的属性取值和之前分的不一样。
然后讨论下决策树的2个剪枝理论:
1 REP剪枝:
这个剪枝法思想非常的简单,但是需要一个用了测试的数据集,因为我们怀疑我们根据样本所建的决策树会过拟合,那么现在我们就找另外一个数据集来检验下,对于任何一个非叶子节点(注意这个剪枝是从下往上的),用叶子节点代替它,该叶子节点的类别我们用子树所覆盖训练样本中存在最多的那个类来代替,然后比较剪枝前后的两棵树在测试数据集上的效果,如果用叶子节点代替后错误率更低,那么就用叶子节点代替。
2 PEP剪枝:
这个剪枝也叫做悲观剪枝法,其实和第一种差不多,主要区别就是衡量错误率,对于一颗叶子节点,它覆盖了N个样本,其中有E个错误,那么该叶子节点的错误率为(E+0.5)/N,这个0.5是惩罚因子,那么一颗子树,它有L个叶子节点,那么该子树的误判率估计为:
另外剪掉后变成一个叶子节点错误率计算也要加上0.5惩罚因子,之后假设这个错误率满足一个比如二项分布或者正太分布,然后分别估计剪枝前的错误次数E(subtree_err_count)和标准差V(subtree_err_count)和剪枝后的错误次数E(leaf_err_count),那么在符合:
就会执行剪枝。












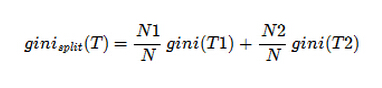

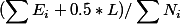
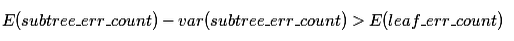
















 2313
2313

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








