光线与包围盒（AABB）的相交检测算法

这里介绍两种算法，第一种比较容易理解

下面是Cocos2dx中实现Ray-AABB相交（碰撞）检测的算法，说明看注释

bool Ray::intersects(const AABB& aabb) const
{
  Vec3 ptOnPlane; //射线与包围盒某面的交点
  Vec3 min = aabb._min; //aabb包围盒最小点坐标
  Vec3 max = aabb._max; //aabb包围盒最大点坐标
  
  const Vec3& origin = _origin; //射线起始点
  const Vec3& dir = _direction; //方向矢量
  
  float t;
  
  //分别判断射线与各面的相交情况
  
  //判断射线与包围盒x轴方向的面是否有交点
  if (dir.x != 0.f) //射线x轴方向分量不为0 若射线方向矢量的x轴分量为0，射线不可能经过包围盒朝x轴方向的两个面
  {
    /*
      使用射线与平面相交的公式求交点
     */
    if (dir.x > 0)//若射线沿x轴正方向偏移
      t = (min.x - origin.x) / dir.x;
    else  //射线沿x轴负方向偏移
      t = (max.x - origin.x) / dir.x;
    
    if (t > 0.f) //t>0时则射线与平面相交
    {
      ptOnPlane = origin + t * dir; //计算交点坐标
      //判断交点是否在当前面内
      if (min.y < ptOnPlane.y && ptOnPlane.y < max.y && min.z < ptOnPlane.z && ptOnPlane.z < max.z)
      {
        return true; //射线与包围盒有交点
      }
    }
  }
  
  //若射线沿y轴方向有分量 判断是否与包围盒y轴方向有交点
  if (dir.y != 0.f)
  {
    if (dir.y > 0)
      t = (min.y - origin.y) / dir.y;
    else
      t = (max.y - origin.y) / dir.y;
    
    if (t > 0.f)
    {
      ptOnPlane = origin + t * dir;

      if (min.z < ptOnPlane.z && ptOnPlane.z < max.z && min.x < ptOnPlane.x && ptOnPlane.x < max.x)
      {
        return true;
      }
    }
  }
  
  //若射线沿z轴方向有分量 判断是否与包围盒y轴方向有交点
  if (dir.z != 0.f)
  {
    if (dir.z > 0)
      t = (min.z - origin.z) / dir.z;
    else
      t = (max.z - origin.z) / dir.z;
    
    if (t > 0.f)
    {
      ptOnPlane = origin + t * dir;
      
      if (min.x < ptOnPlane.x && ptOnPlane.x < max.x && min.y < ptOnPlane.y && ptOnPlane.y < max.y)
      {
        return true;
      }
    }
  }
  
  return false;
}

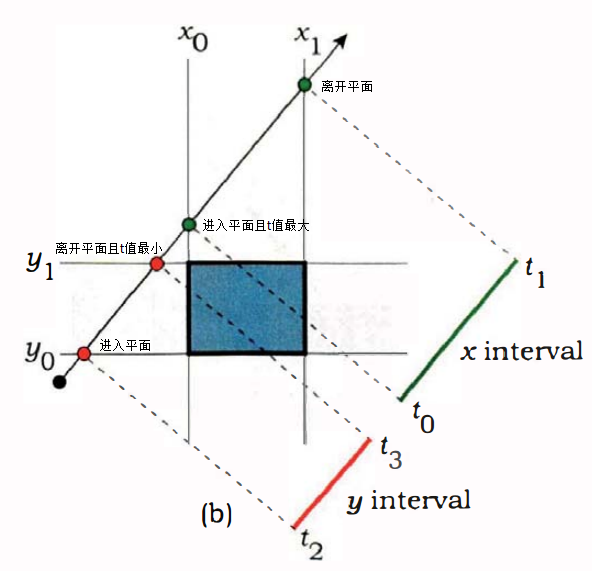
下面是另外一种Ray-AABB检测算法，称为"Slabs method"

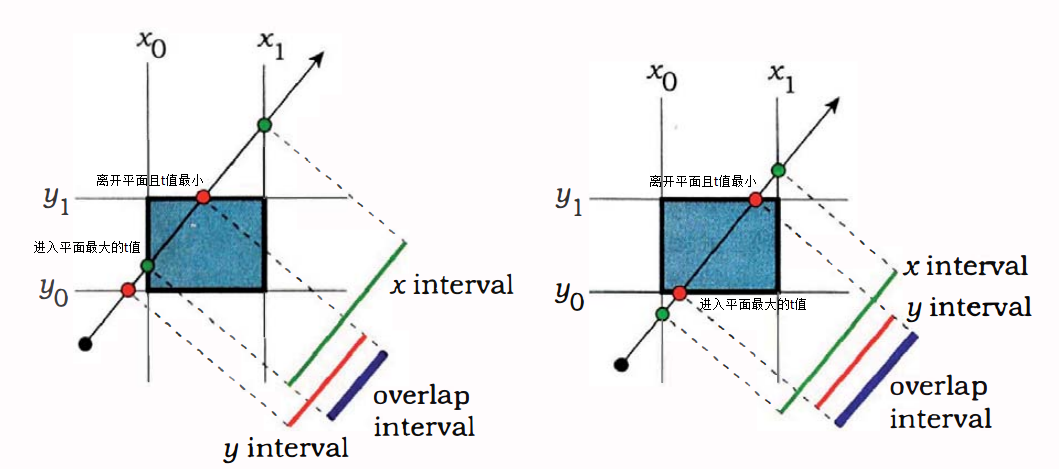
观察上述三幅图可以得出，只要发生区间交叠，光线与平面就能相交，

那么区间交叠出现的条件便是：光线进入平面处的最大t值小于光线离开平面处的最小t值

那么问题就变成了如何求 光线进入平面处的最大t值 以及 光线离开平面处的最小t值

这个问题很简单，通过光线与平面相交的参数方程求解就可以了，

光线的参数方程为R(t) = O + t * Dir

一般平面方程为aX+bY+cZ+d=0，因为AABB的六个面分别平行于XY、XZ、YZ平面，所以平面的方程为X=d，Y=d，Z=d

光线与垂直于x轴的两个面相交时，t = (d - O.x) / Dir.x
光线与垂直于y轴的两个面相交时，t = (d - O.y) / Dir.y
光线与垂直于z轴的两个面相交时，t = (d - O.z) / Dir.z

注意到t<0时，交点位于光线的起点之后，则光线（射线）并未与盒体发生相交

bool BBox::hit(const Ray& ray) const
{
	double ox = ray.o.x;double oy = ray.o.y;double oz = ray.o.z;
	double dx = ray.d.x;double dy = ray.d.y;double dz = ray.d.z;
	double tx_min,ty_min,tz_min;
	double tx_max,ty_max,tz_max;

	//x0,y0,z0为包围体的最小顶点
	//x1,y1,z1为包围体的最大顶点
	if(abs(dx) < 0.000001f) 
	{
		//若射线方向矢量的x轴分量为0且原点不在盒体内
		if(ox < x1 || ox > x0)
			return false ;
	}
	else
	{
		if(dx>=0)
		{
			tx_min = (x0-ox)/dx;
			tx_max = (x1-ox)/dx;
		}
		else
		{
			tx_min = (x1-ox)/dx;
			tx_max = (x0-ox)/dx;
		}

	}

	
	if(abs(dy) < 0.000001f) 
	{
		//若射线方向矢量的x轴分量为0且原点不在盒体内
		if(oy < y1 || oy > y0)
			return false ;
	}
	else
	{
		if(dy>=0)
		{
			ty_min = (y0-oy)/dy;
			ty_max = (y1-oy)/dy;
		}
		else
		{
			ty_min = (y1-oy)/dy;
			ty_max = (y0-oy)/dy;
		}

	}

	
	if(abs(dz) < 0.000001f) 
	{
		//若射线方向矢量的x轴分量为0且原点不在盒体内
		if(oz < z1 || oz > z0)
			return false ;
	}
	else
	{
		if(dz>=0)
		{
			tz_min = (z0-oz)/dz;
			tz_max = (z1-oz)/dz;
		}
		else
		{
			tz_min = (z1-oz)/dz;
			tz_max = (z0-oz)/dz;
		}

	}

	double t0,t1;
	
	//光线进入平面处（最靠近的平面）的最大t值 
	t0=max(tz_min,max(tx_min,ty_min));
	
	//光线离开平面处（最远离的平面）的最小t值
	t1=min(tz_max,min(tx_max,ty_max));
	
	return t0<t1;
}