CLRS 14.1动态顺序统计

最新推荐文章于 2018-08-24 18:34:03 发布

昵称怎么会存在

最新推荐文章于 2018-08-24 18:34:03 发布

阅读量459

点赞数

分类专栏：算法导论文章标签： clrs 动态顺序统计

本文链接：https://blog.csdn.net/u012593447/article/details/48751305

版权

算法导论专栏收录该内容

84 篇文章 10 订阅

订阅专栏

14.1-1
不画图，直接描述访问的关键字分别是（关键字后面括号的内容是 $x.left.size+1$ 和 $i$ ）：
26（12+1 > 10），17（7+1 < 10），21（2+1 > 2（注意此时的 $i$ 变了）），19（0+1 < 2），20（1 == 1）

14.1-2
第一次迭代： $y.key=35,r=1$ ；
第二次迭代： $y.key=38,r=3$ ；
第三次迭代： $y.key=30,r=3$ ；
第四次迭代： $y.key=41,r=16$ ；

14.1-3
见练习 14.1-8 下面的代码non_recursion_SELECT部分。

14.1-4
见练习 14.1-8 下面的代码OS_RANK部分。

14.1-5
先求出元素 $x$ 的秩 $r$ ，再求出 $r+i$ 的元素即可。由于OS_RANK和OS_SELECT都只是 $O(\lg n)$ ，因此满足题意。

OS-SUCCESSOR(T, x, i )
    r = OS-RANK(T, x)
    s = r + i
    return OS-SELECT(T.root, s)

14.1-6
当插入一个结点 $z$ 时，我们从根结点开始向下搜索结点 $z$ 需要插入的位置，在搜索路径中的每个结点 $x$ ，若结点 $z$ 插入在 $x$ 的左子树，则 $x.rank$ 加 1，否则 $x.rank$ 不变。删除则同理，当被删除的 $z$ 在结点 $x$ 的左子树时， $x.rank$ 减 1，否则 $x.rank$ 不变。
对于旋转操作，考虑一下左旋 $x$ ，旋转前 $x$ 的右孩子是 $y$ 并且 $r=y.rank$ ，旋转后， $x.rank$ 不变， $y.rank=r+x.rank$ 即可，对于右旋，情况类似。

14.1-7
对一个数组 $A[1...n]$ ，所有元素的逆序对总和为： $\sum \limits_{j=1}^{n}|Inv(j)|$ ，其中 $|Inv(j)|=\{i:i<j 并且A[i]>A[j]\}$ ，也就是排在 $j$ 前面且比 $A[j]$ 大的元素。
现在来观察 $|Inv(j)|$ ，它和子数组 $A[1..j]$ 有关，设 $r(j)$ 表示 $A[j]$ 在子数组 $A[1..j]$ 的秩，则有 $j=r(j)+|Inv(j)|$ 。举个例子，令 $j=5$ ，子数组 $A[1..5]$ 中比 $A[5]$ 大的有 3 个数，所以 $r(j)=2,|Inv(j)|=3,j=2+3$ 。
从而 $|Inv(j)|=j-r(j)$ 。所以我们每插入一个数，求出插入后这个数的秩，然后就可以得出此数的逆序对数。将所有的逆序对数相加即可得到总逆序对数。
插入一个数时间为 $O(\lg n)$ ，一个有 $n$ 个数，总的时间就是 $O(n\lg n)$ 。

14.1-8
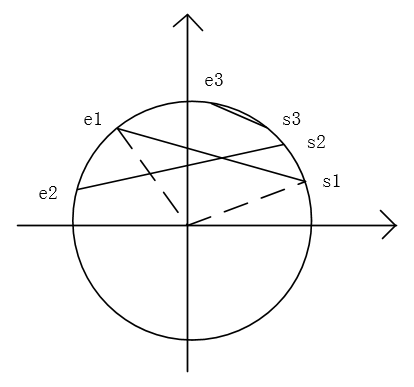
先考虑怎么判断弦相交。对于一个弦，它有两个端点 $S,E$ ，这两个端点分别和原点连线，分别取名为 $SO,EO$ ，以 $x$ 轴正反向、原点和 $SO$ 可以形成一个角，同理 $x$ 轴正反向、原点和 $EO$ 可以形成一个角（规定 $x$ 轴正反向、原点和 $SO$ 之间的夹角小于180度）。现在假设由两条弦 $S_1E_1,S_2E_2$ ，四个角 $S_1,E_1,S_2,E_2$ ，若 $S_1<S_2<E_1<E_2或者S_2<S_1<E_2<E_1$ 表示两弦相交。

这里写图片描述

接下来：

按照角度小到大的顺序遍历这2n个端点：
    如果该端点是某条弦X的“起点”
        将弦X插入顺序统计树中（以X的“起点”角度作为key）；
    如果该端点是某条弦X的“终点”
        统计出目前这棵树中有多少条弦的“起点”角度比X的“起点”角度大，这就是与X相交的弦的数量；
        将弦X从顺序统计树中删除；

这个问题类似的转化为了上一题的求逆序对，总的时间就是 $O(n\lg n)$ 。

附上红黑树的顺序统计量代码（代码看不懂的请看书上红黑树部分，基本都和书上的伪代码差不多）

#include <iostream>
#include <climits>
#include <iomanip>
using std::cout;
using std::endl;

enum COLOR
{
    RED = 0,BLACK = 1
};

struct OS_RB_TREE
{
    int key;
    int size;
    COLOR color;
    OS_RB_TREE *parent;
    OS_RB_TREE *left;
    OS_RB_TREE *right;
};

OS_RB_TREE nil = {INT_MIN,0,BLACK,NULL,NULL,NULL};//哨兵

void LEFT_ROTATE(OS_RB_TREE **root,OS_RB_TREE *x)
{
    if(x->right != &nil)
    {
        OS_RB_TREE *y = x->right;
        x->right = y->left;
        if(y->left != &nil)
            y->left->parent = x;
        y->parent = x->parent;
        if(x->parent == &nil)
            *root = y;
        else if(x == x->parent->left)
            x->parent->left = y;
        else x->parent->right = y;
        y->left = x;
        x->parent = y;
        y->size = x->size;     //更新size
        x->size = x->left->size + x->right->size + 1;
    }
}

void RIGHT_ROTATE(OS_RB_TREE **root,OS_RB_TREE *x)
{
    if(x->left != &nil)
    {
        OS_RB_TREE *y = x->left;
        x->left = y->right;
        if(y->right != &nil)
            y->right->parent = x;
        y->parent = x->parent;
        if(x->parent == &nil)
            *root = y;
        else if(x == x->parent->left)
            x->parent->left = y;
        else x->parent->right = y;
        y->right = x;
        x->parent = y;
        y->size = x->size;
        x->size = x->left->size + x->right->size + 1;
    }
}

OS_RB_TREE *SEARCH(OS_RB_TREE *root,int key)
{
    if(root == &nil || root->key == key)
        return root;
    else if(root->key > key)
        return SEARCH(root->left,key);
    else return SEARCH(root->right,key);
}

OS_RB_TREE *MINIMUM(OS_RB_TREE *x)
{
    if(x == &nil || x->left == &nil)
        return x;
    else return MINIMUM(x->left);
}

OS_RB_TREE *MAXIMUM(OS_RB_TREE *x)
{
    if(x == &nil || x->right == &nil)
        return x;
    else return MAXIMUM(x->right);
}

OS_RB_TREE *SUCCESSOR(OS_RB_TREE *x)
{
    if(x == &nil)
        return x;
    if(x->right != &nil)
        return MINIMUM(x->right);
    OS_RB_TREE *y = x->parent;
    while(y != &nil && x == y->right)
    {
        x = y;
        y = y->parent;
    }
    return y;
}

OS_RB_TREE *PREDECESSOR(OS_RB_TREE *x)
{
    if(x == &nil)
        return x;
    if(x->left != &nil)
        return MAXIMUM(x->left);
    OS_RB_TREE *y = x->parent;
    while(y != &nil && x == y->left)
    {
        x = y;
        y = y->parent;
    }
    return y;
}

void OS_RB_TREE_INSERT_FIXUP(OS_RB_TREE **root,OS_RB_TREE *z)
{
    while(z->parent->color == RED)
    {
        if(z->parent == z->parent->parent->left)
        {
            OS_RB_TREE *y = z->parent->parent->right;
            if(y->color == RED)
            {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;
                z = z->parent->parent;
            }
            else
            {
                if(z == z->parent->right)
                {
                    z = z->parent;
                    LEFT_ROTATE(root,z);
                }
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                RIGHT_ROTATE(root,z->parent->parent);
            }
        }
        else
        {
            OS_RB_TREE *y = z->parent->parent->left;
            if(y->color == RED)
            {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;
                z = z->parent->parent;
            }
            else
            {
                if(z == z->parent->left)
                {
                    z = z->parent;
                    RIGHT_ROTATE(root,z);
                }
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                LEFT_ROTATE(root,z->parent->parent);
            }
        }
    }
    (*root)->color = BLACK;
}

void OS_RB_TREE_INSERT(OS_RB_TREE **root,int key)
{
    OS_RB_TREE *y = &nil;
    OS_RB_TREE *x = *root;
    while(x != &nil)
    {
        y = x;
        y->size += 1;   //根到插入结点路径上每个结点size都加1
        if(x->key > key)
            x = x->left;
        else x = x->right;
    }
    OS_RB_TREE *z = new OS_RB_TREE;
    z->parent = y;
    if(y == &nil)
        *root = z;
    else if(key < y->key)
        y->left = z;
    else y->right = z;
    z->key = key;
    z->size = 1;
    z->left = z->right = &nil;
    z->color = RED;
    OS_RB_TREE_INSERT_FIXUP(root,z);
}

void OS_RB_TREE_TRANSPLATE(OS_RB_TREE **root,OS_RB_TREE *u,OS_RB_TREE *v)
{
    if(u->parent == &nil)
        *root = v;
    else if(u == u->parent->left)
        u->parent->left = v;
    else u->parent->right = v;
    v->parent = u->parent;
}

void OS_RB_TREE_DELETE_FIXUP(OS_RB_TREE **root,OS_RB_TREE *x)
{
    while(x != *root && x->color == BLACK)
    {
        if(x == x->parent->left)
        {
            OS_RB_TREE *w = x->parent->right;
            if(w->color == RED)
            {
                w->color = BLACK;
                x->parent->color = RED;
                LEFT_ROTATE(root,x->parent);
                w = x->parent->right;
            }
            if(w->left->color == BLACK && w->right->color == BLACK)
            {
                w->color = RED;
                x = x->parent;
            }
            else
            {
                if(w->right->color == BLACK)
                {
                    w->left->color = BLACK;
                    w->color = RED;
                    RIGHT_ROTATE(root,w);
                    w = x->parent->right;
                }
                w->color = x->parent->color;
                x->parent->color = BLACK;
                w->right->color = BLACK;
                LEFT_ROTATE(root,x->parent);
                x = *root;
            }
        }
        else
        {
            OS_RB_TREE *w = x->parent->left;
            if(w->color == RED)
            {
                w->color = BLACK;
                x->parent->color = RED;
                RIGHT_ROTATE(root,x->parent);
                w = x->parent->left;
            }
            if(w->left->color == BLACK && w->right->color == BLACK)
            {
                w->color = RED;
                x = x->parent;
            }
            else
            {
                if(w->left->color == BLACK)
                {
                    w->right->color = BLACK;
                    w->color = RED;
                    LEFT_ROTATE(root,w);
                    w = x->parent->left;
                }
                w->color = x->parent->color;
                x->parent->color = BLACK;
                w->left->color = BLACK;
                RIGHT_ROTATE(root,x->parent);
                x = *root;
            }
        }
    }
    x->color = BLACK;
}

void OS_RB_TREE_DELETE(OS_RB_TREE **root,int key)
{
    OS_RB_TREE *z = SEARCH(*root,key);
    if(z == &nil)
        return;
    OS_RB_TREE *y = z;
    COLOR y_original_color = y->color;
    OS_RB_TREE *x;
    if(z->left == &nil)
    {
        x = z->right;
        OS_RB_TREE_TRANSPLATE(root,z,z->right);
        OS_RB_TREE *parent = z->parent;
        while(parent != &nil)   //祖先结点的size都减1
        {
            parent->size -= 1;
            parent = parent->parent;
        }
    }
    else if(z->right == &nil)
    {
        x = z->left;
        OS_RB_TREE_TRANSPLATE(root,z,z->left);
        OS_RB_TREE *parent = z->parent;
        while(parent != &nil)
        {
            parent->size -= 1;
            parent = parent->parent;
        }
    }
    else
    {
        y = MINIMUM(z->right);
        y_original_color = y->color;

        OS_RB_TREE *parent = y->parent;
        while(parent != &nil)
        {
            parent->size -= 1;
            parent = parent->parent;
        }

        x = y->right;
        if(y->parent == z)
            x->parent = y;
        else
        {
            OS_RB_TREE_TRANSPLATE(root,y,y->right);
            y->right = z->right;
            y->right->parent = y;
        }
        OS_RB_TREE_TRANSPLATE(root,z,y);
        y->left = z->left;
        y->left->parent = y;
        y->color = z->color;
    }
    if(y_original_color == BLACK)
        OS_RB_TREE_DELETE_FIXUP(root,x);
    delete z;
}

OS_RB_TREE *SELECT(OS_RB_TREE *x,int i)
{
    int r = x->left->size + 1;
    if(i == r)
        return x;
    else if(i < r)
        return SELECT(x->left,i);
    else return SELECT(x->right,i-r);
}

OS_RB_TREE *non_recursion_SELECT(OS_RB_TREE *x,int i)
{
    int r = x->left->size + 1;
    while(r != i)
    {
        if(i < r)
        {
            x = x->left;
            r = x->left->size + 1;
        }
        else
        {
            x = x->right;
            i -= r;
            r = x->left->size + 1;
        }
    }
    return x;
}

int OS_RANK(OS_RB_TREE *root,int key)
{
    if(key == root->key)
        return root->left->size + 1;
    else if(key < root->key)
        return OS_RANK(root->left,key);
    else return OS_RANK(root->right,key) + root->left->size + 1;
}

int non_recursion_OS_RANK(OS_RB_TREE *root,OS_RB_TREE *x)
{
    int r = x->left->size + 1;
    OS_RB_TREE *y = x;
    while(y != root)
    {
        if(y == y->parent->right)
            r += y->parent->left->size + 1;
        y = y->parent;
    }
    return r;
}

void preOrder(OS_RB_TREE *root)
{
    if(root != &nil)
    {
        cout << "key is: " << std::setw(3) << root->key << " it's size is:"  << root->size << " and color is: ";
        if(root->color == BLACK)
            cout << "BLACK" << endl;
        else cout << "RED" << endl;
        preOrder(root->left);
        preOrder(root->right);
    }
}

void inOrder(OS_RB_TREE *root)
{
    if(root != &nil)
    {
        inOrder(root->left);
        cout << "key is: " << std::setw(3) << root->key << " it's size is:"  << root->size << " and color is: ";
        if(root->color == BLACK)
            cout << "BLACK" << endl;
        else cout << "RED" << endl;
        inOrder(root->right);
    }
}

void postOrder(OS_RB_TREE *root)
{
    if(root != &nil)
    {
        postOrder(root->left);
        postOrder(root->right);
        cout << "key is: " << std::setw(3) << root->key << " it's size is:"  << root->size << " and color is: ";
        if(root->color == BLACK)
            cout << "BLACK" << endl;
        else cout << "RED" << endl;
    }
}

int main()
{
    int ia[] = {41,38,31,12,19,8};
    OS_RB_TREE *root = &nil;
    for(int i = 0; i < 6; ++i)                 //创建红黑树
        OS_RB_TREE_INSERT(&root,ia[i]);

    cout << "preOder is" << endl;
    preOrder(root);
    cout << endl;
    cout << "inOder is" << endl;
    inOrder(root);
    cout << endl;
    cout << "postOder is" << endl;
    postOrder(root);
    cout << endl;

    int i = 4;                                 //第i小的元素
    OS_RB_TREE *x = SELECT(root,i);
    if(x != &nil)
    {
        int r = non_recursion_OS_RANK(root,x);
        cout << "The " << i << "th smallest is: " << x->key << " and rank is: " << r << endl;
    }
    else cout << "no this element" << endl;
    cout << endl;

    OS_RB_TREE_DELETE(&root,8);              //删除关键字8的结点
    cout << "after delete key 8:" << endl;
    cout << "preOder is" << endl;
    preOrder(root);
    cout << endl;
    cout << "inOder is" << endl;
    inOrder(root);
    cout << endl;
    cout << "postOder is" << endl;
    postOrder(root);
    cout << endl;

    OS_RB_TREE_DELETE(&root,12);             //删除关键字12的结点
    cout << "after delete key 12:" << endl;
    cout << "preOder is" << endl;
    preOrder(root);
    cout << endl;
    cout << "inOder is" << endl;
    inOrder(root);
    cout << endl;
    cout << "postOder is" << endl;
    postOrder(root);
    cout << endl;

    OS_RB_TREE_DELETE(&root,19);              //删除关键字19的结点
    cout << "after delete key 19:" << endl;
    cout << "preOder is" << endl;
    preOrder(root);
    cout << endl;
    cout << "inOder is" << endl;
    inOrder(root);
    cout << endl;
    cout << "postOder is" << endl;
    postOrder(root);

    cout << endl;
    return 0;
}