(图片例子来自上课时老师的PPT,不过老师说PPT是他从网上组合的,所以没有出处)
1、Partial-Mapped Crossover (PMX)
过程:
过程:
第一步,随机选择一对染色体(父代)中几个基因的起止位置(两染色体被选位置相同):

第二步,交换这两组基因的位置:
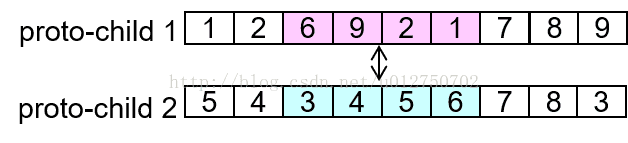
第三步,做冲突检测,根据交换的两组基因建立一个映射关系,如图所示,以1-6-3这一映射关系为例,可以看到第二步结果中子代1存在两个基因1,这时将其通过映射关系转变为基因3,以此类推至没有冲突为止。最后所有冲突的基因都会经过映射,保证形成的新一对子代基因无冲突:

最终结果:

2、Order Crossover (OX)
过程:
第一步,与PMX相同,随机选择一对染色体(父代)中几个基因的起止位置(两染色体被选位置相同):
过程:
第一步,与PMX相同,随机选择一对染色体(父代)中几个基因的起止位置(两染色体被选位置相同):

第二步,生成一个子代,并保证子代中被选中的基因的位置与父代相同:

第三步(可再分两小步),先找出第一步选中的基因在另一个父代中的位置,再将其余基因按顺序放入上一步生成的子代中:

需要注意的是,这种算法同样会生成两个子代,另一个子代生成过程完全相同,只需要将两个父代染色体交换位置,第一步选中的基因型位置相同,本例中的另一个子代为:254913678
与PMX不同的是,不用进行冲突检测工作(实际上也只有PMX需要做冲突检测)。
3、Position-based Crossover (PBX)
过程:
第一步,随机选择一对染色体(父代)中几个基因,位置可不连续,但两染色体被选位置相同:
与PMX不同的是,不用进行冲突检测工作(实际上也只有PMX需要做冲突检测)。
3、Position-based Crossover (PBX)
过程:
第一步,随机选择一对染色体(父代)中几个基因,位置可不连续,但两染色体被选位置相同:

第二步,与OX的第二步相同,生成一个子代,并保证子代中被选中的基因的位置与父代相同:

第三步,也与OX的第三步相同,先找出第一步选中的基因在另一个父代中的位置,再将其余基因按顺序放入上一步生成的子代中:

与上俩个算法不同的是,选择的基因型位置可以不连续,出来这一点外与OX基本一致,同样有两个子代,本例的另一个为:243519678。
4、Order-Based Crossover (OBX)
过程:
第一步,随机选择一对染色体(父代)中几个基因,位置可不连续,但两染色体被选位置相同:

第二步(分为两小步),先在父代2中找到父代1被选中基因的位置,再用父代2中其余的基因生成子代,并保证位置对应:

第三步,将父代1中被选择的基因按顺序放入子代剩余位置中:
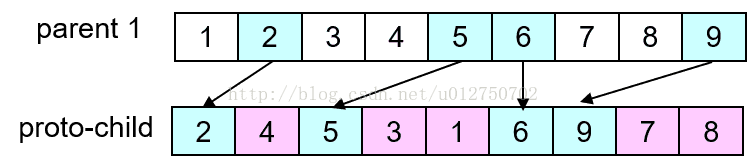
同理,交换父代1、2可得到另一个子代(被选择基因的位置不变),本例结果为:423156798。
OBX与PBX相比生成子代的“基础”基因来源不同一个来自被选中基因,一个来自剩余的,此外思想基本相似。
5、Cycle Crossover (CX)
过程:
第一步,在某个父代上随机选择1个基因,然后找到另一个父代相应位置上的基因编号,再回到第一个父代找到同编号的基因的位置,重复先前工作,直至形成一个环,环中的所有基因的位置即为最后选中的位置:
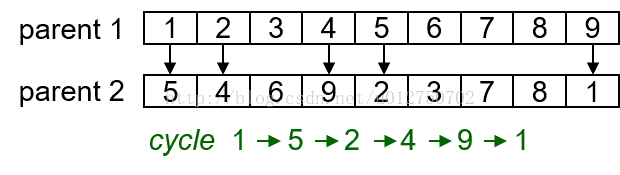
第二步,用父代1中选中的基因生成子代,并保证位置对应:

第三步,将父代2中剩余基因放入子代中:
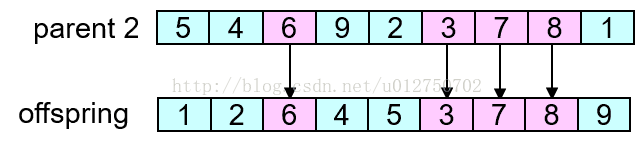
与上述算法不同的是,仅需要在一个染色体上随机选择一个位置;本例另一个子代结果为:543926781。
6、Subtour Exchange Crossover
过程:
第一步,在某个父代上选择1组基因,在另一父代上找到这些基因的位置:
过程:
第一步,在某个父代上选择1组基因,在另一父代上找到这些基因的位置:

第二步,保持未选中基因不变,按选中基因的出现顺序,交换两父代染色体中基因的位置,一次生成两个子代:

与上述算法不同的是,只在一个染色体上选择基因的位置。






















 2846
2846

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








