逻辑回归 — Logistic Regression

逻辑回归通式定义如下：
$$\{\begin{array}{l}p(z_i)=\frac{1}{1+e^{-z_i}}\\ z_i={\theta }^T{x}_i\end{array}$$

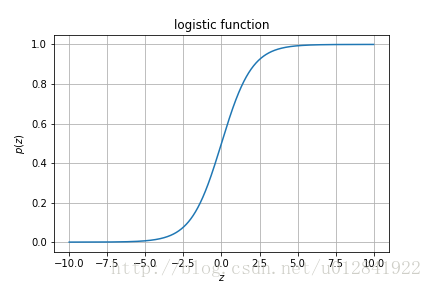
要想理解逻辑回归，我们需要看一下函数$p$的图像，如下图：

由图可知，在$z\in R$的定义域中，函数$p$将$z$映射到$(0,1)$的值域中，其中$z=0$时，$p(z)=0.5$。一种常见的对这个图的解释是$p(x_i;\theta )=\frac{1}{1+e^{-{\theta }^T{x}_i}}$是事件$x_i$发生的概率。

事件$x_i$发生与否其实也就是一个二分类问题。我们可以用标签$y_i=1$表示事件$x_i$发生，标签$y_i=0$表示事件$x_i$不发生。用函数$p(x;\theta )$表示事件$x$发生的概率$Pr(Y=1|X=x)$。因此，事件$x$不发生的概率$Pr(Y=0|X=x)$为$1-p(x;\theta )$。我们可以用一个式子表示如上两种情况：
$$Pr(Y=y_i|X=x_i)=p(x_i;\theta {)}^{y_i}(1-p(x_i;\theta ){)}^{1-y_i}$$

从现在开始，我们应该对逻辑回归有了初步的认识。逻辑回归是一个分类算法，而非回归算法。本文主要分析其在二分类问题中的应用。逻辑回归以概率的方式来对数据进行分类。例如，设置阈值为$0.5$，如果$Pr(Y=1|X=x_i)\ge 0.5$，则将数据$x_i$标记为类$1$，否则将其标记为类$0$。$p(x_i;\theta )=0.5$其实就是一个超平面，平面之上的点组成$y_i=1$的集合，平面之下的点组成$y_i=0$的集合。总结一下我们的问题：已知$x_i$和$y_i$，求函数$p(x_i;\theta )$中的$\theta$的取值。

首先，我先给出此问题的似然函数：
$$\prod _{i=1}^{m}Pr(Y=y_i|X=x_i)$$

为了理解这个最大似然估计函数，我们考虑一个简单的、却类似的问题。假设一个袋子里有若干颗白球和黑球，在10次有放回的抽取中，我抽到了8次黑球，2次白球。如何求袋子中黑白球的比例呢？我们可以利用最大似然估计：假设我抽取到黑球的概率为$p$，那么我这次抽取得到8次黑球、2次白球的概率为：
$$P=p^8\ast (1-p{)}^2$$

我们用使这次抽取结果发生的概率$P$最大化的$\hat{p}$值去近似替代实际的$p$值。

同样的道理，回到逻辑回归的问题中。我们要目前已知的标签集合$Y$发生的概率最大化，求该情况下的$\theta$的取值。因此：
$$L(\theta )=\prod _{i=1}^{m}Pr(Y=y_i|X=x_i)=\prod _{i=1}^{m}p(x_i;\theta {)}^{y_i}(1-p(x_i;\theta ){)}^{1-y_i}$$

对数似然函数为：
$$\begin{array}{rl}& l(\theta )=\log (L(\theta ))=\sum _{i=1}^m\log [p(x_i;\theta {)}^{y_i}(1-p(x_i;\theta ){)}^{1-y_i}]\\ & =\sum _{i=1}^m[y_i\log p(x_i)+(1-y_i)\log (1-p(x_i))]\\ & =\sum _{i=1}^m[\log (1-p(x_i))+y_i(\log p(x_i)-\log (1-p(x_i)))]\\ & =\sum _{i=1}^m[\log (1-p(x_i))+y_i\log \frac{p(x_i)}{1-p(x_i)}]\\ & =\sum _{i=1}^m[\log (1-\frac{1}{1+e^{-{\theta }^T{x}_i}})+y_i\log \frac{(1+e^{-{\theta }^T{x}_i}{)}^{-1}}{1-(1+e^{-{\theta }^T{x}_i}{)}^{-1}}]\\ & =\sum _{i=1}^m[\log \frac{e^{-{\theta }^T{x}_i}}{1+e^{-{\theta }^T{x}_i}}+y_i\log \frac{1}{(1+e^{-{\theta }^T{x}_i})-1}]\\ & =\sum _{i=1}^m[\log \frac{1}{e^{{\theta }^T{x}_i}+1}+y_i\log e^{{\theta }^T{x}_i}]\\ & =\sum _{i=1}^m-\log (e^{{\theta }^T{x}_i}+1)+\sum _{i=1}^m{y}_i{\theta }^T{x}_i\end{array}$$

求$l(\theta )$对${\theta }_j$的偏导数：
$$\begin{array}{rl}& \frac{\partial l(\theta )}{\partial {\theta }_j}=\frac{\partial }{{\theta }_j}[\sum _{i=1}^m-\log (e^{{\theta }^T{x}_i}+1)+\sum _{i=1}^m{y}_i{\theta }^T{x}_i]\\ & =\sum _{i=1}^m-\frac{e^{{\theta }^T{x}_i}{x}_i^j}{1+e^{{\theta }^T{x}_i}}+\sum _{i=1}^m{y}_i{x}_i^j\\ & =\sum _{i=1}^m[y_i-\frac{e^{{\theta }^T{x}_i}}{1+e^{{\theta }^T{x}_i}}]x_i^j\\ & =\sum _{i=1}^m[y_i-\frac{1}{1+e^{-{\theta }^T{x}_i}}]x_i^j\\ & =\sum _{i=1}^m[y_i-p(x_i;\theta )]x_i^j\end{array}$$

最后，通过梯度上升求$l(\theta )$最大化时$\theta$的近似解：
$${\theta }_j:={\theta }_j+\alpha \frac{\partial l(\theta )}{\partial {\theta }_j}$$

将上式写成向量形式，即：$\theta =\theta +\alpha ▽l(\theta )$。