1. 背景介绍
火力发电的基本原理是:燃料在燃烧时加热水生成蒸汽,蒸汽压力推动汽轮机旋转,然后汽轮机带动发电机旋转,产生电能。在这一系列的能量转化中,影响发电效率的核心是锅炉的燃烧效率,即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多,包括锅炉的可调参数,如燃烧给量,一二次风,引风,返料风,给水水量;以及锅炉的工况,比如锅炉床温、床压,炉膛温度、压力,过热器的温度等。我们如何使用以上的信息,根据锅炉的工况,预测产生的蒸汽量,来为我国的工业届的产量预测贡献自己的一份力量呢?
所以,该案例是使用以上工业指标的特征,进行蒸汽量的预测问题。由于信息安全等原因,我们使用的是经脱敏后的锅炉传感器采集的数据(采集频率是分钟级别)。
数据信息
数据分成训练数据(train.txt)和测试数据(test.txt),其中字段”V0”-“V37”,这38个字段是作为特征变量,”target”作为目标变量。我们需要利用训练数据训练出模型,预测测试数据的目标变量。
评价指标
最终的评价指标为均方误差MSE,即:
S
c
o
r
e
=
1
n
∑
1
n
(
y
i
−
y
∗
)
2
Score = \frac{1}{n} \sum_1 ^n (y_i - y ^*)^2
Score=n11∑n(yi−y∗)2
2.代码实现
2.1 数据加载
data_train = pd.read_csv('../data/train.txt', sep='\t')
data_test = pd.read_csv('../data/test.txt', sep='\t')
print('训练集数据维度:',data_train.shape)
print('测试集维度',data_test.shape)
# 合并训练数据和测试数据
data_train["oringin"] = "train"
data_test["oringin"] = "test"
data_all = pd.concat([data_train, data_test], axis=0, ignore_index=True)
# 显示前5条数据
print(data_all.head())
结果打印:
训练集数据维度: (2888, 39)
测试集维度 (1925, 38)
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 4813 entries, 0 to 4812
Data columns (total 40 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V0 4813 non-null float64
1 V1 4813 non-null float64
2 V2 4813 non-null float64
3 V3 4813 non-null float64
4 V4 4813 non-null float64
5 V5 4813 non-null float64
6 V6 4813 non-null float64
7 V7 4813 non-null float64
8 V8 4813 non-null float64
9 V9 4813 non-null float64
10 V10 4813 non-null float64
11 V11 4813 non-null float64
12 V12 4813 non-null float64
13 V13 4813 non-null float64
14 V14 4813 non-null float64
15 V15 4813 non-null float64
16 V16 4813 non-null float64
17 V17 4813 non-null float64
18 V18 4813 non-null float64
19 V19 4813 non-null float64
20 V20 4813 non-null float64
21 V21 4813 non-null float64
22 V22 4813 non-null float64
23 V23 4813 non-null float64
24 V24 4813 non-null float64
25 V25 4813 non-null float64
26 V26 4813 non-null float64
27 V27 4813 non-null float64
28 V28 4813 non-null float64
29 V29 4813 non-null float64
30 V30 4813 non-null float64
31 V31 4813 non-null float64
32 V32 4813 non-null float64
33 V33 4813 non-null float64
34 V34 4813 non-null float64
35 V35 4813 non-null float64
36 V36 4813 non-null float64
37 V37 4813 non-null float64
38 target 2888 non-null float64
39 oringin 4813 non-null object
dtypes: float64(39), object(1)
通过观察数据,发现数据没有缺失值,所以不需要进行缺失值的补全
2.2 特征工程
2.2.1 核密度估计
**核密度估计(kernel density estimation)**是在概率论中用来估计未知的密度函数,属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。因为是传感器的数据,即连续变量,所以使用 kdeplot(核密度估计图) 进行数据的初步分析,即EDA。
for column in data_all.columns[0:-2]:
#核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数,属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。
g = sns.kdeplot(data_all[column][(data_all["oringin"] == "train")], color="Red", shade = True)
g = sns.kdeplot(data_all[column][(data_all["oringin"] == "test")], ax=g,color="Blue", shade= True)
g.set_xlabel(column)
g.set_ylabel("Frequency")
g = g.legend(["train","test"])
plt.show()
从画出的图中可以看出特征"V5",“V9”,“V11”,“V17”,“V22”,"V28"中训练集数据分布和测试集数据分布不均,所以我们删除这些特征数据。





2.2.2 特征之间的相关度
data_train1=data_all[data_all["oringin"]=="train"].drop("oringin",axis=1)
plt.figure(figsize=(20, 16)) # 指定绘图对象宽度和高度
colnm = data_train1.columns.tolist() # 列表头
mcorr = data_train1[colnm].corr(method="spearman") # 相关系数矩阵,即给出了任意两个变量之间的相关系数
mask = np.zeros_like(mcorr, dtype=np.bool) # 构造与mcorr同维数矩阵 为bool型
mask[np.triu_indices_from(mask)] = True # 角分线右侧为True
cmap = sns.diverging_palette(220, 10, as_cmap=True) # 返回matplotlib colormap对象,调色板
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f') # 热力图(看两两相似度)
plt.show()
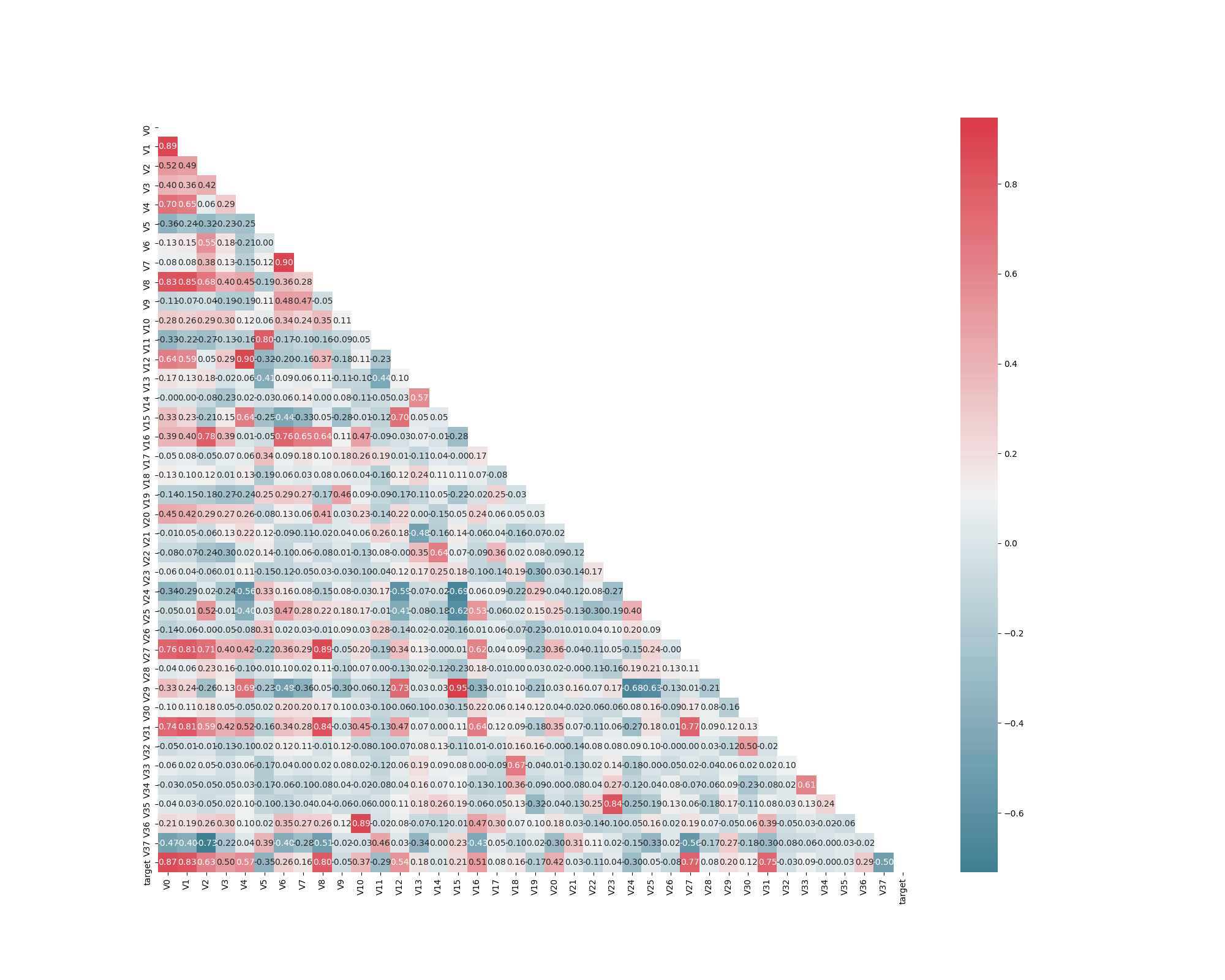
热力图在实际中常用于展示一组变量的相关系数矩阵,在展示列联表的数据分布上也有较大的用途,通过热力图我们可以非常直观地感受到数值大小的差异状况.热力图主要展示的是二维数据的数据关系。不同大小的值对应不同的颜色深浅,如上图,热力图的右侧是颜色带,上面代表了数值到颜色的映射,数值由小到大对应色彩由暗到亮。heatmap的API如下所示:
seaborn.heatmap(data, vmin=None, vmax=None, cmap=None, center=None, robust=False, annot=None, fmt='.2g', annot_kws=None, linewidths=0, linecolor='white', cbar=True, cbar_kws=None, cbar_ax=None, square=False, xticklabels='auto', yticklabels='auto', mask=None, ax=None, **kwargs)
vmax:设置颜色带的最大值
vmin:设置颜色带的最小值
cmap:设置颜色带的色系
center:设置颜色带的分界线
annot:是否显示数值注释
fmt:format的缩写,设置数值的格式化形式
linewidths:控制每个小方格之间的间距
linecolor:控制分割线的颜色
cbar_kws:关于颜色带的设置
mask:传入布尔型矩阵,若为矩阵内为True,则热力图相应的位置的数据将会被屏蔽掉(常用在绘制相关系数矩阵图)
自己算相关性系数矩阵的时候,代码中使用spearman系数,除此之外还有pearson、kendall两种系数,这三类相关系数是统计学上的三大重要相关系数,表示两个变量之间变化的趋势方向和趋势程度。现在简单介绍一下这三种相关系数:
-
Pearson 相关系数(连续变量)
假设条件:
a) 两个变量分别服从正态分布,通常用t检验检查相关系数的显著性;
b) 两个变量的标准差不为0。
结论:
pearson 描述的是线性相关关系,取值[-1, 1]。负数表示负相关,正数表示正相关。在显著性的前提下,绝对值越大,相关性越强。绝对值为0, 无线性关系;绝对值为1表示完全线性相关。
注:即使pearson相关系数为0,也只能说明变量之间不存在线性相关,但仍有可能存在曲线相关。
-
Spearman 秩相关系数(连续变量)
Spearman秩相关系数(斯皮尔曼等级相关)是一种非参数统计量,其值与两组相关变量的具体值无关,而仅仅与其值之间的大小关系有关。Spearman秩相关依据两列成对等级的各对等级数之差进行计算,所以又称为“等级差数法”。当变量在至少是有序的尺度上测量时,它是合适的相关分析方法。
Spearman秩相关同样应用于连续变量,与Pearson相关相比Spearman秩相关不要求变量的正态性和等方差假设,且对异常值的敏感度较低(该方法基于变量的排序,因此异常值的秩次通常不会有明显变化),因此适用范围通常更广。但方法较为保守,统计效能较Pearson相关系数低,容易忽略一些不太强的线性关系。
此外,Spearman秩相关要求数据必须至少是有序的,一个变量的得分必须与另一个变量单调相关(monotonically related)。
-
Kendall相关(分类变量,秩相关)
Kendall 相关系数则用于计算分类变量间的秩相关,用于反映分类变量相关性的指标,适用于两个分类变量均为有序分类的情况。
考虑两组变量,x和y,它们各自的观测值数量均为n,则x与y观测值可能配对的总数为n(n-1)/ 2。由于x和y为分类变量,需要首先根据类别表示的重要度人工赋值。随后考察x和y的关系对,如果xi<yi且xj<yj,或xi>yi且xj>yj,则该关系对是一致的(concordant),反正则不一致(discordant)。一致关系对数量与不一致关系对数量的差值除以总关系对数量,可得Kendall 相关系数。如果一致对的数量比不一致对的数量大得多,则变量是正相关的;如果一致对的数目比不一致对的数目少得多;则变量是负相关的;如果一致对的数目与不一致对的数目大致相同,则变量之间的关系很弱。
2.2.3 降维
进行降维操作,即将相关性的绝对值小于阈值的特征进行删除
threshold = 0.1
corr_matrix = data_train1.corr().abs()
drop_col=corr_matrix[corr_matrix["target"]<threshold].index
data_all.drop(drop_col,axis=1,inplace=True)
2.2.4 归一化
归一化:
1)把数据变成(0,1)或者(1,1)之间的小数。主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速。
2)把有量纲表达式变成无量纲表达式,便于不同单位或量级的指标能够进行比较和加权。归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。
具体代码如下
cols_numeric=list(data_all.columns)
cols_numeric.remove("oringin")
def scale_minmax(col):
return (col-col.min())/(col.max()-col.min())
scale_cols = [col for col in cols_numeric if col!='target']
data_all[scale_cols] = data_all[scale_cols].apply(scale_minmax,axis=0)
data_all[scale_cols].describe()
2.2.5 Box-Cox变换
Box 和 Cox在1964年提出的Box-Cox变换可使线性回归模型满足线性性、独立性、方差齐性以及正态性的同时,又不丢失信息。 Box-Cox变换是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。在做线性回归的过程中,不可观测的误差可能是和预测变量相关,于是给线性回归的最小二乘法估计系数的结果带来误差,为了解决这样的方差齐性问题,所以考虑对相应因变量做Box-Cox变换,变换之后,可以一定程度上减小不可观测的误差和预测变量的相关性,残差可以更好的满足正态性、独立性等假设前提,降低了伪回归的概率。但是选择的参数要适当,使用极大似然估计得到的参数,可以使上述过程的效果更好。当然,做过Box-Cox变换之后,方差齐性的问题不一定会消失,做过之后仍然需要做方差齐性的检验,看是否还需要采用其他方法。
除了Box-Cox变换,我们还可以使用一些普通的变换:

quantitle-quantile(q-q) plot(qq图):它主要是直观的表示观测与预测值之间的差异。一般我们所取得数量性状数据都为正态分布数据。预测的线是一条从原点出发的45度角的虚线,事假观测值是实心点。偏离线越大,则两个数据集来自具有不同分布的群体的结论的证据就越大。
用qq图画出转换前后数据的变化:
fcols = 6
frows = len(cols_numeric)-1
plt.figure(figsize=(4*fcols,4*frows))
i=0
for var in cols_numeric:
if var!='target':
dat = data_all[[var, 'target']].dropna()
i+=1
plt.subplot(frows,fcols,i)
sns.distplot(dat[var] , fit=stats.norm);
plt.title(var+' Original')
plt.xlabel('')
i+=1
plt.subplot(frows,fcols,i)
_=stats.probplot(dat[var], plot=plt)
plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
plt.xlabel('')
plt.ylabel('')
i+=1
plt.subplot(frows,fcols,i)
plt.plot(dat[var], dat['target'],'.',alpha=0.5)
plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))
i+=1
plt.subplot(frows,fcols,i)
trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
trans_var = scale_minmax(trans_var)
sns.distplot(trans_var , fit=stats.norm);
plt.title(var+' Tramsformed')
plt.xlabel('')
i+=1
plt.subplot(frows,fcols,i)
_=stats.probplot(trans_var, plot=plt)
plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
plt.xlabel('')
plt.ylabel('')
i+=1
plt.subplot(frows,fcols,i)
plt.plot(trans_var, dat['target'],'.',alpha=0.5)
plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))
plt.savefig('qq.png')
现展示部分特征的qq图,通过图像可知,通过Box-Cox转换后数据确实更接近于正态分布,测试集和训练集的分布更接近一致

2.2.6 对数变换
对数变换是数据变换的一种常用方式,之所以这样做是基于对数函数在其定义域内是单调增函数,取对数后不会改变数据的相对关系,取对数作用主要有:
**1. 缩小数据的绝对数值,方便计算。**例如,每个数据项的值都很大,许多这样的值进行计算可能对超过常用数据类型的取值范围,这时取对数,就把数值缩小了,例如TF-IDF计算时,由于在大规模语料库中,很多词的频率是非常大的数字。
2. 取对数后,可以将乘法计算转换称加法计算。
**3. 某些情况下,在数据的整个值域中的在不同区间的差异带来的影响不同。**对数值小的部分差异的敏感程度比数值大的部分的差异敏感程度更高
4. 取对数之后不会改变数据的性质和相关关系,但压缩了变量的尺度,例如800/200=4, 但log800/log200=1.2616,数据更加平稳,也消弱了模型的共线性、异方差性等。
5. 所得到的数据易消除异方差问题。
使用对数变换target目标值提升特征数据的正态性,代码如下:
sp = data_train.target
data_train.target1 =np.power(1.5,sp)
print(data_train.target1.describe())
数据转换前:

转换后:

2.3 模型构建
2.3.1 构造评价函数
from sklearn.metrics import make_scorer
# metric for evaluation
def rmse(y_true, y_pred):
diff = y_pred - y_true
sum_sq = sum(diff**2)
n = len(y_pred)
return np.sqrt(sum_sq/n)
def mse(y_ture,y_pred):
return mean_squared_error(y_ture,y_pred)
# scorer to be used in sklearn model fitting
rmse_scorer = make_scorer(rmse, greater_is_better=False)
#输入的score_func为记分函数时,该值为True(默认值);输入函数为损失函数时,该值为False
mse_scorer = make_scorer(mse, greater_is_better=False)
2.3.2 删除离群点
离群点检测(异常检测)是找出其行为不同于预期对象的过程,这种对象称为离群点或异常。离群点和噪声有区别,噪声是观测变量的随机误差和方差,而离群点的产生机制和其他数据的产生机制就有根本的区别。
全局离群点:通过找到某种合适的偏离度量方式,将离群点检测划为不同的类别;全局离群点是情景离群点的特例,因为考虑整个数据集为一个情境。
情境离群点:又称为条件离群点,即在特定条件下它可能是离群点,但是在其他条件下可能又是合理的点。比如夏天的28℃和冬天的28℃等。
集体离群点:个体数据可能不是离群点,但是这些对象作为整体显著偏移整个数据集就成为了集体离群点。
# function to detect outliers based on the predictions of a model
def find_outliers(model, X, y, sigma=3):
# predict y values using model
model.fit(X,y)
y_pred = pd.Series(model.predict(X), index=y.index)
# calculate residuals between the model prediction and true y values
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
# calculate z statistic, define outliers to be where |z|>sigma
z = (resid - mean_resid)/std_resid
outliers = z[abs(z)>sigma].index
# print and plot the results
print('R2=',model.score(X,y))
print('rmse=',rmse(y, y_pred))
print("mse=",mean_squared_error(y,y_pred))
print('---------------------------------------')
print('mean of residuals:',mean_resid)
print('std of residuals:',std_resid)
print('---------------------------------------')
print(len(outliers),'outliers:')
print(outliers.tolist())
plt.figure(figsize=(15,5))
ax_131 = plt.subplot(1,3,1)
plt.plot(y,y_pred,'.')
plt.plot(y.loc[outliers],y_pred.loc[outliers],'ro')
plt.legend(['Accepted','Outlier'])
plt.xlabel('y')
plt.ylabel('y_pred');
ax_132=plt.subplot(1,3,2)
plt.plot(y,y-y_pred,'.')
plt.plot(y.loc[outliers],y.loc[outliers]-y_pred.loc[outliers],'ro')
plt.legend(['Accepted','Outlier'])
plt.xlabel('y')
plt.ylabel('y - y_pred');
ax_133=plt.subplot(1,3,3)
z.plot.hist(bins=50,ax=ax_133)
z.loc[outliers].plot.hist(color='r',bins=50,ax=ax_133)
plt.legend(['Accepted','Outlier'])
plt.xlabel('z')
return outliers
2.3.3 模型训练
def train_model(model, param_grid=[], X=[], y=[],
splits=5, repeats=5):
# 获取数据
if len(y)==0:
X,y = get_trainning_data_omitoutliers()
# 交叉验证
rkfold = RepeatedKFold(n_splits=splits, n_repeats=repeats)
# 网格搜索最佳参数
if len(param_grid)>0:
gsearch = GridSearchCV(model, param_grid, cv=rkfold,
scoring="neg_mean_squared_error",
verbose=1, return_train_score=True)
# 训练
gsearch.fit(X,y)
# 最好的模型
model = gsearch.best_estimator_
best_idx = gsearch.best_index_
# 获取交叉验证评价指标
grid_results = pd.DataFrame(gsearch.cv_results_)
cv_mean = abs(grid_results.loc[best_idx,'mean_test_score'])
cv_std = grid_results.loc[best_idx,'std_test_score']
# 没有网格搜索
else:
grid_results = []
cv_results = cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=rkfold)
cv_mean = abs(np.mean(cv_results))
cv_std = np.std(cv_results)
# 合并数据
cv_score = pd.Series({'mean':cv_mean,'std':cv_std})
# 预测
y_pred = model.predict(X)
# 模型性能的统计数据
print('----------------------')
print(model)
print('----------------------')
print('score=',model.score(X,y))
print('rmse=',rmse(y, y_pred))
print('mse=',mse(y, y_pred))
print('cross_val: mean=',cv_mean,', std=',cv_std)
# 残差分析与可视化
y_pred = pd.Series(y_pred,index=y.index)
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
z = (resid - mean_resid)/std_resid
n_outliers = sum(abs(z)>3)
outliers = z[abs(z)>3].index
return model, cv_score, grid_results
-')
print('score=',model.score(X,y))
print('rmse=',rmse(y, y_pred))
print('mse=',mse(y, y_pred))
print('cross_val: mean=',cv_mean,', std=',cv_std)
# 残差分析与可视化
y_pred = pd.Series(y_pred,index=y.index)
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
z = (resid - mean_resid)/std_resid
n_outliers = sum(abs(z)>3)
outliers = z[abs(z)>3].index
return model, cv_score, grid_results
























 702
702

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








