集成学习之Stacking

最新推荐文章于 2025-03-21 15:10:27 发布

青转紫的梅子酒

最新推荐文章于 2025-03-21 15:10:27 发布

阅读量1.2w

点赞数 19

分类专栏：集成学习

本文链接：https://blog.csdn.net/u012867518/article/details/116748955

版权

集成学习专栏收录该内容

13 篇文章

订阅专栏

1. 基本概念

模型堆叠是一种数据科学基础方法，它依赖于多个模型的结果，即将多个弱学习器的结果进行组织，往往胜过单一的强模型。过去几年中大多数主要 kaggle 比赛的获胜者在最终获奖模型中都使用了模型堆叠。

堆叠模型类比于现实世界的例子，就比如商业团队，科学实验，或者体育团队。如果团队中的所有成员都非常擅长完成同样的任务，那么团队就会摧毁任何需要这个任务的挑战。

Stacking有“堆叠”的意思。从字面意思理解，Stacking方法就是将多个模型（同一层），进行多层堆砌（多层），然后得出最终的预测结果。可以将Stacking方法理解成并联 + 串联的关系。具体的集成方法如下图：

如上图，Stacking方法大致可以描述为：

将整个数据集Data分成训练集（TrainData）和测试集（TestData）。然后进行后续步骤：

Stage1：一层训练 - 以LR、SVM、GBDT、决策树、RF等5种算法为基础
1. 将训练集分为5折（TrainData_i, i=1,2,3,4,5） (仅以5折为例，也可以10折或者其他数量)。使用其中4折作为训练集（PartTrainData_i, i=1,2,3,4,5），1折作为验证集（ValiData_i, i=1,2,3,4,5）。
2. 使用 PartTrainData_i 训练出模型 Model_i（i=1,2,3,4,5），用 Model_i 预测 ValiData_i ，得到一个1折一维预测序列 ValiPredict_i（i=1,2,3,4,5）；同时，使用 Model_i 预测测试集 TestData ，也会得到一个一维预测序列 TestPredict_i 。如此循环，直到遍历完所有的组合。最终得到5个 ValiPredict_i 和5个 TestPredict_i ，将5个 ValiPredict_i 列向合并成一个一维预测序列 NewTrainData_ j （长度与 TrainData 长度一致）,同时对5个 TestPredict_i 求平均得到一个基于测试集的预测序列 NewTestData_ j （长度与 TestData 长度一致）。
3. 采用不同的算法（上例中是5种）重复1、2操作，最终得到5个 NewTrainData_ j 和5个 NewTestData_ j ，将5个 NewTrainData_ j 和5个 NewTestData_ j 分别进行行向合并，得到一个新的5维训练数据集 NewTrainData （加上Y后是6维）和一个新的5维测试数据集 NewTestData （加上Y后是6维）。
Stage2：二层训练 - 以XGBoost（或者LightGBM）算法为基础
1. 使用 Stage1 得到的新训练数据集 NewTrainData 和新测试数据集 NewTestData ，进一步训练得出一个XGBoost（或者LightGBM）模型，得到最终的预测分数。这种方法可以避免过拟合，学习出特征之间组合的信息，还能提高预测的准确率。

举个例子

首先将所有数据集生成测试集和训练集（假如训练集为10000,测试集为2500行），那么上层会进行5折交叉检验，使用训练集中的8000条作为训练集，剩余2000行作为验证集（橙色）。
每次验证相当于使用了绿色的8000条数据训练出一个模型，使用模型对验证集进行验证得到2000条数据，并对测试集进行预测，得到2500条数据，这样经过5次交叉检验，可以得到中间的5* 2000条验证集的结果(相当于每条数据的预测结果)，5* 2500条测试集的预测结果。
接下来会将验证集的5* 2000条预测结果拼接成10000行长的矩阵，标记为NewTrainData_1，而对于5* 2500行的测试集的预测结果进行加权平均，得到一个2500一列的矩阵，标记为TestPredict_1。
上一步得到一个基模型在数据集上的预测结果NewTrainData_1、TestPredict_1,这样当我们对5个基模型进行集成的话，相于得到了NewTrainData_1、NewTrainData_2、、NewTrainData3、NewTrainData_4、NewTrainData_5、TestPredict_1、TestPredict_2、TestPredict_3、TestPredict_4、TestPredict_5 十个矩阵。
之后我们会将NewTrainData_j并列在一起成10000行5列的矩阵作为training data,TestPredict_j合并在一起成2500行5列的矩阵作为testing data，让下层学习器基于这样的数据进行再训练。
再训练是基于每个基础模型的预测结果作为特征（五个特征），次学习器会进行学习训练。如果往这样的基学习的预测结果上赋予权重w，来使得最后的预测最为准确。

2.模型选择

通常情况下，Stacking 中第一层的模型会使用拟合度高的模型，以追求对训练数据的充分学习（如XGBoost、神经网络、SVM 等）。由于不同的模型在原理上和训练集上有所差别，第一层模型可以认为是从原始数据中自动提取有效特征的过程。第一层模型中，由于使用了复杂的非线性变化提取特征，Stacking 更易产生过拟合的情况。为了降低过拟合的风险，第二层模型倾向于使用简单的模型，例如逻辑回归、Lasso 回归等广义线性模型。从以上分析可以看出，Stacking 能够成功的关键在于第一层模型能针对原始训练数据得出有差异性（相关性低）且预测能力好的输出值，这样通过第二层模型进一步学习后，能够在多个第一层模型中取长补短，提升预测的准确度和稳定性。在传统的stacking集成学习中，第一层都使用相同的训练集数据，它们从不同的角度对相同的训练数据进行学习，得到具有差异性的输出值，再通过第二层的逻辑回归得到输出值。该框架主要应用于一些训练和预测数据同分布的传统领域，如图像分类。

3. Stacking与Blending

优点在于：

blending比stacking简单，因为不用进行k次的交叉验证来获得stacker feature
blending避开了一个信息泄露问题：generlizers和stacker使用了不一样的数据集

缺点在于：

blending使用了很少的数据（第二阶段的blender只使用training set 10%的量）
blender可能会过拟合
stacking使用多次的交叉验证会比较稳健

4. Stacking 与 bagging 和 boosting

Stacking 与 bagging 和 boosting 主要存在两方面的差异。首先，Stacking 通常考虑的是异质弱学习器（不同的学习算法被组合在一起），而bagging 和 boosting 主要考虑的是同质弱学习器。其次，stacking 学习用元模型组合基础模型，而bagging 和 boosting 则根据确定性算法组合弱学习器。

5. 代码实践

首先说一下我们今天要使用的库是mlxtend，在sklearn库中暂时还没有支持Stacking算法的类，所以在今天的例子中sklearn只能用来打辅助啦。mlxtend库是第三方库，可以通过pip install mlxtend直接安装即可。mlxtend兼容sklearn，可以组合sklearn生成的模型生成新的模型。我们今天使用的数据集是sklearn中的鸢尾花数据。

在mlxtend库中，如果实现分类算法，我们可以使用StackingClassifier或StackingCVClassifier，如果实现回归算法可以使用StackingRegressor或StackingCVRegressor，分类算法使用的两个类均为不使用交叉验证的Stacking算法，回归算法使用的两个类均为使用交叉验证的Stacking算法，大家可以根据需要选择。这里我们使用StackingCVClassifier，它主要有以下参数：

（1）classifiers：选择基分类器，以列表的形式传入初级学习器使用的模型，每个基分类器的属性可以查看类属性self._clfs_；
（2）meta_classifier：确定目标分类器；
（3）use_probas：默认为False，当设置为True时，目标分类器的输入就是前面分类输出的类别概率值；
（4）average_probas：上一个参数当使用概率值输出的时候是否使用平均值，默认为False；
（5）verbose：控制使用过程中的日志输出，当verbose为0时不输出，verbose取1时输出回归器的序号和名字，verbose取2时输出详细的参数信息，verbose大于2时自动将verbose设置为小于2的值，默认为0；
（6）use_features_in_secondary：默认为False，当设置为True时，最终的目标分类器就由基分类器产生的数据和最初的数据集同时训练，若设置为False，最终的分类器只使用基分类器产生的数据训练；
（7）cv：设定交叉验证折数

程序依赖包：

from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
import numpy as np
import warnings
warnings.simplefilter('ignore')
RANDOM_SEED = 42

5.1 简单堆叠CV分类

iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], #第一层分类器
                            meta_classifier=lr, #第二层分类器
                            random_state=RANDOM_SEED)

print('3-fold cross validation:\n')

for clf, label in zip([clf1, clf2, clf3, sclf], 
                      ['KNN', 
                       'Random Forest', 
                       'Naive Bayes',
                       'StackingClassifier']):

    scores = model_selection.cross_val_score(clf, X, y, 
                                              cv=3, scoring='accuracy')
    print("Accuracy: %0.2f (+/- %0.2f) [%s]" 
          % (scores.mean(), scores.std(), label))

结果输出：

3-fold cross validation:

Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.93 (+/- 0.02) [StackingClassifier]

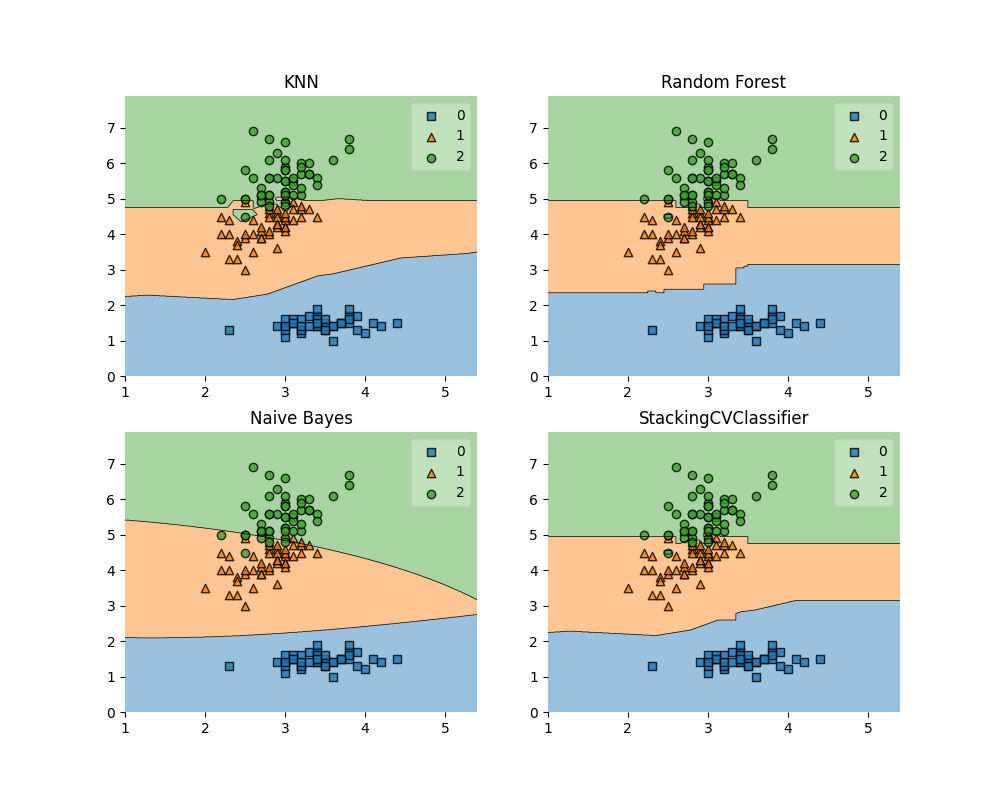
画出决策边界

import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertools

gs = gridspec.GridSpec(2, 2)
fig = plt.figure(figsize=(10,8))
for clf, lab, grd in zip([clf1, clf2, clf3, sclf], 
                         ['KNN', 
                          'Random Forest', 
                          'Naive Bayes',
                          'StackingCVClassifier'],
                          itertools.product([0, 1], repeat=2)):

    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf)
    plt.title(lab)
plt.show()

5.2 使用概率作为元特征

使用第一层所有基分类器所产生的类别概率值作为meta-classfier的输入。需要在StackingClassifier 中增加一个参数设置：use_probas = True。例如，在具有2个1级分类器的3级设置中，这些分类器可以为1个训练样本做出以下“概率”预测：

分类器1：[0.2、0.5、0.3]
分类器2：[0.3、0.4、0.4]

通过堆叠以下1级概率，得出k个特征，其中k = [n_classes * n_classifiers]：

[0.2、0.5、0.3、0.3、0.4、0.4]

另外，还有一个参数设置average_probas = True,那么这些基分类器所产出的概率值将按照列被平均，否则会拼接。

例如：

基分类器1：predictions=[0.2,0.2,0.7]

基分类器2：predictions=[0.4,0.3,0.8]

基分类器3：predictions=[0.1,0.4,0.6]

1）若use_probas = True，average_probas = True，

则产生的meta-feature 为：[0.233, 0.3, 0.7]

2）若use_probas = True，average_probas = False，

则产生的meta-feature 为：[0.2,0.2,0.7,0.4,0.3,0.8,0.1,0.4,0.6]

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
                            use_probas=True,
                            meta_classifier=lr,
                            random_state=42)

print('3-fold cross validation:\n')
for clf, label in zip([clf1, clf2, clf3, sclf], 
                      ['KNN', 
                       'Random Forest', 
                       'Naive Bayes',
                       'StackingClassifier']):

    scores = model_selection.cross_val_score(clf, X, y, cv=3, scoring='accuracy')
    print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))

输出结果：

3-fold cross validation:

Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [StackingClassifier]

5.3 堆叠的CV分类和GridSearch

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB 
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingCVClassifier

# Initializing models

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], 
                            meta_classifier=lr,
                            random_state=42)

params = {'kneighborsclassifier__n_neighbors': [1, 5],
          'randomforestclassifier__n_estimators': [10, 50],
          'meta_classifier__C': [0.1, 10.0]}

grid = GridSearchCV(estimator=sclf, 
                    param_grid=params, 
                    cv=5,
                    refit=True)
grid.fit(X, y)

cv_keys = ('mean_test_score', 'std_test_score', 'params')

for r, _ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r"
          % (grid.cv_results_[cv_keys[0]][r],
             grid.cv_results_[cv_keys[1]][r] / 2.0,
             grid.cv_results_[cv_keys[2]][r]))

print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)

输出

0.947 +/- 0.03 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.933 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Best parameters: {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
Accuracy: 0.95

如果我们计划多次使用回归算法，我们要做的就是在参数网格中添加一个附加的数字后缀，如下所示：

0.940 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.940 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.960 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.960 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Best parameters: {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
Accuracy: 0.96

注意：

该StackingClassifier还能够通过网格搜索classifiers参数。当存在级别混合的超参数时，GridSearchCV将尝试以自上而下的顺序替换超参数，即分类器->单基分类器->分类器超参数。例如，给定一个超参数网格，例如

params = {'randomforestclassifier__n_estimators': [1, 100],
'classifiers': [(clf1, clf1, clf1), (clf2, clf3)]}

它将首先使用（clf1，clf1，clf1）或（clf2，clf3）的实例设置。然后它将替换'n_estimators'基于的匹配分类器的设置'randomforestclassifier__n_estimators': [1, 100]。

5.4 在不同特征子集上运行的分类器的堆叠

不同的1级分类器可以适合训练数据集中的不同特征子集。以下示例说明了如何使用scikit-learn管道和ColumnSelector：


from sklearn.datasets import load_iris
from mlxtend.classifier import StackingCVClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression

iris = load_iris()
X = iris.data
y = iris.target

pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)),  # 选择第0,2列
                      LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)),  # 选择第1,2,3列
                      LogisticRegression())

sclf = StackingCVClassifier(classifiers=[pipe1, pipe2], 
                            meta_classifier=LogisticRegression(),
                            random_state=42)

sclf.fit(X, y)

输出：

StackingCVClassifier(classifiers=[Pipeline(steps=[('columnselector',
                                                   ColumnSelector(cols=(0, 2))),
                                                  ('logisticregression',
                                                   LogisticRegression())]),
                                  Pipeline(steps=[('columnselector',
                                                   ColumnSelector(cols=(1, 2,
                                                                        3))),
                                                  ('logisticregression',
                                                   LogisticRegression())])],
                     meta_classifier=LogisticRegression(), random_state=42)

5.5 ROC曲线与decision_function

像其他scikit-learn分类器一样，它StackingCVClassifier具有decision_function可用于绘制ROC曲线的方法。请注意，decision_function期望并要求元分类器实现decision_function。

from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
from sklearn.metrics import roc_curve, auc
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier


iris = datasets.load_iris()
X, y = iris.data[:, [0, 1]], iris.target


# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]



RANDOM_SEED = 42


X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=RANDOM_SEED)

clf1 =  LogisticRegression()
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = SVC(random_state=RANDOM_SEED)
lr = LogisticRegression()


sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
                            meta_classifier=lr)


# Learn to predict each class against the other
classifier = OneVsRestClassifier(sclf)

使用 predict_proba()

y_score = classifier.fit(X_train, y_train).predict_proba(X_test)

# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

png

使用 decision_function()

y_score = classifier.fit(X_train, y_train).decision_function(X_test)

# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

png

参考文档：

http://rasbt.github.io/mlxtend/user_guide/classifier/StackingCVClassifier/#example-4-stacking-of-classifiers-that-operate-on-different-feature-subsets