前几天有小伙伴问到这个算法,于是想总结一下好了,毕竟是一个如此著名的算法,这里就重在思想啦~建议配合实际例子学习。
参考:1)周志华:《机器学习》; 2)http://www.cnblogs.com/zhangchaoyang 作者:Orisun
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。其是一种监管学习,所谓监管学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。以二分类任务为例,决策树算法希望从给定训练数据集学得一个模型,用以对新的示例进行分类,可以看作是“当前样本属于正样本吗”问题的“决策”过程。
决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
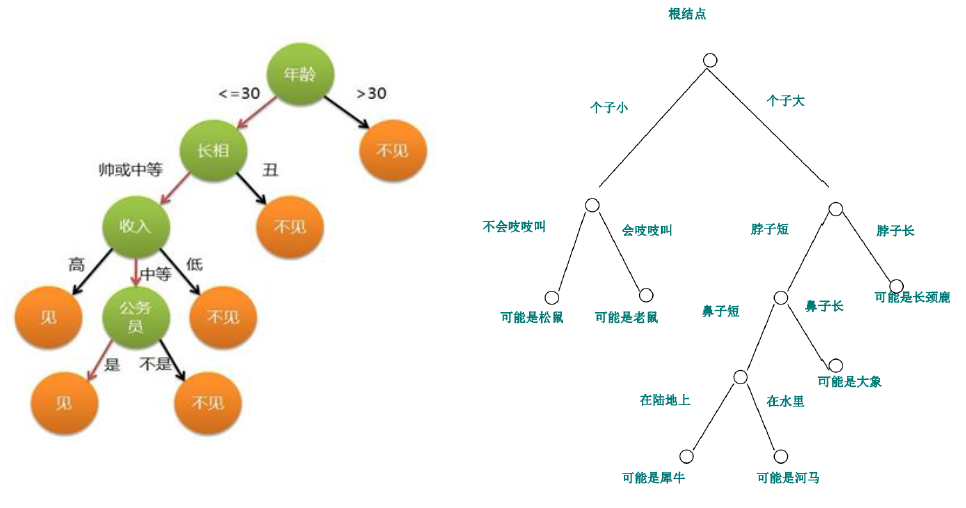
在网上找到的以下决策树示意图中,我来假设决策树的背景环境,左边图通过某一类人相亲结果大数据下的评价,完成该决策树,以便对以后该类同学的相亲时候进行初步预测来节约时间;右边图通过大量这几类动物特征数据完成,以便以后机器对一张图片一个视频里动物的快速分析。
为了通过大量数据,完成一个类似上图的决策树,就通过决策树算法实现。比较著名的决策树算法有ID3,C4.5,CART决策树等,其中,ICDM于2006年底评选数据挖掘十大经典算法,C4.5(分类决策树)居首,在这里讲一下C4.5决策树算法的主要思想。
决策树算法需要解决的两个主要问题:
1)先选择哪个属性,后选择哪个属性来进行分裂?2)什么时候树停止生长?
这里,C4.5算法是这样解决的:
1)用信息增益率来选择属性分裂;2)构造树的过程中进行剪枝操作降低过拟合风险。下面分别介绍。
1. 划分选择
即选择最优划分属性,一般对着划分过程的不断进行,即希望决策树的分支节点所包含的样本尽可能属于同一类,即节点的“纯度”越来越高。
这里引出“信息熵”的概念。“熵”是对混乱程度的度量,越乱熵越大,是一个度量样本集合纯度最常用的指标。划分节点处到底用哪个属性的时候,希望节点处属性纯度大,也就是熵更小。信息熵的计算公式如下:
用划分前(父节点)的不纯度和划分后(子女节点)的不纯度的差来来衡量属性分裂的测试结果,该指标成为信息增益,也就是熵的差,计算公式如下:
一般而言,信息增益越来,意味着用该属性进行划分所获得的“纯度提升”越大,因此可以作为划分属性的选择。ID3决策树即采用信息增益为准则选择划分属性。
但是实际上,信息增益对可取值数目较多的属性有所偏好,为减少这种不利,C4.5决策树算法产生,其将信息增益替换成增益率,来选择最优划分属性,其公式如下:
2.剪枝处理
剪枝处理通过主动去掉一些分支来降低决策树分支太多,来防止训练样本学习地太好(过拟合,把训练集自身的一些特点当做所有数据都具有的一般特性)的发生。在C4.5算法中,采用了悲观剪枝(PEP算法)的方法,使用训练集生成决策树,又用训练集来进行剪枝。
悲观剪枝主要通过递归估算每个内部节点所覆盖样本节点的误判率,然后假设需要进行剪枝操作,则剪枝后该内部节点会变成一个叶子节点,该叶子节点的类别为原内部节点的最优叶子节点所决定。计算比较剪枝前后该节点的错误率来决定是否进行剪枝。








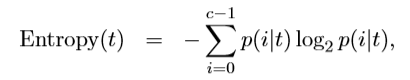
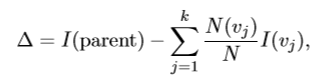
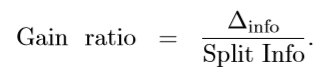
















 11万+
11万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








