5.1监督学习 239
5.1.1最近邻 241
5.1.2贝叶斯分类 243
5.1.3逻辑回归 248
5.1.4支持向量机 250
5.1.5决策树和森林 254
5.2无监督学习 257
5.2.1聚类 257
5.2.2K均值和高斯混合模型 259
5.2.3主成分分析 262
5.2.4流形学习 265
5.2.5半监督学习 266
5.3深度神经网络 268
5.3.1重量和层数 270
5.3.2激活函数 272
5.3.3正则化和归一化 274
5.3.4损失函数 280
5.3.5 Backpropagation 284
5.3.6培训和优化 287
5.4卷积神经网络 291
5.4.1池化和解池化 295
5.4.2应用:数字分类 298
5.4.3网络架构 299
5.4.4模型动物园 304
5.4.5可视化权重和激活 307
5.4.6对抗性示例 311
5.4.7自监督学习 312
5.5更复杂的模型 317
5.5.1三维CNN 317
5.5.2循环神经网络 321
5.5.3变压器 322
5.5.4生成模型 328
5.6其他阅读材料 336
5.7练习 337

图5.1机器学习与深度神经网络:(a)最近邻分类©Glassner(2018);(b)高斯核支持向量机(Bishop 2006)©2006斯普林格;(c)一个简单的三层网络©Glassner(2018);(d)SuperVision深度神经网络,由Matt Deitke提供(Krizhevsky、Sutskever和Hinton 2012);(e)网络准确率与规模及操作次数的关系(Canziani、Culurciello和Paszke 2017)©2017 IEEE;(f)网络特征可视化(Zeiler和Fergus 2014)©2014斯普林格。
机器学习技术在计算机视觉算法的发展中一直扮演着重要且往往是核心的角色。20世纪70年代,计算机视觉起源于人工智能、数字图像处理和模式识别(现称为机器学习)领域,我们领域的顶级期刊之一(《IEEE模式分析与机器智能汇刊》)至今仍保留着这一传统的印记。
图像处理、散点数据插值、变分能量最小化以及图形模型技术,在过去五十年中一直是计算机视觉中的重要工具。尽管机器学习和模式识别的元素也被广泛使用,例如用于微调算法参数,但它们真正崭露头角是在大规模标注图像数据集可用的情况下,如ImageNet (Deng,Dong等,2009;Russakovsky,Deng等,2015)、COCO (Lin,Maire等,2014)和LVIS (Gupta,Doll r,和Girshick,2019)。目前,深度神经网络是计算机视觉中最受欢迎和广泛使用的机器学习模型,不仅用于语义分类和分割,甚至用于低级任务,如图像增强、运动估计和深度恢复(Bengio
,LeCun,和Hinton,2021)。
图5.2展示了传统计算机视觉技术、机器学习算法和深度网络之间的主要区别。传统计算机视觉技术的所有处理阶段都是手工设计的;机器学习算法则将手工设计的特征传递给机器学习阶段;而深度网络则是直接从训练数据中学习所有算法组件,包括中间表示。
我们以经典机器学习方法的概述开始本章,如最近邻、逻辑回归、支持向量机和决策森林。这是一个广泛而深入的主题,我们仅简要总结主要流行的方法。关于这些技术的更多细节可以在相关教科书中找到,包括Bishop(2006)、Hastie、Tibshirani和Friedman(2009)、Murphy(2012)、Criminisi和Shotton(2013)以及Deisenroth、Faisal和Ong(2020)的著作。
本章的机器学习部分主要集中在分类任务中的监督学习上,在这种情况下,我们得到一组输入{xi },这些输入可能是从输入图像中提取的特征,并且与相应的类别标签(或目标){ti}配对,这些标签来自一组类别{Ck }。大多数用于监督分类的技术可以轻松扩展到回归,即将输入{xi }与实数值标量或向量输出{yi }关联起来,这在第4.1节中已经讨论过。我们还探讨了一些无监督学习的例子(第5.2节),在这种情况下没有标签或输出,以及半监督学习,其中仅提供样本子集的标签或目标。

图5.2传统、机器学习和深度学习管道,受古德-福尔德、本吉奥和库维尔(2016,图1.5)启发。在经典的视觉管道中,如结构从运动中提取特征,特征和算法都是传统上手工设计的(尽管可以使用学习技术,例如设计更可重复的特征)。经典机器学习方法采用提取的特征,利用机器学习构建分类器。深度学习管道则从像素开始到输出,通过端到端训练(由向后的虚线箭头表示)微调模型参数,从而学习整个管道。
本章的后半部分重点讨论深度神经网络,这些网络在过去十年中已成为大多数计算机视觉识别和低级视觉任务的首选方法。我们首先介绍构成深度神经网络的基本元素,包括权重和激活函数、正则化项以及使用反向传播和随机梯度下降进行训练的方法。接下来,我们将介绍卷积层,回顾一些经典架构,并讨论如何预训练网络及其性能可视化。最后,我们简要提及更高级的网络,如三维和时空模型,以及递归和生成对抗网络。
因为机器学习和深度学习是如此丰富而深入的主题,本章仅简要总结了一些主要概念和技术。关于经典机器学习的综合著作包括Bishop(2006)、Hastie、Tibshirani和Friedman(2009)、Murphy(2012)以及Deisenroth、Faisal和Ong(2020),而专注于深度学习的教科书则包括Goodfellow、Bengio和Courville(2016)、Glassner(2018)、Glassner(2021),

图5.3在监督学习中,使用配对的训练输入和标签来估计能够最好地预测标签的模型参数。运行时,模型参数(通常)被冻结,然后将模型应用于新输入以生成所需的输出。©张,Lipton et al(2021,图1.3)
以及Zhang、Lipton等人(2021)。
机器学习算法通常被分类为监督型或非监督型,其中监督型是将配对的输入和输出提供给学习算法(图5.3),而非监督型是提供统计样本而没有相应的标记输出(第5.2节)。
如图5.3所示,监督学习涉及将输入对{xi }及其对应的输出值{ti }输入到学习算法中,该算法调整模型参数,以最大化模型预测与目标输出之间的吻合度。输出可以是来自类别集合{Ck }的离散标签,也可以是一组连续的、可能为向量值的数值,我们用yi来区分这两种情况。第一种任务称为分类,因为我们试图预测类别归属;而第二种任务称为回归,因为历史上,根据数据拟合趋势被称为回归(第4.1节)。

经过训练阶段,在此期间所有训练数据(标记的输入-输出对)都已处理完毕(通常通过多次迭代完成),训练好的模型现在可以用于预测以前未见过的输入的新输出值。这一阶段常被称为测试阶段,尽管这有时会误导人们过分关注特定测试集上的表现,而不是构建一个能够稳健应对可能出现的任何合理输入的系统。
在本节中,我们更多地关注分类问题,因为我们已经在前一章讨论了一些更简单的(线性和核)回归方法。计算机视觉中最常见的分类应用之一是语义图像分类,即我们希望为整个图像(或预设部分)标注其最可能的语义类别,例如马、猫或汽车(第6.2节)。这是深度网络(第5.3-5.4节)最初开发的主要应用。然而,近年来,这些网络也被应用于连续像素标注任务,如语义分割、图像去噪以及深度和运动估计。更复杂的任务,如目标检测和实例分割,将在第6章中介绍。
在我们开始回顾传统的监督学习技术之前,应该更正式地定义一下系统试图学习的内容,即“最大化模型预测与目标输出之间的一致性”是什么意思。最终,就像任何其他计算机算法一样,在不确定、嘈杂和/或不完整的数据下偶尔会出错,我们也希望最大化其预期效用,或者相反,最小化其预期损失或风险。这是决策理论的主题,相关内容在机器学习教科书中有所详细解释(Bishop 2006,第1.5节;Hastie、Tibshirani和Friedman 2009,第2.4节;Murphy 2012,第6.5节;Deisenroth、Faisal和Ong 2020,第8.2节)。
我们通常无法获得输入的真实概率分布,更不用说输入与相应输出的联合分布了。因此,我们经常使用训练数据分布作为现实世界分布的代理。这种近似被称为经验风险最小化(参见上述关于决策理论的引用),其中预期风险可以通过以下方式估计:
(5.1)
损失函数L衡量的是在输入xi和模型参数w对应的目标值yi时,预测输出f(xi;w)的“成本”。
这个公式现在应该相当熟悉了,因为它与我们在前一章(4.2;4.15)中介绍的回归公式相同。在那些情况下,成本(惩罚)是目标输出yi和模型f(xi;w)预测输出之间的差异的简单二次或稳健函数。在某些情况下,我们可能希望损失函数能够模拟特定的预测不对称性。例如,在自主导航中,通常高估最近障碍物的距离,可能导致碰撞,其代价比保守地低估要大得多。我们将看到更多关于损失函数的例子。
本章后面部分,包括第5.1.3节关于贝叶斯分类(5.19–5.24)和第5.3.4节关于神经网络损失(5.54–5.56)。
在分类任务中,通常会尽量减少误分类率,即使用一个与类别无关的delta函数来等量惩罚所有类预测错误(Bishop2006,第1.5.1–1.5.2节)。然而,不对称性常常存在。例如,在医学领域,产生假阴性诊断的成本往往高于假阳性诊断的成本,后者可能需要进一步检查。我们将在第7.1.3节中更详细地讨论真阳性和假阳性、阴性以及错误率。
数据预处理
在我们开始回顾广泛使用的机器学习技术之前,应该提到通常最好对输入数据进行中心化、标准化处理,如果可能的话,还要白化(Glassner2018,第10.5节;Bishop2006,第12.1.3节)。特征向量的中心化意味着减去它们的均值,而标准化则意味着重新缩放每个分量,使其方差(与均值的平方距离的平均值)为1。
美白是一个计算成本较高的过程,涉及计算输入的协方差矩阵,取其奇异值分解,然后旋转坐标系,使最终维度不相关且具有单位方差(在高斯模型下)。虽然这可能对低维输入非常实用和有帮助,但对于大量图像集来说,可能会变得极其昂贵。(但请参见第5.2.3节关于主成分分析的讨论,在该部分中,它可能是可行且有用的。)
有了这个背景,我们现在把注意力转向一些广泛使用的监督学习技术,即最近邻、贝叶斯分类、逻辑回归、支持向量机和决策树和森林。
最近邻是一种非常简单的非参数技术,即不涉及底层分布的低参数解析形式。相反,所有训练样本都被保留,在评估时找到“最近”的k个邻居,然后取平均值以生成输出。3
图5.4显示了k的各种值的简单图形示例,即使用
从k = 1最近邻一直到找到k = 25最近邻并选择

图5.4最近邻分类。为了确定星(★)测试样本的类别,我们找到k个最近邻并选择最流行的类别。此图显示了k = 1、9和25个样本的结果。©Glassner(2018)

图5.5对于噪声(混合)数据,选择过小的k值会导致不规则的决策面。选择过大的k值可能导致小区域缩小或消失。©Glassner(2018)
将计数最高的类别作为输出标签。如您所见,改变邻居的数量会影响最终的类别标签,从红色变为蓝色。
图5.5展示了以另一种方式改变邻居数量的效果。图的左半部分显示了初始样本,这些样本分为蓝色或橙色两类。可以看出,训练样本高度混合,即没有明确(合理的)边界能够正确地标记所有样本。图的右侧显示了当k值从1到50变化时,k-NN分类器的决策边界。当k太小时,分类器的行为非常随机,即过度拟合训练数据(第4.1.2节)。随着k值增大,分类器欠拟合(过度平滑)数据,导致两个较小区域的收缩。选择最佳最近邻数量k是该算法的一个超参数。确定合适值的技术包括交叉验证,我们在第4.1.2节中讨论过。
虽然最近邻是一种相当粗暴的机器学习技术(尽管
科弗和哈特(1967)证明,在大样本极限下,这种方法在统计上是最优的),但在许多计算机视觉应用中仍然有用,例如大规模匹配和索引(第7.1.4节)。然而,随着样本数量的增加,必须使用高效技术来找到(精确或近似)最近邻。在通用计算机科学和更专业的计算机视觉领域,已经开发出了寻找最近邻的良好算法。
穆贾和洛(2014)开发了一个快速近邻库(FLANN),该库汇集了多个先前开发的算法,并被纳入OpenCV。该库实现了几种强大的近邻算法,包括随机k-树(西尔帕-阿南和哈特利2008年)、优先搜索k均值树、近邻算法(弗里德曼、本特利和芬克尔1977年)以及局部敏感哈希(LSH)(安多尼和因迪克2006年)。他们的库可以根据数据索引的特性,实证确定使用哪种算法及其参数。
最近,Johnson、Douze和J gou(2021)开发
了支持GPU的Faiss库,用于扩展相似性搜索(第6.2.3节),支持数十亿个向量。该库基于乘积量化(J gou、Douze和Schmid 2010),作者证明其在Faiss库开发的大规模数据集上表现
优于LSH (Gordo、Perronnin等2013)。
对于一些简单的机器学习问题,例如,如果我们有一个特征构建和噪声的解析模型,或者我们可以收集足够的样本,我们就可以确定每个类别的特征向量的概率分布p(xjCk)以及先验类别似然p(Ck)。根据贝叶斯规则(4.33),给定特征向量x(图5.6)时,类别Ck的似然值由下式给出:

图5.6一个例子,展示了两个类条件密度p(儿|Ck)以及相应的后验类别概率p(Ck|儿),这些可以通过贝叶斯规则获得,即通过除以两条曲线的总和(Bishop 2006)©2006斯普林格。垂直的绿色线是用于最小化误分类率的最佳决策边界。
其中,第二种形式(使用exp函数)被称为归一化指数或softmax函数。6该量
lk = log p(xjCk)+ log p(Ck) (5.4)
是样本x属于类别Ck的对数似然。有时,将softmax函数(5.3)表示为一个向量到向量的值函数是方便的,
p = softmax(l)。 (5.5)
软最大值函数可以看作是最大指示函数的软版本,当lk的最大值主导其他值时,它返回1。它在机器学习和统计学中被广泛使用,包括作为深度神经分类网络中的最终非线性函数(图5.27)。
使用公式(5.2)确定给定特征向量x的类Ck的可能性的过程被称为贝叶斯分类,因为它结合了条件特征似然p(xjCk)和类别p(Ck)的先验分布,使用贝叶斯规则来确定
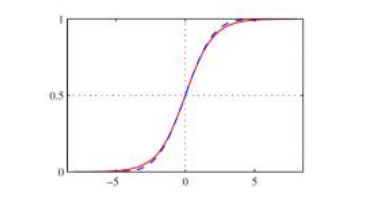
图5.7红色显示的逻辑S型函数σ(l),以及虚线蓝色显示的缩放误差函数(Bishop2006)©2006 Springer。
后验类概率。在特征向量的分量是独立生成的情况下,即,
(5.6)
由此产生的技术被称为nave Bayes分类器。
对于二元(两类)分类任务,我们可以将(5.3)重写为
(5.7)
其中,l = l0 - l1是两个类别的对数似然的差异,被称为对数几率或logit。
σ(l)函数被称为逻辑S型函数(或简称逻辑函数或逻辑曲线),其中S型表示S形曲线(图5.7)。S型函数曾是早期神经网络中常用的激活函数,尽管现在已被其他函数所取代,具体讨论见第5.3.2节。
线性和二次判别分析
虽然基于归一化指数和sigmoid的概率生成分类可以应用于任何一组对数似然,但当分布是多维高斯时,公式变得简单得多。
对于具有相同协方差矩阵Σ的高斯分布,我们有

图5.8两个相同分布的高斯类别的逻辑回归(Bishop 2006)©2006斯普林格出版社:(a)红色和蓝色表示两个高斯分布;(b)后验概率p(C0 jx),以函数的高度和红色墨水的比例表示。
在两类(二分类)的情况下,我们得到(Bishop2006,第4.2.1节)
p (C0 jx) = σ(wTx + b), (5.9)
和
(5.11)
方程(5.9)在非生成性(判别性)分类(5.18)的背景下,我们将在稍后重新讨论,被称为逻辑回归,因为我们传递线性回归公式的输出
l (x) = wTx + b (5.12)
通过逻辑函数获得一个类别概率。图5.8在二维中说明了这一点,右侧显示红色类别的后验似然p(C0 jx)。
在线性回归(5.12)中,w起到权重向量的作用,我们沿着这个向量投影特征向量x,而b则充当偏置,决定了分类边界的设置位置。请注意,权重方向(5.10)与连接分布均值的向量(通过逆协方差Σ-1旋转坐标后)一致,而偏置项则与均值平方矩和对数类别先验比值log(p(C0)/p(C1))成正比。

图5.9二次判别分析(Bishop2006)©2006 Springer。当类协方差Σk不同,高斯分布之间的决策面变为二次面。
对于K > 2类,可以将softmax函数(5.3)应用于线性回归对数似然函数,
lk (x) = wx + bk , (5.13)
和
wk = Σ-1μk,以及 (5.14)
(5.15)
因为分类从一个类别转换到另一个类别的决策边界是线性的,
wk x + bk > wl x + bl , (5.16)
使用此类标准对示例进行分类的技术称为线性判别分析(Bishop2006,第4.1节;Murphy2012,第4.2.2节)。8
到目前为止,我们已经研究了所有类别协方差矩阵Σk都相同的案例。当它们在不同类别之间变化时,决策面不再是线性的,而是变得二次(图5.9)。这些二次决策面的推导被称为二次判别分析(Murphy2012,第4.2.1节)。
在高斯类分布不可用的情况下,我们仍然可以使用Fisher判别分析(Bishop2006,第4.1.4节;Murphy2012,第8.6.3节)找到最佳判别方向,如图5.10所示。这种分析在单独使用时非常有用。

图5.10 Fisher线性判别(Bishop2006)©2006 Springer。为了找到最佳分离两个类别的投影方向,我们计算两个类别协方差的总和,然后使用其逆矩阵来旋转两个类别均值之间的向量。
对不同类别内的变异性进行建模,例如不同人的外观变化(第5.2.3节)。
在上一节中,我们基于应用于多元高斯分布的后验概率推导了分类规则。然而,高斯分布通常不是我们类分布的合适模型,我们必须采用其他技术。
其中最简单的是逻辑回归,它应用了与前一节相同的想法,即线性投影到权重向量上,
li = w · xi + b (5.17)
pi = p(C0 jxi)= σ(li)= σ(wT xi + b) (5.18)
获取(二进制)类别概率。逻辑回归是判别模型的一个简单例子,因为它不构建或假设未知数的先验分布,因此不是生成性的,即我们无法从类别中生成随机样本(Bishop2006,第1.5.4节)。
由于我们不再有类平均值和协方差的分析估计(或者它们是类分布的劣质模型),我们需要其他方法来确定权重w和偏置b。我们通过最大化正确标签的后验对数似然函数来实现这一点。
对于二分类任务,令ti∈{0,1}为每个训练样本xi的类别标签,pi = p(C0 jx)为给定条件下由(5.18)预测的似然估计值。
权重和偏置(w,b)。我们可以通过最小化负对数似然,即交叉熵损失或误差函数,来最大化正确标签被预测的可能性
(Bishop2006,第4.3.2节)。9注意,每当标签ti = 0时,我们希望pi = p(C0 jxi)值较高,反之亦然。
这个公式可以很容易地扩展到多类损失,再次定义后验概率为每个类别的线性回归的归一化指数,如(5.3)和(5.13),
(5.20)
lik = wxi + bk . (5.21)
术语Zi = Σj exp lij可以作为推导中的一个有用的简写,有时也被称为分区函数。经过一些操作(Bishop2006,第4.3.4节),相应的多类交叉熵损失(a.k.a.多项式逻辑回归目标)变为
(5.22)
其中,1-of-K(或otherwise
).10)更常见的是简单地使用整数类值ti作为目标,在这种情况下,我们可以更简洁地重写它为
(5.23)
即,我们只是将每个训练样本的正确类别的对数似然相加。将softmax公式(5.20)代入这个损失函数,我们可以将其重写为
为了确定最佳权重和偏置集{wk;bk },我们可以使用梯度下降法,即使用牛顿-拉夫森二阶优化方案(Bishop 2006,第4.3.3节)更新它们的值,
w ← w - H-1▽E(w); (5.25)
其中,▽E是损失函数E关于权重变量w的梯度,H是E的二阶导数的海森矩阵。由于交叉熵函数在未知权重上不是线性的,我们需要多次迭代求解这个方程以获得一个好的解。因为H中的元素在每次迭代后都会更新,这种方法也被称为迭代重加权最小二乘法,我们将在第8.1.4节中详细讨论。虽然许多非线性优化问题存在多个局部最小值,但本节描述的交叉熵函数没有,因此我们可以保证找到唯一的解。
逻辑回归确实存在一些局限性,因此通常仅用于最简单的分类任务。如果特征空间中的类别不是线性可分的,使用简单的投影到权重向量上可能无法生成足够的决策面。在这种情况下,核方法(第4.1.1节和5.1.4节;Bishop 2006,第6章;Murphy 2012,第14章)可以测量新(测试)特征向量与选择的训练样本之间的距离,通常能提供良好的解决方案。
逻辑回归的另一个问题是,如果类别实际上是可分离的(无论是原始特征空间还是提升核空间),则可能存在多个独特的分离平面,如图5.11a所示。此外,除非进行正则化,否则权重w将继续增大,因为较大的wk值会导致较大的pik值(一旦找到分离平面),从而导致总体损失减小。
出于这个原因,我们讨论了将决策面以最大化其与标记示例的分离的方式放置的技术。
正如我们刚才提到的,在某些逻辑回归的应用中,我们无法确定一个单一的最佳决策面(即权重和偏置向量{wk;bk }在公式(5.21)中的选择),因为特征空间中存在多个平面可以引入。请参见图5.11a,其中两个类别分别用青色和洋红色表示。除了两条虚线和一条实线外,还有无数条其他直线也能干净地分离这两个类别,包括一系列水平线。由于这些直线中的任何一条的分类错误都是零,那么如何选择最佳决策面呢?考虑到我们只有有限数量的训练样本,以及实际运行时的例子

图5.11 (a)支持向量机(SVM)找到最大化与最近训练样本距离的线性决策面(超平面),这些训练样本被称为支持向量©Glassner(2018)。(b)一个二维二分类的例子,高斯核支持向量机(Bishop2006)©2006斯普林格。红色和蓝色的×表示训练样本,绿色圈出的样本是支持向量。黑色线条表示核回归函数的等值线,其中包含蓝色和红色支持向量的等值线表示士1等值线,中间的深色等值线则是决策面。
可能介于两者之间?
这个问题的答案是使用最大间隔分类器(Bishop2006,第7.1节),如图5.11a所示,虚线表示两个具有最大间隔的平行决策面,即它们之间的最大垂直距离。实线代表位于虚线之间等距的超平面,这就是最大间隔分类器。
为什么这是一个好主意?有几个潜在的推导(Bishop2006,第7.1节),但一个相当直观的解释是,可能存在我们尚未见过的青色和品红色类别的实际例子。在某些假设下,最大间隔分类器为我们提供了正确分类尽可能多这些未见过的例子的最佳选择。
为了确定最大间隔分类器,我们需要找到一个权重-偏置对(w;b),使得所有回归值li = w·xi + b(5.17)的绝对值至少为1,并且符号正确。为了更简洁地表示这一点,设
i = 2ti—1;i∈{—1;1} (5.26)
i (w · xi + b) ≥ 1. (5.27)
为了最大化利润,我们只需找到满足(5.27)的最小范数权重向量w,即求解优化问题
arg min ⅡwⅡ2 (5.28)
w;b
受(5.27)约束。这是一个典型的二次规划问题,可以使用拉格朗日乘数法求解,如Bishop (2006,第7.1节)所述。
不等式约束恰好满足,即它们在图5.11a中的两条虚线处变为等式,其中我们有li = wxi +b =士1。触碰虚线的圆圈点称为支持向量。对于一个简单的线性分类器,可以用单个权重和偏置对(w,b)表示,计算支持向量实际上没有实际优势,除了它们有助于我们估计决策面。然而,正如我们将要看到的,当我们应用核回归时,拥有少量的支持向量是一个巨大的优势。
如果两个类无法线性分离,实际上需要一个复杂的曲面才能正确分类样本,如图5.11b所示,该怎么办?在这种情况下,我们可以用核回归(4.3)替代线性回归,这在第4.1.1节中已经介绍过。我们不再将权重向量w与特征向量x相乘,而是将其与以数据点位置xk为中心的K个核函数值相乘,
(5.29)
这就是支持向量机真正发挥作用的地方。
不再需要对所有训练样本xk进行求和,一旦我们解决了最大间隔分类器的问题,只需保留一小部分支持向量,如图5.11b中圈出的十字所示。从图中可以看出,用深黑色线表示的决策边界很好地分离了红色和蓝色类别的样本。请注意,与其他核回归应用一样,径向基函数的宽度仍然是一个自由的超参数,必须合理调整以避免欠拟合和过拟合。

图5.12用于重叠类别分布的支持向量机(Bishop2006)©2006斯普林格。(a)绿色圈出的点位于y = 1决策边界错误一侧,其惩罚值为ξ = 1—y > 0。(b)支持向量机中使用的“铰链”损失以蓝色显示,同时以红色显示的是重新缩放的逻辑回归损失函数,黑色表示误分类误差,绿色表示平方误差。
铰链损失。到目前为止,我们关注的是可分离的分类问题,即存在一个决策边界能够正确分类所有训练样本。支持向量机也可以应用于重叠(混合)类别分布(图5.12a),而之前我们是通过逻辑回归来处理这类问题的。在这种情况下,我们将不等式条件(5.27),即ili≥1,替换为铰链损失惩罚。
EHL(li,i)= [1—ili]+,[1—ili]+, (5.30)
其中[·]+表示正部分,即[x]+ = max(0,x)。图5.12b中以蓝色显示的铰链损失惩罚,在满足(先前)不等式时为0,并且根据不等式的违反程度线性增加。为了找到最优权重值(w,b),我们最小化正则化的铰链损失值之和,
图5.12b将铰链损失与公式(5.19)中的逻辑回归(交叉熵)损失进行了比较。铰链损失不对位于j lij > 1边界正确一侧的训练样本施加惩罚,而交叉熵损失则倾向于较大的绝对值。虽然在本节中我们主要关注了支持向量机的二分类版本,但Bishop (2006,第7章)描述了多类扩展以及高效的优化算法,如顺序最小优化(SMO)(Platt 1989)。此外,还有一个很好的
scikit-learn网站上的在线教程。12 Lampert(2008)对应用于计算机视觉的SVM和其他核方法进行了调查。
与本章迄今为止我们研究的大多数监督学习技术不同,这些技术一次性处理完整的特征向量(通过线性投影或与训练样本的距离),决策树则执行一系列更简单的操作,通常只是查看单个特征元素,然后决定下一步查看哪个元素(Hastie,Tibshirani和Friedman 2009,第17章;Glassner 2018,第14.5节;Criminisi,Shotton和Konukoglu 2012;Criminisi和Shotton 2013)。(请注意,我们在第6.3.1节中讨论的提升方法也使用类似的简单决策树。)尽管决策树在统计机器学习中已使用了几十年(Breiman,Friedman等1984),但其更强大的扩展——决策森林的应用直到十多年前才开始在计算机视觉领域获得关注(Lepetit和Fua 2006;Shotton,Johnson和Cipolla 2008;Shotton,Girshick等2013)。与支持向量机一样,决策树是判别分类器(或回归器),因为它们从未明确形成所分类数据的概率(生成)模型。
图5.13展示了决策树和随机森林的基本概念。在这个例子中,训练样本来自四个不同的类别,每个类别用不同的颜色表示(a).决策树(b)从上到下构建,通过选择每个节点上的决策,将到达该节点的训练样本进一步细分为更具体的(低熵)分布。每条链接的粗细显示了沿此路径分类的样本数量,链接的颜色则是通过该链接流动的类别颜色的混合。颜色直方图显示了几个内部节点处的类别分布。
随机森林(c)是通过构建一系列决策树来创建的,每棵树做出的决策略有不同。在测试(分类)时,新的样本会被随机森林中的每棵树分类,最终在叶子节点处的类别分布会被平均,从而提供比单个树(给定深度)更准确的答案。
随机森林有多个设计参数,可以用来调整其准确性、泛化能力以及运行时间和空间复杂度。这些参数包括:
每棵树的深度D,

图5.13决策树和森林(Criminisi和Shotton 2013)©2013斯普林格。左上角的(a)图显示了一组训练样本标签,用四种不同的颜色表示。右上角的(b)显示了一个单个决策树,在每个节点处都有一个类别的分布(根节点的分布与整个训练集相同)。在测试(c)时,每个新示例(特征向量)都会在根节点处进行测试,根据测试结果(例如,某个元素与阈值的比较),决定是否向下走至其子节点。这一过程会一直持续到达到具有特定类别分布的叶节点。在训练(b)时,选择的决策能够减少节点子节点处的熵(提高类别特异性)。底部的(c)图显示了三棵树的集成。当每个树对特定测试示例进行了分类后,所有组成树的叶节点的类别分布会被平均。

图5.14随机森林决策面(Criminisi和Shotton 2013)©2013斯普林格。图(a)和(b)显示了使用ρ = 500和ρ = 5随机假设在每个分裂节点获得的T = 400树森林之间的“噪声”量较小和较大。在每张图中,两行分别展示了不同深度(D = 5和13)的树,而列则显示了使用轴对齐或线性决策面(“弱学习器”)的效果。
ρ.节点构建时检查的样本数量。
仅通过查看所有训练示例的随机子集ρ,每个树最终在每个节点上都有不同的决策函数,因此可以对树的集合进行平均以产生更软的决策边界。
图5.14展示了这些参数对一个简单的四类二维螺旋数据集的影响。在这个图中,树的数量固定为T = 400。克里米尼西和肖顿(2013年,第4章)提供了更多参数变化效果的额外图表。该图的左半部分(a)和右半部分(b)分别显示了决策节点处随机性减少(ρ = 500)和增加(ρ = 5)的效果。较少的随机性会产生更清晰的决策面,但可能泛化能力较差。在每个2×2的图像网格中,上排显示的是较浅的D = 5树,而下排显示的是更深的D = 13树,这使得决策边界中的细节更加精细。(与所有机器学习一样,训练数据上的更好性能并不一定意味着更好的泛化能力,因为可能会出现过拟合。)最后,右列显示了如果轴向(单元素)决策被特征元素的线性组合所替代会发生什么。
当应用于计算机视觉时,决策树首先在关键点识别(Lepetit和Fua 2006)和图像分割(Shotton、Johnson和Cipolla 2008)领域产生了影响。它们是人类姿态估计从Kinect深度图像中取得突破性成功的关键因素之一(Shotton、Girshick等2013)。此外,决策树还推动了最先进的医学图像分割系统的发展(Criminisi、Robertson等2013),尽管这些系统现在已被深度神经网络所取代(Kamnitsas、Ferrante等2016)。大多数这些应用,以及其他一些应用,在Criminisi和Shotton编辑的书中都有详细回顾(2013)。
到目前为止,在本章中,我们主要关注了监督学习技术,即给定包含输入和目标示例对的训练数据。然而,在某些应用中,我们只有一组数据,希望对其进行特征描述,例如,观察是否存在任何模式、规律或典型分布。这通常是经典统计学的研究领域。在机器学习界,这种情况通常被称为无监督学习,因为样本数据没有标签。计算机视觉中的应用实例包括图像分割(第7.5节)以及人脸和身体识别与重建(第13.6.2节)。
在本节中,我们将探讨计算机视觉中一些更广泛使用的技术,即聚类和混合模型(例如用于分割)以及主成分分析(用于外观和形状建模)。还有许多其他技术可供选择,这些内容可以在机器学习教科书中找到,如Bishop (2006,第9章)、Hastie、Tibshirani和Friedman (2009,第14章)以及Murphy (2012,第1.3节)。
你可以用样本数据做的最简单的事情之一就是根据相似性(例如向量距离)将其分组。在统计学中,这个问题被称为聚类分析,是一个广泛研究的领域,有数百种不同的算法(Jain和Dubes 1988;Kaufman和Rousseeuw 1990;Jain、Duin和Mao 2000;Jain、Topchy等2004)。Murphy (2012,第25章)对聚类算法进行了很好的阐述,包括亲和传播、谱聚类、图拉普拉斯、层次聚类、凝聚聚类和分裂聚类。Xu和Wunsch(2005)的综述更为全面,涵盖了近300篇不同论文,涉及相似度度量、向量量化、混合模型、核方法、组合和神经网络算法以及可视化等主题。图5.15显示了

图5.15使用简化版https://scikit-learn.org/stable/auto examples/cluster/ plot cluster comparison.html#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py.生成的一些玩具数据集上不同聚类算法的比较
将https://scikit-learn.org聚类分析包中实现的一些算法应用于一些简单的二维例子。
将图像分割成越来越细的区域(分割聚类)是计算机视觉中最古老的技术之一。奥兰德、普赖斯和雷迪(1978)提出了一种这样的技术,首先计算整个图像的直方图,然后找到最佳阈值以分离直方图中的大峰值。这一过程会重复进行,直到区域变得相对均匀或低于某个特定大小。更近期的分割算法通常优化某些区域内相似性和区域间差异性的度量。这些内容将在第7.5.3节和第4.3.2节中讨论。
区域合并技术也可以追溯到计算机视觉的初期。Brice和Fennema(1970)使用双网格来表示像素之间的边界并进行合并
根据相对边界长度和这些边界处可见边缘的强度来划分区域。
在数据聚类中,算法可以根据最接近点之间的距离(单链接聚类)、最远点之间的距离(完全链接聚类)或介于两者之间的距离(贾因、托普奇等人,2004年)将聚类连接起来。卡姆瓦尔、克莱因和曼宁(2002年)提供了这些算法的概率解释,并展示了如何在此框架内引入额外的模型。第7.5节讨论了此类凝聚聚类(区域合并)算法在图像分割中的应用。
均值移位(第7.5.2节)和模式查找技术,例如k均值和高斯混合,将与每个像素相关的特征向量(例如颜色和位置)建模为未知概率密度函数的样本,然后尝试在该分布中寻找聚类(模式)。
考虑图7.53a所示的彩色图像。仅凭颜色,你如何分割这幅图像?图7.53b展示了L*u*v*空间中的像素分布,这相当于忽略空间位置的视觉算法所看到的情况。为了简化可视化,我们只考虑L*u*坐标,如图7.53c所示。你看到了多少明显的(拉长的)聚类?你会如何找到这些聚类?
k-均值和高斯混合技术使用密度函数的参数模型来回答这个问题,即假设密度是由少量较简单的分布(例如高斯分布)叠加而成,这些分布的位置(中心)和形状(协方差)可以被估计。而均值漂移则平滑分布并找到其峰值以及每个峰值对应的特征空间区域。由于建模的是完整的密度,这种方法被称为非参数方法(Bishop2006)。
K-均值算法隐式地将概率密度建模为球对称分布的叠加,无需任何概率推理或建模(Bishop2006)。相反,该算法被赋予要找到的聚类数量k,并通过从输入特征向量中随机抽取k个中心点来初始化。然后,它根据最接近每个中心的样本迭代更新聚类中心的位置(图5.16)。此外,还开发了基于统计特性来分割或合并聚类中心的技术,以及加速寻找最近均值中心的过程(Bishop2006)。
在高斯混合模型中,每个聚类中心都通过一个协方差矩阵进行增强,该矩阵的值是从相应的样本中重新估计的(图5.17)。与使用近邻来关联输入样本和聚类中心不同,马氏距离(Ap-

图5.16 k均值算法从一组样本和所需聚类的数量开始(在这种情况下,k = 2)(Bishop2006)©2006 Springer。它迭代地将样本分配给最近的平均值,然后重新计算平均中心,直到收敛。

图5.17使用期望最大化(EM)的高斯混合模型(GMM)(Bishop2006)©2006 Springer。样本根据其马氏距离(逆协方差加权距离)被软性地分配到聚类中心,然后基于这些加权分配重新计算新的均值和协方差。
d(xi,μk;Σk)= Ⅱxi - μk ⅡΣk-1 =(xi - μk)T Σk-1(xi - μk) (5.32)
其中,xi是输入样本,μk是聚类中心,Σk是它们的协方差估计值。样本可以与最近的聚类中心相关联(一种硬分配成员身份),也可以软地分配给几个附近的聚类。
后一种更常用的方法对应于对高斯混合模型的参数进行迭代重新估计,
(5.33)
其中πk是混合系数,μk和Σk是高斯均值和协方差,以及
(5.34)
为正态(高斯)分布(Bishop2006)。
为了迭代计算未知混合参数{πk,μk,Σk }的(局部)最大似然估计,期望最大化(EM)算法(Shlezinger1968;Dempster,Laird,and Rubin1977)在两个交替阶段进行:
1.期望阶段(E步)估计责任
(5.35)是样本xi从第k个高斯聚类生成的可能性的估计值。
2.最大化阶段(M步)更新参数值
是分配给每个簇的样本点数的估计值。
Bishop(2006)对高斯混合估计和更一般的期望最大化主题进行了精彩的阐述。
在图像分割的背景下,Ma、Derksen等人(2007)对使用高斯混合进行分割进行了很好的回顾,并基于最小描述长度(MDL)编码开发了他们自己的扩展,他们表明这在Berkeley分割数据集上产生了良好的结果。
正如我们在混合分析中所看到的,用多元高斯模型对聚类中的样本进行建模是捕捉其分布的一种强有力的方法。不幸的是,随着我们样本空间的维度增加,估计完整的协方差很快变得不可行。
例如,考虑所有正面人脸的空间(Figure5.18)。对于由P个像素组成的图像,协方差矩阵的大小为P×P。幸运的是,完整的协方差通常不需要建模,因为可以使用主成分分析估计较低秩的近似值,如AppendixA.1.2所述。
PCA最初用于计算机视觉中,用于建模人脸,即特征脸,最初用于灰度图像(Kirby和Sirovich1990;Turk和Pentland1991),然后用于3D模型(Blanz和Vetter1999;Egger、Smith等人2020)(第13.6.2节)和主动外观模型(第6.2.4节),其中还用于建模面部形状变形(Rowland和Perrett1995;Cootes、Edwards和Taylor2001;Matthews、Xiao和Baker 2007)。
特征脸。特征脸依赖于Kirby和Sirovich(1990)首先观察到的,任意人脸图像x可以通过从平均图像m(Figure6.1b)开始,并添加少量缩放的带符号图像ui来压缩和重建,
(5.40)
签名基图像(图5.18b)可以通过主成分分析(也称为特征值分析或Karhunen—Love变换)从一组训练图像中得出。Turk和Pentland(1991)认识到,特征脸展开中的系数ai本身可以用来构建快速图像匹配算法。

图5.18使用特征脸进行面部建模和压缩(Moghaddam和Pentland 1997)©1997 IEEE: (a)输入图像;(b)前八个特征脸;(c)通过投影到该基底并压缩图像至85字节重建的图像;(d)使用JPEG (530字节)重建的图像。
更详细地说,我们从一组训练图像{xj }开始,从中计算平均图像m和一个散射或协方差矩阵
(5.41)
(5.42)
其中λi是C的特征值,ui是特征向量。对于一般图像,Kirby和Sirovich(1990)称这些向量为特征图像;对于人脸,Turk和Pentland(1991)称它们为特征脸(Figure5.18b).13
特征值分解的两个重要性质是,对于任何新的图像x,最优(最佳近似)系数ai可以计算为
ai = (x — m) · ui , (5.43)
并且,假设特征值{λi }按降序排列,在任何点M截断(5.40)给出的近似值,可以得到最佳的近似值(最小 x.图5.18c显示了与图5.18a对应的近似结果,并显示了它在压缩人脸
图像方面比JPEG好多少。
截断人脸图像的特征面分解(5.40)在M个分量之后,相当于将图像投影到一个线性子空间F上,我们可以称之为人脸空间

(Moghaddam和Pentland1997)©1997 IEEE。面部空间距离(DFFS)为
与平面的正交距离,而面空间中的距离(DIFS)是距离
从平均图像出发,沿着平面移动。这两个距离都可以转换成马氏距离,并给出概率解释。
(图5.19)。因为特征向量(特征面)是正交的,并且具有单位范数,所以
其中DIFS代表面部空间中的距离(Moghaddam和Pentland1997)。重新
面部空间距离(DFFS)可以直接在像素空间中计算,表示特定图像的“人脸性”。也可以通过取其特征人脸系数差的范数来测量两个不同面部在面部空间中的距离。
然而,在欧几里得向量空间中计算这些距离并没有充分利用协方差矩阵(5.42)的特征值分解所提供的额外信息。为了根据测量的协方差正确加权距离,我们可以使用马氏距离(5.32)(附录B.1)。类似地,可以对人脸空间(DFFS)(Moghaddam和Pentland 1997)进行合理的差异分析,并将这两个项结合起来,以估计是否为真实人脸的可能性,这在人脸识别中非常有用(第6.3.1节)。关于概率性和贝叶斯主成分分析的更详细解释可以在统计学习教科书中找到(Bishop 2006;Hastie,Tibshirani和Friedman 2009;Murphy 2012),这些书籍还讨论了选择用于建模分布的最佳组件数M的技术。
关于特征脸用于识别的最初研究(Turk和Pentland 1991)在Moghaddam和Pentland(1997)、Heisele、Ho等人(2003)以及Heisele、Serre和Poggio(2007)的工作中得到了扩展,包括模块化特征空间,用于分别建模不同面部组件如眼睛、鼻子和嘴巴的外观,以及基于视角的特征空间,用于分别建模不同视角下的面部。Belhumeur、Hespanha和Kriegman(1997)进一步扩展了这一工作,以处理因光照引起的外观变化,分别建模个人内部和外部的变异性,并使用Fisher线性判别分析(图5.10)进行识别。随后,Moghaddam、Jebara和Pentland(2000)开发了贝叶斯扩展。这些扩展在引用的论文以及本书第一版(Szeliski 2010,第14.2节)中有更详细的描述。
还可以将PCA和SVD方法中隐含的双线性分解推广到多线性(张量)公式,这些公式可以同时建模多个相互作用的因素(Vasilescu和Terzopoulos2007)。这些想法与机器学习中的其他主题有关,如子空间学习(Cai,He等人2007)、局部距离函数(Frome,Singer等人2007;Ramanan和Baker2009)以及度量学习(Kulis2013)。
在许多情况下,我们分析的数据并不位于全局线性子空间中,而是存在于低维流形上。在这种情况下,可以使用非线性降维方法(Lee和Verleysen 2007)。由于这些系统在高维空间中提取低维流形,因此也被称为流形学习技术(Zheng和Xue 2009)。图5.20显示了使用scikit-learn流形学习包从三维S形带状物中提取的一些二维流形示例。14
这些结果只是众多算法中的一小部分,其中包括多维缩放(Kruskal 1964a,b)、Isomap (Tenenbaum、De Silva和Langford 2000)、局部线性嵌入(Roweis和Saul 2000)、Hessian特征映射(Donoho和Grimes 2003)、拉普拉斯特征映射(Belkin和Niyogi 2003)、局部切空间对齐(Zhang和Zha 2004)、通过学习不变映射进行降维(Hadsell、Chopra和LeCun 2006)、改进的LLE(Zhang和Wang 2007)、t分布随机邻域嵌入(t-SNE)(van der Maaten和Hinton 2008;van der Maaten 2014)以及UMAP (McInnes、Healy和Melville 2018)。许多这些算法在Lee和Verleysen(2007)、Zheng和Xue(2009)以及文献中进行了综述。

图5.20曲面学习的例子,即非线性降维,应用于https://scikit-learn.org/stable/modules/ manifold.html中的1,000个点,每个点有10个邻居。八个样本输出由八种不同的嵌入算法生成,具体描述见scikit-learn曲面学习文档页面。
维基百科。15 Bengio,Paiement等人(2004)描述了一种扩展此类算法的方法,用于计算新(“样本外”)数据点的嵌入。McQueen,Meila等人(2016)描述了他们的megaman软件包,该软件包能够高效解决包含数百万数据点的嵌入问题。
除了降维可以用于数据正则化和加速相似性搜索外,流形学习算法还可以用于可视化输入数据分布或神经网络层激活。图5.21展示了将两种此类算法(UMAP和t-SNE)应用于三个不同的计算机视觉数据集的例子。
在许多机器学习场景中,我们拥有一小部分准确标注的数据和大量未标注或标注不准确的数据。例如,像ImageNet这样的图像分类数据集可能只包含一百万张标注图像,但网络上可找到的图像总数却要大几个数量级。我们能否利用这个更大的数据集,尽管它仍然捕捉到了我们预期未来输入的特征,来构建更好的分类器或预测器?

图5.21比较UMAP和t-SNE流形学习算法©McInnes、Healy和Melville(2018)在三个不同的计算机视觉学习识别任务上的表现:COIL (Nene、Nayar和Murase 1996)、MNIST (LeCun、Cortes和Burges 1998)以及Fashion MNIST (Xiao、Rasul和Vollgraf 2017)。

图5.22半监督学习的例子(Zhu和Goldberg2009)©2009 Morgan和Claypool:(a)两个标记样本和一个连接所有样本的图;(b)用谐波函数解决二元标记,解释为电阻电网络;
(c)使用半监督支持向量机(S3VM)。
考虑图5.22中的简单示意图。即使只有少量的例子被正确地标记了类别(在这种情况下,用红色和蓝色的圆圈或点表示),我们仍然可以想象将这些标签(归纳地)扩展到附近的样本,从而不仅标记所有数据,还能为未来的输入构建合适的决策面。
这一研究领域被称为半监督学习(Zhu和Goldberg 2009;Subra- manya和Talukdar 2014)。一般来说,它分为两种类型。在转导学习中,目标是同时对所有未标记的输入和已标记的例子进行分类,即图5.22中显示的所有点和圆圈。在归纳学习中,我们训练一个机器学习系统,该系统能够对未来的输入进行分类,即输入空间中的所有区域。后一种形式更为广泛使用,因为在实际应用中,大多数机器学习系统用于在线应用,如自动驾驶或新内容分类。
半监督学习是弱监督学习问题的一个子集,在这类问题中,训练数据不仅可能缺少标签,还可能存在准确性存疑的标签(Zhou2018)。计算机视觉领域的一些早期例子(Torresani 2014)包括利用互联网上的图像标签构建完整的图像分类器(Fergus,Perona和Zisserman 2004;Fergus,Weiss和Torralba 2009),以及在训练数据中存在缺失或非常粗糙的边界的情况下进行物体检测和/或分割(定位)(Nguyen,Torresani等2009;Deselaers,Alexe和Ferrari 2012)。在深度学习时代,弱监督学习仍然被广泛使用(Pathak,Krahenbuhl和Darrell 2015;Bilen和Vedaldi 2016;Arandjelovic,Gronat等2016;Khoreva,Benenson等2017;Novotny,Larlus和Vedaldi 2017;Zhai,Oliver等2019)。最近一个将弱监督学习应用于数十亿噪声标注图像的例子是在Instagram图片上带有话题标签的情况下预训练深度神经网络(Mahajan,Girshick等2018)。我们将在第5.4.7节中探讨用于预训练神经网络的弱监督和自监督学习技术。
正如我们在本章引言中所见(图5.2),深度学习管道采取了端到端的方法来处理机器学习,通过搜索能够最小化训练损失的参数来优化每个处理阶段。为了使这种搜索可行,如果损失是所有这些参数的可微函数会更有帮助。深度神经网络提供了一个统一且可微的计算架构,同时还能自动发现有用的内部表示。
人们对于构建模拟神经(生物)计算的计算系统很感兴趣
自20世纪50年代末以来,这一领域经历了起伏。当时,罗森布拉特(1958)提出了感知器,而威德罗和霍夫(1960)推导出了权重适应增量规则。到了20世纪70年代末,一群自称为连接主义者的研究人员重新激发了这些领域的研究热情,围绕这一主题组织了一系列会议,最终促成了1987年神经信息处理系统(NeurIPS)会议的成立。塞诺夫斯基(2018)最近的一本书对这一领域的发展进行了很好的历史回顾,古德费洛、本吉奥和库尔维尔(2016)以及张、利普顿等人(2021)的引言,拉瓦特和王(2017)的综述论文,以及本吉奥、勒昆和欣顿(2021)的图灵奖演讲,也都对此进行了探讨。尽管大多数深度学习社区已经远离了生物学上的合理模型,但仍有一些研究继续探索生物视觉系统与神经网络模型之间的联系(亚明斯和迪卡洛2016;庄、严等人2020)。
一个很好的论文集可以在麦克莱伦、鲁梅尔哈特和PDP研究小组(1987)中找到,其中包括关于反向传播的开创性论文(鲁梅尔哈特、欣顿和威廉姆斯1986a),该论文为现代前馈神经网络的训练奠定了基础。在那段时间以及随后的几十年里,开发了多种替代的神经网络架构,包括使用随机单元的架构,如玻尔兹曼机(阿克利、欣顿和塞若夫斯基1985)和受限玻尔兹曼机(欣顿和萨拉赫丁诺夫2006;萨拉赫丁诺夫和欣顿2009)。本吉奥(2009)的综述回顾了这些早期深度学习方法的一些情况。许多这些架构都是我们在第4.3节中看到的生成图形模型的例子。
当今最受欢迎的深度神经网络是具有实值激活函数的确定性判别前馈网络,采用梯度下降训练,即反向传播训练规则(Rumelhart,Hinton和Williams 1986b)。当与卷积网络的思想结合时(Fukushima 1980;LeCun,Bottou等1998),深度多层神经网络在语音识别(Hinton,Deng等2012)和视觉识别(Krizhevsky,Sutskever和Hinton 2012;Simonyan和Zisserman 2014b)领域取得了突破,这些成果出现在2010年代初。张、利普顿等人(2021,第7章)对这些突破的组成部分以及自那时以来深度网络的快速演变进行了很好的描述,早期的综述论文(Rawat和Wang 2017)也有类似的内容。
与其他机器学习技术相比,后者通常依赖多个预处理阶段来提取可用于构建分类器的特征,而深度学习方法通常是端到端训练的,直接从原始像素过渡到最终所需输出(无论是分类还是其他图像)。在接下来的几节中,我们将描述基本的

图5.23一个感知器单元(a)明确显示权重与输入相乘,(b)权重写在输入连接上,(c)最常见的形式,省略了权重和偏置。加权求和后跟随一个非线性激活函数。©Glassner(2018)
构建和训练此类神经网络所需的组件。关于每个主题的更详细解释可以在深度学习教科书中找到(Nielsen 2015;Goodfellow,Bengio和Courville 2016;Glassner 2018,2021;Zhang,Lipton等2021),以及Li、Johnson和Yeung(2019)和Johnson(2020)编写的优秀课程笔记中。
深度神经网络(DNN)是由数千个简单互连的“神经元”(单元)组成的前馈计算图,其输入的加权和与逻辑回归(5.18)类似
如果= wxi + bi (5.45)
yi = h(si), (5.46)
如图5.23所示。xi是第i个单元的输入,wi和bi是其可学习的权重和偏置,si是加权线性和的输出,yi是si通过激活函数h后的最终输出。16每个阶段的输出通常称为

激活信号随后被输入到后续阶段的单元中,如图Figure5.24.17所示
最早的此类单元被称为感知器(Rosenblatt1958),其图示如图5.23a所示。请注意,在这个最初的图中,权重在学习阶段(第5.3.5节)优化时被明确显示,并与逐元素乘法一起展示。图5.23b展示了一种形式,其中权重写在连接线(单元之间的箭头,尽管箭头通常被省略)之上。更常见的是将网络图示为图5.23c所示的形式,在这种形式中,权重(以及偏置)完全省略并假定存在。
神经网络通常被组织成连续的层,如图5.25所示,而不是像图5.24那样连接成一个不规则的计算图。现在我们可以将一层中的所有单元视为一个向量,相应的线性组合写为
sl = Wl xl ; (5.47)
其中xl是层l的输入,Wl是权重矩阵,sl是加权和,并且使用一组激活函数对加权和应用元素非线性,
xl+1 = yl = h (sl ). (5.48)
使用全(密集)权重矩阵进行线性组合的层称为全连接(FC)层,因为一个层的所有输入都连接到它的所有输入
请注意,尽管几乎所有前馈神经网络都使用输入的线性加权和,但新认知器(福岛1980)还包含了一个受生物神经元行为启发的除法归一化阶段。一些最新的深度神经网络也支持使用条件批量归一化(Section5.3.3)实现激活之间的乘法交互。

图5.25绘制神经网络的两种不同方法:(a)底部为输入,顶部为输出
顶部,左侧为(b)输入,右侧为输出。©Glassner(2018)
输出。正如我们将在第5.4节中看到的,当处理像素(或其他信号)时,早期处理阶段使用卷积而不是密集连接,以实现空间不变性和更高的效率。18仅由全连接层(不含卷积层)组成的网络现在通常被称为多层感知器(MLP)。
大多数早期神经网络(Rumelhart、Hinton和Williams 1986b;LeCun、Bottou等1998)使用了类似于逻辑回归中使用的S形函数。较新的网络,从Nair和Hinton(2010)以及Krizhevsky、Sutskever和Hinton(2012)开始,使用了修正线性单元(ReLU)或其变体。ReLU激活函数定义为
h (y) = max (0; y) (5.49)
如图5.26左上角所示,以及一些其他流行函数,它们的定义可以在各种出版物中找到(例如,Goodfellow,Bengio和Courville 2016,第6.3节;Clevert,Unterthiner和Hochreiter 2015;He,Zhang等人。

图5.26来自©Glassner(2018)的一些流行的非线性激活函数:从左上到右下:ReLU、leaky ReLU、shifted ReLU、maxout、softplus、ELU、sigmoid、tanh、swish。
不幸的是,ReLU单元在训练过程中可能很脆弱,并且可能会“死亡”。
例如,一个大的梯度流经ReLU神经元可能会导致权重更新,使得该神经元不再激活任何数据点。如果发生这种情况,那么从那时起,通过该单元的梯度将永远为零。也就是说,在训练过程中,ReLU单元可能会不可逆地死亡,因为它们可能被踢出数据流形。. ..通过适当设置学习率,这个问题发生的频率会降低。

图5.27 (a)用于从神经网络激活(“分数”)转换的softmax层
(b)顶部行显示激活,底部行显示通过softmax运行分数以获得适当归一化的似然的结果。©Glassner(2018)。
如果出现这个问题。
对于用于分类的网络的最后一层,通常使用softmax函数(5.3)将实值激活转换为类别概率,如图5.27所示。因此,我们可以认为倒数第二组神经元决定了激活空间中与相应类别的对数似然最接近的方向,同时最小化其他类别的对数似然。由于输入向前传递到最终输出的类别和概率,前馈网络是判别性的,即它们没有输出类别的统计模型,也没有直接从这些类别生成样本的方法(但参见第5.5.4节了解实现这些方法的技术)。
与其他形式的机器学习一样,正则化和其他技术可以用来防止神经网络过拟合,从而更好地泛化到未见过的数据。在本节中,我们将讨论可以应用于大多数机器学习系统的传统方法,如正则化和数据增强,以及特定于神经网络的技术,如丢弃和批量归一化。
正如我们在第4.1.1节中所见,对权重施加二次或p-范数惩罚(4.9)可以改善系统的条件性并减少过拟合。当p = 2时,会产生常规的L2正则化,使较大的权重变小;而使用p = 1则被称为

图5.28来自MNIST数据库的原始“6”位数字和两个弹性变形
版本(Simard、Steinkraus和Platt2003)©2003 IEEE。
拉索(最小绝对收缩和选择算子)可以将某些权重完全降至零。当神经网络内部优化权重时,这些项会使权重变小,因此这种正则化也被称为权重衰减(Bishop 2006,第3.1.4节;Goodfellow、Bengio和Courville 2016,第7.1节;Zhang、Lipton等2021,第4.5节)。需要注意的是,对于更复杂的优化算法如Adam,L2正则化和权重衰减并不等价,但可以通过修改算法恢复权重衰减的优良特性(Loshchilov和Hutter 2019)。
数据集增强
另一种强大的减少过拟合的技术是通过扰动已收集样本的输入和/或输出来增加更多的训练样本。这种技术被称为数据集增强(Zhang,Lipton等,2021年,第13.1节),在图像分类任务中尤为有效,因为获取标记示例的成本很高,而且图像类别在小范围局部扰动下不应发生变化。
早期应用于神经网络分类任务的一个例子是西马德、斯坦克劳斯和普拉特(2003)提出的弹性畸变技术。在他们的方法中,为每个训练样本生成随机的低频位移(扭曲)场,并在训练过程中应用于输入(图5.28)。请注意,这种畸变与简单地向输入添加像素噪声不同。相反,畸变会移动像素,从而在输入向量空间中引入更大的变化,同时仍然保留了示例的语义意义(在这种情况下,MNIST数字(勒昆、科尔特斯和伯吉斯1998))。

图5.29使用dropout时,在训练过程中,网络中的一部分单元p被移除(或者等效地,被限制为零)©Srivastava,Hinton (2014)。对每个小批量随机执行此操作,可将噪声注入到训练过程中(网络的所有级别),并防止网络过度依赖特定单元。
Dropout是由斯里瓦斯塔瓦、欣顿等人(2014)引入的一种正则化技术,在训练过程中,每个小批量中(第5.3.6节),每层的某个百分比p(例如50%)的单元会被固定为零,如图5.29所示。随机将单元设为零可以向训练过程注入噪声,同时防止网络过度针对特定样本或任务进行优化,这两点都有助于减少过拟合并提高泛化能力。
因为丢弃(归零)单位的p会减少该单位对任何总和贡献的期望值,减少比例为(1 - p),所以每一层中的加权总和si(5.45)在训练过程中会被乘以(1-p)^-1。测试时,网络运行时不进行丢弃也不对总和进行补偿。关于丢弃的更详细描述,可参见张、利普顿等人(2021年,第4.6节)和约翰逊(2020年,第10讲)。
优化深度神经网络中的权重是一个棘手的过程,可能收敛速度较慢。我们将在第5.3.6节中详细讨论这一过程。
迭代优化技术的一个经典问题是条件不良,其中梯度的分量在大小上变化很大。虽然有时
在采取步骤之前,可以通过预处理技术对单个元素进行梯度缩放(第5.3.6节和附录A.5.2)来减少这些影响,但通常最好是在问题制定过程中控制系统的条件数。
在深度网络中,条件不良的一种表现形式是连续层中的权重或激活值变得不平衡。假设我们取一个给定的网络,并将某一层数值为100×的所有权重放大,同时将下一层的权重缩小相同的比例。由于ReLU激活函数在其两个域内都是线性的,第二层的输出仍然相同,尽管第一层输出的激活值会大100倍。在梯度下降步骤中,经过这种重新缩放后,关于权重的导数将大不相同,实际上与权重本身大小相反,需要极小的梯度下降步长来防止过冲(见练习5.4)。22
批量归一化(Ioffe和Szegedy 2015)的核心思想是重新缩放(并重新中心化)给定单元的激活值,使其具有单位方差和零均值(对于ReLU激活函数而言,这意味着该单元在一半的时间内处于激活状态)。我们通过考虑给定小批量B中的所有训练样本n(5.71),计算单元i的均值和方差统计量来进行这种归一化。

其中s是训练样本n中单位i的加权和,i(n)是相应的批次
归一化总和,∈(通常为10-5)是一个小常数,用于防止除以零。
在批次归一化之后,i(n)激活现在具有零均值和单位方差。
然而,这种归一化可能与训练过程中最小化损失函数的目的相悖。因此,Ioffe和Szegedy(2015)为每个单元i添加了一个额外的增益γi和偏置βi参数,并定义批归一化阶段的输出为
22这段鼓舞人心的文字是我对为什么批量归一化可能是个好主意的个人解释,与批量归一化减少内部协变量偏移的观点有关,这一观点被(Ioffe和Szegedy 2015)用来为其技术辩护。这一假设现在正受到质疑,替代理论正在被开发(Bjorck、Gomes等2018;Santurkar、Tsipras等2018;Kohler、Daneshmand等2019)。
这些参数的作用就像常规权重一样,即在训练过程中使用梯度下降对其进行修改以减少总体训练损失。
批量归一化的一个细微之处在于,μi和σ的数量是分析性的
对于给定单元在小批量中的所有激活。为了正确定义梯度下降,损失函数关于这些变量的导数,以及量i和yi关于这些变量的导数,必须作为梯度计算步骤的一部分进行计算,使用类似于原始反向传播算法(5.65–5.68)的链式法则计算。这些推导可以在Ioffe和Szegedy(2015)以及多个博客中找到。24
当批量归一化应用于卷积层(第5.4节)时,原则上可以为每个像素分别计算归一化,但这会增加大量额外的可学习偏置和增益参数(βi;√i)。相反,批量归一化通常通过计算所有具有相同卷积核的像素的统计值来实现,然后为每个卷积核添加一个单独的偏置和增益参数(Ioffe和Szegedy 2015;Johnson 2020,第10讲;Zhang、Lipton等2021,第7.5节)。
在描述了批归一化在训练过程中的运作方式后,我们仍需决定测试或推理时如何处理,即当将训练好的网络应用于新数据时。我们不能简单地跳过这一阶段,因为网络是在去除常见均值和方差估计的情况下训练的。因此,通常会在整个训练集中重新计算均值和方差估计,或者使用每批统计量的某种移动平均值。由于公式(5.45)和(5.52–5.53)的线性形式,可以将μi和σi估计值以及学习到的(βi;√i)参数折叠回(5.45)中的原始权重和偏置项中。
自Ioffe和Szegedy(2015)发表开创性论文以来,已经开发出许多变体,其中一些如图5.30所示。我们不必在小批量B中的样本上累积统计量,而是在层的不同激活子集上计算它们。这些子集包括:
一层中的所有激活,称为层归一化(Ba,Kiros,和Hinton 2016);
•给定卷积输出通道中的所有激活(见第5.4节),这被称为实例归一化(Ulyanov,Vedaldi和Lempitsky2017);

图5.30来自Wu和He(2018)©2018 Springer的批次归一化、层归一化、实例归一化和组归一化。(H,W)维度表示像素,C表示通道,N表示小批量中的训练样本。蓝色的像素被相同的均值和方差归一化。
输出通道的不同子组,称为组归一化(Wu和He2018)。
吴和何(2018)的论文详细描述了这些方法,并进行了实验比较。乔、王等人(2019a)和乔、王等人(2019b)的最新研究讨论了这些新变体的一些缺点,并提出了两种新技术,即权重标准化和批量通道归一化,以缓解这些问题。
与其使用层中的激活值的统计特性来修改激活,也可以通过调整层中的权重,明确地将权重范数和权重向量方向作为独立参数,这被称为权重归一化(Salimans和Kingma 2016)。一种相关的技术称为谱归一化(Miyato、Kataoka等2018),它将每层权重矩阵的最大奇异值限制为1。
偏置和增益参数(βi,√i)也可能依赖于网络中其他层的激活,例如来自引导图像的激活。25这类技术被称为条件批量归一化,已被用于选择不同的艺术风格(Dumoulin,Shlens,和Kudlur 2017)以及在图像合成中实现局部语义引导(Park,Liu等2019)。相关内容和技术应用将在第14.6节关于神经渲染的部分详细讨论。
批处理和其他类型的归一化为何能帮助深度网络更快收敛并更好地泛化,这一问题仍在争论中。近期关于此主题的论文包括Bjorck、Gomes等人(2018年)、Hoffer、Banner等人(2018年)、Santurkar、Tsipras等人(2018年)以及Kohler、Daneshmand等人(2019年)。
注意,这使得神经网络能够乘以网络中的两个层,我们之前使用它来执行局部操作(第3.5.5节)。
为了优化神经网络中的权重,我们需要首先定义一个损失函数,然后在训练样本上最小化这个损失函数。我们在本章前面的部分已经看到了机器学习中使用的主损失函数。
对于分类任务,大多数神经网络使用最终的softmax层(5.3),如图5.27所示。由于输出值是类别概率之和为1,因此在训练过程中最小化交叉熵损失(5.19)或(5.23–5.24)作为函数是很自然的选择。在我们对前馈网络的描述中,使用索引i和j来表示神经单元,在本节中,我们将用n来索引特定的训练样本。
E(w) = En (w) = - log pntn, (5.54)
其中w是所有权重、偏置和其他模型参数的向量,pnk是网络当前对样本n属于类别k的概率估计,tn是表示正确类别的整数。将(5.20)中pnk的定义代入,并用snk替换lik(我们用于神经网络的符号),我们得到
在(w) = log Zn - sntn中 (5.55)
Zn = Σj exp snj. G mez(2018)对深度
学习中广泛使用的某些损失进行了很好的讨论。
对于执行回归的网络,即生成一个或多个连续变量,如深度图或去噪图像,通常使用L2损失,
E(w) = En (w) = - Ⅱyn - tn Ⅱ2, (5.56)
其中,yn是样本n的网络输出,tn是相应的训练(目标)值,因为这是连续变量之间误差的自然度量。然而,如果我们认为训练数据中可能存在异常值,或者粗大误差并不严重到需要二次惩罚时,可以使用更稳健的范数,如L1范数(Barron2019;Ranftl,Lasinger等2020)。(也可以在分类中使用稳健范数,例如,在类别标签中加入异常概率。)
由于通常将网络的最终输出解释为概率分布,我们需要考虑使用这些概率作为对特定答案置信度的衡量是否明智。如果网络训练得当且预测准确,这种假设是诱人的。然而,我们迄今为止介绍的训练损失却表明,
仅鼓励网络最大化概率加权的正确答案,实际上并未鼓励网络输出得到适当的置信度校准。郭、普莱斯等人(2017)讨论了这一问题,并提出了一些简单的措施,例如将对数似然乘以一个温度(Platt2000a),以改善分类器概率与真实可靠性的匹配。我们在第6.2.3节中讨论的GrokNet图像识别系统(贝尔、刘等人2020)使用校准来获得更好的属性概率估计。
对于那些产生新图像的网络,例如在引入缺失的高频细节(第10.3节)或执行图像传输任务(第14.6节)时,我们可能希望使用感知损失(Johnson,Alahi和Fei-Fei 2016;Dosovitskiy和Brox 2016;Zhang,Isola等2018),该方法利用中间层神经网络响应作为目标图像与输出图像之间比较的基础。也可以训练一个独立的判别网络来评估合成图像的质量(和合理性),如第5.5.4节所述。关于损失函数在图像合成中的应用的更多细节,请参见第14.6节中关于神经渲染的内容。
虽然损失函数传统上应用于监督学习任务中,每个输入都有正确的标签或目标值tn,但在无监督设置中也可以使用损失函数。一个早期的例子是Hadsell、Chopra和LeCun(2006)提出的对比损失函数,用于将相似的样本聚类在一起,同时将不相似的样本分散开来。更正式地说,我们给定一组输入{x}和成对指示变量{tij },这些变量表示两个输入是否相似。现在的目标是为每个输入xi计算一个嵌入vi,使得相似的输入对具有相似的嵌入(低距离),而不相似的输入则具有较大的嵌入距离。寻找能够创建有用距离的映射或嵌入被称为(距离)度量学习(Ko...stinger,Hirzer等,2012;Kulis2013),这是机器学习中常用的一种工具。用于鼓励创建此类有意义距离的损失函数统称为排序损失(G mez2019),可以用来关联来自不同领域的特征,如文本和图像(Karpathy,Joulin,和Fei-Fei2014)。
(Hadsell、Chopra和LeCun2006)定义的对比损失为
其中,P是所有标记输入对的集合,LS和LD是相似和不相似损失函数,dij = Ⅱvi - vj Ⅱ是配对嵌入之间的成对距离。
26个指示变量通常表示为yij,但为了与第5.1.3节保持一致,我们将坚持使用t ij的符号。
在度量学习中,嵌入通常被归一化为单位长度。
这与公式(5.19)给出的交叉熵损失的形式类似,只是我们测量的是编码vi和vj之间的平方距离。在他们的论文中,Hadsell、Chopra和LeCun(2006)建议使用二次函数来表示LS,并采用二次铰链损失(参见公式(5.30))。
LD = [m — dij
为了使用对比损失进行训练,你可以将两组输入通过神经网络,计算损失,然后反向传播梯度到网络的两个实例(激活)。这也可以被视为构建一个由两个共享权重的副本组成的孪生网络(Bromley,Guyon等1994;Chopra,Hadsell和LeCun 2005)。还可以构建三元组损失,该损失以一对匹配样本和一个非匹配样本作为输入,并确保非匹配样本之间的距离大于匹配样本之间距离加上某个余量(Weinberger和Saul 2009;Weston,Bengio和Usunier 2011;Schroff,Kalenichenko和Philbin 2015;Rawat和Wang 2017)。
成对对比损失和三元组损失都可以用于学习视觉相似性搜索的嵌入(Bell和Bala 2015;Wu、Manmatha等2017;Bell、Liu等2020),具体讨论见第6.2.3节。这些方法最近也被用于神经网络的无监督预训练(Wu、Xiong等2018;He、Fan等2020;Chen、Kornblith等2020),相关内容见第5.4.7节。在这种情况下,更常见的是使用受softmax(5.3)和多类交叉熵(5.20–5.22)启发的不同对比损失函数,后者最初由(Sohn 2016)提出。在计算损失之前,em-
床铺均被归一化为单位范数,Ⅱi Ⅱ2 = 1。然后,对以下损失进行求和
分母也包括了不匹配项。τ变量表示“温度”,控制聚类的紧密程度;有时它被替换为一个参数化超球半径的s乘数(Deng,Guo等,2019)。匹配计算的具体细节因具体实现而异。
这种损失有多个名称,包括InfoNCE (Oord,Li,和Vinyals 2018)和Chen,Kornblith等人(2020)提出的NT-Xent(归一化温度交叉熵损失)。广义版本的这种损失,如SphereFace、CosFace和ArcFace,在ArcFace论文(Deng,Guo等人2019)中进行了讨论和比较,并被Bell,Liu等人(2020)用于他们的视觉相似性搜索系统。Brown,Xie等人(2020)最近提出的平滑平均精度损失有时可以作为本节讨论的度量损失的替代方案。一些最近比较和讨论深度度量学习方法的论文包括(Jacob,Picard等人2019;Musgrave,Belongie和Lim 2020)。
在我们开始优化网络中的权重之前,必须先初始化它们。早期的神经网络使用小的随机权重来打破对称性,即确保所有梯度都不为零。然而,观察到在更深的层中,激活值会逐渐变小。
为了保持各层激活值的方差相当,我们必须考虑每一层的输入量,即激活值被权重乘以的传入连接数。Glorot和Bengio(2010)对此问题进行了初步分析,并建议将随机初始权重的方差设置为输入量的倒数。然而,他们的分析假设了线性的激活函数(至少在原点附近),例如tanh函数。
由于大多数现代深度神经网络使用ReLU激活函数(5.49),He、Zhang等人(2015)更新了这一分析,以考虑这种非对称的非线性。如果我们初始化层l的权重均值为零,方差为Vl,并将原始偏置设为零,则公式(5.45)中的线性求和将具有方差为
Var[sl ] = nl VlE[x], (5.59)
其中nl是传入激活/权重的数量,E[x]是期望值
平方的传入激活。当具有零均值的求和sl通过ReLU时,负数会被截断为零,因此期望值为
输出平方E[y]是sl的方差Var[sl ]的一半。
为了防止深层的平均激活量衰减或增加,我们希望连续层的激活量保持大致相同。由于我们有
(5.60)
我们得出结论,初始权重Vl的方差应该设置为
(5.61)
即,给定单元或层的扇入的一半的倒数。这种权重初始化规则通常被称为He初始化。
神经网络初始化仍然是一个活跃的研究领域,包括Kra... ...hl,Doerschhenbu等人(2016)、Mishkin和Matas(2016)、Frankle和Carbin(2019)以及Zhang、Dauphin和Ma(2019)
一旦我们确定了神经网络的层数、层宽和层深,添加了一些正则化项,定义了损失函数,并初始化了权重,就可以用样本数据训练网络了。为此,我们使用梯度下降或其变体迭代地调整权重,直到网络收敛到一组良好的值,即在训练集和验证集上的性能达到可接受水平。
为了实现这一点,我们使用链式法则计算训练样本n的损失函数En关于权重w的导数(梯度),从输出开始,逐步回溯到输入,如图5.31所示。这一过程被称为反向传播(Rumelhart,Hinton,和Williams 1986b),即错误的逆向传播。你可以在深度学习的教科书和课程笔记中找到该技术的不同描述,包括Bishop (2006,第5.3.1节)、Good- fellow,Bengio和Courville (2016,第6.5节)、Glassner (2018,第18章)、Johnson (2020,第6讲)以及Zhang、Lipton等人(2021)。
回想一下,在神经网络的前向(评估)过程中,激活值(层输出)是逐层计算的,从第一层开始,直到最后一层结束。我们将在下一节看到,许多较新的深度神经网络具有无环图结构,如图5.42–5.43所示,而不仅仅是一个单一的线性管道。在这种情况下,可以使用图的广度优先遍历。这种评估顺序的原因是为了提高计算效率。对于每个输入样本,激活值只需计算一次,并且可以在后续的计算阶段中重复使用。
在反向传播过程中,我们对反向图执行类似的广度优先遍历。
但是,我们计算的不是激活函数,而是损失函数关于权重和输入的导数,我们称之为误差。让我们从损失函数开始详细地看一下。
关于输出概率pnk的交叉熵损失En(5.54)的导数仅仅是—δntn/pnk。更有趣的是,关于进入图5.27中softmax层的分数snk(5.55)的损失的导数,
(如果使用的是one-hot编码或者目标具有非二进制概率,那么最后一种形式是很有用的。)这可以令人满意地直观解释为预测类别概率pnk与真实类别标识tnk之间的差异。

图5.31深度网络中间层反向传播导数(误差)©Glassner(2018)。损失函数对单个训练样本中每个粉色单元输入的导数相加,然后重复这一过程,逆向贯穿整个网络。
对于公式(5.56)中的L2损失,我们得到类似的结果,
在此情况下,表示预测值与目标值之间的实数差。
在本节的其余部分,我们从激活函数xin和yin中去掉样本索引n,因为每个样本n的导数通常可以独立于其他样本进行计算。28
为了计算损失项关于早期权重和激活值的偏导数,我们按照图5.31所示的方法逆向遍历网络。回顾(5.45–5.46),我们首先通过输入激活值xi与单位权重向量wi之间的点积来计算加权和si 然后,我们将这个加权和通过激活函数h,得到yi = h(si)。
计算损失En关于权重、偏置和输入的导数
激活函数,我们使用链式法则,

我们称ei =∂En/∂si为误差,即损失En相对于求和激活si的偏导数,因为它通过网络向后传播。
现在,这些错误来自哪里,即我们如何获得∂En/∂yi?回想图5.24,一个单元或层的输出成为下一层的输入。实际上,对于像图5.24中那样的简单网络,如果我们让xij表示单元i从单元j接收到的激活(而不是仅仅是单元i的第j个输入),我们可以简单地设置xij = yj。
由于yi,即单元i的输出,现在作为其他单元k > i的输入(假设这些单元是按广度优先顺序排列的),我们有
换句话说,为了计算一个单元(反向传播)的误差,我们计算来自该单元输入的误差的加权和,然后将其乘以当前激活函数h的导数(si)。这种错误的反向流动如图5.31所示,在阴影框内的三个单元的误差是通过网络后部的误差加权和计算得出的。
这个反向传播规则有一个非常直观的解释。给定单元的误差(损失的导数)取决于它所连接的单元的误差乘以它们之间的权重。这是链式法则的一个简单应用。激活函数h的斜率(si)调节了这种相互作用。如果单元的输出被限制为零或很小,例如使用负输入的ReLU或Sigmoid响应的“平坦”部分,那么该单元的误差本身也是零或很小。权重的梯度,即为了减少损失而需要调整的权重量,是传入激活和单元误差xijei的有符号乘积。这与赫布更新规则(Hebb1949)密切相关,该规则观察到生物神经元中的突触效率随着前突触处的相关放电而增加。
以及突触后细胞。一个更容易记住这个规则的方法是“如果神经元一起放电,它们就会连接在一起”(Lowel和Singer1992)。
当然,现代神经网络中还有其他计算元素,包括卷积和池化,我们将在下一节中讨论。这些单元的导数和误差传播遵循与这里概述相同的程序,即递归应用链式法则,对所应用函数求解析导数,直到得到损失函数关于所有优化参数的导数,即损失的梯度。
正如你可能已经注意到的,关于权重的梯度计算需要前向传播中计算出的单位激活值。神经网络训练的典型实现会存储给定样本的激活值,并在反向传播(误差反向传播)阶段使用这些激活值来计算权重导数。然而,现代神经网络可能有数百万个单元,因此需要存储大量的激活值(图5.44)。通过仅在某些层存储激活值,然后根据需要重新计算其余部分,可以减少需要存储的激活值数量,这种方法被称为梯度检查点(Griewank和Walther 2000;Chen,Xu等2016;Bulatov2018).29关于低内存训练的更详细综述可以在Sohoni,Aberger等(2019)的技术报告中找到。
到这一步,我们已经具备了训练神经网络所需的所有要素。我们定义了网络的拓扑结构,包括每一层的大小和深度,指定了激活函数,加入了正则化项,设定了损失函数,并初始化了权重。我们甚至描述了如何计算梯度,即正则化损失关于所有权重的导数。此时我们需要的是某种算法,将这些梯度转化为权重更新,以优化损失函数并生成一个能够很好地泛化到新未见过数据的网络。
在大多数计算机视觉算法中,如光流(第9.1.3节)、使用束调整的三维重建(第11.4.2节),甚至在较小规模的机器学习问题中,例如逻辑回归(第5.1.3节),首选的方法是线性最小二乘法(附录A.3)。优化过程采用高斯-牛顿等二阶方法,我们评估损失函数中的所有项,然后根据能量函数的梯度和海森矩阵确定方向,进行最优大小的下坡步。
不幸的是,深度学习问题过于庞大(就参数数量和训练样本而言;见图5.44),使得这种方法难以实际应用。因此,实践者开发了一系列基于随机梯度下降(SGD)扩展的优化算法(张、利普顿等,2021年,第11章)。在SGD中,我们不再像(5.54)或(5.56)那样通过累加所有训练样本来评估损失函数,而是仅评估单个训练样本n,并计算相关损失En (w)的导数。然后,沿着这个梯度的方向迈出一小步。
在实践中,从单个样本获得的方向是很好的下降方向的非常嘈杂的估计值,因此损失和梯度通常是在训练数据的一个小子集上求和,
每个子集B被称为一个迷你批次。在开始训练之前,我们随机将训练样本分配到一组固定的迷你批次中,每个批次的大小通常从低端的32到高端的8k不等(Goyal,Dollr等人,2017)。由此产生的算法称为迷你批次随机梯度下降,尽管在实际应用中,大多数人通常简称为SGD(省略了minibatches).30的引用)。
在对小批量中的样本求和后,评估梯度g=▽wEB之后,是时候更新权重了。最简单的方法是在梯度方向上迈出一小步,
w ← w — Qg or (5.72)
wt+i = wt — Qt gt (5.73)
其中第一个变体看起来更像一个赋值语句(参见,例如,Zhang,Lipton等人2021年,第11章;Loshchilov和Hutter2019),而第二个变体则明确表示时间依赖性,使用t表示梯度下降中的每个连续步骤。
步长参数Q通常被称为学习率,必须谨慎调整以确保良好的进展,同时避免过冲和梯度爆炸。实际上,通常会从较大的(但仍然较小的)学习率Qt开始,并随着时间逐渐减小,从而使优化过程收敛到一个好的最小值(Johnson 2020,第11讲;Zhang、Lipton等2021,第11章)。
在深度学习领域,经典算法中对所有测量值求和的方法被称为批量梯度下降,尽管这一术语在其他地方并不常用,因为人们普遍认为一次性使用所有测量值是更优的选择。在大规模问题如束调整中,使用小批量可能会带来更好的性能,但这一点尚未得到充分探索。

图5.32 http://playground.tensorflow.org的截图,你可以在浏览器中构建和训练自己的小型网络。由于输入空间是二维的,你可以可视化网络中每个单元对所有2D输入的响应。
常规梯度下降在当前解达到搜索空间中的“平坦点”时容易停滞,而随机梯度下降仅关注当前小批量中的误差。因此,SGD算法可能采用动量的概念,即累积并使用梯度的指数衰减(“泄漏”)运行平均值作为更新方向,
wt+i = wt - Qt vt. (5.75)
使用相对较大的P∈[0.9;0.99]值,以使算法具有良好的内存,有效地对更多批次的梯度进行平均。
在过去十年中,一些更复杂的优化技术已被应用于深度网络训练,如Johnson (2020,第11讲)和Zhang、Lipton等人(2021,第11章)所述。这些算法包括:
AdaGrad(自适应梯度),其中梯度中的每个分量除以每个分量的平方梯度之和的平方根(Duchi,Hazan,and Singer2011);
RMSProp,其中梯度平方的运行总和被替换为泄漏(衰减)总和(Hinton2012);
Adadelta,它在RMSProp的基础上增加了参数中每个组件的实际变化的泄漏总和,并在梯度重新缩放方程中使用这些参数(Zeiler 2012);
Adam将所有先前想法的元素整合到一个单一框架中,并且消除了最初泄漏估计的偏差(Kingma和Ba2015);
AdamW,即Adam与解耦权重衰减(Loshchilov和Hutter2019)。
亚当和亚当W目前是最受欢迎的深度网络优化器,尽管它们非常复杂,但为了获得良好的结果,学习率需要谨慎设置(并且可能随时间衰减)。正确设置超参数,如初始学习率、衰减速率、动量项如ρ以及正则化程度,以使网络在合理的训练时间内达到良好的性能,本身就是一个开放的研究领域。约翰逊(2020年,第11讲)的讲义提供了一些指导,但在许多情况下,人们会通过搜索超参数来找到产生最佳性能网络的方法。
一个简单的双输入示例
了解深度网络如何更新权重并在训练过程中构建解空间的一个好方法是使用http://playground.tensorflow.org.33的交互式可视化。如图5.32所示,只需点击“运行”(D)按钮开始,然后将网络重置为新的起点(运行按钮左侧),尝试逐步推进网络,使用不同数量的隐藏层单元和不同的激活函数。特别是使用ReLU时,可以看到网络如何划分输入空间的不同部分,然后将这些子部分组合在一起。第5.4.5discusses节的可视化

图5.33 LeNet- 5的架构,这是一种用于数字识别的卷积神经网络(LeCun,Bottou等,1998)©1998 IEEE。该网络在每一层使用多个通道,并交替进行多通道卷积和下采样操作,随后通过一些全连接层,为每个待分类的10个数字生成一个激活值。
前几节关于深度学习的内容涵盖了构建和训练深度网络的所有关键要素。然而,这些内容忽略了可能是图像处理和计算机视觉中最至关重要的组成部分,即使用可训练的多层卷积。卷积神经网络的概念由LeCun、Bottou等人(1998)推广,他们介绍了用于数字识别的LeNet-5网络,如图5.33.34所示。
不是将所有单元层与前一层的所有单元连接起来,卷积网络将每一层组织成特征图(LeCun,Bottou等1998),可以将其视为平行平面或通道,如图Figure5.33所示。在卷积层中,加权求和仅在一个小的局部窗口内进行,且所有像素的权重相同,这与常规平移不变图像卷积和相关性(3.12–3.15)相同。
与图像卷积不同,后者对每个(颜色)通道应用相同的滤波器,神经网络卷积通常会线性组合前一层中每个C1输入通道的激活值,并为每个C2输出通道使用不同的卷积核,如图5.34–5.35.35所示。这合乎逻辑,因为主要任务在于

图5.34多输入输出通道的二维卷积©Glassner(2018)。每个二维卷积核以前一层的所有C1个通道为输入,窗口化到一个小区域,并在下一个层的C2个通道之一中生成值(经过激活函数非线性处理后)。对于每个输出通道,我们有S2×C1个卷积核权重,因此每层可学习参数的总数为S2×C1×C2。在这个图中,我们有C1 = 6个输入通道和C2 = 4个输出通道,卷积窗口大小为S = 3,总共9×6×4个可学习权重,如图中间列所示。由于卷积应用于给定层中的每个W×H像素,因此在给定层的一个样本的一次前向和反向传播中,计算量(乘加运算)为W HS2 C1 C2。
卷积神经网络层用于构建局部特征(图3.40c),然后以不同的方式组合这些特征,以产生更具区分性和语义意义的特征。第5.4.5节中的图5.47展示了深度网络提取的各种特征的可视化。
有了这些直觉,我们就可以将卷积层中执行的加权线性求和(5.45)写成
其中x(i,j,c1)是前一层的激活值,正如公式(5.45)所示,N是二维空间核中的S2符号偏移量,符号c1∈{C1 }表示c1∈[0,C1 )。需要注意的是,由于偏移量(k,l)被加到(i,j)像素坐标上(而不是从其减去),这一操作实际上是一个相关运算(3.13),但这种区别通常被忽略。

图5.35具有多个批次、输入和输出通道的二维卷积,©John-
(2020)。在进行小批量梯度下降时,整个批次的训练图像或
特征被传递到一个卷积层,该层以所有Cin通道作为输入
前一层被窗口化到一个小区域,并产生值(在激活之后
在下一层的Cout通道中,函数非线性)之一。和之前一样,对于每一个
输出通道中,我们有Kw×Kh×Cin内核权重,因此每个卷积层中可学习参数的总数为Kw×Kh×Cin×Cin。在该图中,我们有Cin = 3个输入通道和Cout = 6个输出通道。
在神经网络图中,如图5.33和5.39–5.43所示,通常会标明卷积核大小S和层中的通道数C,有时也会显示图像尺寸,例如图5.33和5.39。请注意,某些神经网络,如GoogLeNet (Szegedy,Liu等,2015)中的Inception模块,如图5.42所示,使用1×1的卷积,这些卷积实际上并不执行卷积操作,而是按像素合并不同的通道,通常目的是降低特征空间的维度。
因为卷积核中的权重对于给定层和通道内的所有像素都是相同的,这些权重实际上是在绘制不同层中不同像素之间所有连接时共享的。这意味着需要学习的权重远少于全连接层。这也意味着在反向传播过程中,核权重更新会在给定层/通道的所有像素上求和。
为了完全确定卷积层的行为,我们仍然需要指定一些
•填充。早期网络如LeNet-5没有对图像进行填充,因此每次卷积后图像都会缩小。现代网络可以选择指定填充宽度和模式,使用传统图像处理中常用的选择之一,如零填充或像素复制,如图3.13所示。
•步长。卷积的默认步长为1像素,但也可以仅在每第n列和行处评估卷积。例如,AlexNet中的第一个卷积层(图5.39)使用了4的步长。传统的图像金字塔(图3.31)在构建较粗层次时使用2的步长。
膨胀。可以在像素之间插入额外的“空间”(跳过行和列)
卷积过程中的样本,也被称为膨胀或孔(在法语中,有孔的意思)
通常只是“无”卷积(Yu和Koltun2016;Chen,Papandreou等人2018)。虽然原则上这可能导致混叠,但它也可以在使用更少的操作和可学习参数的情况下有效地对更大的区域进行池化。
•分组。默认情况下,所有输入通道用于生成每个输出通道,但也可以将输入和输出层分成G个独立的组,每组分别进行卷积(Xie,Girshick等,2017)。G = 1对应常规卷积,而G = C1表示每个对应的输入通道独立于其他通道进行卷积,这被称为深度卷积或通道分离卷积(Howard,Zhu等,2017;Tran,Wang等,2019)。
由Vincent Dumoulin创建的这些不同参数的效果的动画可以在https://github.com/vdumoulin/conv arithmeticas以及Dumoulin和Visin(2016)中找到。
在某些应用中,如图像修复(第10.5.1节),输入图像可能附带一个二值掩模,指示哪些像素是有效的,哪些需要填充。这类似于我们在第3.1.3节中研究的透明度图像概念。在这种情况下,可以使用部分卷积(Liu,Reda等人,2018年),其中输入像素与掩模像素相乘,然后根据非零掩模像素的数量进行归一化。如果任何输入掩模像素为非零,则掩模通道输出设为1。这类似于我们图4.2中展示的Gortler,Grzeszczuk等人(1996年)提出的拉推算法,不同之处在于卷积权重是学习得到的。
更复杂的部分卷积版本是门控卷积(Yu,Lin等人。
2019;Chang,Liu等2019),其中每个像素的掩码通过学习卷积后接sigmoid非线性函数从前一层获得。这使得网络不仅能够更好地学习每个像素的信心度量(权重),还能融入额外的特征,如用户绘制的草图或推导出的语义信息。
正如我们在卷积讨论中所见,步长大于1可以用来降低给定层的分辨率,例如AlexNet的第一个卷积层(图5.39)。当卷积核内的权重相等且总和为1时,这被称为平均池化,通常以通道方式应用。
广泛使用的一种变体是在方形窗口内计算最大响应,这被称为最大池化。最大池化的常见步长和窗口大小包括步长为2和2×2非重叠窗口或3×3重叠窗口。最大池化层可以视为“逻辑或”,因为它们只需要池化区域中的一个单元被激活即可。它们还应该提供输入的某种平移不变性。然而,大多数深度网络并不是完全平移不变的,这会降低其性能。张(2019)的论文对此问题进行了很好的讨论,并提出了一些简单的建议来缓解这一问题。
一个常见的问题是,如何通过最大池化层进行反向传播。
最大池化操作符就像一个“开关”,将输入单元之一连接到输出单元。因此,在反向传播过程中,只要我们记得哪个单元有这种响应,就只需要将误差和导数传递给这个最活跃的单元。
同样的最大池化机制可以用来创建一个“反卷积网络”
在寻找最能激活特定单元的刺激物(图5.47)时(Zeiler和Fergus2014)。
如果我们希望行为更加连续,可以构建一个池化单元,该单元对其输入计算Lp范数,因为Lp→∞实际上是在其组件上计算最大值(Springenberg,Dosovitskiy等,2015)。然而,这样的单元需要更多的计算,因此在实际应用中并不广泛使用,除非有时用于最后一层,在这种情况下被称为广义均值(GeM)池化(Doll r,Tu等,2009;Tolias,Sicre和J gou,2016;Gordo,Almazn等,2017;Radenovi,Tolias

图5.36转置卷积(©Dumoulin和Visin(2016))可用于放大(增加尺寸)图像。在应用卷积算子之前,在输入样本之间插入(s - 1)个额外的零行和零列,其中s是放大步长。
虽然池化可以用来(近似地)逆转最大池化操作的效果,但如果我们想逆转卷积层,可以参考我们在第3.5.1节和第3.5.3节中研究的插值算子的学习变体。最直观的方法是在输入层的像素之间添加额外的零行和零列,然后运行常规卷积(图5.36)。这种操作有时被称为分数步长的反向卷积(Long、Shelhamer和Darrell 2015),尽管更常见的名称是转置卷积(Dumoulin和Visin 2016),因为当卷积以矩阵形式表示时,这个操作相当于与一个转置稀疏权重矩阵相乘。与常规卷积一样,可以指定填充、步幅、膨胀和分组参数。然而,在这种情况下,步幅指定的是图像上采样而不是下采样的倍数。
U-网和特征金字塔网络
在讨论第3.5.3节中的拉普拉斯金字塔时,我们看到了如何结合图像下采样和上采样来实现多种多分辨率图像处理任务(图3.33)。同样的组合方法也可以用于深度卷积网络中,特别是当我们希望输出是一个全分辨率图像时。这类应用的例子包括像素级语义标注(第6.4节)、图像降噪和超分辨率(第10.3节)、单目深度推断(第12.8节)以及神经风格迁移(第14.6节)。降低网络分辨率后再重新扩展的想法有时被称为瓶颈,这与早期使用自编码器进行的自监督网络训练有关(Hinton和Zemel 1994;Goodfellow、Bengio和Courville 2016,第14章)。
这一想法最早的应用之一是开发的全卷积网络

图5.37(a)Noh、Hong和Han(2015)的去卷积网络©2015 IEEE和(b—c)Ronneberger、Fischer和Brox(2015)的U-Net,使用PlotNeural- Net LaTeX包绘制。除了(a)中使用的细到粗再到细的瓶颈外,U-Net在相同分辨率下还具有编码层和解码层之间的跳跃连接。

图5.38来自https://cs.stanford. edu/people/karpathy/convnetjs的Andrej Karpathy网页浏览器演示的截图,在这里你可以运行一些小型神经网络,包括用于数字和微型图像分类的CNN。
由Long、Shelhamer和Darrell(2015)提出。这篇论文启发了众多后续架构,包括Noh、Hong和Han(2015)提出的沙漏形状的“反卷积”网络,Ronneberger、Fischer和Brox(2015)提出的U-Net,Chen、Papandreou等人(2018)提出的具有CRF精炼层的空洞卷积网络,以及Kirillov、Girshick等人(2019)提出的全景特征金字塔网络。图5.37展示了其中两种网络的一般布局,相关内容将在第6.4节关于语义分割中详细讨论。我们将在后续章节中看到这些骨干网络(He、Gkioxari等人,2017)在图像去噪和超分辨率(第10.3节)、单目深度推断(第12.8节)和神经风格迁移(第14.6节)中的其他应用。
卷积神经网络最早的商业应用之一是LeCun、Bottou等人(1998)创建的LeNet-5系统,其架构如图5.33所示。该网络包含了现代卷积神经网络的大部分元素,尽管它使用了sigmoid非线性、平均池化和高斯RBF单元,而不是输出层的softmax。如果你想尝试这个简单的数字识别卷积神经网络,可以访问由Andrej Karpathy在https://cs.stanford.edu/people/karpathy/ convnetjs上创建的交互式JavaScript演示(图5.38)。
该网络最初于1995年左右由AT&T部署,用于自动读取存入NCR ATM机的支票,以验证书面和按键支票金额是否相同。该系统随后被纳入NCR的高速支票读取系统,

图5.39 SuperVision深度神经网络(更常被称为“AlexNet”)的架构,由Matt Deitke提供(改编自Krizhevsky、Sutskever和Hinton 2012)。该网络由多个带有ReLU激活函数的卷积层、最大池化层、一些全连接层以及一个用于生成最终类别概率的softmax层组成。
在某个时候,它处理了美国所有支票的10%到20%。
今天,LeNet-5架构(图5.33)的变体常被用作该主题课程和教程中介绍的第一个卷积神经网络。尽管最初用于训练LeNet-5的MNIST数据集(LeCun、Cortes和Burges 1998)有时仍被使用,但更常见的是使用更具挑战性的CIFAR-10(Krizhevsky 2009)或Fashion MNIST (Xiao、Rasul和Vollgraf 2017)作为训练和测试的数据集。
虽然现代卷积神经网络最早在20世纪90年代末开发并部署,但直到克里谢夫斯基、苏特塞弗和欣顿(2012年)的突破性发表,它们才开始在自然图像分类方面超越传统技术(图5.40)。如图所示,AlexNet系统(他们超级视觉网络的更常用名称)将错误率从25.8%大幅降至16.4%。随后几年里,由于进一步的发展以及使用更深的网络,例如从最初的8层AlexNet到152层ResNet,性能又迅速取得了显著提升。
图5.39显示了SuperVision网络的体系结构,其中包含一系列
具有ReLU(修正线性)非线性、最大池化和一些全连接层的卷积层

图5.40 ImageNet中获胜参赛作品的前5个错误率和网络深度
大规模视觉识别挑战(ILSVRC)©Li、Johnson和Yeung(2019)。
连接层,以及一个最终的softmax层,该层被输入到多类交叉熵损失中。Krizhevsky、Sutskever和Hinton(2012)还使用了dropout(图5.29)、小的平移和颜色操作进行数据增强、动量和权重衰减(L2权重惩罚)。
本文发表后的几年里,图像识别大规模视觉挑战赛(Rus- sakovsky,Deng等,2015)上的分类性能有了显著提升,如图5.40所示。关于这些不同网络的创新之处、其能力和计算成本的详细描述,可以在贾斯汀·约翰逊(2020年,第8讲)的讲座幻灯片中找到。
2013年,Zeiler和Fergus(2014)的获奖作品使用了更大版本的AlexNet,在卷积阶段增加了更多的通道,将错误率降低了约30%。2014年,牛津视觉几何小组(VGG)的获奖作品由Simonyan和Zisserman(2014b)提出,该作品采用了重复的3×3卷积/ReLU块,穿插2×2最大池化和通道加倍(图5.41),随后是一些全连接层,生成了16到19层的网络,进一步将错误率降低了40%。然而,如图5.44所示,这种性能提升是以计算量大幅增加为代价的。
2015年,Szegedy、Liu等人(2015)的GoogLeNet则专注于效率。Goog- LeNet首先采用了一个激进的主干网络,通过一系列步幅卷积和常规卷积以及最大池化层,迅速将图像分辨率从224×224降至282×282。随后,它使用了多个Inception模块(图5.42),每个模块都是一个小分支神经网络,其特征在最后被连接起来。该模块的一个重要特点是使用1×1“瓶颈”卷积来减少数量。

图5.41 Simonyan和Zisserman(2014b)©Glassner(2018)的VGG16网络。
(a)网络由重复的零填充、3×3卷积、ReLU模块组成,其间穿插着2×2最大池化和通道数翻倍。随后是全连接层和丢弃层,最后通过softmax函数映射到1,000个ImagetNet类别。
(b)Glassner(2018)使用的部分示意图神经网络符号。

图5.42来自(Szegedy,Liu的初始模块 (et al.2015)©2015 IEEE,它将降维、多个卷积大小和最大池化作为不同的通道堆叠在一起,形成最终特征图。

图5.43 ResNet残差网络(He,Zhang .etal2016a)©2016 IEEE,展示了绕过一系列卷积层的跳跃连接。右侧图使用瓶颈来减少卷积前的通道数。直接连接可以捷径绕过卷积层,使得梯度在训练过程中更容易反向流经网络。
在执行较大的3×3和5×5卷积之前,先进行通道操作,从而节省了大量计算。这种投影后接额外卷积的方法,在精神上类似于Perona(1995)提出的将滤波器近似为可分离卷积之和的方法。GoogLeNet还去除了末端的全连接(MLP)层,转而采用全局平均池化后接一个线性层再进行softmax操作。其性能与VGG相似,但计算量和模型大小的成本显著降低(图5.44)。
次年,残差网络(He,Zhang等,2016a)问世,显著扩展了可成功训练的层数(图5.40)。主要的技术创新是引入了跳跃连接(最初称为“捷径连接”),这使得信息(和梯度)能够在一组卷积层之间流动,如图5.43所示。这些网络被称为残差网络,因为它们允许网络学习一组输入和输出激活之间的残差(差异)。基本残差块的一个变体是图5.43右侧所示的“瓶颈块”,它在执行3×3卷积层之前减少通道数。进一步的扩展,如(He,Zhang等,2016b)所述,将ReLU非线性移至残差求和之前,从而无需额外成本即可建模真正的恒等映射。
为了构建ResNet,各种残差块与步幅卷积和通道加倍交织在一起,以达到所需的层数。(类似于GoogLeNet中使用的下采样茎和平均池化softmax层,在开头和结尾处使用。)通过组合不同数量的残差块,已经构建并评估了包含18、34、50、101和152层的ResNet。更深的网络具有更高的精度。
但计算成本更高(图5.44)。2015年,ResNet不仅在ILSVRC(ImageNet)分类、检测和定位挑战中排名第一,在更新的COCO数据集和基准测试中的检测和分割挑战中也排名第一(Lin,Maire等人,2014)。
自那时起,各种扩展和变体被构建并进行了评估。谢、吉什克等人(2017)提出的ResNeXt系统使用分组卷积略微提高了准确性。密集连接的CNN(黄、刘等人,2017)在非相邻卷积块和/或池化块之间添加了跳跃连接。最后,胡、沈、孙等人(2018)提出的挤压与激励网络(SENet)通过全局上下文(通过全局池化)加入每一层,显著提升了准确率。关于这些及其他CNN架构的更多信息,可以在原始论文以及本主题的课堂笔记中找到(李、约翰逊和杨2019;约翰逊2020)。
移动网络
随着深度神经网络变得越来越深、越来越大,一种相反的趋势出现了,即构建更小、计算成本更低的网络,这些网络可以用于移动和嵌入式应用。最早为轻量级执行定制的网络之一是MobileNets (Howard,Zhu等,2017),该网络使用了深度卷积,这是分组卷积的一个特例,其中组的数量等于通道数。通过调整两个超参数,即宽度乘数和分辨率乘数,网络架构可以在精度、尺寸和计算效率之间进行权衡。随后的MobileNetV2系统(Sandler,Howard等,2018)增加了一个“倒残差结构”,其中捷径连接位于瓶颈层之间。ShuffleNet(Zhang,Zhou等,2018)在分组卷积之间增加了一个“洗牌”阶段,以使不同组中的通道能够混合。ShuffleNet V2 (Ma,Zhang等,2018)增加了通道分割操作符,并使用端到端性能指标来调整网络架构。另外两个为提高计算效率而设计的网络是ESPNet (Mehta,Rastegari等,2018)和ESPNetv2 (Mehta,Rastegari等,2019),它们使用了(深度-宽)扩张可分离卷积的金字塔结构。
分组、深度和通道分离卷积的概念仍然是管理计算效率和模型大小的广泛使用的工具(Choudhary,Mishra等人,2020),不仅在移动网络中,而且在视频分类中(Tran,Wang等人。
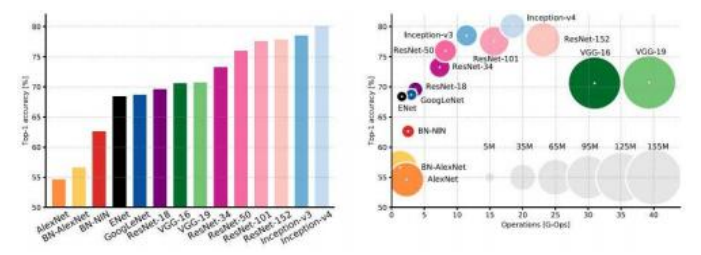
图5.44网络精度与规模及操作次数的关系(Canziani,Culurciello和Paszke2017)©2017 IEEE:在右侧图中,网络精度与操作次数(1—40 G-Ops)的关系被绘制出来,而圆圈的大小表示参数的数量(10—155 M)。BN表示网络的批量归一化版本。
尝试这些不同的CNN架构的一个好方法是从模型库下载预训练模型,例如https://github.com/pytorch/视觉中的TorchVision库。如果你查看torchvision/models文件夹,你会发现AlexNet、VGG、GoogleNet、Inception、ResNet、DenseNet、MobileNet和ShuffleNet等模型的实现,以及其他用于分类、目标检测和图像分割的模型。更近期的一些模型,将在后续章节中讨论,可以在PyTorch图像模型库(timm)中找到,该库还提供了https://github.com/rwightman/pytorch-image-models.类似的预训练模型集合。对于其他语言,也有类似的预训练模型集合,例如https://www.tensorflow.org/lite/models,用于高效的(移动)TensorFlow模型。
虽然人们经常下载并使用预训练的神经网络来实现他们的应用,但更常见的是至少在与应用特性更为相关的数据上微调这些网络(而不是大多数动物园模型所基于的公共基准数据)。同样,也很常见的是替换网络的最后一层,即头部(之所以这样称呼,是因为当各层从下往上堆叠时,它位于图中的顶部),而保留骨干部分不变。骨干和头部(s)这两个术语被广泛使用,并由Mask-RCNN论文(He,Gkioxari等,2017)推广开来。一些较新的论文
将主干和头部称为躯干及其分支(Ding和Tao2018;Kirillov、Girshick等人2019;Bell、Liu等人2020),有时也使用颈部一词(Chen、Wang等人2019)。43
当添加新的头部时,可以使用特定于预期应用的新数据来训练其参数。根据可用的新训练数据的数量和质量,头部可以简单到线性模型,如SVM或逻辑回归/软最大值(Donahue,Jia等,2014;Sharif Razavian,Azizpour等,2014),也可以复杂到全连接网络或卷积网络(Xiao,Liu等,2018)。调整主干中的一些层也是一个选项,但需要足够的数据和较慢的学习率,以确保预训练的好处不会丧失。在一个数据集上预训练机器学习系统,然后将其应用于另一个领域的过程称为迁移学习(Pan和Yang,2009)。我们将在第5.4.7节关于自监督学习的部分更详细地讨论迁移学习。
模型尺寸和效率
正如前文所述,神经网络模型的规模(通常以参数数量,即权重和偏置的数量来衡量)和计算负载(通常以每前向推理一次的浮点运算次数来衡量)种类繁多。C anziani、C ulcerciello和Paszke(2017)的评估总结在图5.44中,展示了2012年至2017年间在ImageNet挑战中表现最佳的网络的性能(准确性和规模+操作)。除了我们已经讨论过的网络外,该研究还包括Inception-v3 (Szegedy、Vanhoucke等2016)和Inception-v4 (Szegedy、Ioffe等2017)。
因为深度神经网络可能非常依赖内存和计算资源,许多研究人员已经研究了减少这两方面的方法,使用较低精度(例如定点)算术和权重压缩(Han,Mao,和Dally 2016;Iandola,Han等2016)。Rastegari,Ordonez等人(2016)在XNOR-Net论文中探讨了使用二进制权重(开关闭合连接)以及可选的二进制激活函数。该论文还对先前的二进制网络和其他压缩技术进行了很好的综述,最近的调查论文也是如此(Sze,Chen等2017;Gu,Wang等2018;Choudhary,Mishra等2020)。
神经网络设计的最新趋势之一是使用神经架构搜索(NAS)算法来尝试不同的网络拓扑和参数化(Zoph

图5.45图像网络准确率与(a)大小(参数数量)和(b)操作次数的关系,针对一些近期高效的网络(Wan,Dai等人,2020)©2020 IEEE。
以及Le2017;Zoph,Vasudevan等人2018;Liu,Zoph等人2018;Pham,Guan等人2018;Liu,Simonyan和Yang2019;Hutter,Kotthoff和Vanschoren2019)。这一过程比早期网络设计中常见的试错方法更高效(就研究人员的时间而言)。Elsken,Metzen和Hutter(2019)综述了这些以及更多关于这一快速发展的主题的论文。最近的出版物包括FBNet (Wu,Dai等人2019)、RandomNets(Xie,Kirillov等人2019)、EfficientNet(Tan和Le2019)、RegNet (Radosavovic,Kosaraju等人2020)、FBNetV2(Wan,Dai等人2020)和EfficientNetV2(Tan和Le2021)。还可以进行无监督神经架构搜索(Liu,Dollr等人2020)。图5.45显示了ImageNet
上的前1%准确率与网络大小(参数数量)及前向推理操作次数的关系,针对多个近期的网络架构(Wan,Dai等人2020)。与图5.44所示的早期网络相比,较新的网络使用了10×(或更多)更少的参数。
深度学习软件
在过去十年中,大量深度学习软件框架和编程语言扩展被开发出来。维基百科上的深度学习软件条目列出了二十多个这样的框架,其中大约一半仍在积极开发中。44尽管Caffe (Jia,Shelhamer等2014)是最早用于计算机视觉应用的框架之一,但它大多已被PyTorch和TensorFlow所取代,至少从现在大多数计算机视觉研究论文附带的开源实现来看是这样。

图5.46由Geoffrey Hinton提供的一个Hinton图,显示了三层神经网络中连接各个单元的权重。每个小方框的大小表示每个权重的大小,颜色(黑色或白色)表示符号。
安德鲁·格拉斯纳(2018)的深度学习入门书籍使用了Keras库,因为其简洁性。《深入浅出的深度学习》(张、利普顿等,2021)及其配套课程(斯莫拉和李,2019)在文中所有示例中均使用了MXNet,但最近他们也发布了PyTorch和TensorFlow代码示例。斯坦福大学的CS231n(李、约翰逊和杨,2019)和约翰逊(2020)包括了一门关于PyTorch和TensorFlow基础原理的讲座。一些课程还使用了简化框架,要求学生实现更多组件,例如麦克阿莱斯特(2020)开发并在盖格(2021)中使用的教育框架(EDF)。
除了软件框架和库之外,深度学习代码开发通常还能受益于优秀的可视化库,如TensorBoard和Visdom。此外,除了本节前面提到的模型动物园,还有更高级别的包,例如Classy Vision,这些包允许你无需或仅需少量编程即可训练或微调自己的分类器。安德烈·卡帕西还在http://karpathy.github.io/2019/04/25/recipe提供了一份有用的神经网络训练指南,这可能有助于避免常见问题。
可视化中间结果和最终结果一直是计算机视觉算法开发的重要组成部分(例如图1.7-1.11),是培养直觉、调试或优化结果的极佳方式。在本章中,我们已经看到了一些简单的工具示例
两输入神经网络可视化,例如图5.32中的TensorFlow Playground和图5.38中的ConvNetJS。在本节中,我们讨论用于可视化网络权重的工具,更重要的是,用于可视化网络中不同单元或层的响应函数的工具。
对于如图5.32所示的简单小网络,我们可以使用线条宽度和颜色来表示连接的强度。那么,对于包含更多单元的网络呢?一种巧妙的方法是用不同大小的黑框或白框来表示输入和输出权重的强度,这种方法以发明者的名字命名为欣顿图,如图5.46所示(Ackley,Hinton,和Sejnowski 1985;Rumelhart,Hinton,和Williams 1986b)。
如果我们希望展示给定层中的激活集,例如MNIST或CIFAR-10中最后10分类层的响应,在某些输入或所有输入上,我们可以使用非线性降维技术,如第5.2.4节和图5.21中讨论的t-SNE和UMap。
我们如何可视化深度网络中各个单元(“神经元”)的响应?对于网络的第一层(图5.47左上角),可以直接从给定通道的输入权重(灰色图像)读取响应。我们还可以找到验证集中产生最大响应的区域,这些区域对应于给定通道中的各个单元(图5.47左上角的彩色区域)。(记住,在卷积神经网络中,特定通道中的不同单元对输入的平移版本有相似的响应,忽略边界和混叠效应。)
对于网络的深层,我们可以在输入图像中再次找到最大激活区域。一旦找到这些区域,Zeiler和Fergus(2014)将一个反卷积网络与原始网络配对,以反向传播特征激活,一直追溯到图像区域,从而在图5.47的第2到第5层生成灰度图像。Springenberg、Dosovitskiy等人(2015)开发的一种相关技术称为引导反向传播,可以产生略高的对比度结果。
另一种探究卷积神经网络特征图的方法是确定输入图像的各个部分在给定通道中激活单元的程度。Zeiler和Fergus(2014)通过用一个灰色方块遮挡输入图像的子区域来实现这一点,这不仅生成了激活图,还能显示每个图像区域最可能的标签(图5.48)。Si- monyan、Vedaldi和Zisserman(2013)描述了一种相关的技术,称为显著性图;Nguyen、Yosinski和Clune(2016)将其称为激活最大化;Selvaraju、Cogswell等人(2017)则将其可视化技术称为梯度加权类激活映射(Grad-CAM)。

Springer。每个可视化的卷积层都来自一个从Su-
Krzhevsky、Sutskever和Hinton(2012)提出的perVision。3×3子图像表示
将一个特征图(给定层中的通道)中的前9个响应投影回像素
空间(较高层投影到更大的像素块),右侧显示彩色图像
从验证集中提取响应最灵敏的图像补丁,左边的灰色带符号的图像显示了相应的最大刺激前图像。

图5.48来自Zeiler和Fergus(2014)的热图可视化©2014斯普林格。通过用一个小灰方块覆盖输入图像的部分区域,可以可视化第5层中高度活跃通道的响应(第二列),以及特征图投影(第三列)、正确类别的可能性和每个像素最可能的类别。

图5.50对抗图像示例©Szegedy,Zaremba (2013)。对于左列中的每张原始图像,在中间列中添加一个小的随机扰动(放大10×),以获得右列中的图像,该图像总是被分类为鸵鸟。
许多关于可视化神经网络响应和行为的技术已在各种论文和博客中被描述(Mordvintsev,Olah和Tyka 2015;Zhou,Khosla等2015;Nguyen,Yosinski和Clune 2016;Bau,Zhou等2017;Olah,Mordvintsev和Schubert 2017;Olah,Satyanarayan等2018;Camarata,Carter等2020),以及约翰逊(2020,第14讲)的大量讲座幻灯片。图5.49展示了一个例子,展示了预训练的GoogLeNet中的不同层。OpenAI最近还发布了一个名为Microscope的优秀交互工具,49让人们能够可视化许多常见神经网络中每个神经元的重要性。
虽然诸如引导反向传播等技术可以帮助我们更好地可视化神经网络的响应,但它们也可以通过微妙地扰动输入来“欺骗”深度网络,使其错误分类,如图5.50所示。创建此类图像的关键是取一组最终激活值,然后沿“假”类别方向反向传播梯度,更新输入图像,直到假类别成为主导激活。Szegedy、Zaremba等人(2013)将这种扰动的图像称为对抗样本。
运行这个反向传播需要访问网络及其权重,这意味着这是一个白盒攻击,而不是黑盒攻击,在黑盒攻击中,什么都没有
但令人惊讶的是,作者发现“……对抗性示例相对稳健,并且被具有不同层数、激活或在训练数据的不同子集上训练的神经网络共享。”
最初的对抗性攻击发现引发了一系列额外的研究(Goodfellow,Shlens和Szegedy 2015;Nguyen,Yosinski和Clune 2015;Kurakin,Good-fellow和Bengio 2016;Moosavi-Dezfooli,Fawzi和Frossard 2016;Goodfellow,Paper-not等2017)。Eykholt、Evtimov等人(2018)展示了如何通过向现实世界中的物体(如停车标志)添加简单的贴纸,导致神经网络错误分类这些物体的照片。Hendrycks、Zhao等人(2021)创建了一个自然图像数据库,这些图像能够持续欺骗在ImageNet上训练的流行深度分类网络。尽管对抗样本主要用于展示深度学习模型的弱点,但它们也可以用于提高识别能力(Xie,Tan等人2020)。
伊利亚斯、桑图尔卡尔等人(2019)试图揭开对抗样本的神秘面纱,发现这些样本并非像预期那样产生影响人类标签的大规模扰动,而是执行了一种捷径学习(拉普什金、瓦……德琴等人2019;盖尔霍斯、雅各布森等人2020)。他们发现优化器利用了图像标签中的非鲁棒特征;即数据集中存在的、但不易被人类察觉的图像类别的非随机相关性。这些非鲁棒特征对人类观察者来说只是噪声,使得受其扰动的图像大多相同。他们的观点得到了仅基于非鲁棒特征训练分类器的支持,并且发现这些特征与图像分类性能相关。
是否存在防范对抗性攻击的方法?聪明人软件库(Papernot,Faghri等,2018)提供了对抗样本构建技术和对抗训练的实现。此外,还有一篇关于机器学习中安全与隐私的http://www.cleverhans.ioblog文章。Madry,Makelov等(2018)展示了如何训练一个网络,使其对已知测试图像中的有界加性扰动具有鲁棒性。最近的研究还包括通过迫使扰动后的图像在视觉上与其(虚假)目标类别相似来检测(Qin,Frosst等,2020b)和防御对抗性攻击(Qin,Frosst等,2020a)。这一领域仍在不断发展中,对于基于机器学习的应用程序的鲁棒性和安全性有着深远的影响,数据集偏差问题(Torralba和Efros,2011)也可以通过测试跨数据集迁移性能在一定程度上加以防范(Ranftl,Lasinger等,2020)。
正如我们之前提到的,为一个任务(例如,全图像分类)预先训练一个主干(或躯干)网络是很常见的,然后用一个
新的头部(或一个或多个分支),然后对其进行不同的任务训练,例如,语义图像分割(He,Gkioxari等人,2017)。可选地,原始主干网络的最后几层可以进行微调。
将一个任务的训练结果应用于另一个任务的想法被称为迁移学习,而将最终网络调整到其预期应用和统计特性的过程则称为领域适应。尽管这一理念最初是应用于在标记数据集如ImageNet上训练的骨干网络,即完全监督的方式,但预训练于数量庞大的未标记真实世界图像集的可能性始终是一个诱人的选择。
自监督学习的核心思想是创建一个监督预设任务,其中标签可以从未标记的图像中自动推导出来,例如通过让网络预测其余信息的一部分。预训练完成后,网络可以被修改并微调以适应最终的下游任务。Weng(2019)对此主题有一篇精彩的入门博客文章,而Zisserman(2018)则有一场精彩的讲座,在其中使用了“代理任务”这一术语。此外,Jing和Tian(2020)的综述和Ren(2020)的参考书目中也有很好的介绍。
图5.51显示了一些为预处理而提出的借口任务示例
训练图像分类网络。这些包括:
背景预测(Doersch、Gupta和Efros2015):获取附近的图像块并预测它们的相对位置。
背景编码器(Pathak,Krahenbuhl等人,2016):修复图像中一个或多个缺失区域。
9块拼图(Noroozi和Favaro2016):将拼图重新排列到正确的位置。
彩色化黑白图像(Zhang、Isola和Efros2016)。
通过以90°的倍数旋转图像使其竖直(Gidaris、Singh和Ko- modakis2018)。该论文将自己与11种先前的自监督技术进行了比较。
除了使用单图像预设任务外,许多研究人员还使用了视频片段,因为连续的帧包含语义相关的内容。一种利用这些信息的方法是按时间顺序正确排列视频帧,即使用时间版本的情境预测和拼图(Misra,Zitnick和Hebert 2016;Wei,Lim等2018)。另一种方法是将着色扩展到视频中,首先给定第一帧的颜色(Vondrick,

图5.51自监督学习任务示例:(a)猜测图像块的相对位置——你能猜出Q1和Q2的答案吗?(Doersch、Gupta和Efros 2015)©2015 IEEE;(b)解决九片拼图(Noroozi和Favaro 2016)©2016斯普林格;(c)图像着色(Zhang、Isola和Efros 2016)©2016斯普林格;(d)视频颜色转移用于跟踪(Vondrick、Shrivastava等2018)©2016斯普林格。
Shrivastava等人(2018)提出的方法鼓励网络学习语义类别和对应关系。由于视频通常伴有声音,这些声音可以作为自监督的额外线索,例如通过让网络对齐视觉和音频信号(Chung和Zisserman 2016;Arandjelovic和Zisserman 2018;Owens和Efros 2018),或在无监督(对比)框架中使用(Alwassel、Mahajan等2020;Patrick、Asano等2020)。
由于自监督学习显示出了巨大的前景,一个开放的问题是,这些技术是否能在某个时候超越在较小的全标记数据集上训练的完全监督网络的性能。50一些令人印象深刻的结果已经使用
半监督(弱)学习(第5.2.5节)在非常大的(300M–3.5B)部分或噪声标记数据集上进行,例如JFT-300M (Sun,Shrivastava等人,2017年)和Instagram标签(Mahajan,Girshick等人,2018年)。其他研究者尝试同时使用监督学习处理已标记数据和自监督预设任务学习处理未标记数据(Zhai,Oliver等人,2019年;Sun,Tzeng等人,2019年)。事实证明,要充分利用这些方法,需要仔细关注数据集大小、模型架构和容量,以及预设任务的细节(和难度)(Kolesnikov,Zhai,和Beyer,2019年;Goyal,Mahajan等人,2019年;Misra和Maaten,2020年)。与此同时,还有人致力于研究预训练在下游任务中实际带来的真正益处(He,Girshick,和Doll等人,2019年;Newell和Deng,2020年;Feichtenhofer,Fan等人,2021年)。
半监督训练系统自动为预设任务生成真实标签,以便这些标签可以被用于监督学习(例如,通过最小化分类错误)。另一种方法是使用无监督学习结合对比损失(Section5.3.4)或其他排序损失(G mez2019),以鼓励语义相似的输入产生相似的编码,同时将不相似的输入进一步分离。
这通常现在被称为对比(度量)学习。
吴、熊等人(2018)训练一个网络,为每个实例(训练样本)生成独立的嵌入向量,并将其存储在移动平均内存库中,随着新样本通过正在训练的神经网络输入。然后,他们使用嵌入空间中的最近邻来分类新图像。动量对比(MoCo)用固定长度的编码样本队列替代内存库,这些样本通过时间适应的动量编码器输入,该编码器与实际训练的网络分开(何、范等人2020)。预文本不变表示学习(PIRL)使用预文本任务和“多裁剪”数据增强,但随后使用内存库和对比损失比较它们的输出(米斯拉和马滕2020)。简单对比学习框架(SimCLR)使用固定的迷你批次,并在批次中的每个样本与其他所有样本之间应用对比损失(归一化温度交叉熵,类似于公式(5.58)),同时进行激进的数据增强(陈、科尔布利斯等人2020)。MoCo v2结合了MoCo和SimCLR的思想,以获得更好的结果(陈、范等人2020)。而不是直接比较生成的嵌入向量,首先应用一个全连接网络(MLP)。
对比损失是度量学习中的一个有用工具,因为它鼓励嵌入空间中语义相关的输入之间的距离较小。另一种方法是使用深度聚类来同样鼓励相关输入产生相似的输出(Caron,Bo- janowski等2018;Ji,Henriques和Vedaldi 2019;Asano,Rupprecht和Vedaldi 2020;Gidaris,Bursuc等2020;Yan,Misra等2020)。一些最新的使用聚类进行无监督学习的结果现在可以与对比度量学习相媲美。
并且指出,所使用的数据增强方法比选择的实际损失更为重要(Caron,Misra等,2020;Tian,Chen和Ganguli,2021)。在视觉和语言的背景下(第6.6节),CLIP (Radford,Kim等,2021)通过对比学习和“自然语言监督”在图像分类中实现了显著的泛化能力。他们使用了包含4亿个文本和图像对的数据集,任务是输入一张图像和32,768个随机抽取的文本片段,预测哪个文本片段真正与该图像配对。
有趣的是,最近发现仅在语义相似的输入之间强制相似性的表示学习也能很好地工作。这似乎违反直觉,因为如果没有对比学习中的负样本对,表示很容易通过预测任何输入的常数并最大化相似性而崩溃到平凡解。为了避免这种崩溃,通常会仔细关注网络设计。Bootstrap Your Own Latent(BYOL)(Grill,Strub等2020)表明,通过在线网络侧的动量编码器、额外的预测器MLP和目标网络侧的停止梯度操作,可以成功地从MoCo v2训练中移除负样本。SimSiam (Chen和He 2021)进一步证明,即使不需要动量编码器,仅使用停止梯度操作就足以让网络学习有意义的表示。虽然这两个系统都通过梯度更新联合训练预测器MLP和编码器,但最近的研究表明,可以直接使用输入在预测层之前的统计信息来设置预测器权重(Tian,Chen和Ganguli 2021)。Feicht- enhofer,Fan等人(2021)比较了这些无监督表示学习技术在多种视频理解任务上的表现,发现所学的空间时间表示能够很好地泛化到不同的任务。
对比学习和相关工作依赖于数据增强的组合(例如。
颜色抖动、随机裁剪等)来学习对这些变化不变的表示(陈和何2021)。另一种尝试是使用生成模型(陈、拉德福德等人2020),其中表示通过预测像素进行预训练,可以采用自回归(如GPT或其他语言模型)方式或去噪(如BERT、掩码自编码器)方式。生成模型有潜力弥合从视觉到自然语言处理领域的自监督学习差距,目前可扩展的预训练模型已占据主导地位。
自监督学习的最后一个变体是使用学生-教师模型,其中教师网络用于向学生网络提供训练样本。这类架构最初被称为模型压缩(Bucil、Caruana和Niculescu-Mizil 2006)和知识蒸馏(Hinton、Vinyals和Dean 2015),用于生成更小的模型。然而,当与额外数据和更
大容量网络结合时,它们也可以用来提高性能。Xie、Luong等人(2020)训练
在标注的ImageNet训练集上使用EfficientNet(Tan和Le 2019),然后利用该网络对额外的3亿未标注图像进行标注。随后,使用真实标签和伪标签图像来训练一个更高容量的“学生”模型,通过正则化(如丢弃)和数据增强来提高泛化能力。这一过程不断重复,以实现进一步的改进。
总的来说,自监督学习目前是深度学习中最令人兴奋的子领域之一,许多顶尖研究者认为它可能是实现更优深度学习的关键(LeCun和Bengio 2020)。为了进一步探索这些实现,VISSL提供了本节中描述的许多最先进自监督学习模型(带权重)的开源PyTorch实现。
虽然深度神经网络最初用于二维图像理解和处理应用,但现在它们也被广泛应用于三维数据,如医学图像和视频序列。我们还可以通过将一个时间帧的结果传递给下一个时间帧(甚至前后传递)来串联一系列深度网络。在本节中,我们将首先探讨三维卷积,然后讨论递归模型,这些模型可以向前或双向传播信息。我们还将研究生成模型,这些模型可以从语义或相关输入中合成全新的图像。
正如我们刚才提到的,计算机视觉中的深度神经网络最初用于处理常规的二维图像。然而,随着共享和分析的视频量增加,深度网络也被应用于视频理解,这在第6.5节中详细讨论。我们还看到这些技术在三维体积模型中的应用,例如从测距数据生成的占用地图(第13.5节)和体积医学图像(第6.4.1节)。
乍一看,我们已经研究过的卷积网络,如图5.33,5.34和5.39所示,似乎已经执行了三维卷积,因为它们的输入感受野是(x;y;c)中的三维框,其中c是(特征)通道维度。因此,原则上我们可以将滑动窗口(例如时间或高度上的)适配到二维网络中,然后就完成了。或者,我们可以使用类似分组卷积的方法。然而,

(Karpathy,Toderici等人,2014)©2014 IEEE。
一次性操作一个完整的3D体积,以及在所有内核中共享第三个维度的重量,以及在每一层都有多个输入和输出特征通道,这更加方便。
三维卷积最早的应用之一是在视频数据处理中分类人类动作(Kim、Lee和Yang 2007;Ji、Xu等2013;Baccouche、Mamalet等2011)。Karpathy、Toderici等人(2014)描述了多种融合时间信息的替代架构,如图5.52所示。单帧方法独立地对每一帧进行分类,完全依赖于该帧的内容。后期融合则从每帧生成特征,并进行片段级别的分类。早期融合将相邻的小帧组分入多通道的二维卷积神经网络。正如前面提到的,跨时间的交互不具备卷积方面的权重共享和时间平移不变性。最后,三维卷积神经网络(Ji、Xu等2013)(本图未显示)学习三维空间和时间不变性的核函数,这些核函数在时空窗口上运行并融合成最终得分。
Tran、Bourdev等人(2015)展示了如何通过在深度网络中结合非常简单的3×3×3卷积和池化来获得更好的性能。他们的C3D网络可以被视为“3D CNN的VGG”(Johnson 2020,第18讲)。Carreira和Zisserman(2017)将这种架构与包括通过并行路径分析像素和光流构建的双流模型进行了比较(图6.44b)。第6.5节关于视频理解讨论了这些及其他用于此类问题的架构,这些问题也受到了诸如递归神经网络(RNN)和LSTM等顺序模型的挑战,我们将在第5.5.2节中讨论。Johnson(2020)的第18讲关于视频理解的内容对所有这些视频理解架构进行了很好的综述。
除了视频处理之外,三维卷积神经网络还被应用于体积图像处理。两个从范围数据中建模和识别形状的例子,即3D ShapeNets(Wu,Song et al.2015)和VoxNet(Maturana和Scherer2015)

图5.53三维卷积网络应用于体积数据进行物体检测:
(a) 3D ShapeNets (Wu,Song等人,2015)©2015 IEEE;(b) VoxNet (Maturana和Scherer
2015)©2015 IEEE。
如图5.53所示,它们在医学图像分割中的应用实例
(Kamnitsas、Ferrante等人,2016;Kamnitsas、Ledig等人,2017)在第6.4.1节中进行了讨论。
我们在第13.5.1节中更详细地讨论了神经网络方法在三维建模中的应用
14.6.
与常规的二维卷积神经网络一样,三维卷积神经网络架构可以利用不同的空间和时间分辨率、步长以及通道深度,但它们可能非常耗费计算和内存。为了应对这一问题,Feichtenhofer、Fan等人(2019)开发了一种双流SlowFast架构,其中慢路径以较低的帧率运行,并与快速路径的特征结合,后者具有更高的时间采样率但通道数较少(图6.44c)。视频处理网络还可以通过使用通道分离卷积(Tran、Wang等人,2019)和神经架构搜索(Feichtenhofer,2020)来提高效率。多网格技术(附录A.5.3)也可以用于加速视频识别模型的训练(Wu、Girshick等人,2020)。

图5.54 Mesh R-CNN系统概述(Gkioxari、Malik和Johnson,2019)©
2019 IEEE。Mask R-CNN主干被两个3D形状推理分支增强。
体素分支预测每个检测到的对象的粗略形状,该形状在网格细化分支中通过一系列细化阶段进一步变形。
除了处理诸如体积密度、隐式距离函数和视频序列等三维网格数据外,神经网络还可以用于从单张图像推断出三维模型。一种方法是预测每个像素的深度,我们将在第12.8节中研究这一点。另一种方法是重建使用体积密度表示的完整三维模型(Choy,Xu等,2016),我们将在第13.5.1节和第14.6节中讨论。然而,一些更近期的实验表明,这些三维推理网络(Tatarchenko,Dosovitskiy和Brox,2017;Groueix,Fisher等,2018;Richter和Roth,2018)可能只是识别一般对象类别并进行少量拟合(Tatarchenko,Richter等,2019)。
三维点云的生成和处理也得到了广泛研究(Fan,Su,and Guibas2017;Qi,Su et al.2017;Wang,Sun et al.2019)。Guo,Wang et al.(2020)提供了一个全面的调查,回顾了该领域的200多篇出版物。
最后一种选择是从RGB-D (Wang,Zhang等,2018)或常规RGB (Gkioxari,Malik和Johnson,2019;Wickramasinghe,Fua和Knott,2021)图像中推断出三维三角化网格。图5.54展示了Mesh R-CNN系统的组成部分,该系统首先重建体积模型,然后检测三维物体的图像,并将每个图像转换为三角化网格。所需的基本操作和表示方法包括

图5.55深度循环神经网络(RNN)使用多个阶段处理序列数据,一个阶段的输出作为下一个阶段的输入。©Glassner(2018)。每个阶段都保持自己的状态并反向传播其梯度,尽管权重在所有阶段之间共享。(a)列显示了一个更紧凑的汇总图,而(b)列则显示了相应的展开版本。
虽然二维和三维卷积网络是处理图像和体积的良好选择,但有时我们希望处理一系列图像、音频信号或文本。利用先前已知信息的一个好方法是在某一时间点(例如视频帧)检测到的特征作为下一帧处理的输入。这种架构被称为递归神经网络(RNN),详细描述见古德费洛、本吉奥和库尔维尔(2016年,第10章)以及张、利普顿等人(2021年,第8章)。图5.55展示了此类架构的示意图。深层网络不仅将信息传递给后续层(最终输出),还将其部分信息作为下一层数据处理的输入。各层之间共享权重(类似于三维卷积核),反向传播需要计算所有展开单元(时间实例)的导数,并将这些导数相加以获得权重更新。
因为梯度可以在时间上向后传播很长的距离,因此可能会消失或爆炸(就像在残差网络出现之前的深度网络一样),所以也可以添加额外的门控单元来调节帧间的信息流动。这种架构被称为门控循环单元(GRU)和长短期记忆(LSTM)。
(Hochreiter和Schmidhuber1997;Zhang,Lipton等人2021,第9章)。
循环神经网络和长短期记忆网络常用于视频处理,因为它们能够融合随时间变化的信息并建模时间依赖关系(Baccouche,Mamalet等2011;Donahue,Hendricks等2015;Ng,Hausknecht等2015;Srivastava,Mansimov,和Salakhudinov 2015;Ballas,Yao等2016),以及语言模型、图像描述和视觉问答。我们将在第6.5节和第6.6节中详细讨论这些主题。它们还偶尔被用于在立体视觉中合并多视图信息(Yao,Luo等2019;Riegler和Koltun 2020a),以及以完全可微(因此可训练)的方式模拟迭代流算法(Hur和Roth 2019;Teed和Deng 2020b)。
为了在时间上传播信息,RNN、GRU和LSTM需要在传递的时间步之间隐藏状态中编码所有可能有用的先前信息。在某些情况下,序列建模网络需要回溯(或甚至向前)更远的时间。这种能力通常被称为注意力机制,在张、利普顿等人(2021年,第10章)、约翰逊(2020年,第12讲)以及关于变压器的第5.5.3节中有详细描述。简而言之,具有注意力机制的网络存储键值列表,可以通过查询来探测这些列表,根据查询与每个键之间的对齐情况返回加权混合值。在这个意义上,它们类似于我们在第4.1.1节中研究的核回归(4.12–4.14),不同之处在于查询和键在通过softmax确定混合权重之前会进行乘法运算(并赋予适当的权重)。
注意力机制可以用于回顾先前时间实例中的隐藏状态(这被称为自注意力),也可以用于查看图像的不同部分(视觉注意力,如图6.46所示)。我们将在第6.6节关于视觉和语言的部分中详细讨论这些主题。在识别或生成序列时,例如句子中的单词,注意力模块通常与顺序模型如RNN或LSTM协同工作。然而,最近的研究已经使得可以在一个并行步骤中将注意力应用于整个输入序列成为可能,具体描述见第5.5.3节关于变压器的内容。
本节中的简要描述仅略窥深度序列建模这一广泛主题的皮毛,该主题通常在深度学习课程中通过几讲(例如,John- son2020,第12-13讲)和深度学习教科书中的若干章节(Zhang,Lipton等2021,第8-10章)进行详细阐述。感兴趣的读者可参考这些资料获取更详尽的信息。
变压器是一种新颖的架构,它添加了注意力机制(我们将其去-
(见下文)是Vaswani、Shazeer等人(2017年)首次引入的深度神经网络
在神经机器翻译的背景下,任务是将文本从一种语言翻译成另一种语言(Mikolov,Sutskever等,2013)。与处理输入标记逐个的循环神经网络及其变体(第5.5.2节)不同,变压器可以一次性处理整个输入序列。自首次引入以来,变压器成为自然语言处理(NLP)中许多任务的主要范式,使得BERT (Devlin,Chang等,2018)、RoBERTa (Liu,Ott等,2019)和GPT-3 (Brown,Mann等,2020)等模型取得了令人印象深刻的结果。随后,变压器在处理自然语言组件以及许多视觉和语言任务的后续层时开始取得成功(第6.6节)。最近,它们在纯计算机视觉任务中也获得了关注,在多个流行基准测试中甚至超过了卷积神经网络。
将变压器应用于计算机视觉的动机与应用于自然语言处理不同。RNN由于顺序处理输入而存在问题,而卷积则没有这个问题,因为其操作本身是并行的。相反,卷积的问题在于其归纳偏见,即编码到卷积模型中的默认假设。
卷积操作假设邻近像素比远距离像素更重要。只有当多个卷积层堆叠在一起时,感受野才会足够大以关注整个图像(Araujo,Norris,和Sim 2019),除非网络配备了非局部操作(Wang,Girshick等2018),类似于某些图像去噪算法中使用的操作(Buades,Coll,和Morel 2005a)。正如我们在本章中所见,卷积的空间局部性偏见在计算机视觉的许多方面取得了显著成功。但随着数据集、模型和计算能力呈指数级增长,这些归纳偏见可能成为阻碍进一步发展的因素。54
变压器的基本组件是自注意力机制,它通过在网络中给定层的每个单元激活应用注意力来构建。55注意力通常用编程语言和数据库中的关联映射或字典的概念作比喻。给定一组键值对{(ki;vi)}和查询q,字典会返回与查询完全匹配的键ki对应的值vi。在神经网络中,键和查询值是实数值向量(例如,激活的线性投影),因此相应的操作返回一个加权值之和,其中权重取决于查询与键集之间的两两距离。这基本上与散点数据插值相同,我们曾在研究过。

图5.56自注意力计算图用于计算单个输出向量x,由Matt Deitke提供,改编自Vaswani、Huang
和Manning(2019)。请注意,完整的自注意力操作还为x、x和x4分别计算了输入到查询(此处为x2)在x1、x3和x4之间的输出。对于
matmul V、matmulK和matmulQ,都有一个权重矩阵,在每次调用时都会被重用。
第4.1.1节,如张、利普顿等人(2021年,第10.2节)所指出。然而,神经网络中的注意力机制通常不使用径向距离(4.14),而是采用缩放点积注意力机制(瓦斯瓦尼、沙泽尔等人2017年;张、利普顿等人2021年,第10.3.3节),该机制涉及查询向量和键向量之间的点积,通过这些嵌入向量的维度D的平方根进行缩放,然后应用(5.5)中的softmax函数,即,
(5.77)
其中,K和V分别是由键向量和值向量组成的行堆叠矩阵,y是注意力算子的输出。57
给定一组输入向量{x0;x1;...;xN - 1 },自注意力操作产生一组输出向量{x;x;...;x - 1 }。图5.56显示了N =
4的
情况,其中
自注意力计算图用于获得单个输出向量x。如图所示,自注意力使用三个学习
到的权重矩阵Wq、Wk和Wv,它们决定了
qi = Wqxi;ki = Wkxi;和vi = Wv xi (5.78)
每个注意力块中输入的单位查询、键和值向量。加权和为
然后,值可选地通过多层感知器(MLP)来产生x。
与全连接层或卷积层相比,自注意力机制根据所有输入向量{x0;x1;...;xN - 1 }计算每个输出(例如,xi)。因此,它常被比作全连接层,但权重不是固定不变的,而是根据输入即时调整(Khan,Naseer等,2021)。与卷积相比,自注意力机制能够从一开始就关注输入的每一个部分,而不是局限于输入的局部区域,这可能有助于引入图6.8所示对象所需的上下文信息。
有几个组件与自注意力机制结合,生成一个转换器块,如瓦斯瓦尼、沙泽尔等人(2017)所述。完整的变压器包括编码器和解码器两个部分,尽管两者共享许多相同的组件。在许多应用中,可以使用编码器而不使用解码器(德夫林、张等人,2018;多索维茨基、贝耶等人,2021),反之亦然(拉扎维、范登奥德和文亚尔,2019)。
图5.57右侧显示了变压器编码器模块的一个示例。对于编码器和解码器:
•我们可以不建模集合到集合的操作,而是通过向每个输入向量添加位置编码来建模序列到序列的操作(Gehring,Auli等,2017)。位置编码通常由一组时间偏移的正弦波组成,从中可以解码出位置信息。(这种位置编码最近也被添加到隐式神经形状表示中,我们将在第13.5.1节和第14.6节中研究。)
•代替对输入应用单一的自注意力操作,通常会将多个自注意力操作组合在一起,使用不同的学习权重矩阵来构建不同的键、值和查询,形成多头自注意力(Vaswani,Shazeer等,2017)。每个头的结果随后被连接在一起,然后通过一个MLP。
•然后将层归一化(Ba、Kiros和Hinton2016)应用于MLP的输出。然后,每个向量可以独立地通过另一个具有共享权重的MLP,然后再应用层归一化。
在多头注意力机制和最终MLP之后采用残余连接(He,Zhang等人,2016a)。
训练过程中,解码器最大的不同在于自注意力机制中的一些输入向量可能会被屏蔽,这有助于支持自回归预测任务中的并行训练。关于变压器架构的详细说明和实现,请参见Vaswani、Shazeer等人(2017)以及附加阅读材料(第5.6节)。
将变压器应用于图像领域的一个关键挑战与图像输入的大小有关(Vaswani,Shazeer等,2017)。设N表示输入长度,D表示每个输入条目的维度数,K表示卷积(侧)核的大小。自注意力机制所需的浮点运算次数(FLOPs)约为O(N^2D),而卷积操作的FLOPs则约为O(ND^2K^2)。例如,对于一个缩放至224×224×3的ImageNet图像,如果每个像素独立处理,则N = 224×224 = 50176,D = 3。在这里,卷积比自注意力机制显著更高效。相比之下,像神经机器翻译这样的应用可能只有N表示句子中的单词数,D表示每个词嵌入的维度(Mikolov,Sutskever等,2013),这使得自注意力机制更加高效。
图像变换器(Parmar、Vaswani等,2018)是首次尝试将完整的变压器模型应用于图像领域,许多介绍变压器的作者也参与了这一研究。它使用了编码器和解码器,试图构建一个自回归生成模型,该模型能够根据输入像素序列和所有先前预测的像素来预测下一个像素。(王、Girshick等(2018)关于非局部网络的早期工作也借鉴了变压器的思想,但采用了更简单的注意力块和完全二维的设置。)每个输入向量对应一个像素,这最终限制了它们生成的小图像尺寸(即32×32),因为自注意力机制的二次成本过高。
多沃维茨基、贝耶等人(2021)取得了一项突破,使得变压器能够处理更大的图像。图5.57展示了名为视觉变压器(ViT)的模型图。对于图像识别任务,他们没有将每个像素视为变压器的独立输入向量,而是将一张224×224的图像分割成196个不同的16×16网格图像块。每个块被展平后,通过一个共享嵌入矩阵,这相当于一个步长为16×16的卷积,结果与位置编码向量结合后传递给变压器。早期的工作

图5.57来自(Dosovitskiy,Beyer的视觉变换器(ViT)模型 etal2021)将图像分解为一个16×16的补丁网格。每个补丁随后被展平,通过共享嵌入矩阵,并与位置编码向量结合。这些输入随后多次通过变压器编码器(右侧),然后预测图像的类别。
Cordonnier、Loukas和Jaggi(2019)引入了类似的补丁方法,但规模较小,为2×2补丁。
ViT只有在使用超过一亿张来自JFT-300M的训练图像时(Kolesnikov,Beyer等,2020),才能超越其卷积基线BiT(Sun,Shrivastava等,2017)。仅使用ImageNet,或从JPT-300中随机选取一千万或三千万张训练样本时,ViT模型的表现通常远逊于BiT基线。他们的结果表明,在低数据量领域,卷积中固有的归纳偏置通常非常有用。但是,当数据量增加几个数量级时,变压器模型可能会发现更好的表示方法,而这些方法是卷积神经网络无法实现的。
一些研究还尝试将卷积的归纳偏置与变压器结合(Srinivas,Lin等,2021;Wu,Xiao等,2021;Lu,Batra等,2019;Yuan,Guo等,2021)。一个具有影响力的网络示例是DETR (Carion,Massa等,2020),该网络应用于目标检测任务。它首先使用ResNet主干处理图像,输出结果传递给变压器编码器-解码器架构。他们发现加入变压器可以提高检测大物体的能力,这被认为是因为变压器能够全局地推理输入编码向量之间的对应关系。
变压器在计算机视觉领域的应用和实用性仍在广泛研究中。然而,它们已经在计算机视觉领域取得了令人印象深刻的表现。
广泛的任务,新论文迅速发表。59更多值得注意的应用包括图像分类(刘、林等2021;图沃龙、科尔德等2020),物体检测(戴、蔡等2020;刘、林等2021),图像预训练(陈、拉德福德等2020),语义分割(郑、陆等2020),姿态识别(李、王等2021),超分辨率(曾、傅、曹2020),色彩化(库马尔、魏森博恩、卡尔布伦纳2021),生成建模(江、张、王2021;哈德森和齐特尼克2021),以及视频分类(阿纳布、德赫加尼等2021;范、熊等2021;李、张等2021)。近期研究还成功地将ViT的补丁嵌入扩展到纯MLP视觉架构(托尔斯蒂欣、豪尔比等2021;刘、戴等2021;图沃龙、博亚诺夫斯基等2021)。视觉和语言应用详见第6.6节。
在本章中,我提到过诸如逻辑回归、支持向量机、随机树和前馈深度神经网络等机器学习算法都是判别系统的一个例子,这些系统从未形成它们试图估计的数量的显式生成模型(Bishop 2006,第1.5节;Murphy 2012,第8.6节)。除了这两本教科书中讨论的生成模型的潜在优势外,Goodfellow(2016)和Kingma与Welling(2019)还列出了其他一些优势,例如能够可视化我们对未知变量的假设、使用缺失或不完全标记的数据进行训练,以及生成多个替代结果的能力。
在计算机图形学中,有时也称为图像合成(与我们在计算机视觉中进行的图像理解和图像分析相对),能够轻松生成逼真的随机图像和模型一直是必不可少的工具。这类算法的例子包括纹理合成和风格迁移,我们将在第10.5节中详细研究,还有分形地形(Fournier、Fussel和Carpenter 1982)以及树木生成(Prusinkiewicz和Lindenmayer 1996)。图5.60和10.58展示了深度神经网络用于生成这些新颖图像的例子,通常是在用户控制下进行的。相关技术也被应用于新兴的神经渲染领域,我们将在第14.6节中讨论。
我们如何解锁深度神经网络展现的强大能力,以捕捉语义,从而可视化样本图像并生成新的图像?一种方法是使用第5.4.5节介绍的可视化技术。但正如图5.49所示,虽然这些技术可以让我们了解单个单元,却无法创建
非常逼真的图像。
另一种方法可能是构建一个解码器网络,以撤销原始(编码器)网络执行的分类。这种“瓶颈”架构被广泛使用,如图5.37a所示,用于从图像中提取每个像素的语义标签。我们能否利用类似的想法生成逼真的图像?
变分自编码器
一种网络将图像编码成小而紧凑的代码,然后尝试将其解码回相同的图像,这种网络被称为自编码器。这些紧凑的代码通常表示为向量,常称为潜在向量,以强调它是隐藏且未知的。自编码器在神经网络中的应用历史悠久,甚至早于当今的前馈网络(Kingma和Welling 2019)。曾经认为这可能是预训练网络的好方法,但我们在第5.4.7节研究的更具挑战性的代理任务已被证明更为有效。
在高层次上,为了在一个图像数据集上训练自动编码器,我们可以使用一个无监督的目标函数,该函数试图让解码器的输出图像与输入到编码器的训练图像相匹配。为了生成新的图像,我们可以随机抽取一个潜在向量,并希望从这个向量中,解码器能够生成一个新的图像,使其看起来像是来自我们数据集中训练图像分布的一部分。
使用自动编码器时,每个输入到其潜在向量之间存在确定性的、一对一的映射。因此,生成的潜在向量数量与输入数据点的数量完全匹配。如果编码器的目标是生成易于解码的潜在向量,一种可能的解决方案是每个潜在向量都与其他所有潜在向量相距甚远。在这种情况下,解码器可以过度拟合它见过的所有潜在向量,因为这些向量都是独特的,几乎没有重叠。然而,我们的目标是随机生成可以传递给解码器以生成逼真图像的潜在向量,因此我们希望潜在空间既能够充分探索,又能编码一些意义,例如相邻向量在语义上相似。Ghosh、Sajjadi等人(2019)提出了一种潜在解决方案,即向潜在向量中注入噪声,并通过实验证明这种方法效果很好。
自动编码器的另一个扩展是变分自编码器(VAE)(Kingma和Welling 2013;Rezende、Mohamed和Wierstra 2014;Kingma和Welling 2019)。它不是为每个输入生成一个单一的潜在向量,而是生成定义所选潜在向量分布的均值和协方差。然后可以从该分布中采样出一个潜在向量,该向量被传递给解码器。为了避免协方差矩阵变成零矩阵,使得采样过程变得确定性,目标函数通常包含一个正则化项来惩罚分布过于集中。

图5.58 VQ-VAE模型。左侧,ze (x)表示编码器的输出,上方的嵌入空间表示包含K个嵌入向量的码本,q(z j x)表示将编码器输出中的每个空间(即通道)向量替换为其在码本中最接近的向量的过程。右侧,我们看到ze (x)向量(绿色)可能被四舍五入到e2,而编码器网络中的梯度(红色)在反向传播过程中可能会将该向量从e2推离。©van den Oord,Vinyals和Kavukcuoglu(2017)
来自一些选定的(例如高斯)分布。由于其概率性质,VAE可以比自动编码器更好地探索可能的潜在向量空间,使解码器更难过度拟合训练数据。
受到自然语言离散性和图像通常可以用语言描述的启发(第6.6节),范登奥德、维尼亚尔斯和卡武库奥卢(2017)提出的向量量化VAE(VQ-VAE)采用了一种用分类变量建模潜在空间的方法。图5.58展示了VQ-VAE架构的概要。编码器和解码器的工作方式与普通VAE相同,其中编码器从输入中预测某个潜在表示,而解码器则从潜在表示生成图像。然而,与普通VAE不同的是,VQ-VAE用离散向量集(称为代码本)中的最近向量替换了预测潜在表示的每个空间维度。离散化的潜在表示随后传递给解码器。代码本中的向量与VAE的编码器和解码器同时训练。在这里,代码本向量被优化以更接近由编码器输出的空间向量。
尽管VQ-VAE使用了一个离散的向量码本,但它能够表示的图像数量仍然极其庞大。在他们的一些图像实验中,将码本的大小设置为K = 512个向量,并将潜在变量的大小设置为z = 32×32×1。这样,他们可以表示512³·32·1个可能的图像。
与通常假设高斯潜在分布的VAE相比,潜在
VQ-VAE的分布并不那么明确,因此需要训练一个独立的生成模型来采样潜在变量z。该模型是在训练数据中使用已训练的VQ-VAE编码器输出的最终潜在变量进行训练的。对于图像而言,z中的条目通常具有空间依赖性,例如,一个对象可能被编码在许多相邻的条目上。通过从离散向量代码集中选择条目,我们可以使用PixelCNN (van den Oord,Kalchbrenner等,2016)根据先前采样的邻近条目自回归地采样潜在变量的新条目。PixelCNN还可以有条件地训练,这使得能够根据特定的图像类别或特征采样潜在变量。
VQ-VAE模型的后续版本,名为VQ-VAE-2 (Razavi、van den Oord和Vinyals 2019),采用两级解码图像的方法,通过使用小和大的潜在向量,能够获得更高保真的重建和生成图像。第6.6节讨论了Dall·E(Ramesh、Pavlov等2021),该模型将VQ-VAE-2应用于文本到图像的生成,并取得了显著成果。
另一种图像合成的可能性是利用预训练网络计算出的多分辨率特征来匹配给定纹理或风格图像的统计特性,如图10.57所示。虽然这类网络对于匹配特定艺术家的风格和照片的高层次内容(布局)非常有用,但它们不足以生成完全逼真的图像。
为了生成真正逼真的合成图像,我们希望确定一张图像是真实的(逼真)还是假的。如果存在这样的损失函数,我们可以用它来训练网络生成合成图像。但是,由于这种损失函数难以手动编写,为什么不训练一个单独的神经网络来扮演批评者的角色呢?这是由古德费洛、普热-阿巴迪等人(2014)引入的生成对抗网络的主要见解。在他们的系统中,生成器网络G的输出被输入到另一个判别器网络D中,其任务是区分“假”的合成图像和真实图像,如图5.59a所示。生成器的目标是创建能够“欺骗”判别器将其接受为真实的图像,而判别器的目标则是抓住“伪造者”的行为。两个网络同时进行联合训练,使用一系列损失函数来鼓励每个网络完成其任务。联合损失函数可以表示为
EGAN(wG,wD)= log D(xn)+ log(1 - D(G(zn))), (5.79)
其中{xn }是真实世界的训练图像,{zn }是随机向量

图5.59 Pan、Yu的生成对抗网络(GAN)架构 等(2019)©2019 IEEE. (a)在常规的生成对抗网络中,随机的“潜在”噪声向量z被输入到生成器网络G中,该网络生成合成的“假”图像x,= G(z)。判别器D的任务是区分这些假图像与真实样本x。(b)在条件生成对抗网络(cGAN)中,网络会在训练过程中遍历我们希望生成的所有类别。生成器G以类别ID c和随机噪声向量z作为输入,且
判别器D也获得类别ID,并需要确定其输入是否是给定类别的真实成员。(c)InfoGAN中的判别器无法访问类别ID,但必须从给定的样本中推断出来。
通过生成器G产生合成图像xn,{wG,wD }是生成器和判别器中的权重(参数)。
我们不是最小化这一损失,而是调整生成器的权重以最小化第二项(它们不影响第一项),同时调整判别器的权重以最大化这两项,即最小化判别器的误差。这个过程通常被称为极小极大博弈。关于该公式及其优化方法的更多细节,可以在古德费洛、普热-阿巴迪等人(2014)的原始论文中找到,也可以在深度学习教材(张、利普顿等人2021,第17章)、讲座(约翰逊2020,第20讲)、教程(古德费洛、伊索拉等人2018)和综述文章(克雷斯韦尔、怀特等人2018;潘、余等人2019)中找到。
古德费洛、普热-阿巴迪等人(2014)的原始论文使用了一个小型的全连接网络来展示基本思想,因此只能生成32×32的图像,如MNIST数字和低分辨率人脸。拉德福德、梅茨和钦塔拉(2015)引入的深度卷积生成对抗网络(DCGAN)使用图5.37a所示的反卷积网络的后半部分,将随机潜在向量z映射到任意大小的图像,因此可以生成更广泛种类的输出,而LAPGAN则使用
一个对抗网络的拉普拉斯金字塔(Denton,Chintala等人,2015)。在不同的潜在向量之间混合(或在某些方向上扰动它们)生成中间合成图像。
生成对抗网络(GAN)和深度判别生成对抗网络(DCGAN)可以训练生成给定类别的新样本,但使用同一训练网络从不同类别生成样本更为有用。由米尔扎和奥斯因德罗(2014)提出的条件生成对抗网络(cGAN),通过向生成器输入一个类别向量来实现这一点,该向量不仅影响生成器的输出,还影响判别器,如图5.59b所示。此外,还可以通过增加一个互信息项,让判别器预测与类别向量相关的类别,如图5.59c所示(陈、段等人,2016)。这使得生成的信息对抗网络能够学习解耦表示,例如MNIST中的数字形状和书写风格,或姿态和光照。
虽然生成随机图像可以有许多有用的图形应用,例如生成纹理、填充孔洞和美化照片,如第10.5节所述,但当这些操作可以在人的艺术控制下完成时,其价值更加凸显(Lee,Zitnick,和Cohen 2011)。由Zhu和Kra开发的iGAN交互式图像编辑系统... ...henbuhl等人(2016)通过使用生成对抗网络学习一个逼真的图像流形,然后限制用户编辑(甚至草图),以产生位于该流形上的图像。
这种方法被Isola、Zhu等人(2017)推广到所有其他图像到图像的转换任务,如图5.60a所示。在他们的pix2pix系统中,输入可以是草图或语义标签,这些图像被送入一个修改后的U-Net,将其转换为具有不同语义意义或风格的图像(例如照片或道路地图)。当输入是语义标签图,输出是逼真的图像时,这一过程通常被称为语义图像合成。翻译网络通过条件GAN进行训练,该网络在训练时使用来自两个域的配对图像,并让判别器判断合成(翻译)的图像与输入图像是否为真实或虚假对。回到图5.59b,类别c现在是一个完整的图像,它被送入G和判别器D,以及其配对或合成的输出。判别器不再对整个图像做出决定,而是查看重叠的块,并逐块地做出决策,这需要更少的参数,并提供更多的训练数据和更有区分性的反馈。在他们的实现中,没有随机向量z;相反,在训练和“测试”(翻译)时间都使用了dropout,这相当于在网络的不同层级注入噪声。
在许多情况下,配对的图像不可用,例如,当你有来自不同地点的绘画和照片集合,或者动物的两张不同的图片

图5.60图像到图像的转换。(a)给定配对的训练图像,原始的pix2pix系统学会了如何将素描转化为照片、语义地图转化为图像以及其他像素重映射任务(Isola,Zhu等2017)©2017 IEEE。(b) CycleGAN不需要配对的训练图像,只需要来自不同来源的集合,例如绘画和照片或马和斑马(Zhu,Park等2017)©2017 IEEE。
如图5.60b所示,在这种情况下,可以使用循环一致性对抗网络(Cycle- GAN)来要求两个域之间的映射鼓励同一性,同时确保生成的图像在感知上与训练图像相似(Zhu,Park等,2017)。DualGAN(Yi,Zhang等,2017)和DiscoGAN(Kim,Cha等,2017)采用了类似的思想。Zhu,Zhang等(2017)的BicycleGAN系统也使用了类似的转换周期思想,以促进编码的潜在向量对应于输出的不同模式,从而提高可解释性和控制力。
自GAN论文发表以来,扩展、应用和后续论文的数量呈爆炸式增长。GAN动物园网站61列出了2014年至2018年中期发布的500多篇GAN论文,此后该网站停止更新。大量

图5.61语义图像金字塔可用于选择在编辑图像时修改深度网络中的哪个语义级别(Shocher,Gandelsman (et al.2020)©2020 IEEE。
每年都有论文出现在视觉、机器学习和图形会议上。
自2017年以来的一些重要论文包括:Wasserstein GANs(Arjovsky、Chintala和Bottou 2017)、Progressive GANs(Karras、Aila等2018)、UNIT(Liu、Breuel和Kautz 2017)和MUNIT(Huang、Liu等2018)、谱归一化(Miyato、Kataoka等2018)、SAGAN (Zhang、Goodfellow等2019)、BigGAN (Brock、Donahue和Simonyan 2019)、StarGAN(Choi、Choi等2018)和StyleGAN (Karras、Laine和Aila 2019),以及后续论文(Choi、Uh等2020;Karras、Laine等2020;Viazovetsky、Ivashkin和Kashin 2020)、SPADE (Park、Liu等2019)、GANSpace(Ha...o...nen、rk Hertzmann等2020)和VQGAN (Esser、Rombach和Ommer 2020)。您可以在约翰逊的讲座(2020,第20讲)、古德费洛、Isola等人的教程(2018)以及克雷斯韦尔、怀特等人的综述文章(2018)、潘、余等人的综述文章(2019)和特瓦里、弗里德等人的综述文章(2020)中找到更多详细解释和参考文献。
总之,生成对抗网络及其众多扩展仍然是一个极其活跃且有用的研究领域,应用包括图像超分辨率(第10.3节)、逼真图像合成(第10.5.3节)、图像到图像转换以及交互式图像编辑。最近两个此类应用的例子是Shocher、Gandelsman等人(2020年)提出的图像生成语义金字塔,其中语义操作级别可以控制(从小纹理变化到高级布局变化),如图5.61所示,以及Swapping Autoencoder。
机器学习和深度学习是丰富而广泛的主题,它们理应拥有自己的课程来掌握。幸运的是,有大量的优秀的教科书和在线课程可供学习这些内容。
我最喜爱的机器学习书籍是毕晓普(2006)的那本,因为它提供了广泛的贝叶斯风格的处理方法和出色的图表,这些图表我在本书中也重新使用了。格拉斯纳(2018,2021)的书则以更加温和的方式介绍了经典机器学习和深度学习,以及我在本书中引用的额外图表。另外两本广泛使用的机器学习教科书是哈斯蒂、蒂布沙里尼和弗里德曼(2009)和墨菲(2012)。德森罗思、费萨尔和翁(2020)提供了一本关于机器学习数学的精炼处理,包括线性和矩阵代数、概率论、模型拟合、回归、主成分分析和支持向量机,其内容比我在这本书中提供的简要概述更为深入。由胡特、科特霍夫和范肖伦(2019)编辑的《自动化机器学习》一书综述了设计和优化机器学习算法的自动化技术。
对于深度学习,古德费洛、本吉奥和库尔维尔(2016)首次提供了全面的论述,但最近并未修订。格拉斯纳(2018,2021)则以大量图表和无方程的形式,为深度学习提供了精彩的介绍。我甚至推荐给有经验的从业者,因为它有助于培养和巩固关于学习如何工作的直觉。最新的深度学习参考书是张、利普顿等人(2021)编写的《深入浅出的深度学习》在线教材,书中穿插了互动的Python笔记本,以及相关的课程(斯莫拉和李2019)。一些深度学习入门课程使用查尼亚克(2019)的教材。
拉瓦特和王(2017)提供了一篇关于深度学习的精彩综述文章,包括早期和后期神经网络的历史,以及对许多深度学习组件的深入讨论,如池化、激活函数、损失函数、正则化和优化。与深度学习进展相关的其他综述还包括塞兹、陈等人(2017)、埃尔斯肯、梅岑和胡特(2019)、顾、王等人(2018)和乔杜里、米什拉等人(2020)。塞伊诺夫斯基(2018)提供了神经网络早期历史的详细回顾。
约翰逊(2020)的《计算机视觉深度学习》课程幻灯片是极佳的参考材料,也是学习该主题的绝佳途径,不仅因为其信息的深度,还因为演示内容的时效性。这些幻灯片基于斯坦福大学的CS231n课程(李、约翰逊和杨2019),该课程同样是一个非常及时的资源。其他包含幻灯片和/或视频讲座的深度学习课程包括格罗斯和巴(2019)、麦克阿莱斯特(2020)、莱尔-泰克斯和Nießner(2020)、莱尔-泰克斯和Nießner(2021)以及盖格(2021)。
对于变压器,Bloem(2019)提供了一个很好的入门教程,从零开始在PyTorch中实现标准的变压器编码器和解码器块。关于变压器在计算机视觉中的应用,更全面的综述包括Khan、Naseer等人(2021)和Han、Wang等人(2020)。Tay、Dehghani等人(2020)概述了许多尝试减少自注意力机制二次成本的方法。Wightman(2021)提供了一个精彩的PyTorch计算机视觉变压器实现集合,包含预训练权重和详尽的文档。此外,介绍变压器的课程讲座包括Johnson (2020,第13讲)、Vaswani、Huang和Manning (2019,第14讲)以及LeCun和Canziani (2020,第12周)。
对于生成对抗网络(GAN),张、利普顿等人(2021年,第17章)的新深度学习教科书、约翰逊(2020年,第20讲)的讲座、古德费洛、伊索拉等人(2018年)的教程以及克雷斯韦尔、怀特等人(2018年)、潘、余等人(2019年)和特瓦里、弗里德等人(2020年)的综述文章都是很好的资料来源。关于最新视觉识别技术的综述,国际计算机视觉会议(Xie、吉什里克等人2019年)、计算机视觉与模式识别学会(Girshick、基里洛夫等人2020年)和欧洲计算机视觉协会(Xie、吉什里克等人2020年)的教程是极佳的最新资料来源。
例5.1:反向传播和权重更新。在简单的神经网络中实现前向激活、后向梯度和误差传播以及权重更新步骤。你可以在2020年威斯康星大学计算机科学与工程系576课程的HW3中找到此类代码示例,或者参考McAllester(2020)开发并在Geiger(2021)中使用的教育框架(EDF)。
例5.2:LeNet。下载、训练并测试一个简单的“LeNet”(LeCun,Bottou等,1998)卷积神经网络,数据集可以是CIFAR-10(Krizhevsky,2009)或Fashion MNIST (Xiao,Rasul,和Vollgraf,2017)。你可以在网上找到许多这样的代码,包括2020年华盛顿大学计算机科学与工程576课程的HW4或者PyTorch初学者教程中的神经网络部分。63
修改网络以消除非线性。性能如何变化?通过增加通道数、层数或卷积大小,能否提高原始网络的性能?在修改网络时,训练和测试的准确性是朝着相同的方向还是不同的方向发展?
例5.3:深度学习教科书。Glassner(2018,第15、23和24章)的《深度学习:从基础到实践》和Zhang的《深入深度学习》



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








