11.1几何内禀校准 685
11.1.1消失点 687
11.1.2应用:单视图计量 688
11.1.3旋转运动 689
11.1.4径向畸变 691
11.2姿态估计 693
11.2.1线性算法 693
11.2.2迭代非线性算法 695
11.2.3应用:位置识别 698
11.2.4三角测量 701
11.3从运动中获得的双帧结构 703
11.3.18、7和5点算法 703
11.3.2特殊动线和结构 708
11.3.3投影(未校准)重建 710
11.3.4自校准 712
11.3.5应用:查看变形 714
11.4从运动中提取多帧结构 715
11.4.1因式分解 715
11.4.2捆绑调整 717
11.4.3利用稀疏性 719
11.4.4应用:匹配移动 723
11.4.5不确定性和模糊性 723
11.4.6应用:从网络照片中重建 725
11.4.7从运动中获取全局结构 728
11.4.8结构和运动受限 731
11.5同步定位与建图(SLAM) 734
11.5.1应用:自主导航 737
11.5.2应用:智能手机增强现实 739

图11.1运动结构示例:(a)二维校准目标(张2000)©2000 IEEE;(b)单视图测量(克里米尼西、里德和齐瑟曼2000)©2000斯普林格。(c–d)线匹配(施密德和齐瑟曼1997)©1997 IEEE;(e–g)特拉法加广场、中国长城和布拉格老城广场的三维重建(斯纳维利、塞茨和泽利斯基2006)©2006 ACM;(h)智能手机增强现实显示实时深度遮挡效果(瓦伦丁、科德尔等人2018)©2018 ACM。
从图像重建三维模型自计算机视觉诞生以来一直是其核心主题之一(图1.7)。事实上,当时人们认为构建三维模型是场景理解和识别的前提条件(Marr1982),尽管近几十年的工作已经证明了这一点。然而,三维建模在虚拟旅游(第11.4.6节)、自主导航(第11.5.1节)和增强现实(第11.5.2节)等应用中也被证明具有极大的价值。
在前三个章节中,我们专注于建立二维图像之间对应关系的技术,并将其应用于图像拼接、视频增强和计算摄影等多种场景。本章我们将探讨如何利用这些对应关系构建场景的稀疏三维模型,并根据这些模型重新定位相机。尽管这一过程通常涉及同时估计三维几何(结构)和相机姿态(运动),但出于历史原因,它常被称为运动从结构(Ullman1979)。
射影几何和运动结构这两个主题极其丰富,已经有一些优秀的教科书和综述文章对此进行了阐述(Faugeras和Luong 2001;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010;Ma、Soatto等2012)。本章跳过了这些书中许多更丰富的材料,例如三焦张量和用于完全自校准的代数技术,而是集中讨论了我们在大规模基于图像的重建问题中发现有用的基理论(Snavely、Seitz和Szeliski 2006)。
我们在第11.1节开始本章,回顾常用的相机内参校准技术,例如我们在第2.1.4–2.1.5节中介绍的焦距和径向畸变参数。接下来,我们讨论如何从三维到二维点对应关系估计相机的外参姿态(第11.2节),以及如何通过三角测量一组二维对应关系来估计一个点的三维位置。然后,我们探讨两帧结构从运动问题(第11.3节),该问题涉及确定两个相机之间的极线几何关系,也可以利用自校准恢复某些关于相机内参的信息(第11.3.4节)。第11.4.1节研究了使用正交投影模型近似同时估计大量点轨迹的结构和运动的方法。随后,我们发展了一种更通用且有用的结构从运动方法,即所有相机和三维结构参数的同时束调整(第11.4.2节)。我们还探讨了场景中存在更高层次结构,如直线和平面时出现的特殊情况(第11.4.8节)。本章的最后一部分(第11.5节),我们研究了实时系统中的同时定位与建图(SLAM),该系统在移动过程中重建三维世界模型,并可应用于视觉
正如我们在下一节(公式(11.14–11.15))中讨论的,相机内部(内在)校准参数的计算可以与相机相对于已知校准目标的姿态估计同时进行。这确实是摄影测量学(Slama1980)和计算机视觉(Tsai1987)领域中常用的“经典”相机校准方法。在本节中,我们将探讨一些更简单的替代方案,这些方案可能不需要完全解决非线性回归问题,使用不同的校准目标,并估计相机光学的非线性部分,如径向畸变。在某些应用中,可以利用与JPEG图像关联的EXIF标签来粗略估计相机的焦距,从而初始化迭代估计算法;但这种方法应谨慎使用,因为结果往往不准确。
校准模式
使用校准图案或一组标记是估计相机内参的一种较为可靠的方法。在摄影测量中,通常会将相机放置在一个大范围内,观察远处的校准目标,这些目标的确切位置已通过测量设备预先计算(Slama 1980;Atkinson 1996;Kraus 1997)。在这种情况下,姿态的平移分量变得无关紧要,只需恢复相机的旋转和内参参数。
如果需要使用较小的校准装置,例如用于室内机器人应用或携带自身校准目标的移动机器人,最好让校准对象尽可能覆盖工作空间的大部分(图11.2a),因为平面目标往往无法准确预测远离平面的姿态组件。判断校准是否成功的一个好方法是估计参数的协方差(第8.1.4节),然后将工作空间中不同点的3D点投影到图像中,以估计它们的2D位置不确定性。
如果没有校准图案,也可以同时进行结构和姿态恢复的校准(第11.1.3节和第11.4.2节),这被称为自校准(Faugeras、Luong和Maybank 1992;Pollefeys、Koch和Van Gool 1999;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。然而,这种方法需要大量的图像才能准确。

图11.2校准图案:(a)三维目标(Quan和Lan1999)©1999 IEEE;(b)二维目标(Zhang2000)©2000 IEEE。注意,需要从这些图像中去除径向畸变,才能使用特征点进行校准。
平面校准图案
当使用有限的工作空间且具备精确的加工和运动控制平台时,一种良好的校准方法是将平面校准目标移动到工作空间内,并利用已知的三维点位置进行校准。这种方法有时被称为N-平面校准法(Gremban、Thorpe和Kanade 1988;Champleboux、Lavall e等1992b;Grossberg和Nayar 2001),其优点在于每个相机像素都可以映射到空间中的一个独特的三维点,这不仅考虑
了由校准矩阵K建模的线性效应,还考虑了非线性效应,如径向畸变(第11.1.4节)。
通过在相机前挥动平面校准图案(图11.2b),可以获得一个较为简便但精度较低的校准。在这种情况下,需要结合内参恢复图案的姿态。在~此技术中,每张输入图像用于计算一个单独的单应性(8.19–8.23)H,将平面校准点(Xi,Yi,1)映射到图像坐标(xi,yi),
(11.1)
其中,ri是R的前两列,~表示至多按比例相等。从这些数据中,张(2000)展示了如何对B = K-TK-1矩阵中的九个条目形成线性约束,从而可以使用矩阵恢复校准矩阵K。

图11.3从消失点进行校准:(a)任意一对有限消失点
(i,j)可用于估计焦距;(b)消失点的正交中心
三角形给出了图像c的图像中心。
平方根和逆运算。矩阵B在射影几何中被称为绝对圆锥(IAC)的像,常用于相机校准(Hartley和Zisserman 2004,第8.5节)。如果只需要恢复焦距,则可以采用下面描述的更简单的使用消失点的方法。
在实际应用中,校准的一个常见情况是相机拍摄到具有长条形图案的制造或建筑场景,如盒子或建筑物墙壁。在这种情况下,我们可以将对应于三维平行线的二维线相交,以计算它们的消失点,具体方法见第7.4.3节,并利用这些消失点来确定内参和外参(Caprile和Torre 1990;Becker和Bove 1995;Liebowitz和Zisserman 1998;Cipolla、Drummond和Robertson 1999;Antone和Teller 2002;Criminisi、Reid和Zisserman 2000;Hartley和Zisserman 2004;Pflugfelder 2008)。
假设我们检测到了两个或更多的正交消失点,且这些消失点都是有限的,即它们不是由图像平面上看似平行的线获得的(图11.3a)。我们还假设校准矩阵K的形式简化,其中只有焦距未知(2.59)。通常,在进行粗略的3D建模时,可以假设光学中心位于图像中心,长宽比为1,并且没有倾斜。在这种情况下,消失点的投影方程可以表示为
= ri , (11.2)
其中,pi对应于一个基本方向(1,0,0)、(0,1,0)或(0,0,1),ri

图11.4单视图测量(Criminisi、Reid和Zisserman 2000)©2000斯普林格:(a)输入图像显示了从两个水平消失点计算出的三个坐标轴(这些消失点可以从棚屋的侧边确定);(b)三维重建的新视图。
是旋转矩阵R的第i列。
从旋转矩阵的列之间的正交性,我们有
ri·rj ~(xi - cx)(xj - cx)+(yi - cy)(yj - cy)+ f2 = 0,i j
(11.3)
从中我们可以得到f2的估计值。请注意,随着消失点逐渐靠近图像中心,该估计值的准确性会提高。换句话说,最好将校准图案在45°轴附近倾斜一定角度,如图11.3a所示。一旦确定了焦距f,就可以通过归一化(11.2)的左侧并取叉积来估计R的各个列。或者,也可以使用正交普罗克鲁斯特算法(8.32)。
如果三个消失点在同一图像中均可见且有限,则可以将图像中心估计为由这三个消失点形成的三角形的垂心(Caprile和Torre 1990;Hartley和Zisserman 2004,第8.6节)(图11.3b)。然而,在实际操作中,使用非线性最小二乘法重新估计任何未知的内部校准参数更为准确(11.14)。
一个有趣的视点估计和相机校准应用是Criminisi、Reid和Zisserman(2000)开发的单视图测量系统。该系统允许人们交互式地测量高度和其他尺寸,以及构建分段平面3D模型,如图11.4所示。
系统的第一步是在地面平面上识别两个正交的消失点以及垂直方向上的消失点,这可以通过在图像中绘制一些平行线来完成。或者,可以使用第7.4.3节讨论的自动化技术或Schaffalitzky和Zisserman(2000)的方法。然后,用户可以在图像中标记几个尺寸,例如参考物体的高度,系统可以自动计算另一个物体的高度。墙壁和其他平面假象(几何形状)也可以勾画并重建。
在克里米尼西、里德和齐瑟曼(2000)最初开发的公式中,系统生成一个仿射重建,即仅已知每个轴上的独立缩放因子。通过假设相机校准到未知焦距,可以构建一个更有用的系统,这可以从正交(有限)消失方向恢复,正如我们在第11.1.1节中所描述的那样。一旦完成这一过程,用户可以在地面上指定一个原点,并指出另一个已知距离外的点。由此,地面上的点可以直接投影到三维空间中,而地面上方的点与它们的地平面投影配对后也可以被恢复。这样,场景的完全度量重建就成为可能。
练习11.4要求你实现这样一个系统,并用它来建模一些简单的3D场景。第13.6.1describes节介绍了其他可能的多视角建筑重建方法,包括一个使用消失点建立三维线方向和平面法向量的交互式分段平面建模系统(Sinha,Steedly等,2008)。
11.1.3旋转运动
当没有校准目标或已知结构,但可以围绕相机的前节点旋转(或者,等效地,在一个所有物体都远离的大型开放环境中工作)时,可以通过假设从一组重叠图像中对相机进行校准
如图11.5所示,它正在进行纯旋转运动(Stein1995;Hartley
1997b;Hartley、Hayman等人2000;de Agapito、Hayman和Reid 2001;Kang和Weiss 1999;Shum和Szeliski 2000;Frahm和Koch 2003)。当使用完整的360°运动进行校准时,可以获得非常精确的焦距f估计值,因为这种估计的准确性与最终圆柱全景图中的总像素数成正比(第8.2.6节)(Stein 1995;Shum和Szeliski 2000)。
要使用这项技术,我们首先计算所有重叠图像对之间的单应性矩阵ij,如公式(8.19–8.23)所示。然后,利用观察到的现象,首次在公式(2.72)中提出并在公式(8.38)中详细探讨,即每个单应性矩阵都通过(未知的)校准矩阵Ki与相机间旋转Rij相关。

图11.5使用手持摄像机拍摄的四幅图像,使用三维旋转运动模型进行配准,可用于估计摄像机的焦距(Szeliski和Shum1997)©2000 ACM。
Hij = KiRi Rj-1Kj-1 = KiRijKj-1。 (11.4)
获取校准的最简单方法是使用校准矩阵(2.59)的简化形式,假设像素为正方形且图像中心位于二维像素阵列的几何中心,即Kk =对角线(fk,fk,1)。我们从原始像素坐标中减去一半的宽度和高度,使得像素(x,y)=(0,0)位于图像中心。然后我们可以将公式(11.4)重写为
其中hij是H10的元素。
利用旋转矩阵R10的正交性质和(11.5)的右侧仅已知到一个比例因子这一事实,我们得到
h0 + h1 + f0-2h2 = h + h + f0-2h (11.6)
和
h00 h10 + h01 h11 + f0-2h02 h12 = 0. (11.7)
或
如果h00
h10 -h01
h11。 (11.9)
如果这两个条件都不满足,我们也可以计算第一(或第二)行~与第三行的点积。通过分析H10的列,同样可以得到f1的结果。如果两幅图像的焦距相同,我们可以取f0和f1的几何平均值作为估计的焦距f=√f1 f0。当有多组f的估计值时,例如来自不同的单应性变换,可以使用中位数作为最终估计值。对于固定参数相机Ki = K的情况,可以使用Hartley(1997b)的技术获得更一般的(上三角)K的估计值。Hartley、Hayman等人(2000)和de Agapito、Hayman和Reid(2001)讨论了时间变化校准参数和非静态相机情况下的扩展。
通过构建完整的360°全景图,可以显著提高相机参数的质量。因为如果焦距估计错误,当序列中的第一张图像与自身拼接时(图8.6),会导致间隙(或过度重叠)。由此产生的错位可用于改进焦距估计,并重新调整旋转估计,如第8.2.4节所述。围绕光轴旋转相机90°并重新拍摄全景图是检查纵横比和像素偏斜问题的好方法,当有足够的纹理时,生成完整的半球全景图也是不错的选择。
然而,最终,如第11.2.2节所述,可以使用固有参数和外在参数(旋转)的完整同时非线性最小化来获得校准参数(包括径向畸变)的最准确估计值。
当使用广角镜头拍摄图像时,通常需要建模镜头畸变,如径向畸变。正如第2.1.5节所述,径向畸变模型指出,观测图像中的坐标会根据其径向距离成比例地向中心偏移(桶形畸变)或远离中心(枕形畸变)(图2.13a–b)。最简单的径向畸变模型使用低阶多项式(参见公式(2.78)),
= x(1 + h1 r2 + h2 r4 ) = y(1 + h1 r2 + h2 r4 ),
其中(x,y) = (0,0)在径向畸变中心(2.77),r2 = x2 + y2,h1和h2称为径向畸变参数(Brown1971;Slama1980)。1
有时,x和之间的关系用相反的方式表示,即在右侧使用带撇号(最终)的坐标,x =(1 + 12 + 24)。如果我们将图像像素映射到(扭曲的)
可以使用多种技术来估计给定镜头的径向畸变参数,前提是数码相机在其捕捉软件中尚未完成此操作。最简单且最有用的方法之一是拍摄一个包含大量直线的场景图像,特别是那些与图像边缘对齐或靠近边缘的直线。然后调整径向畸变参数,直到图像中的所有直线都变得笔直,这通常被称为铅垂线法(Brown 1971;Kang 2001;El-Melegy和Farag 2003)。练习11.5给出了如何实现这种技术的一些更多细节。
另一种方法是使用多个重叠的图像,并将径向畸变参数的估计与图像对齐过程相结合,即扩展第8.3.1节中用于拼接的流程。Sawhney和Kumar(1999)采用了一种从粗到精的策略,结合了运动模型(平移、仿射、投影)层次结构和二次径向畸变校正项。他们使用直接(基于强度的)最小化方法来计算对齐。Stein(1997)则采用基于特征的方法,结合通用的3D运动模型(以及二次径向畸变),这需要比无视差旋转全景图更多的匹配点,但可能更为通用。更近期的方法有时同时计算未知的内部参数和径向畸变系数,这些系数可能包括高阶项或更复杂的有理或非参数形式(Claus和Fitzgibbon 2005;Sturm 2005;Thirthala和Pollefeys 2005;Barreto和Daniilidis 2005;Hartley和Kang 2005;Steele和Jaynes 2006;Tardif、Sturm等2009)。
当使用已知的校准目标时(图11.2),径向畸变估计可以融入其他内参和外参的估计中(张2000;哈特利和康2007;塔迪夫、斯特姆等人2009)。这可以视为在图11.7所示的一般非线性最小化流程中,在内参乘法框fC和透视分割框fP之间增加了一个阶段。(有关平面校准目标情况的更多细节,请参见练习11.6。)
当然,如第2.1.5节所述,有时可能需要更通用的镜头畸变模型,例如鱼眼和非中心投影。虽然这类镜头的参数化可能更为复杂(第2.1.5节),但通常可以采用使用已知三维位置的校准装置或通过场景的多个重叠图像进行自校准的方法(Hartley和Kang 2007;Tardif、Sturm和Roy 2007)。用于校正径向畸变的技术同样也可以用来减少色差,通过分别校准每个颜色通道来实现。
然后扭曲光线以获得空间中的三维光线,即,如果我们使用逆变形。
基于特征的对齐的一个常见实例是从一组二维点投影中估计物体的三维姿态。这种姿态估计问题也被称为外参校准,与我们将在第11.1节讨论的内部相机参数如焦距的内参校准相对。从三个对应点恢复姿态的问题,即所需最少信息量的问题,被称为透视三点问题(P3P),并扩展到更多点的问题,统称为PnP(Haralick,Lee等1994;Quan和Lan1999;Gao,Hou等2003;Moreno-Noguer,Lepetit和Fua2007;Persson和Nordberg2018)。
在本节中,我们将研究一些为解决此类问题而开发的技术,首先从直接线性变换(DLT)开始,它恢复了3×4相机矩阵,然后是其他“线性”算法,最后是统计最优迭代算法。
恢复相机姿态的最简单方法是形成一组类似于用于2D运动估计(8.19)的有理线性方程,从透视投影(2.55–2.56)的相机矩阵形式中得到,
(11.11)
(11.12)
其中(xi,yi)是测量的二维特征位置,(Xi,Yi,Zi)是已知的三维特征位置(图11.6)。与公式(8.21)类似,这个方程组可以通过在线性方式求解相机矩阵P中的未知数,方法是将方程两边的分母相乘。由于P在比例上是未知的,我们可以固定其中一个元素,例如p23 = 1,或者找到一组线性方程组的最小奇异向量。由此产生的算法称为直接线性变换(DLT),通常归功于Sutherland(1974年)。(关于更深入的讨论,请参见Hartley和Zisserman(2004年)。)为了计算P中的12个(或11个)未知数,至少需要知道3D和2D位置之间的六个对应关系。
与估计同态(8.21–8.23)的情况一样,通过直接最小化方程组(11.11–11.12),可以获得P中条目的更准确的结果
2“三点”算法实际上需要第四个点来解决四重模糊性。

图11.6通过直接线性变换和测量点对之间的视觉角度和距离进行姿态估计。
用少量迭代进行非线性最小二乘法。注意,与(11.11–11.12)中取X/Z和Y/Z值的比值不同,也可以取交叉
将3维向量(xi,yi,1)的图像测量值与三维射线(X,Y,Z)相乘,并将该交叉乘积的三个元素设为0。当将所得的三个方程解释为一组最小二乘约束时,实际上计算了两条射线之间角度的正弦平方。
一旦恢复了P中的条目,就可以通过观察方程(2.56)恢复内在校准矩阵K和刚性变换(R,t),
P = K[Rjt]. (11.13)
由于K是上三角矩阵(参见第2.1.4节中的讨论),因此可以使用RQ分解法从P的前3×3子矩阵中获得K和R(Golub和Van Loan,1996)。3
然而,在大多数应用中,我们对固有的校准矩阵K有一些先验知识,例如像素是方形的,偏斜非常小,图像中心接近图像的几何中心(2.57–2.59)。这些约束可以被纳入到K和(R,t)参数的非线性最小化过程中,如Section11.2.2所述。 在相机已经校准的情况下,即矩阵K已知(第11.1节),我们可以使用最少三个点进行姿态估计(Fischler和Bolles 1981;Haralick、Lee等人1994;Quan和Lan 1999)。这些线性PnP(透视n点)算法的基本观察是,任意一对二维点i和j之间的视角度必须与它们对应的三维点pi和之间的角度相同。
本书第一版(Szeliski 2010,第6.2.1节)以及(Quan和Lan 1999)中详细推导了这种方法。这些文献中,作者提供了该方法及其他技术的精度结果,后者虽然使用较少的点数,但需要更复杂的代数运算。Moreno-Noguer、Lepetit和Fua(2007)的文章回顾了其他替代方案,并提出了一种复杂度更低且通常产生更准确结果的算法。Terzakis和Lourakis(2020)则在一篇更为近期的论文中综述了过去十年发表的相关研究。
不幸的是,由于最小化PnP解决方案可能非常敏感于噪声,并且还存在浮雕模糊问题(例如深度反转)(第11.4.5节),因此明智的做法是使用第11.2.2节中描述的迭代技术来优化PnP的初始估计。另一种姿态估计算法是从一个缩放后的正射投影模型开始,然后使用更精确的透视投影模型逐步改进这一初始估计(DeMenthon和Davis1995)。正如论文标题所述,该模型的魅力在于它可以“用25行[Mathematica]代码”实现。
基于CNN的姿态估计
与其他计算机视觉领域一样,深度神经网络也被应用于姿态估计。一些具有代表性的论文包括Xiang、Schmidt等人(2018年)、Oberweger、Rad和Lepetit(2018年)、Hu、Hugonot等人(2019年)、Peng、Liu等人(2019年)以及(Hu、Fua等人2020年)关于物体姿态估计的研究,还有Kendall和Cipolla(2017年)及Kim、Dunn和Frahm(2017年)在第11.2.3节中讨论的位置识别研究。此外,围绕从RGB-D图像中估计姿态的社区也非常活跃,最近的论文(Hagelskjær和Buch2020;Labb、Carpentier等人2020)在该领域进行了评估。
BOP(6DOF物体姿态基准)(Hoda,Michel等人,2018)。4
估计姿态最准确且灵活的方法是直接最小化二维点的平方(或鲁棒)重投影误差,作为未知姿态参数(R;t)的函数,并可选地使用非线性最小二乘法(Tsai1987;Bogart1991;Gleicher和Witkin1992)来最小化K。我们可以将投影方程表示为
xi = f(pi;R
;t;K) (11.14)
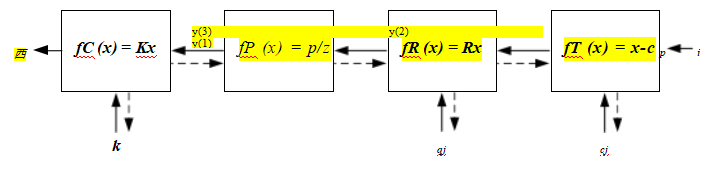
图11.7通过一系列变换f(k)将三维点pi投影到二维测量值xi,每项变换都由其自身的参数集控制。虚线表示在反向传播过程中计算偏导数时的信息流。
ENLP =
(11.15)
其中,ri = i -
i是当前残差向量(预测位置的二维误差)和
偏导数是关于未知姿态参数(旋转、平移,以及可选的校准)的。我们首次在第4.1.3节的(4.15)中介绍的鲁棒损失函数P,用于减少异常对应的影响。请注意,如果2D特征位置有完整的2D协方差估计,则上述平方范数可以由逆点协方差矩阵加权,如公式(8.11)所示。
一个更容易理解(和实现)的上述非线性回归问题可以通过将投影方程重写为一系列更简单的步骤来构建,每个步骤都通过简单的变换如平移、旋转或透视除法来转换一个四维齐次坐标pi(图11.7)。由此产生的投影方程可以表示为
y (1) = fT (pi ; cj) = pi - cj , (11.16)
y (2) = fR (y (1) ; qj) = R (qj) y (1) , (11.17)
xi = fC(y(3);k)= K(k) y(3)。 (11.19)
请注意,在这些方程中,我们用索引j对相机中心cj和相机旋转四元数qj进行了索引,以防使用校准对象的多个姿态(参见第11.4.2节)。我们还使用相机中心cj而不是世界平移tj,因为这是一个更自然的参数来估计。
这一组变换的链式结构的优点在于,每个变换都对其参数和输入具有简单的偏导数。因此,一旦预测值
参数(cj;qj;k),我们可以使用链式法则得到所有需要的偏导数
(11.20)
其中p(k)表示正在优化的参数向量之一。(同样的“技巧”在神经网络中作为反向传播的一部分使用,我们在Figure5.31中介绍过。)
在这个公式中,可以显著简化的一个特殊情况是旋转更新的计算。不必直接计算3×3旋转矩阵R(q)关于单位四元数元素的导数,而是可以在当前旋转矩阵前加上方程(2.35)给出的增量旋转矩阵△R(!),然后计算变换对这些参数的偏导数,这会导致一个简单的逆向链偏导数与输出的三维向量的叉积,如方程(2.36)所解释的那样。
姿态估计的一个广泛应用是增强现实,其中虚拟的3D图像或注释被叠加到实时视频流上,无论是通过透明眼镜(前置显示)还是普通计算机或移动设备屏幕(Azuma,Baillot等2001;Haller,Billinghurst和Thomas 2007;Billinghurst,Clark和Lee 2015)。在某些应用中,卡片或书籍上的特殊图案会被跟踪以实现增强效果(Kato,Billinghurst等2000;Billinghurst,Kato和Poupyrev 2001)。对于桌面应用程序,嵌入增强鼠标中的摄像头可以跟踪打印在鼠标垫上的点阵,使用户能够控制其在三维空间中的六个自由度的位置和方向(Hinckley,Sinclair等1999)。如今,追踪已知目标如电影海报的功能被用于一些基于手机的增强现实系统,例如Facebook的Spark AR。
有时,场景本身提供了一个方便的追踪对象,例如用于镜头后方摄像机控制的矩形桌面(Gleicher和Witkin 1992)。在户外地点,如电影拍摄现场,通常会在场景中放置特殊标记,比如鲜艳的彩色球体,以便更容易找到和追踪它们(Bogart 1991)。在较旧的应用中,使用了测量技术来确定这些球体的位置。
在拍摄前,现在更常见的是将结构从运动直接应用到影片本身(第11.5.2节)。
练习8.4要求你为增强现实应用程序实现一个跟踪和姿态估计系统。
姿态估计最令人兴奋的应用之一是在位置识别领域,这既可用于桌面应用程序(“我拍的这张度假照片是在哪里拍的?”),也可用于移动智能手机应用程序。后者不仅包括根据手机图像确定当前位置,还提供导航方向或在图像中标注有用信息,如建筑物名称和餐厅评论(即便携式增强现实)。这个问题也常被称为视觉(或基于图像)定位(Se,Lowe,和Little 2002;Zhang和Kosecka 2006;Janai,
G ney等人,2020年,第13.3节)或视觉位置识别(Lowry,S.nderhauf等人,2015)。
一些定位识别方法假设照片包含建筑场景,可以使用消失方向预先校正图像以方便匹配(Robertson和Cipolla 2004)。其他方法则利用一般的仿射协变兴趣点进行宽基线匹配(Schaffalitzky和Zisserman 2002),在2005年国际计算机视觉竞赛中获胜的参赛作品(Szeliski 2005)采用了这种方法(Zhang和Kosecka 2006)。Snavely、Seitz和Szeliski(2006)提出的“照片旅游”系统(第14.1.2节)首次将这些理念应用于大规模图像匹配和(隐式)从互联网照片集合中进行位置识别,这些照片是在各种观看条件下拍摄的。
位置识别的主要难点在于处理像Flickr (Philbin,Chum等2007;Chum,Philbin等2007;Philbin,Chum等2008;Irschara,Zach等2009;Turcot和Lowe 2009;Sattler,Leibe和Kobbelt 2011,2017)或商业捕获数据库(Schindler,Brown和Szeliski 2007;Klingner,Martin和Roseborough 2013;Tori,Arandjelovi等2018)中极其庞大的社区(用户生成)照片集合。常见元素如树叶、标志和普通建筑元素的普遍出现进一步增加了任务的复杂性(Schindler,Brown
,和Szeliski 2007;Jegou,Douze,和Schmid 2009;Chum和Matas 2010b;Knopp,Sivic和Pajdla 2010;Tori,Sivic等2013;Sattler,Havlena等2016)。图7.26展示了一些来自社区照片集合的位置识别结果,而图11.8则展示了更密集的商业捕获数据集的样本结果。在后一种情况下,相邻数据库图像之间的重叠可以用来验证和剔除潜在匹配项,即要求查询图像与附近的重叠部分相匹配——

图11.8基于特征的位置识别(Schindler、Brown和Szeliski2007)©
2007 IEEE:(a)三组重叠的街道照片;(b)手持相机拍摄的照片和(c)相应的数据库照片。
在匹配之前先比对数据库图像。类似的想法已被用于改进全景视频序列中的位置识别(Levin和Szeliski 2004;Samano、Zhou和Calway 2020),以及将图像序列中的局部SLAM重建与预计算地图进行匹配以提高可靠性(Stenborg、Sattler和Hammarstrand 2020)。在建筑物和购物中心内识别室内位置也面临一系列挑战,包括无纹理区域和重复元素(Levin和Szeliski 2004;Wang、Fidler和Urtasun 2015;Sun、Xie等2017;Taira、Okutomi等2018;Taira、Rocco等2019;Lee、Ryu等2021)。地面图像与航拍图像的匹配研究也已开展(Kaminsky、Snavely等2009;Shan、Wu等2014)。
一些早期关于位置识别的研究围绕牛津5公里和巴黎6公里数据集(Philbin,Chum等,2007,2008;Radenovi,Iscen等,2018)以及维也纳(Irschara,Zach等,2009
)和照片旅游(Li,Snavely,和Huttenlocher,2010)数据集展开,后来又围绕7个室内RGB-D场景数据集(Shotton,Glocker等,2013)和剑桥地标(Kendall,Grimes,和Cipolla,2015)进行。NetVLAD论文(Arandjelovic,Gronat等,2016)在谷歌街景时间机器数据上进行了测试。目前,最广泛使用的视觉定位数据集是在长期视觉定位基准6收集的,包括如亚琛日夜间(Sattler,Maddern等,2018)和InLoc (Taira,Okutomi等,2018)。虽然大多数定位系统基于地面图像集合工作,但也可以根据纹理数字高程(地形)模型重新定位,用于户外(非城市)应用(Baatz,Saurer等。
Al.2012;Brejcha,Luk et al
.2020)。
最近的一些定位方法使用深度网络生成特征描述符(Arandjelovic,Gronat等2016;Kim,Dunn和Frahm 2017;Torii,Arandjelovi等2018;Radenovi,Tolias和Chum
2019;Yang,Kien Nguyen等2019
;Sarlin,Unagar等2021),进行大规模实例检索(Radenovi,Tolias和Chum 2019;Cao,Araujo和Sim 2020;Ng
,Balntas等2020;Tolias,Jenicek和Chum 2020;Pion,Humenberger等2020和第6.2.3节),将图像映射到3D场景坐标(Brachmann和Rother 2018),或执行端到端场景坐标回归(Shotton,Glocker等2013),绝对姿态回归(APR)(Kendall,Grimes和Cipolla 2015;Kendall和Cipolla 2017),或相对姿态回归(RPR)(Melekhov,Ylioinas等2017;Balntas,Li和Prisacariu 2018)。这些技术的最新评估表明,基于特征匹配随后进行几何姿态优化的经典方法通常在准确性和泛化能力方面优于姿态回归方法(Sattler,Zhou等2019;Zhou,Sattler等2019;Ding,Wang等2019;Lee,Ryu等2021;Sarlin,Unagar等2021)。
长期视觉定位基准有一个排行榜,列出了表现最好的定位系统。在CVPR 2020研讨会和挑战中,一些获胜的en-
尝试基于最近的检测器、描述符和匹配器,如SuperGlue (Sarlin,DeTone等2020)、ASLFeat (Luo,Zhou等2020)和R2D2 (Revaud,Weinzaepfel等2019)。其他表现良好的系统包括HF-Net (Sarlin,Cadena等2019)、ONavi (Fan,Zhou等2020)和D2-Net (Dusmanu,Rocco等2019)。更近的趋势是使用深度神经网络或变压器来建立密集的粗到精匹配(Jiang,Trulls等2021;Sun,Shen等2021)。
位置识别的另一种变体是地标自动发现,即经常拍摄的对象和地点。Simon、Snavely和Seitz(2007)展示了如何通过分析照片旅游中三维建模过程中构建的匹配图来发现这些对象。最近的研究扩展了这种方法,使用高效的聚类技术处理更大的数据集(Philbin和Zisserman 2008;Li、Wu等2008;Chum、Philbin和Zisserman 2008;Chum和Matas 2010a;Aranđelovi和Zisserman 2012),结合GPS和文本标签等元数据与视觉搜索(Quack、Leibe和Van Gool 2008;Crandall、Backstrom
等2009;Li、Snavely等2012),并利用多个描述符在微型空中车辆导航中实现实时性能(Lim、Sinha等2012)。现在甚至可以基于多个松散标记图像中的共现情况自动关联对象标签(Simon和Seitz 2008;Gammeter、Bossard等2009)。
按地点组织世界照片收藏的概念甚至已经被重新定义

图11.9使用天体测量法定位星场,https://astrometry.net。(a)输入星场和一些选定的星四边形。(b)星体C和D的二维坐标相对于由A和B定义的单位正方形进行编码。
最近扩展到将宇宙中(天文学)的所有照片组织在一个名为天体测量的应用程序中。7用于匹配任意两个星场的技术是取附近恒星的四重组合(一对恒星和另一对位于它们直径内的恒星),通过使用内切正方形作为参考框架来编码第二对点的相对位置,形成一个30位的几何哈希值,如图11.9所示。然后使用传统信息检索技术(为天空图集的不同部分构建的k-d树)来查找匹配的四重组合作为潜在的星场位置假设,这些假设可以通过相似性变换进行验证。
从一组对应的图像位置和已知的相机位置确定一个点的三维位置的问题被称为三角测量。这个问题与我们在第11.2节中研究的姿态估计问题相反。
解决这个问题最简单的方法之一是找到与相机{Pj = Kj [Rj jtj ]}观察到的二维匹配特征位置{xj }对应的全部三维射线最近的三维点p,其中tj =—Rj cj,cj为第j个相机中心(2.55–2.56)。
如图Figure11.10所示,这些射线从cj出发,方向为j = N(Rj-1Kj-1xj),
其中N(v)将向量v归一化为单位长度。这条射线上与p最近的点,即
我们用qj = cj + dj j来表示,以使距离最小
Ⅱqj — pⅡ2 = Ⅱcj + dj j — pⅡ2 ; (11.21)
在dj = j·(p—cj)处取最小值。因此,
qj = cj + (j )(p — cj) = cj + (p — cj) Ⅱ ; (11.22)

图11.10通过查找最接近所有光学光线cj + dj j的点p来实现三维点三角化。
在公式(2.29)的符号中,p和qj之间的平方距离为
r = Ⅱ(I - j )(p - cj )Ⅱ2 = Ⅱ(p - cj )丄 Ⅱ2 . (11.23)
p的最优值,即最接近所有光线的值,可以作为一个规则计算。
最小二乘问题,通过求和所有r并找到p的最优值,
(11.24)
另一种替代公式,更具有统计学上的最佳性,如果某些摄像机比其他摄像机更接近于三维点,则可以产生显著更好的估计值,即最小化测量方程中的残差
其中(xj,yj)是测量的二维特征位置,{p0()... p2()}是相机矩阵Pj中的已知条目(Sutherland1974)。
与方程(8.21、11.11和11.12)一样,这组非线性方程可以通过乘以分母的两边转换为一个线性最小二乘问题,再次得到直接的线性变换(DLT)形式。请注意,如果我们使用齐次坐标p =(X,Y,Z,W),则所得方程组是齐次的。
最佳解决方法是奇异值分解(SVD)或特征值问题(寻找最小的奇异向量或特征向量)。如果我们设W = 1,可以使用常规线性最小二乘法,但所得系统可能奇异或条件不良,即当所有视射线平行时,这种情况发生在远离相机的点上。
因此,通常最好使用齐次坐标来参数化三维点,特别是当我们知道相机与这些点之间的距离可能相差很大时。当然,无论选择何种表示方法,使用非线性最小二乘法(如公式8.14和8.23所述)来最小化观测集(11.25–11.26),都优于使用线性最小二乘法。
对于两个观测点的情况,事实证明,能够精确最小化真实重投影误差(11.25–11.26)的点p的位置可以通过六次多项式方程的解来计算(Hartley和Sturm 1997)。三角测量中需要注意的另一个问题是手性问题,即确保重建的点位于所有相机前方(Hartley 1998)。虽然这并不总是可以保证的,但一个有用的启发式方法是取那些位于相机后方的点,因为它们的光线是发散的(想象图11.10中的光线彼此远离),并将这些点设置在无穷远平面上,通过将它们的W值设为0。
到目前为止,在我们对三维重建的研究中,一直假设要么已知三维点的位置,要么已知三维相机的姿态。在本节中,我们将首次探讨运动从结构法,即从图像对应关系同时恢复三维结构和姿态。特别是,我们研究仅基于两帧点对应的技术。我们将这一部分分为经典“n点”算法的研究、特殊情况(退化情况)、投影(未校准)重建以及未知内参的相机自校准。
考虑图11.11,该图展示了从两个相机视角观察到的三维点p,这两个相机的相对位置可以通过旋转R和平移t来编码。由于我们对相机的位置一无所知,不失一般性,可以将第一个相机设置在原点c0 = 0,并处于标准方向R0 = I。
在第一个图像中,在位置0和z距离处观察到的3D点p0 = d00

图11.11极线几何:向量st=c1-c0、p-c0和p-c1共面,并定义了以像素测量值x0和x1表示的基本极线约束。
d0通过变换映射到第二个图像中
d11 = p1 = Rp0 + t = R (d00) + t; (11.27)
其中j = Kj-1xj是(局部)射线方向向量。取两边的叉积(交换顺序),以消除右边的t,得到8
d1 [t]×1 = d0 [t]× R0 . (11.28)
两边与1取点积,得到
d0 ([t]× R)0 = d1 [t]×1 = 0; (11.29)
因为右边是一个具有两个相同元素的三重乘积。(另一种说法是,交叉乘积矩阵[t]×是斜对称的,并且当用同一个向量进行前乘和后乘时返回0。)
E 0 = 0; (11.30)
在哪里
E = [t]× R (11.31)
8交叉乘积算子[]×在(2.32)中被引入。
使光线0和1在三维空间中相交于点p,连接这两点的向量
相机中心c1−c0 =−R1t和对应于像素x0和x1的光线,即
(0 , R-11, −R-1t) = (R0 , 1, −t) = 1 · (t × R0 ) = ([t]× R)0 = 0. (11.32)
请注意,本质矩阵E将图像0中的点0映射到图像1中的直线l1=E0=[t]×R0,因为l1=0(图11.11)。所有这样的直线都必须穿过第二个极线e1,因此定义为E的左奇异向量,具有0的奇异值,或者等价地,向量t在图像1中的投影。这些关系的对偶(转置)给出了第一个图像中的极线l0 = ET 1和e0作为E的零值右奇异向量。
八点算法。鉴于这一基本关系(11.30),我们如何利用它来恢复编码在本质矩阵E中的相机运动?如果我们有N个对应的测量值{(xi0,xi1)},我们可以形成N个关于E的九个元素= {e00... e22 }的齐次方程,
| +xi1e02 | + | ||
| xi0yi1e00 +yi0yi1e11 xi0e20 +yi0e21 | +yi1e12 +e22 | + = 0 | (11.33) |
[xi1 x]⊗E = Zi⊗E = Zi·f = 0, (11.34)
其中⊗表示矩阵元素的逐元素乘法和求和,zi
f是Zi = i1和E矩阵的向量化形式。9给定N≥8如下
通过方程,我们可以使用SVD计算E中元素的估计值(在比例上)。
在存在噪声测量的情况下,这个估计值与统计最优有多接近?如果你查看(11.33)中的条目,可以看到有些条目是像xi0yi1这样的图像测量的乘积,而其他则是直接的图像测量(甚至是对角线)。如果测量的噪声相当,那么这些测量乘积项的噪声会被乘积中的另一个元素放大,这可能导致非常糟糕的缩放效果,例如,坐标较大的点(远离图像中心)的影响异常大。
9我们用f代替e来表示E的向量化形式,以避免与极点ej混淆。
为了抵消这一趋势,Hartley(1997a)建议将点坐标进行转换和缩放,使其质心位于原点,且其方差为1,即:
= s(xi—μx) (11.35)
i
=s(yi-μy) (11.36)
使得εi i = εi i=0~和ε
i +εi
= 2n,其中n是点数。10
一旦从变换坐标中计算出基本矩阵E
在(11.35–11.36)中进行尺度操作后,原始本质矩阵E可以恢复为
E = TT0 . (11.37)
在他的论文中,哈特利(1997a)将他提出的重新归一化策略与张(1998a,b)等人提出的其他距离度量方法的改进进行了比较,并得出结论,在大多数情况下,他的简单重新归一化方法与(或优于)替代技术一样有效。托尔和菲茨吉本(2004)推荐了该算法的一个变体,即E的上2×2子矩阵的范数设为1,并证明它在面对2D坐标变换时具有更好的稳定性。
7点算法。由于E是秩亏的,实际上我们只需要七个形式如公式(11.34)的对应关系来估计这个矩阵(Hartley1994a;Torr和Murray1997;Hartley和Zisserman2004)。在RANSAC稳健拟合阶段使用较少的对应关系的优势在于需要生成更少的随机样本。从这七个齐次方程组(我们可以将其堆叠成一个7×9矩阵用于SVD分析)中,可以找到两个独立向量,记为f0和f1,使得zi·fj = 0。这两个向量可以转换回3×3矩阵E0和E1,它们张成了解空间的基。
E = QE0 + (1 — Q)E1 . (11.38)
为了找到Q的正确值,我们观察到E的行列式为零,因为它秩不足,因此
j QE0 + (1 — Q)E1 j = 0. (11.39)
10更准确地说,Hartley(1997a)建议对点进行缩放,“使与原点的平均距离等于√2”,但单位方差的启发式方法计算速度更快(不需要对每个点进行平方根运算),并且应该产生可比的改进。
这给我们一个关于Q的三次方程,它有一个或三个解(根)。将这些值代入(11.38)以获得E,我们可以用这个基本矩阵与其他未使用的特征对应关系进行测试,以选择正确的那个。
归一化的“八点算法”(Hartley1997a)和上述描述的七点算法并不是估计相机运动的唯一方法。其他变体包括五点算法,该算法需要找到十阶多项式的根(Nist2004),以及处理特殊(受限)运动或场景结构的变体,这些将在本节后面讨论。由于这些算法使用较少的点来计算其估计值,因此在作为随机采样(RANSAC)策略的一部分时,对外部异常值的敏感度较低。11
恢复t和R。一旦获得了本质矩阵E的估计值,就可以估算出平移向量t的方向。请注意,无论使用多少相机或点,仅凭图像测量无法恢复两台相机之间的绝对距离。要确定最终的比例、位置和方向,总是需要关于相机和点的绝对位置或距离的知识,这在摄影测量中通常被称为地面控制点。
为了估计这个方向,观察到在理想的无噪声条件下,基本矩阵E是奇异的,即TE = 0。当对E进行SVD时,这种奇异性表现为一个0的奇异值,
× R =
UΣVT =
(11.40)
当从噪声测量中计算出E时,与最小奇异值相关的奇异向量给出了。(另外两个奇异值应该相似,但通常不等于1,因为E只是在未知尺度上计算的。)
一旦恢复了,我们如何估计相应的旋转矩阵R?回想一下,交叉乘积算子[]×(2.32)将一个向量投影到一组正交基向量上,包括,零出分量,并将另外两个向量旋转90°,
= s0×s1。根据公式(11.40和11.41),我们得到
E = [] × R = SZR90. STR = UΣVT ; (11.42)
由此我们可以得出结论,S = U。回想一下,对于一个无噪声的基本矩阵,(Σ = Z),因此
R90. UTR = VT (11.43)
R = UR. VT . (11.44)
不幸的是,我们只知道E和一个符号。此外,矩阵U和V
不能保证是旋转(你可以翻转它们的符号,仍然得到一个有效的SVD)。因此,我们必须生成所有四个可能的旋转矩阵
R = ±UR90. VT
(11.45)
并保留行列式jRj = 1的两个。为了区分剩余的一对潜在旋转,它们形成了一对扭曲的旋转(Hartley和Zisserman 2004,第259页),我们需要将它们与平移方向±的两种可能符号配对,并选择在两台相机前看到最多点数的组合。12
点必须位于相机前方,即沿从相机发出的视线方向处于正距离处,这一特性被称为手性(Hartley1998)。除了确定旋转和平移的符号外,如上所述,重建中点的手性(距离的符号)也可以用于RANSAC过程(连同重投影误差)来区分可能和不太可能的配置。13手性还可以用于将射影重建(第11.3.3节和第11.3.4节)转换为准仿射重建(Hartley1998)。
在某些情况下,专门设计的算法可以利用已知(或猜测)的摄像机布置或3D结构。
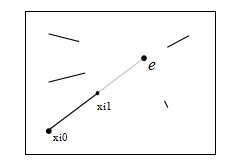
图11.12纯平移摄像机运动导致视觉运动,其中所有点都向(或远离)一个共同的扩展焦点(FOE)e移动。因此,它们满足三重乘积条件(x0,x1,e)= e·(x0×x1)= 0。
纯投影(已知旋转)。在已知旋转的情况下,我们可以预先旋转第二张图像中的点,以匹配第一张图像的观察方向。结果得到的三维点集都会朝向(或远离)扩展焦点(FOE),如图11.12.14所示。由此产生的本质矩阵E(在无噪声情况下)是对称的,因此可以通过设置eij =—eji和eii = 0来更直接地估计(11.33)。现在,两个具有非零视差的点就足以估计FOE。
通过最小化三重乘积,可以得到FOE估计值的更直接推导
(11.46)
(yi0 — yi1)e0 + (xi1 — xi0)e1 + (xi0yi1 — yi0xi1)e2 = 0. (11.47)
请注意,与八点算法一样,在计算该估计值之前,建议将二维点标准化为具有单位方差。
在有大量无穷远点可用的情况下,例如拍摄户外场景或相机运动相对于远处物体较小时,这提示了一种估计相机运动的替代RANSAC策略。首先,选择一对点来估计旋转,希望这两点都位于无穷远(非常远离相机)。然后,计算FOE并检查残差误差是否小(表明与该旋转假设一致),以及向或远离极点(FOE)的运动是否都在同一方向(忽略可能受噪声污染的微小运动)。
《星际迷航》和《星球大战》的粉丝们会认出这是“跃迁到超空间”的视觉效果。
纯旋转。纯旋转的情况会导致对本质的估计退化
矩阵E和变换方向。首先考虑旋转矩阵的情况
众所周知,FOE的估计值是退化的,因为xi0≈xi1,因此(11.47)也是退化的。类似的论证表明,本质矩阵的方程(11.33)也是秩亏的。
这表明,在计算完整的本质矩阵之前,可以先使用(8.32)计算旋转估计R,可能只需要少量的点,然后在继续进行完整的E计算之前旋转点,再计算残差。
主导平面结构。当场景中存在主导平面时,退化算法可以用来更可靠地恢复基础矩阵,而退化算法测试的是是否太多对应点共面(Chum、Werner和Matas 2005)。
正如你从前面的特殊情况可以看出,存在许多不同的两帧运动结构的专门案例以及许多合适的替代技术。Kneip和Furgale(2014)开发的OpenGV库包含了这些算法的开源实现。15
在许多情况下,比如尝试从互联网或未知相机拍摄的旧照片中构建3D模型时,这些照片没有任何EXIF标签,我们无法提前知道输入图像的固有校准参数。在这种情况下,我们可以静态地估计两帧重建,尽管真实的度量结构可能不可用,例如,世界中的正交线或平面最终可能不会被重建为正交。
考虑我们用来估计基本矩阵E(11.30–11.32)的推导。在未校准的情况下,我们不知道校准矩阵Kj,因此我们不能使用正态-
射线方向为j = Kj-1xj。相反,我们只能访问图像坐标xj,
因此,基本矩阵方程(11.30)变为
E1 = xK TEK0-1x0 = xFx0 = 0; (11.48)
F = K TEK0-1
(11.49)
称为基本矩阵(Faugeras1992;Hartley、Gupta和Chang1992;Hartley和Zisserman2004)。
与基本矩阵一样,基本矩阵(原则上)是秩为2的,
(11.50)
其最小的左奇异向量表示图像1中的epipolee1,而其最小的右奇异向量是e0(图11.11)。基本矩阵可以分解为一个斜对称交叉乘积矩阵[e]×和一个单应H,
F = [e]× . (11.51)
从(11.49)式原则上讲,同态应等于
= K TRK0—1 ; (11.52)
不能从F中唯一恢复,因为任何形式为/ = + evT的同态结果
在同一个F矩阵中。(注意,[e]×会湮灭e的任何倍数。)
这些有效的单应性变换H中的任何一个都映射了场景中的一张图像到另一张图像中的某个平面。如果不选择四个或更多共面对应点来计算H(类似于猜测E的旋转方式),或者通过H映射一张图像中的所有点并查看哪些点与另一张图像中的相应位置对齐,就无法提前判断是哪一个。这种表示通常被称为平面加视差(Kumar、Anandan和Hanna 1994;Sawhney 1994),并在Section2.1.4中进行了更详细的描述。
~为了创建场景的投影重建,我们可以选择任何满足方程(11.49)的有效单应矩阵H。例如,采用类似于方程(11.40–11.44)的技术,我们得到
F = [e]× = SZR90. ST = UΣVT (11.53)
因此 ~
H = UR. VT ; (11.54)其中,最小值的奇异值矩阵被合理的替代值(比如中间值)所取代。16然后我们可以形成一对相机矩阵
16 Hartley和Zisserman(2004,第256页)建议使用=[e]×F(Luong和Vi ville1996
),该方法可将
飞机上的摄像头在无穷远处。
712 计算机视觉:算法和应用,第2版(最终稿,2021年9月)
由此可以使用三角测量法计算场景的投影重建(第11.2.4节)。
虽然投影重建本身可能没有用处,但通常可以升级为仿射或度量重建,如下所述。即使不进行这一步骤,基础矩阵F在寻找额外对应点时仍然非常有用,因为所有这些对应点都必须位于相应的极线上,即图像0中的任何特征x0都必须在其对应的图像1中的极线l1 = Fx0上,假设
11.3.4自校准
结构从运动计算的结果如果能获得度量重建会更有用,即平行线保持平行,正交墙面保持垂直,重建模型是现实的缩放版本。多年来,已经开发了大量自校准(或自动校准)技术,用于将投影重建转换为度量重建,这相当于恢复与每张图像相关的未知校准矩阵Kj(Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。
在已知场景附加信息的情况下,可以采用不同的方法。例如,如果场景中有平行线,可以利用三个或更多消失点来建立无穷远平面的单应性,从而恢复焦距和旋转。如果观察到了两个或多个有限正交消失点,则可以使用基于消失点的单图像校准方法(第11.1.1节)。
在缺乏此类外部信息的情况下,仅凭对应关系无法恢复每个图像的完全参数化的独立校准矩阵Kj。为了理解这一点,考虑所有相机矩阵Pj = Kj [Rj jtj ]将世界坐标pi =(Xi,Yi,Zi,Wi)投影到屏幕坐标xij ~ Pj pi的集合。现在再考虑通过任意4×4投影变换H~转换三维场景{pi },得到一个新的模型,其中点pi=Hpi。将每个Pj矩阵后乘以H-1仍然会产生相同的屏幕坐标,并且可以通过对新的相机矩阵Pj=Pj H-1应用RQ分解来计算新的校准矩阵集。
因此,所有自校准方法都假设校准矩阵具有某种受限形式,要么通过设置或等同某些元素,要么假设这些元素不会随时间变化。尽管哈特利和齐瑟曼(2004);穆恩斯、范古尔和维尔高文(2010)讨论的大多数技术需要三个或更多的帧,在本节中我们介绍一种简单的方法,可以从两个图像中恢复焦距(f0,f1)。
在两帧重建中,基本矩阵F(Hartley和Zisserman,2004年,第472页)。
为了实现这一目标,我们假设相机的偏斜度为零,已知的纵横比(通常设为1),以及已知的图像中心,如公式(2.59)所示。这个假设在实践中有多合理?答案是“视情况而定”。
如果需要绝对的测量精度,如摄影测量应用中那样,必须使用第11.1节中的某项技术预先校准相机,并利用地面控制点来确定重建。相反,如果我们只是希望为可视化或基于图像的渲染应用重建世界,例如斯纳维利、塞茨和舍利斯基(2006)提出的“照片旅游”系统,这种假设在实际操作中是相当合理的。
如今大多数相机的像素呈方形,图像中心位于画面中央附近,由于径向畸变(第11.1.4节),这些相机更可能偏离简单的相机模型,因此应尽可能进行补偿。最大的问题出现在图像被裁剪偏移中心时,此时图像中心将不再居中;或者当拍摄的是不同视角的照片时,就需要使用通用相机矩阵。17
考虑到这些注意事项,基于克鲁帕方程的两帧焦距估计算法(由哈特利和齐瑟曼于2004年提出,第456页)的具体步骤如下。取基础矩阵F(11.50)的左奇异向量{u0,u1,v0,v1 }及其对应的奇异值{σ0,σ 1 },并形成以下方程组:
(11.56)
两个矩阵在哪里
Dj = KjK = diag
eij0(f) = uD0 uj = aij + bij f , (11.58)
eij1(f) = σi σj vD1 vj = cij + dij f. (11.59)
请注意,每一个都是f或f的仿射(线性加常数)函数。因此,我们可以
将这些方程交叉相乘,得到关于f的二次方程,可以很容易地得到
在“照片旅游”中,我们的系统注册了巴黎圣母院外的信息标志的照片和大教堂的真实照片。
已解决。(另见Bougnoux(1998)和Kanatani与Matsunaga(2000)的其他表述。)
另一种解决方案是观察到我们有一组由未知标量λ相关的三个方程,即,
eij0(f) = λeij1(f) (11.60)
(Richard Hartley,个人交流,2009年7月)。这些都可以很容易地解决,得到
(f;λf;λ)因此(f0;f1)。
这种方法在实际应用中效果如何?存在某些退化配置,例如没有旋转或光轴相交时,该方法根本不起作用。(在这种情况下,可以通过改变相机的焦距来获得更深或更浅的重建,这是浮雕模糊的一个例子(第11.4.5节)。)哈特利和齐瑟曼(2004)建议使用基于三重技术的方法。
或者更多的帧。但是,如果您发现两个图像,它们的估计值为(f;λf;λ)
条件良好时,可以用来初始化所有参数的更完整的束调整(第11.4.2节)。另一种方法,在如照片旅游系统中常用,是使用相机EXIF标签或通用默认值来初始化焦距估计,并在束调整过程中对其进行优化。
基本的两帧结构从运动中的一种有趣的应用是视图变形(也称为视图插值,参见第14.1节),它可以用于从3D场景的一个视图生成另一个视图的平滑3D动画(Chen和Williams1993;Seitz和Dyer 1996)。
要实现这样的过渡,首先需要平滑地插值相机矩阵,即相机的位置、方向和焦距。虽然可以使用简单的线性插值(将旋转表示为四元数(第2.1.3节)),但通过缓入缓出相机参数,例如使用升余弦函数,以及沿更圆的轨迹移动相机(Snavely,Seitz,和Szeliski 2006),可以获得更加悦目的效果。
为了生成中间帧,要么需要建立完整的3D对应关系(第12.3节),要么为每个参考视图创建3D模型(代理)。第14.1节描述了几种广泛使用的方法来解决这个问题。最简单的方法之一是仅对每张图像中匹配的特征点进行三角化,例如使用德劳内三角化。当3D点重新投影到它们的中间视图时,可以使用仿射或投影映射将像素从原始源图像映射到新的视图(Szeliski和Shum 1997)。最终图像则通过线性混合合成。

图11.13使用因子分解法对旋转乒乓球进行三维重建(Tomasi
(Kanade1992)©1992 Springer:(a)叠加了跟踪特征的样本图像;(b)子采样特征运动流;(c)重建的3D模型的两个视图。
两个参考图像,与通常的变形(第3.6.3节)一样。
虽然两帧技术对于从立体图像对中重建稀疏几何结构和初始化更大规模的三维重建是有用的,但大多数应用可以从通常在场景的照片集合和视频中可用的大量图像中受益。
在本节中,我们简要回顾一种较老的技术,称为分解,它可以为短视频序列提供有用的解决方案,然后转向更常用的束调整方法,该方法使用非线性最小二乘法在一般相机配置下获得最优解。
11.4.1因式分解
在处理视频序列时,我们经常从视频中获得扩展特征轨迹(Section7.1.5)
使用一个叫做分解的过程可以恢复结构和运动。
考虑一个旋转的乒乓球产生的轨迹,它被标记了点以使其形状和运动更易辨认(图11.13)。我们很容易从轨迹的形状看出移动物体必须是一个球体,但是我们如何从数学上推断这一点呢?
结果表明,在下面讨论的正字法或相关模型下,形状和运动可以同时使用奇异值分解(Tomasi和
Kanade1992)。如何做到这一点的细节在Tomasi和Kanade的论文中有所介绍
(1992)以及本书第一版(Szeliski2010,第7.3节)。
一旦旋转矩阵和三维点位置被恢复,仍然存在一种浮雕式的不确定性,即我们无法确定物体是向左旋转还是向右旋转,或者其深度反转版本是否在相反方向移动。(这可以从经典的旋转内克立方体视觉错觉中看出。)额外的线索,如点的出现和消失,或透视效果,这些将在下文讨论,可以用来消除这种不确定性。
对于纯正字法以外的运动模型,例如比例正字法或准透视法,上述方法必须以适当的方式扩展。这些技术从基本原理推导相对简单;更多细节可以在扩展基本分解方法到这些更灵活模型的论文中找到(Poel- man和Kanade 1997)。原始分解算法的其他扩展包括多体刚体运动(Coste-ra和Kanade 1995)、分解的顺序更新(Morita和Kanade 1997)、添加直线和平面(Morris和Kanade 1998),以及重新缩放测量值以纳入个体位置不确定性(Anandan和Irani 2002)。
因子分解方法的一个缺点是需要完整的轨迹集,即每个点必须在每一帧中可见,才能使因子分解方法生效。Tomasi和Kanade(1992)通过首先将因子分解应用于较小且更密集的子集,然后利用已知的相机(运动)或点(结构)估计来推测额外的缺失值,从而逐步纳入更多特征和相机。Huynh、Hartley和Heyden(2003)将这种方法扩展到视图缺失数据作为异常值的特殊情况。Buchanan和Fitzgibbon(2005)开发了快速迭代算法,用于处理带有缺失数据的大矩阵因子分解。主成分分析(PCA)在处理缺失数据时的一般主题也出现在其他计算机视觉问题中(Shum、Ikeuchi和Reddy 1995;De la Torre和Black 2003;Gross、Matthews和Baker 2006;Torresani、Hertzmann和Bregler 2008;Vidal、Ma和Sastry 2016)。
视角与投影分解
常规分解的另一个缺点是无法处理透视相机。解决这一问题的一种方法是先进行初始仿射(例如正交)重建,然后通过迭代方式校正透视效果(Christy和Horaud 1996)。该算法通常在三到五次迭代中收敛,大部分时间用于奇异值分解计算。
另一种方法,不假设部分校准的相机(已知的im
(中心点、方像素和零偏斜)是执行完全投影分解(Sturm和Triggs1996;Triggs1996)。在这种情况下,将相机矩阵的第三行包含在测量矩阵中相当于将每个重建的测量值相乘。
xji = Mj pi的逆(投影)深度ηji = dj1 = 1/(Pj2pi),或者等效地,多-
将每个测量位置乘以其投影深度dji。在Sturm和Triggs(1996)的原始论文中,投影深度dji是从两帧重建中获得的,而在后来的工作中(Triggs 1996;Oliensis和Hartley 2007),它们被初始化为dji = 1,并在每次迭代后更新。Oliensis和Hartley(2007)提出了一种保证收敛到固定点的更新公式。这些作者都没有建议实际估计Pj的第三行作为投影深度计算的一部分。无论如何,当完全投影重建比部分校准重建更优时,尤其是在用于初始化所有参数的完整束调整时,这一点尚不清楚。
因子分解方法的一个吸引点在于它们提供了一种“封闭形式”(有时称为“线性”)的方法来初始化诸如束调整等迭代技术。另一种初始化技术是估计所有相机共有的平面对应的单应矩阵(Rother和Carlsson 2002)。在已校准的相机设置中,这可以对应于估计所有相机的一致旋转,例如使用匹配的消失点(Antone和Teller 2002)。一旦这些参数被恢复,就可以通过求解线性系统来获得相机位置(Antone和Teller 2002;Rother和Carlsson 2002;Rother 2003)。
正如我们之前多次提到的,恢复结构和运动最准确的方法是进行测量(重投影)误差的稳健非线性最小化,这在摄影测量学(以及现在的计算机视觉)领域通常被称为束调整。Triggs、McLauchlan等人(1999)对此主题提供了极好的概述,包括其历史发展、摄影测量文献的引用(Slama 1980;Atkinson 1996;Kraus 1997),以及度量模棱两可的微妙问题。这一主题也在多视图几何的教科书和综述中得到了深入探讨(Faugeras和Luong 2001;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。
在我们对束调整的讨论中,我们已经介绍了束调整的要素
推断姿态估计(第11.2.2节),即公式(11.14–11.20)和图11.7。

图11.14一组链式变换,用于通过一系列变换f(k)将3D点pi投影到2D测量值xij上,每个变换由其自身的参数集控制。虚线表示在反向传播过程中计算偏导数时的信息流。径向畸变函数的公式为fRD (x) =(1 + h1 r²+ h2 r⁴)x。
这些公式和完整的束调整之间的最大区别是,我们的特征位置测量xij现在不仅取决于点(轨迹)索引i,而且还取决于相机姿态索引j,
xij = f (pi, Rj, cj, Kj ), (11.61)
并且三维点位置pi也在同时更新。此外,通常会增加一个径向畸变参数估计阶段(2.78),
fRD (x) = (1 + h1 r2 + h2 r4 )x, (11.62)
如果所用摄像机未进行预校准,如图11.14所示。
虽然图11.14中的大多数框(变换)之前已经解释过(11.19),但最左边的框还没有。这个框执行预测和测量的二维位置ij Σij的稳健比较。更详细地说,这个操作可以写为
rij = ij - ij ,
(11.63)
sj = rΣi1 rij , (11.64)
eij = (sj ), (11.65)其中(r2)= P(r)。相应的雅可比矩阵(偏导数)可以写为
(11.66)
1 rij
. (11.67)

图11.15摄像机支架及其相关的变换链。(a)作为移动支架(机器人)
在世界中移动,它相对于时间t的世界的姿态由(R;c)捕捉。
每个摄像机相对于支架的姿态由(R;c)捕捉。(b)一个具有世界坐标系的三维点
坐标p首先转换为rig坐标p,然后通过其余的
如图11.14所示,为特定相机的链。
上述链式表示的优势不仅在于简化了偏导数和雅可比矩阵的计算,还能适应任何相机配置。例如,考虑图11.15a中展示的一对安装在机器人上的相机,该机器人正在世界中移动。通过将图11.14中最右侧的两个变换替换为图11.15b所示的变换,我们可以同时恢复机器人在每个时间点的位置以及每台相机相对于整个装置的校准,此外还能获得世界的三维结构。
大规模束调整问题,例如从数千张互联网照片中重建三维场景(Snavely,Seitz和Szeliski 2008b;Agarwal,Furukawa等2010,2011;Snavely,Simon等2010),可能需要解决包含数百万测量值(特征匹配)和数万个未知参数(三维点位置和相机姿态)的非线性最小二乘问题。如果不加以谨慎处理,这类问题可能会导致严重的后果。

图11.16 (a)玩具结构运动问题的二部图及其相关的雅可比矩阵J和(c)海森矩阵A。数字表示三维点,字母表示相机。虚线弧和浅蓝色方块表示当结构(点)变量被消除时发生的填充。
问题可能变得难以解决,因为稠密最小二乘问题的(直接)解与未知数的数量呈立方关系。
幸运的是,运动结构问题是一个关于结构和运动的二元问题。给定图像中的每个特征点xij都依赖于一个三维点位置pi和一个三维相机姿态(Rj;cj)。这在图11.16a中有所说明,其中每个圆圈(1-9)表示一个三维点,每个方块(A-D)表示一个相机,线条(边)表示哪些点在哪些相机中可见(二维特征)。如果所有点的值已知或固定,则所有相机的方程变得独立,反之亦然。
如果我们先在海森矩阵A(以及右侧向量b)中排列结构变量,再排列运动变量,则得到如图11.16c.19所示的海森结构。当使用稀疏乔列斯基分解求解此类系统时(见附录A.4)(Bj rck1996;Golub和Van Loan1996),填充会在较小的运动海森矩阵Acc中发生(Szeliski
和Kang1994;Triggs、McLauchlan等人1999;Hartley和Zisserman2004;Lourakis和Argyros2009;Engels、Stew nius和Nist r2006)。最近的一些论文(Byr d和A˚str m2009;Jeong、Nist r等人
2010;Agarwal、Snavely等人2010;Jeong
、Nist r等人2012)探讨
了使用迭代(共轭梯度)技术解决束调整问题的
方法。其他论文则研究了并行多核算法的使用(Wu、Agarwal等人2011)。
19当摄像机数量少于3D点时,这种排序方式是可取的,这是通常的情况。例外情况是,我们通过许多视频帧跟踪少量点,在这种情况下,应该反向这种排序方式。
更详细地说,使用Schur补计算降阶运动Hessian矩阵,
= ACC
- AAP-Apc; (11.68)
其中,APP是点(结构)海森矩阵(图11.16c的左上角块),APC是点-相机海森矩阵(右上角块),而ACC和A分别是点变量消除前后
的运动海森矩阵(图11.16c的右下角块)。请注意,如果两个相机看到相同的三维点,则A在这两个相机之间
有一个非零元素。这在图11.16a中用虚线弧表示,在图11.16c中用浅蓝色方块表示。
在重建算法中,如果存在全局参数,例如所有相机共有的相机内参,或者如图11.15所示的相机支架校准参数,则应将其放在最后(放置在A的右边缘和底部边缘),以减少填充。
恩格斯、斯图尼乌斯和尼斯特(
2006)提供了一种稀疏束调整的优良配方,包括初始化迭代所需的所有步骤,以及在实时设置中使用固定数量的后向帧系统的典型计算时间。他们还建议使用齐次坐标来表示结构参数pi,这是一个好主意,因为它可以避免接近无穷远点的数值不稳定问题。
束调整现在是大多数基于运动构建结构问题的标准方法,常用于处理包含数百张弱校准图像和数万个点的问题。(更大规模的问题通常在摄影测量和航空影像中解决,但这些问题通常经过精心校准,并利用了地面控制点。)然而,随着问题规模的增大,每次迭代重新求解完整的束调整变得不切实际。
处理这一问题的一种方法是使用增量算法,随着时间的推移逐步增加新的摄像头。(如果数据来自视频摄像机或移动车辆,则这种方法尤为适用(Nist r、Naroditsky和Bergen 2006;Pollefeys、Nist r等2008)。)可以使用卡尔曼滤波器
来随着新信息的获取而
逐步更新估计值。然而,这种顺序更新仅在统计上对线性最小二乘问题是最优的。
对于非线性问题,如运动中的结构问题,需要使用扩展卡尔曼滤波器(Gelb1974;Vi ville和Faugeras1990)。为了克服这一限制,可以对数据进行多次处理(Azarbayejani和Pentland1995)。由于点会从视图
中消失(旧相机变得无关紧要),可以使用可变状态维度滤波器(VSDF)来调整随时间变化的状态变量集,例如,仅保留最近k帧中看到的相机和点轨迹(McLauchlan2000)。一种更灵活的方法是使用
固定数量的帧用于通过点和相机向后传播校正,直到参数变化低于阈值(Steedly和Essa 2001)。这些技术的变体,包括使用固定窗口进行束调整的方法(Engels、Stew nius和Nist r 2006)或选择关键帧进行完整的束调整(Klein和Murray 2008),现在常用于同时定位与建图(SLAM)和增强现实
应用中,详见第11.5节。
当需要最高精度时,仍然最好对所有帧进行全面束调整。为了控制由此产生的计算复杂度,一种方法是将帧子集锁定为局部刚性配置,并优化这些簇的相对位置(Steedly,Essa和Dellaert 2003)。另一种方法是从较小数量的帧中选择一组骨架集,该集合仍能覆盖整个数据集并产生具有相当精度的重建(Snavely,Seitz和Szeliski 2008b)。我们在第11.4.6节中更详细地描述了后一种技术,在那里我们讨论了结构从运动到大型图像集的应用。关于高效解决大型结构从运动和SLAM系统的其他技术,可以在Dellaert和Kaess(2017);Dellaert(2021)的综述中找到。
虽然束调整和其他稳健的非线性最小二乘技术是大多数结构从运动问题的首选方法,但它们存在初始化问题,即如果初始条件不够接近全局最优解,可能会陷入局部能量最小值。许多系统试图通过在早期重建时保守处理以及选择哪些相机和点加入解决方案来减轻这一问题(第11.4.6节)。然而,另一种替代方案是重新定义问题,使用支持计算全局最优解的范数。
卡赫和哈特利(2008)描述了在几何重建问题中使用L∞范数的技术。这类范数的优势在于,可以利用二阶锥规划(SOCP)高效计算全局最优解。然而,L∞范数对异常值特别敏感,因此在使用前必须结合良好的异常值剔除技术。
大量高质量的开源束调整包已经开发出来,包括Ceres求解器、多核束调整(吴、阿加瓦尔等人,2011年)、基于稀疏莱文堡-马夸特法的非线性最小二乘优化器和束调整器,以及OpenSfM。您可以在附录C.2中找到更多关于开源软件的指南,以及对开源和商业摄影测量软件的综述。
结构从运动的一个最精妙的应用是估计视频或电影摄像机的三维运动,以及三维场景的几何形状,以便将三维图形或计算机生成图像(CGI)叠加到场景上。在视觉效果行业中,这被称为匹配移动问题(Roble1999),因为用于渲染图形的合成三维摄像机的运动必须与现实世界的摄像机运动相匹配。对于非常小的运动,或者仅涉及纯旋转的运动,一两个跟踪点就足以计算所需的视觉运动。对于在三维空间中移动的平面表面,则需要四个点来计算单应性,然后可以使用该单应性插入平面覆盖层,例如,在体育赛事期间替换广告牌的内容。
这个问题的一般版本需要估计完整的三维相机姿态以及镜头的焦距(变焦)和可能的径向畸变参数(Roble1999)。当场景的三维结构事先已知时,可以使用诸如视图相关性(Bogart1991)或透镜内相机控制(Gleicher和Witkin1992)等姿态估计技术,如Section11.4.4所述。
对于更复杂的场景,通常最好使用结构从运动技术同时恢复相机运动和三维结构。使用这些技术的关键在于,为了防止合成图形与实际场景之间出现任何可见的抖动,特征必须被跟踪到非常高的精度,并且在插入位置附近必须有足够的特征轨迹。当今一些最知名的匹配移动软件包,如2d3公司的boujou软件包,该软件包于2002年获得艾美奖,起源于计算机视觉社区中的结构从运动研究(Fitzgibbon和Zisserman 1998)。
因为运动结构涉及估计大量高度耦合的参数,通常没有已知的“真实”成分,所以运动结构算法产生的估计结果往往表现出大量的不确定性(Szeliski和Kang 1997;Wilson和Wehrwein 2020)。一个例子是经典的浮雕模糊性问题,
使得很难同时估计场景的三维深度和相机运动量(Oliensis2005).26
如前所述,仅凭单目视觉测量无法恢复重建场景的独特坐标系和比例。(当使用立体相机时,如果我们知道相机之间的距离(基线),则可以恢复比例。)这种七自由度(坐标系和比例)的量纲不确定性使得计算与三维重建相关的协方差矩阵变得复杂(Triggs,McLauchlan等1999;Kanatani和Morris 2001)。一种简单的方法是忽略量纲自由度(不确定性),即丢弃信息矩阵(逆协方差)的七个最小特征值,这些值在噪声缩放下等同于问题的海森矩阵A(见第8.1.4节和附录B.6)。完成这一步后,可以对所得矩阵求逆以获得参数协方差的估计。
斯泽利斯基和康(1997)利用这种方法来可视化典型结构从运动问题中最大的变化方向。不出所料,他们发现,在忽略规范自由度的情况下,对于从少量附近视角观察物体等问题,最大的不确定性在于三维结构的深度,而非相机运动的程度。27
也可以估计单个参数的局部或边缘不确定性,这相当于从完整的协方差矩阵中提取块子矩阵。在某些条件下,例如当相机姿态相对于3D点位置较为确定时,这种不确定性估计是有意义的。然而,在许多情况下,单个不确定性度量可能会掩盖重建误差的相关程度,因此查看最大联合变异的前几个模式是有帮助的。
另一种方式是,规范不确定性会影响运动结构,特别是束调整,使系统中的海森矩阵A秩亏,因此无法求逆。为了缓解这一问题,已经提出了一些技术(Triggs,McLauchlan等,1999;Bartoli,2003)。然而,在实际应用中,通常的做法是简单地将Hessian对角线λdiag(A)的小部分加到Hessian矩阵A本身上,这在Levenberg-Marquardt非线性最小二乘算法中有所体现(附录A.3)。
26浮雕是指一种雕塑形式,其中物体通常位于装饰性的浮雕上,雕刻得比实际占据的空间要浅。当从上方被阳光照亮时,由于相对深度与光源角度之间的模糊性(第13.1.1节),它们看起来具有真正的三维深度。
27一种减少此类模糊性的有效方法是使用广角摄像机(Antone和Teller 2002;Levin和Szeliski 2006)。

图11.17增量结构从运动中获得(Snavely、Seitz和Szeliski2006)©2006 ACM。从特雷维喷泉的初始两帧重建开始,使用姿态估计添加图像批次,并使用束调整优化它们的位置(以及3D模型)。
结构从运动最广泛的应用是在视频序列和图像集合中重建三维物体和场景(Pollefeys和Van Gool 2002)。过去二十年间,自动执行此任务的技术出现了爆炸式增长,无需任何手动对应或预先勘测的地面控制点。许多这些技术假设场景是由同一台相机拍摄的,因此所有图像都具有相同的内参(Fitzgibbon和Zisserman 1998;Koch、Pollefeys和Van Gool 2000;Schaffalitzky和Zisserman 2002;Tuytelaars和Van Gool 2004;Pollefeys、Nist等2008;Moons、Van Gool和Vergauwen 2010)。许多这些技术利用稀疏特征匹配和结构从运动计算的结果,然后使用多视图立体技术计算密集
的三维表面模型(第12.7节)(Koch、Pollefeys和Van Gool 2000;Pollefeys和Van Gool 2002;Pollefeys、Nist等2008;Moons、Van Gool和Vergauwen 2010;Schnberger、Zheng等2016)。
在这个领域的一项令人兴奋的创新是将运动结构和多视图立体技术应用于从互联网获取的数千张图像,而这些照片拍摄相机的信息知之甚少(Snavely,Seitz和Szeliski 2008a)。在开始运动结构计算之前,首先需要建立不同图像对之间的稀疏对应关系,然后将这些对应关系链接成特征轨迹,即关联单个二维图像特征与全局三维点。由于所有图像对的O(N^2)比较过程可能非常缓慢,因此识别社区开发了多种技术来加快这一过程(第7.1.4节)(Nist和Stew nius 2006;Philbin、Chum等2008;Li、Wu等2008;Chum、Philbin和Zisserman 2008;Chum和Matas 2010a;Arandjelovi和Zisserman 2012)。

图11.18由斯纳维利、塞茨和塞尔利斯基(2006)开发的增量结构从运动算法生成的3D重建©2006 ACM:特拉法加广场的(a)相机和点云;长城上的(b)相机和点叠加在图像上;布拉格老城广场的(c)俯视图,该重建与航拍照片注册。
开始重建过程时,选择一对好的图像至关重要,这些图像不仅包含大量一致的匹配点(以降低错误对应的可能性),还应有显著的面外视差,以确保能够获得稳定的重建结果(Snavely,Seitz和Szeliski 2006)。与照片相关的EXIF标签可用于获取相机焦距的良好初始估计,尽管这并非总是严格必要,因为这些参数会在束调整过程中重新调整。
一旦初始对被重建,就可以估计出看到足够多结果3D点的相机姿态(第11.2节),并使用完整的相机和特征对应关系进行另一轮束调整。图11.17展示了增量束调整算法的进展过程,在每一轮束调整后都会增加一组相机,而图11.18则展示了一些额外的结果。这种种子和生长方法的替代方案是首先重建图像三元组,然后将它们层次化合并成更大的集合(Fitzgibbon和Zisserman 1998)。
不幸的是,随着增量结构从运动算法不断增加更多的摄像头和点,它可能会变得极其缓慢。直接求解相机姿态更新的密集O(N)方程组可能需要O(N^3)的时间;而结构从运动问题很少是密集的,像城市广场这样的场景具有较高的比例。
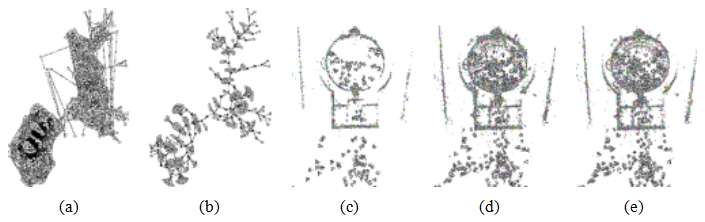
图11.19使用骨架集进行大规模结构运动重建(Snavely,Seitz和Szeliski 2008b)©2008 IEEE:784张图像的原始匹配图;(b)包含101张图像的骨架集;(c)从骨架集中重建的场景(万神殿)俯视图;(d)添加剩余图像后通过姿态估计重建的结果;(e)最终束调整重建,几乎完全相同。
相机识别出共同点。每次增加几台相机后重新运行束调整算法,会导致运行时间随着数据集中图像数量的增加而呈四次方增长。解决这一问题的一种方法是选择较少的图像进行原始场景重建,并在最后再加入剩余的图像。
斯纳维利、塞茨和谢利斯基(2008b)开发了一种算法,用于计算这样的图像骨架集,该算法保证生成的重建误差在最优重建精度的有界因子内。他们的算法首先评估所有重叠图像之间的两两不确定性(位置协方差),然后将这些不确定性串联起来,以估计任意远距离对的相对不确定性的下限。骨架集构建的方式是,任意一对之间的最大不确定性增长不超过一个常数因子。图11.19展示了为罗马万神殿的784张图像计算出的骨架集的一个例子。如你所见,尽管骨架集仅包含原始图像的一小部分,但骨架集和完整的束调整重建的形状几乎无法区分。
自斯纳维利、塞茨和舍利斯基(2008a,b)首次发表大规模互联网照片重建研究以来,大量后续论文探索了更大的数据集和更高效的算法(阿加瓦尔、古川等人2010,2011;弗拉姆、菲特-格奥格尔等人2010;吴2013;海因利、施恩伯格等人2015;施恩伯格和弗拉姆2016)。其中,COLMAP开源结构从运动和多
视图立体系统目前是最广泛
使用的之一,因为它能够重建极其庞大的场景,

图11.20大规模重建,使用COLMAP结构从运动和多视图立体系统创建:从21K构建的罗马市中心(a)稀疏模型
照片(Sch nberger和Frahm2016)©2016 IEEE;多个地标的(b)密集模型
采用MVS管道生产(Sch nberger,Zheng等人,2016)©2016 Springer。
例如图11.20所示(Sch nberger和Frahm2016).29
从大量非结构化图像集合中自动重建三维模型的能力,也揭示了传统运动结构算法中存在的细微问题,包括需要处理重复和相似的结构(吴、弗拉姆和波莱菲斯2010;罗伯茨、辛哈等人2011;威尔逊和斯纳维利2013;海因利、邓恩和弗拉姆2014),以及动态视觉对象如人物(吉、邓恩和弗拉姆2014;郑、王等人2014)。这一能力还开启了多种附加应用,包括自动查找和标注感兴趣的位置和区域(西蒙、斯纳维利和塞茨2007;西蒙和塞茨2008;加米特、博萨德等人2009),以及对大型图像集合进行聚类以便自动标注(李、吴等人2008;夸克、莱贝和范古尔2008)。关于基于图像渲染的一些其他应用将在第14.1.2节中详细讨论。
尽管增量束调整算法仍然是大规模重建中最常用的方法(Sch nberger和Frahm2016),但它们可能相当慢,因为

图11.21 Sinha、Steedly和Szeliski(2010)提出的全局运动结构流水线©2010斯普林格。首先使用消失点和基于特征的成对旋转估计来确定一组全局一致的方向(旋转)。然后通过单次线性最小二乘法最小化,估计所有成对重建的尺度以及相机中心位置。
需要连续解决越来越大的优化问题。在特征对应关系建立后,一种替代迭代增长解决方案的方法是在一个全局步骤中求解所有结构和运动未知数。
一种方法是建立一个线性方程组,将所有相机中心以及三维点、线和平面方程与已知的二维特征或线条位置联系起来(Kaucic,Hartley和Dano 2001;Rother 2003)。然而,这些方法需要参考平面(例如,建筑物墙壁)在所有图像中都可见且匹配,并且对远距离点敏感,这些点必须首先被剔除。尽管这些方法理论上很有吸引力,但并未广泛使用。
第二种方法由戈文杜(2001)首次提出,首先使用第11.3.3节讨论的技术计算成对欧几里得结构和运动重建。然后利用成对旋转估计来计算每个相机的全局一致方向估计,这一过程称为旋转平均(戈文杜2001;马蒂内克和帕伊德拉2007;查特吉和戈文杜2013;哈特利、特鲁姆夫等人2013;德拉尔特、罗森等人2020)。最后一步是通过将每个局部相机平移缩放至全局坐标系中,确定相机位置(戈文杜2001,2004;马蒂内克和帕伊德拉2007;辛哈、斯特迪和舍利斯基2010)。在机器人(SLAM)领域,这最后一步被称为姿态图优化(卡尔洛内、特隆等人2015)。
图11.21展示了一个更近期的实现该概念的流水线,包括初始特征点提取、匹配和双视图重建,随后是全局旋转估计,最后求解相机中心。辛哈、斯特迪和斯泽利斯基(2010)开发的流水线还匹配了消失点,当这些消失点可以找到时,
以消除全球方向估计中的旋转漂移。
虽然有几种替代算法可以估计全局旋转,但估计相机中心的算法种类更多。在对所有相机进行全局旋转估计后,我们可以计算全局定向的局部平移
在每个重构的对ij中,用ij表示这个方向。基本关系
未知摄像机中心{ci }和平移方向之间的关系可以表示为
cj - ci = sij ij (11.69)
或
ij × (cj - ci) = 0 (11.70)
(Govindu2001)。第一组方程可以求解以获得相机中心{ci }和尺度变量sij,而第二组方程则直接生成相机位置。除了具有齐次性(仅知其比例)外,相机中心还具有平移自由度,即它们都可以被平移(但在运动结构中这总是成立的)。
因为这些方程最小化了局部平移方向与全局相机中心差异之间的代数对齐,所以它们无法正确地权衡不同基线的重建结果。为了纠正这一问题,已经提出了几种替代方案(Govindu 2004;Sinha、Stedly和Szeliski 2010;Jiang、Cui和Tan 2013;Moulon、Monasse和
Marlet2013;Wilson和Snavely2014;Cui和Tan2015;zyes¸il和Singer2015;Holyn-
ski、Geraghty等人,2020年)。其中一些技术也无法处理共线相机,正如最初的形式一样,以及一些更近期的技术,我们可以沿着共线段移动相机,仍然满足方向约束。
对于在大型区域如广场上拍摄的社区照片集,这并不是一个关键问题(Wilson和Snavely 2014)。然而,在从视频重建或在建筑物内行走时,共线相机问题确实是一个实际问题。Sinha、Steedy和Szeliski(2010)通过估计共享同一相机的两两重建之间的相对尺度来解决这一问题,然后利用这些相对尺度约束所有全局尺度。
包含这些全局技术的一些开源结构化运动管道有Theia32(Sweeney,Hollerer和Turk2015)和OpenMVG33 (Moulon,Monasse

图11.22玩具房屋的两个图像及其匹配的3D线段(Schmid和Zisserman1997)©1997 Springer。
最通用的运动结构算法在重建对象或场景时不会做出任何先验假设。然而,在许多情况下,场景中包含高层次的几何基元,如直线和平面。这些基元可以提供与兴趣点互补的信息,同时也是三维建模和可视化的重要构建模块。此外,这些基元通常以特定关系排列,即许多直线和平面要么平行,要么正交(周、古川和马2019;周、古川等2020)。这一点在建筑场景和模型中尤为明显,我们将在第13.6.1节中详细讨论。
有时,与其利用场景结构的规律性,不如采用受限运动模型。例如,如果感兴趣的对象是在转盘上旋转(Szeliski1991b),即绕一个固定但未知的轴旋转,可以使用专门的技术来恢复这种运动(Fitzgibbon,Cross,和Zisserman1998)。在其他情况下,摄像机本身可能围绕某个旋转中心沿固定弧线移动(Shum和He1999)。专门的捕捉装置,如移动立体相机架或配备多个固定摄像头的移动车辆,也可以利用单个摄像头相对于捕捉装置(大多)固定的已知信息,如图11.15.34所示。
众所周知,即使相机已经校准,仅凭线对匹配也无法恢复成对的极线几何。要理解这一点,可以想象将每张图像中的线条投影到空间中的三维平面上。你可以随意移动两台相机,仍然能够获得有效的三维线条重建。
当线在三个或更多视图中可见时,可以使用三焦张量将线从一对图像转移到另一对图像(Hartley和Zisserman2004)。也可以仅基于线匹配来计算三焦张量。
施密德和齐瑟曼(1997)描述了一种广泛使用的二维线匹配技术,该技术基于沿共同线段交点的所有像素处的15×15像素相关性得分的平均值。在他们的系统中,假设极线几何已知,例如通过点匹配计算得出。对于宽基线,使用所有可能的通过三维线的平面对应的单应性来扭曲像素,并采用最大相关性得分。对于三张图像的组合,使用三焦张量验证线条是否在几何上对应,然后再评估线段之间的相关性。图11.22展示了他们系统的使用结果。
Bartoli和Sturm(2003)描述了一个完整的系统,用于将从手动线对应关系计算出的三个视图关系(三焦张量)扩展到一个完整的束调整
所有的线和摄像机参数。他们方法的关键是使用Plcker坐标-
参数化线段(2.12),以直接最小化重投影误差。还可以通过端点表示三维线段,并测量每个图像中检测到的二维线段的垂直重投影误差,或使用与线段方向对齐的拉长不确定性椭圆来测量二维误差(Szeliski和Kang 1994)。
贝、法拉利和范古尔(2005)没有重建三维线,而是使用RANSAC将线段聚类为可能共面的子集。随机选取四条线来计算同态矩阵,然后通过评估基于颜色直方图的相关性得分来验证这些及其他合理的线段匹配。属于同一平面的线段的二维交点随后被用作虚拟测量,以估计极线几何,这比直接使用同态矩阵更为准确。
将线条按共面子集分组的另一种方法是根据平行性进行分组。当三条或更多条二维线共享一个共同的消失点时,它们在三维空间中很可能是平行的。通过在图像中找到多个消失点(第7.4.3节),并建立不同图像中这些消失点之间的对应关系,可以直接估计各图像之间的相对旋转(以及通常相机内参)(第11.1.1节)。寻找一组正交的消失点并利用这些消失点来确定全局方向,通常被称为曼哈顿世界假设(Coughlan和Yuille 1999)。Schindler和Dellaert(2004)提出了一种广义版本,其中街道可以在非正交角度相交,称为亚特兰大世界。
舒姆、韩和斯泽利斯基(1998)描述了一种三维建模系统,该系统从多张图像构建校准全景图(第11.4.2节),然后让用户在图像中绘制垂直线和水平线以界定平面区域的边界。这些线条用于确定每个全景图的绝对旋转角度,随后与推断出的顶点和平面一起,用于构建三维结构,可以从一张或多张图像中按比例恢复(图13.20)。
Werner和Zisserman(2002)提出了一种完全自动化的基于线的运动结构方法。在他们的系统中,首先找到线条并根据每张图像中的共同消失点进行分组(第7.4.3节)。然后利用这些消失点来校准相机,即执行“度量升级”(第11.1.1节)。接着使用外观特征(Schmid和Zisserman 1997)和三焦张量匹配与共同消失点对应的线条。这些线条随后用于推断场景中的平面和块状结构模型,具体细节见第13.6.1节。最近的研究还使用深度神经网络从一张或多张图像构建3D线框模型。
基于飞机的技术
在平面结构丰富的场景中,例如建筑领域,可以直接估计不同平面之间的单应性,使用基于特征或基于强度的方法。原则上,这些信息可以同时推断相机姿态和平面方程,即计算基于平面的运动结构。
Luong和Faugeras(1996)展示了如何通过代数运算和最小二乘法直接从两个或多个同态计算出一个基本矩阵。不幸的是,这种方法通常表现不佳,因为代数误差并不对应于有意义的重投影误差(Szeliski和Torr1998)。
更好的方法是在计算每个单应矩阵的区域中虚幻虚拟点对应关系,并将其输入到标准运动算法(Szeliski和Torr 1998)中。更优的方法是使用带有显式平面方程的全束调整,并施加额外约束,以确保重建的共面特征精确位于其对应的平面上。(一种合理的方法是在每个平面上建立一个坐标系,例如在其中一个特征点处,并对其他点使用二维平面内参数化。)Shum、Han和Szeliski(1998)开发的系统展示了这种方法的一个例子,其中场景中各平面的线方向和法向量由用户预先指定。在最近的研究中,Micusik和Wildenauer(2017)在束调整公式中使用平面作为附加约束。其他近期论文则利用线条和/或平面的组合来减少漂移。

图11.23在同时定位和制图(SLAM)中,系统同时估计机器人及其附近地标的位置(Durrant-Whyte和Bailey 2006)©2006 IEEE。
3D重建包括(Zhou,Zou等人,2015),Li,Yao等人(2018),Yang和Scherer
(2019年),和Holynski,Geraghty等人(2020年)。
虽然计算机视觉界自20世纪80年代初(Longuet-Higgins1981)以来一直在研究运动结构,即从多张图像和视频中重建稀疏的3D模型,但移动机器人领域却在平行地研究如何从移动机器人自动构建3D地图。在机器人学中,这一问题被表述为同时估计3D机器人和地标姿态(图11.23),并被称为概率建图(Thrun,Burgard,和Fox2005)和同时定位与建图(SLAM)(Durrant-Whyte和Bailey2006;Bailey和Durrant-Whyte 2006;Cadena,Carlone等人2016)。在计算机视觉界,这一问题最初被称为视觉里程计(Levin和Szeliski2004;Nist r,Naroditsky和Bergen 2006;Maimone,Cheng和Matthies2007),尽管现在通常该术语仅用于不涉及全局地图构建和环闭合的短程运动估计(Cadena,Carlone等人2016)。
早期版本的此类算法使用了超声波、激光等测距技术

2014)©2014 Springer,显示前端,它执行跟踪、数据关联和局部3D姿态和结构(深度图)更新,以及后端,它执行全局地图优化。
使用测距仪或立体匹配来估计局部三维几何,然后可以将其融合成三维模型。较新的技术可以通过单目相机的视觉特征跟踪来完成相同的任务(Davison,Reid等,2007)。关于这一主题的良好入门教程可以在Durrant-Whyte和Bailey(2006)以及Bailey和Durrant-Whyte(2006)中找到,而更全面的技术综述则见于Fuentes-Pacheco、Ruiz-Ascencio和Rendn-Mancha(2015)以及Cadenas、Carlone等(2016)。
SLAM在两个基本方面与束调整不同。首先,它允许使用多种传感设备,而不仅仅是局限于跟踪或匹配特征点。其次,它在线解决定位问题,即在提供当前传感器姿态时几乎没有延迟。这使得它成为时间关键的机器人应用如自主导航(第11.5.1节)和实时增强现实(第11.5.2节)的首选方法。
SLAM中的一些重要里程碑包括:
单目相机上的SLAM应用(MonoSLAM)(Davison,Reid等人,2007年);
并行跟踪和映射(PTAM)(Klein和Murray2007),将前端(跟踪)和后端(映射)过程(图11.24)拆分为两个以不同速率运行的独立线程(图11.27),然后在照相手机上实现整个过程(Klein和Murray2009);
自适应相对束调整(Sibley、Mei等人,2009年,2010年),它保持了在不同关键帧上锚定的局部重建集合;
增量平滑和映射(iSAM)(Kaess、Ranganathan和Dellaert2008;Kaess、Johannsson等人2012)和其他因子图应用,以处理速度-精度延迟权衡(Dellaert和Kaess2017;Dellaert2021);
•密集跟踪和映射(DTAM)(Newcombe,Lovegrove和Davison2011),它估计并更新每一帧的密集深度映射;
ORB-SLAM(Mur-Artal,Montiel和Tardos2015)和ORB-SLAM2(Mur-Artal和Tard s2017),处理
单目、立体和RGB-D相机以及回环闭合;
SVO(半直接视觉里程计)(Forster,Zhang等人,2017),它结合了基于补丁的跟踪和经典束调整;
LSD-SLAM(大规模直接SLAM)(Engel、Sch ps和Cremers2014
)和DSO(直接稀疏里程计)(Engel、Koltun和Cremers2018),仅在梯度强度位置保留深度估计值(图11.24)。
BAD SLAM(束调整直接RGB-D SLAM)(Sch ps、Sattler和Pollefeys,2019a)。
许多系统都有开源实现。一些广泛使用的基准测试包括:RGB-D SLAM系统的基准测试(Sturm,Engelhard等,2012年),KITTI视觉里程计/ SLAM基准测试(Geiger,Lenz等,2013年),合成ICL-NUIM数据集(Handa,Whelan等,2014年),TUM单目视觉数据集(Engel,Usenko和Cremers,2016年),EuRoC MAV数据集(Burri,Nikolic等,2016年),ETH3D SLAM基准测试(Sch ps,Sattler和Pollefeys,2019a),以及GSLAM通用SLAM基准测试
(Zhao,Xu等,2019年)。
最近的SLAM趋势是与视觉惯性里程计(VIO)算法的集成(Mourikis和Roumeliotis 2007;Li和Mourikis 2013;Forster、Carlone等人2016),这些算法结合了高频惯性测量单元(IMU)测量数据和视觉轨迹,以消除低频漂移。由于IMU现在在手机和运动相机等消费设备中已十分普遍,因此VIO增强的SLAM系统成为了广泛使用的移动增强现实框架如ARKit和ARCore的基础(第11.5.2节)。开源VIO系统的数据集和评估可参见Schubert、Goll等人(2018)。

图11.25自动车辆:(a)斯坦福车(Moravec1983)©1983 IEEE;(b) Junior:斯坦福在城市挑战赛中的参赛作品(Montemerlo,Becker等人2008)©2008 Wiley;(c-d)CVPR 2019展览现场的自动驾驶汽车原型。
正如你从这个简要概述中可以看出,SLAM是一个极其丰富且迅速发展的研究领域,充满了挑战性的稳健优化和实时性能问题。一个很好的资源是KITTI视觉里程计/SLAM评估(Geiger,Lenz和Urtasun 2012)以及重新发布的文献列表,可以找到最近的论文和算法。
关于自动驾驶计算机视觉的调查论文(Janai,G ney等人,2020年,
第13.2节)。
自从人工智能和机器人技术的早期,计算机视觉就被用于
为灵巧机器人提供操作,为自主机器人提供导航(Janai,G ney
等,2020;Kubota2019)。一些最早的基于视觉的导航系统包括斯坦福车(图11.25a)和CMU漫游者(Moravec1980,1983)、Terregator (Wallace,Stentz等人,1985)和CMU Nablab (Thorpe,Hebert等人,1988),这些系统

图11.26全自动Skydio R1无人机在野外飞行©2019 Skydio:(a)多个输入图像和深度图;(b)完全集成的3D地图(Cross2019)。
最初只能每10秒前进4米(< 1英里/小时),这也是第一个使用神经网络进行驾驶的系统(Pomerleau1989)。
早期算法和技术迅速进步,迪克曼斯和米斯利维茨(1992)的VaMoRs系统运行着一个25赫兹的卡尔曼滤波循环,并在100 km/h的车道标记下表现出色。到2000年代中期,当DARPA推出其大挑战赛和城市挑战赛时,配备了测距激光雷达相机和立体相机的车辆能够穿越崎岖的户外地形,并以常规的人类驾驶速度导航城市街道(乌姆森、安哈特等人,2008;蒙特梅罗、贝克等人,2008)。这些系统促使谷歌和特斯拉等公司成立了工业研究项目,以及众多初创企业,其中许多企业在计算机视觉会议上展示他们的车辆(图11.25c-d)。
对自动驾驶汽车的计算机视觉技术进行全面的回顾
可以在Janai、G ney等人(2020)的调查中找到,该调查还附带了一个有用的在线版本
相关论文的可视化工具。40调查包括大量视觉算法和组件的章节,这些算法和组件用于自主导航,涵盖数据集和基准测试、传感器、物体检测与跟踪、分割、立体视觉、流场和场景流场、SLAM、场景理解以及自动驾驶行为的端到端学习。
除了轮式(和腿式)机器人和车辆的自主导航,com-

图11.27 3D增强现实:(a)达斯·维达和一群伊沃克人在一张桌面上展开激战,该桌面是通过实时关键帧结构从运动(Klein和Murray 2007)©2007 IEEE;(b)一个虚拟茶壶固定在现实世界的咖啡杯顶部,其姿态在每个时间帧中重新识别(Gordon和Lowe 2006)©2007斯普林格。
计算机视觉算法广泛应用于自主无人机的控制,既包括娱乐应用(Ackerman 2019)(图11.26),也包括无人机竞速(Jung,Hwang等2018;Kaufmann,Gehrig等2019)。Gareth Cross(2019)在ICRA 2019关于自主飞行中学习系统算法与架构的工作坊以及Pieter Abbeel(2019)高级机器人课程的第23讲中,详细介绍了Skydio的视觉自主导航方法,该课程还有许多其他有趣的相关讲座。
另一个密切相关应用是增强现实,其中3D物体实时插入视频流中,通常用于标注或帮助用户理解场景(Azuma,Bail- lot等2001;Feiner 2002;Billinghurst,Clark和Lee 2015)。传统系统需要事先了解被视觉跟踪的场景或物体(Rosten和Drum-mond 2005),而新系统则可以同时构建3D环境模型并进行跟踪,以便叠加图形(Reitmayr和Drummond 2006;Wagner,Reitmayr等2008)。
Klein和Murray(2007)描述了一个并行跟踪和映射(PTAM)系统,
同时对从视频中选择的关键帧进行完整的捆绑调整
一旦初步重建了3D场景,就会估计出一个主要平面(在这种情况下是桌面),然后虚拟插入3D动画角色。Klein和Murray(2008)扩展了该系统,通过增加边缘特征来处理更快的摄像机运动,即使兴趣点变得过于模糊,这些特征仍然可以被跟踪。他们还使用了一种直接的(基于强度的)旋转估计算法,以实现更快速的运动。
戈登和洛(2006)没有将整个场景建模为一个刚性参考框架,而是首先使用特征匹配和运动结构技术构建单个物体的三维模型。系统初始化后,对于每一帧新图像,他们通过三维实例识别算法找到该物体及其姿态,然后将其图形对象叠加到模型上,如图11.27b所示。
尽管可靠地跟踪此类物体和环境现在是一个已解决的问题,随着ARKit、ARCore和Spark AR等框架被广泛用于移动AR应用开发,确定哪些像素应该被前景场景元素遮挡(Chuang,Agarwala等人,2002;Wang和Cohen,2009)仍然是一个活跃的研究领域。
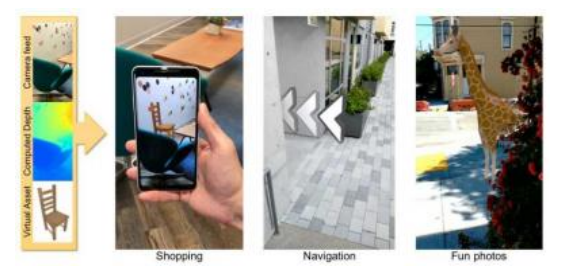
最近的一个例子是Valentin、Kowdle等人(2018)开发的智能手机AR系统,如图Figure11.28所示。该系统通过将当前帧与前一关键帧匹配,使用CRF后进行滤波步骤,生成半密集深度图。然后利用一种新颖的平面双边求解器将此地图插值至全分辨率,并用于遮挡效果。由于精确的逐像素深度是增强现实效果的关键组成部分,我们很可能会看到这一领域在主动和被动深度传感技术方面的快速进展。
相机校准最初在摄影测量学中被研究(Brown 1971;Slama 1980;Atkinson 1996;Kraus 1997),但在计算机视觉领域也得到了广泛研究(Tsai 1987;Gremban、Thorpe和Kanade 1988;Champleboux、Lavall e等1992b;Zhang 2000
;Grossberg和Nayar 2001)。通过矩形校准物体或建筑观察到的消失点常用于进行初步校准(Caprile和Torre 1990;Becker和Bove 1995;Liebowitz和Zisserman 1998;Cipolla、Drummond和Robertson 1999;Antone和Teller 2002;Criminisi、Reid和Zisserman 2000;Hartley和Zisserman 2004;Pflugfelder 2008)。不使用已知目标进行相机校准被称为
自校准在关于运动结构的教科书和调查中都有讨论(Faugeras、Luong和Maybank 1992;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。其中一种流行的技术子集使用纯旋转运动(Stein 1995;Hartley 1997b;Hartley、Hayman等2000;de Agapito、Hayman和Reid 2001;Kang和Weiss 1999;Shum和Szeliski 2000;Frahm和Koch 2003)。
注册3D点数据集的主题被称为绝对定向(Horn1987)和3D姿态估计(Lorusso,Eggert,和Fisher1995)。已经开发了多种技术,同时计算3D点对应及其相应的刚性变换(Besl和McKay1992;Zhang1994;Szeliski和Lavalle1996;Gold,Rangarajan等人1998;David,DeMenthon等人2004;Li和Hartley2007;Enqvist
,Joseph-Son和Kahl2009)。当只有2D观测时,已经开发了多种线性PnP(透视n点)算法(DeMenthon和Davis1995;Quan和Lan1999;Moreno-Noguer,Lepetit,和Fua2007;Terzakis和Lourakis2020)。最近的姿态估计方法使用深度网络(Arandjelovic,Gronat等人2016;Brachmann,Krull等人2017;Xiang,Schmidt等人2018;Oberweger,Rad,和Lepetit2018;Hu,Hugonot等人2019;Peng,Liu等人2019)。从RGB-D图像中估计姿态也非常活跃(Drost,Ulrich等人2010;Brachmann,Michel等人2016;Labb,Carpentier等人2020)。除了用于机器人任务的对象姿态识别外,姿态估计还广泛应用于位置识别(Sattler,Zhou等人2019
;Revaud,Weinzaepfel等人2019;Zhou,Sattler等人2019;Sarlin,DeTone等人2020;Luo,Zhou等人2020)。
关于运动结构的主题在多视图几何的书籍和综述文章中得到了广泛的讨论(Faugeras和Luong2001;Hartley和Zisserman2004;Moons,Van
Gool和Vergauwen2010)对zyes¸il、Voroninski的最新发展进行了调查
等人(2017)。对于两帧重建,哈特利(1997a)撰写了一篇关于“八点算法”的高度引用论文,该算法用于计算具有合理点归一化的本质或基本矩阵。当相机已校准时,可以结合RANSAC使用Nist r(2004)的五点算法,从最少数量的点中获得初始重建。当相机
未校准时,哈特利和齐瑟曼(2004)以及穆恩斯、范古尔和维尔高文(2010)的研究中提供了各种自校准技术。
特里格斯、麦克劳克兰等人(1999)提供了关于束调整的良好教程和综述,而劳拉基斯和阿尔吉罗斯(2009)以及恩格尔、斯图尼乌斯和尼斯特
(2006)则提供了实施和有效实践的建议。束调整也在多视图几何的教科书和综述中有所涉及(福加拉斯和隆2001;哈特利和齐瑟曼2004;穆恩斯、范古尔和维尔高文2010)。处理更大问题的技术由斯纳维利、塞茨和舍利斯基(2008b)、阿加瓦尔、塞茨等人(2009)、阿加瓦尔、塞茨等人(2010)、郑、尼斯特等人(2012)、吴(2013)、海因利、施纳伯格等
人(2015)、施纳伯格和弗拉姆(2016
)以及德拉特和凯斯(2017
)描述。虽然束调整通常被称为增量重建算法中的内循环(斯纳维利、塞茨和舍利斯基2006),但也有层次化(菲茨吉本和齐瑟曼1998;法伦泽纳、富西埃洛和格拉迪2009)和全局(罗瑟和卡尔松2002;马蒂内克和帕伊德拉2007;辛哈、斯特迪和舍利斯基2010;姜、崔和谭2013;莫隆、莫纳塞和马莱特2013;
Wilson和Snavely2014;Cui和Tan2015;zyes¸il和Singer2015;Holynski和Geraghty
(et al.2020)提出的初始化方法也是可能的,甚至可能是可取的。
在机器人领域,从移动机器人重建三维环境的技术被称为同时定位与建图(SLAM)(Thrun、Burgard和Fox 2005;Durrant-Whyte和Bailey 2006;Bailey和Durrant-Whyte 2006;Fuentes-Pacheco、Ruiz-Ascencio和Rendn-Mancha 2015;Cadena、Carlone等2016)。SLAM与束调整不同之处在于它允许使用
多种传感设备,并且能够在线解决定位问题。这使得它成为时间敏感型机器人的首选方法。
诸如自主导航(Janai,G ney等人,2020)和实时增强等应用
增强现实(Valentin,Kowdle等人,2018)。该领域的重点论文包括(Davison,Reid等人,2007;Klein和Murray,2007,2009;Newcombe,Lovegrove和Davison,2011;Kaess,Johannsson等人,2012;Engel
,Sch ps和Cremers,2014
;Mur-Artal和Tard s,2017;Forster,Zhang等人,2017;Dellaert和Kaess,2017;Engel,Koltun
和Cremers,2018;Sch ps,Sattler和Pollefeys,2019a)以及将SLAM与IMU结合以获得视觉惯性里程计(VIO)的论文(Mourikis和Roumeliotis,2007;Li和Mourikis,2013;Forster,Carlone等人,2016;Schubert,Goll等人,2018)。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








