【小呆的力学笔记】非线性有限元的初步认识【一】

0. 有限元方法的诞生

有限元方法是仿真模拟的重要方法，特别是在结构仿真中占据主导地位。从本质上来说，有限元方法和有限差分法等方法一样，都是一种求解物理方程的数值计算方法。计算机技术的迅猛发展使得数值仿真应用越来越广泛，有限元方法作为重要仿真工具内容也越来越丰富。
有限元方法从诞生之初就是为了 方便求解工程实际中的力学问题。1943年，Courant最先尝试使用三角形区域的多项式函数来求解结构静力学和振动问题。1956年，波音公司工程师Turner等人系统性的研究了离散结构的单元刚度问题，同时率先应用这种离散方法正确处理了飞机结构工程中的实际问题。这种离散方法的成功应用激起了工程师的热情，越来越多的工程师使用这种方法处理结构分析问题、流体力学问题、热传导问题等各种工程问题。1960年，波音工程师Clough第一次将这种方法命名为“有限元方法”。
在工程应用的同时，数学家通过研究发现通过能量泛函的极值问题或加权残差法能够导出有限元方法，坚实了有限元方法的数学基础。有限元方法最早应用和发展的主要集中在线性问题，特别对于结构分析来说，大部分的工程实际结构都满足小变形假设，材料也工作在弹性范围，那么线性有限元就能够解决大部分的问题。
随着有限元应用越来越广泛，更多的应用场景不能通过线性有限元来分析模拟了，例如：汽车的碰撞问题，航空发动机叶片脱落问题，金属薄板的加工成型问题，橡胶等超弹性材料的受力变形问题等等。这些问题都需要用非线性有限元的方法来仿真模拟。

1. 线性有限元的初步认识

学习非线性有限元之前先复习线性有限元理论。线性有限元分析的力学基础是弹性力学，来复习一下弹性力学知识。

1.1 弹性力学概述

1.1.1 弹性力学基本假设

在弹性力学研究的范围内，先得明确五个基本假设：
（1）连续性假设：该假设认为在弹性力学研究的范畴内，物体呈现其宏观尺度上的连续性特性，事实上，所有物质本质上均为不连续，但在远大于粒子尺度上（强力和弱力作用范围$10^{-15}$、$10^{-18}$，远小于弹性力学研究范围），物质往往表现出连续性的特性。
（2）均匀性假设：该假设认为物体内材料处处均匀。事实上，这往往是不成立的，学过金属材料的都知道，金属作为多晶体物质，内部存在大大小小各异的晶粒，晶粒间还有晶界，还有成形过程中的析出相等等，所以材料肯定不是处处均匀。不过在弹性力学研究的范畴内，材料往往可以处理成处处均匀，也不至于很大误差。
（3）各向同性假设：该假设认为物体内各点的材料各方向的力学特性相同。这对很多金属材料适用。弹性力学仅仅是为了简化研究对象，本质上各项异性不影响弹性力学的研究。
（4）线弹性假设：该假设认为在弹性力学研究中的物体材料变形和受到的外力呈线性关系。这是限定弹性力学适用范围的条件一。
（5）小变形假设：该假设认为在弹性力学研究中物体的变形比较小，转动更小，变形前后物体的几何形状、尺寸和位置不至于发生较大的变化。这是限定弹性力学适用范围的条件二。

1.1.2 平衡方程

此外，还需要引入微元体作为研究对象，三维的微元体见下图，微元体的各边长为dx、dy、dz，其中微元体表面的法向与坐标正方向一致的都用黑色箭头和黑色字体，表面的法向与坐标负方向一致的都用蓝色箭头和字体，微元体面上的应力按照如下的规则定义。

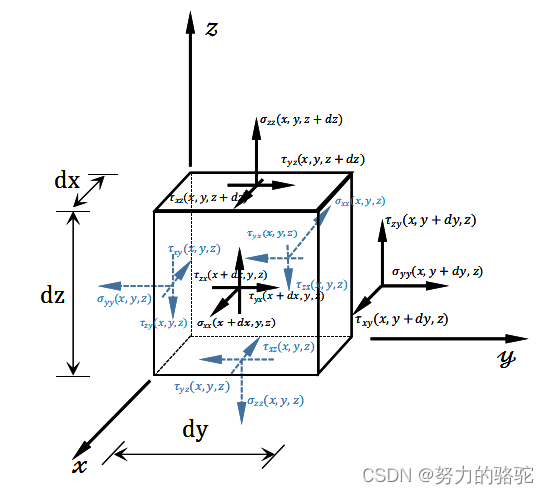
\quad\quad\quad\quad\quad\quad\quad\quad\quad 图1.1.1 微元体应力示意图
从牛顿第二定理（动量定理）可以列出微元体的平衡方程，如下所示：
$$\begin{gathered} {\sigma }_{xx}(x+dx,y,z)dydz-{\sigma }_{xx}(x,y,z)dydz+{\tau }_{xy}(x,y+dy,z)dxdz-{\tau }_{xy}(x,y,z)dxdz \\ +{\tau }_{xz}(x,y,z+dz)dxdy-{\tau }_{xz}(x,y,z)dxdy+b_{x}dxdydz=\rho \ddot{u}dxdydz\text{\hspace{1em}(1-1)} \end{gathered}$$
$$\begin{gathered} {\tau }_{yx}(x+dx,y,z)dydz-{\tau }_{yx}(x,y,z)dydz+{\sigma }_{yy}(x,y+dy,z)dxdz-{\sigma }_{yy}(x,y,z)dxdz \\ +{\tau }_{yz}(x,y,z+dz)dydz-{\tau }_{yz}(x,y,z)dydz+b_{y}dxdydz=\rho \ddot{v}dxdydz\text{\hspace{1em}(1-2)} \end{gathered}$$
$$\begin{gathered} {\tau }_{zx}(x+dx,y,z)dydz-{\tau }_{zx}(x,y,z)dydz+{\tau }_{zy}(x,y+dy,z)dxdz-{\tau }_{zy}(x,y,z)dxdz \\ +{\sigma }_{zz}(x,y,z+dz)dxdy-{\sigma }_{zz}(x,y,z)dxdy+b_{z}dxdydz=\rho \ddot{w}dxdydz\text{\hspace{1em}(1-3)} \end{gathered}$$
其中b为单位体积的体积力。选择上面第一个公式，将应力按一阶泰勒展开，则上式如下：

$$\begin{gathered} ({\sigma }_{xx}(x,y,z)+\frac{\partial {\sigma }_{xx}(x,y,z)}{\partial x}dx)dydz-{\sigma }_{xx}(x,y,z)dydz+ \\ ({\tau }_{xy}(x,y,z)+\frac{\partial {\tau }_{xy}(x,y,z)}{\partial y}dy)dxdz-{\tau }_{xy}(x,y,z)dxdz+ \\ ({\tau }_{xz}(x,y,z)+\frac{\partial {\tau }_{xz}(x,y,z)}{\partial z}dz)dxdy-{\tau }_{xz}(x,y,z)dxdy \\ +b_{x}dxdydz=\rho \ddot{u}dxdydz\text{\hspace{1em}(1-4)} \end{gathered}$$
经过整理，可以得到下式：
$$\frac{\partial {\sigma }_{xx}(x,y,z)}{\partial x}\cancel{dxdydz}+\frac{\partial {\tau }_{xy}(x,y,z)}{\partial y}\cancel{dxdydz}+\frac{\partial {\tau }_{xz}(x,y,z)}{\partial z}\cancel{dxdydz}+b_x\cancel{dxdydz}=\rho \ddot{u}\cancel{dxdydz}\text{\hspace{1em}(1-5)}$$
$$\frac{\partial {\sigma }_{xx}(x,y,z)}{\partial x}+\frac{\partial {\tau }_{xy}(x,y,z)}{\partial y}+\frac{\partial {\tau }_{xz}(x,y,z)}{\partial z}+b_x=\rho \ddot{u}\text{\hspace{1em}(1-6)}$$
其他两个方向的平衡方程同样的方法可得下式：
$$\frac{\partial {\tau }_{yx}(x,y,z)}{\partial x}+\frac{\partial {\sigma }_{yy}(x,y,z)}{\partial y}+\frac{\partial {\tau }_{yz}(x,y,z)}{\partial z}+b_y=\rho \ddot{v}\text{\hspace{1em}(1-7)}$$
$$\frac{\partial {\tau }_{zx}(x,y,z)}{\partial x}+\frac{\partial {\tau }_{zy}(x,y,z)}{\partial y}+\frac{\partial {\sigma }_{zz}(x,y,z)}{\partial z}+b_z=\rho \ddot{w}\text{\hspace{1em}(1-8)}$$
当研究的是静力学时，右边均等于零。

1.1.2.A 平衡方程的探讨

在建立微元体的平衡方程的过程中，我们实际上是假设应力等物理量是随着物质空间连续变化的，也就是说在平衡方程的构建中我们使用了连续性假设。
同时，我们在建立平衡方程的过程中，采用的是变形前的物体构形，实际上当物体在很大变形的过程中，采用变形前的物体构形来建立平衡方程是不准确的。例如，钓鱼竿钓鱼的过程就是大变形的过程，如果按照变形前的物体构形来列力平衡方程显然是不正确的，应该按照变形后的构形来列平衡方程。这也是非线性有限元与线性有限元的重要的区别点。

1.1.3 几何方程

观察微元体在受力前后的变形，见下图，其中黑色微元体为变形前，蓝色微元体为变形后，变形后微元体在三个坐标面上的投影见下图。

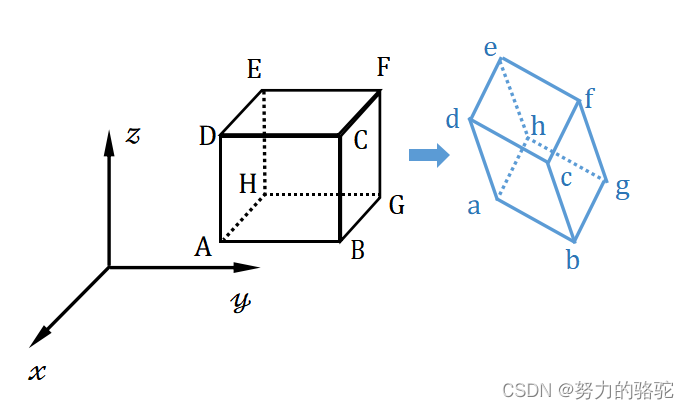
\quad\quad\quad\quad\quad\quad\quad\quad\quad 图1.1.2 微元体变形前后示意图

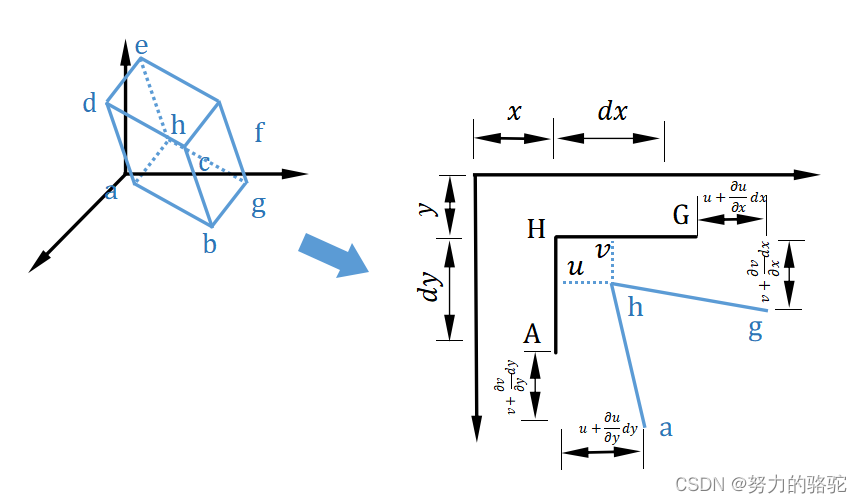
\quad\quad\quad\quad\quad\quad\quad\quad\quad 图1.1.3 变形前后微元体投影截面示意图

特别的以微元体变形前后在XOY面上的投影为例，定义x、y方向上的相对伸长量为
$${\epsilon }_{xx}=\frac{P^{{}^{\prime }}{A}^{{}^{\prime }}-PA}{PA}=\frac{\frac{\partial u}{\partial x}dx}{dx}=\frac{\partial u}{\partial x}\text{\hspace{1em}(1-9)}$$
$${\epsilon }_{yy}=\frac{P^{{}^{\prime }}{B}^{{}^{\prime }}-PB}{PB}=\frac{\frac{\partial v}{\partial y}dy}{dy}=\frac{\partial v}{\partial y}\text{\hspace{1em}(1-10)}$$
边线的夹角变化
$P^{{}^{\prime }}{A}^{{}^{\prime }}$与$PA$的夹角为
$$\alpha =\frac{(v+\frac{\partial v}{\partial x}dx)-v}{dx}=\frac{\partial v}{\partial x}\text{\hspace{1em}(1-11)}$$
$P^{{}^{\prime }}{B}^{{}^{\prime }}$与$PB$的夹角为
$$\beta =\frac{(u+\frac{\partial u}{\partial y}dy)-u}{dy}=\frac{\partial u}{\partial y}\text{\hspace{1em}(1-12)}$$
边线的夹角为两者的总和
$${\gamma }_{xy}=\alpha +\beta =\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\text{\hspace{1em}(1-13)}$$
综上，微元体变形前后在XOY面上的变形量(相对伸长量和夹角)与位移的关系式如下
$$\{\begin{array}{l}{\epsilon }_{xx}=\frac{\partial u}{\partial x}\\ {\epsilon }_{yy}=\frac{\partial v}{\partial y}\\ {\gamma }_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\end{array}\text{\hspace{1em}(1-14)}$$
微元体变形前后在YOZ面上的变形量(相对伸长量和夹角)与位移的关系式如下
$$\{\begin{array}{l}{\epsilon }_{yy}=\frac{\partial v}{\partial y}\\ {\epsilon }_{zz}=\frac{\partial w}{\partial z}\\ {\gamma }_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\end{array}\text{\hspace{1em}(1-15)}$$
微元体变形前后在XOZ面上的变形量(相对伸长量和夹角)与位移的关系式如下
$$\{\begin{array}{l}{\epsilon }_{xx}=\frac{\partial u}{\partial x}\\ {\epsilon }_{zz}=\frac{\partial w}{\partial z}\\ {\gamma }_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\end{array}\text{\hspace{1em}(1-16)}$$
综上所述，微元体的所有方向的变形量与位移的关系如下
$$\{\begin{array}{l}{\epsilon }_{xx}=\frac{\partial u}{\partial x}\\ {\epsilon }_{yy}=\frac{\partial v}{\partial y}\\ {\epsilon }_{zz}=\frac{\partial w}{\partial z}\\ {\gamma }_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\\ {\gamma }_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\\ {\gamma }_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\end{array}\text{\hspace{1em}(1-17)}$$
这种相对变形量我们称为应变。

1.1.3.A 几何方程的探讨

实际上，在几何方程中的线应变的度量是有条件的，我们观察下述案例

\quad\quad\quad\quad\quad\quad\quad\quad 图1.1.4 某微元体仅转动$\theta$示意图
假设P点坐标为(0,0)，A点坐标为(dx,0)，$A^{{}^{\prime }}$点坐标为
$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\cdot \left[\begin{array}{c}dx\\ 0\end{array}\right]\text{\hspace{1em}(1-18)}$$
那么由于转动了$\theta$角度后，引起的x方向的线应变为
$${\epsilon }_x=\frac{\delta }{dx}=\frac{\cos \theta dx-dx}{dx}=\cos \theta -1\approx 1-\frac{{\theta }^2}{2}+O({\theta }^4)-1\approx -\frac{{\theta }^2}{2}\text{\hspace{1em}(1-19)}$$
上述计算发现，就算变形体内的线段没有发生拉伸或者压缩，只要线段发生了转动，对应的线段各方向就存在线应变，这显然是不合适的，但是对于小变形和小转动情况下，我们的线应变度量采用如上公式事实上也是可行的。上式说明在小转动情况下转动角度引起的线应变的误差是转动角度的二次方量，如果感兴趣的应变量级是$10^{-2}$，那么1%的误差是能够接受的，这样的转动角度量级为$10^{-2}$，引起的应变误差按（1-19）式计算为$10^{-4}$量级。在大多数实际的结构分析中，一般的变形转动角度都非常小，基本能够满足应变精度。
但是我们主要要知道，线弹性力学中的线性应变度量实际上是默认在小变形和小转动情况下才能够成立的，这也是非线性有限元与线性有限元的主要区别点。

1.1.4 本构方程

材料的物理方程也叫本构方程是描述应力与应变（相对变形量）的关系。本文现在讨论的应力与应变的关系是限定在各向同性和线弹性的范畴内，这样的关系总体遵循广义胡克定律。
单向胡克定律，如下式：
$${\sigma }_x=E\cdot {\epsilon }_x\text{\hspace{1em}(1-20)}$$
再有泊松比的定义，可得Y和Z方向上的应力导致X方向的附加应变，遵循以下关系式：
$$\{\begin{array}{l}\mu =-\frac{{\epsilon }_x^y}{{\epsilon }_y}\\ \mu =-\frac{{\epsilon }_x^z}{{\epsilon }_z}\end{array}\text{\hspace{1em}(1-21)}$$
其中
$$\{\begin{array}{l}{\epsilon }_y=\frac{{\sigma }_y}{E}\\ {\epsilon }_z=\frac{{\sigma }_z}{E}\end{array}\text{\hspace{1em}(1-22)}$$
那么有
$${\epsilon }_x=\frac{{\sigma }_x}{E}-\mu (\frac{{\sigma }_y}{E}+\frac{{\sigma }_z}{E})\text{\hspace{1em}(1-23)}$$
同理，可得Y和Z方向的另外两个公式
$$\{\begin{array}{l}{\epsilon }_y=\frac{{\sigma }_y}{E}-\mu (\frac{{\sigma }_x}{E}+\frac{{\sigma }_z}{E})\\ {\epsilon }_z=\frac{{\sigma }_z}{E}-\mu (\frac{{\sigma }_x}{E}+\frac{{\sigma }_y}{E})\end{array}\text{\hspace{1em}(1-1)}$$
加上切应力和变形角度的关系，总共有六个方程
$$\{\begin{array}{l}{\epsilon }_x=\frac{{\sigma }_x}{E}-\mu (\frac{{\sigma }_y}{E}+\frac{{\sigma }_z}{E})\\ {\epsilon }_y=\frac{{\sigma }_y}{E}-\mu (\frac{{\sigma }_x}{E}+\frac{{\sigma }_z}{E})\\ {\epsilon }_z=\frac{{\sigma }_z}{E}-\mu (\frac{{\sigma }_x}{E}+\frac{{\sigma }_y}{E})\\ {\gamma }_{xy}=\frac{{\tau }_{xy}}{G}\\ {\gamma }_{yz}=\frac{{\tau }_{yz}}{G}\\ {\gamma }_{zx}=\frac{{\tau }_{zx}}{G}\end{array}\text{\hspace{1em}(1-24)}$$

1.1.4.A 本构方程的探讨

上述本构方程实际上是在线弹性及各项同性的情况下才能成立的，对于多数金属及多数结构设计中，基本能够满足各向同性和线弹性的假设，但是像橡胶、高分子材料等很多材料以及结构设计中金属进入塑性工作的都不满足线弹性的假设，像复合材料、单晶材料等不满足各项同性假设，所以这也是非线性有限元与线性有限元主要的区别点。

1.1.5 边界条件

实际物体必然存在力边界和位移边界的一种。位移边界顾名思义就是在这部分物质边界施加给定的位移，如下式
$$在边界S_u上有：\{\begin{array}{l}u=\hat{u}\\ v=\hat{v}\\ w=\hat{w}\end{array}\text{\hspace{1em}(1-25)}$$
力边界主要对应的力学本质是在物质表面附近的微元体也保持力平衡状态，具体来说，选取物质表面任意微元，如下图

微元三个方向的力平衡方程可以得到下述三式
$$\{\begin{array}{l}{\sigma }_{xx}\cdot \frac{1}{2}dydz+{\tau }_{zx}\cdot \frac{1}{2}dxdy+{\tau }_{yx}\cdot \frac{1}{2}dxdz=P_{x}dA\\ {\sigma }_{yy}\cdot \frac{1}{2}dxdz+{\tau }_{zy}\cdot \frac{1}{2}dxdy+{\tau }_{xy}\cdot \frac{1}{2}dydz=P_{y}dA\\ {\sigma }_{zz}\cdot \frac{1}{2}dxdy+{\tau }_{yz}\cdot \frac{1}{2}dxdz+{\tau }_{xz}\cdot \frac{1}{2}dydz=P_{z}dA\end{array}\text{\hspace{1em}(1-26)}$$
斜面面积和三个坐标面面积的关系为
$$\{\begin{array}{l}\frac{1}{2}dxdy=dA\cdot n_z\\ \frac{1}{2}dydz=dA\cdot n_x\\ \frac{1}{2}dxdz=dA\cdot n_y\end{array}\text{\hspace{1em}(1-27)}$$
代入上式，可得
$$在边界S_p上有：\{\begin{array}{l}{\sigma }_{xx}\cdot n_x+{\tau }_{zx}\cdot n_z+{\tau }_{yx}\cdot n_y=P_x\\ {\sigma }_{yy}\cdot n_y+{\tau }_{zy}\cdot n_z+{\tau }_{xy}\cdot n_x=P_y\\ {\sigma }_{zz}\cdot n_z+{\tau }_{yz}\cdot n_y+{\tau }_{xz}\cdot n_x=P_z\end{array}\text{\hspace{1em}(1-28)}$$

1.1.5.A 边界条件的探讨

在线弹性力学中的边界条件要么是位移边界要么是力边界，一般都是稳态线性的，符合叠加原理，这也是结构分析中大部分场景中实际存在的。但是像汽车碰撞、飞机鸟撞等这些实际发生的场景中，物体与物体发生接触和碰撞完全是动态的、部分随机的，物体间相互作用非线性的，这是非线性有限元与线性有限元主要的区别点。

1.1.6 线弹性力学的总结

这样就把弹性力学的所有求解方程和边界给列清楚了（当然弹性动力学的话要加上初值条件）。现在我们总结一下，弹性力学总共的方程和边界如下所示
$$\{\begin{array}{l}平衡方程：\{\begin{array}{l}\frac{\partial {\sigma }_{xx}(x,y,z)}{\partial x}+\frac{\partial {\tau }_{xy}(x,y,z)}{\partial y}+\frac{\partial {\tau }_{xz}(x,y,z)}{\partial z}+b_x=\rho \ddot{u}\\ \frac{\partial {\tau }_{yx}(x,y,z)}{\partial x}+\frac{\partial {\sigma }_{yy}(x,y,z)}{\partial y}+\frac{\partial {\tau }_{yz}(x,y,z)}{\partial z}+b_y=\rho \ddot{v}\\ \frac{\partial {\tau }_{zx}(x,y,z)}{\partial x}+\frac{\partial {\tau }_{zy}(x,y,z)}{\partial y}+\frac{\partial {\sigma }_{zz}(x,y,z)}{\partial z}+b_z=\rho \ddot{w}\end{array}\\ 几何方程：\{\begin{array}{l}{\epsilon }_{xx}=\frac{\partial u}{\partial x}\\ {\epsilon }_{yy}=\frac{\partial v}{\partial y}\\ {\epsilon }_{zz}=\frac{\partial w}{\partial z}\\ {\gamma }_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\\ {\gamma }_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\\ {\gamma }_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\end{array}\\ 本构方程：\{\begin{array}{l}{\epsilon }_x=\frac{{\sigma }_x}{E}-\mu (\frac{{\sigma }_y}{E}+\frac{{\sigma }_z}{E})\\ {\epsilon }_y=\frac{{\sigma }_y}{E}-\mu (\frac{{\sigma }_x}{E}+\frac{{\sigma }_z}{E})\\ {\epsilon }_z=\frac{{\sigma }_z}{E}-\mu (\frac{{\sigma }_x}{E}+\frac{{\sigma }_y}{E})\\ {\gamma }_{xy}=\frac{{\tau }_{xy}}{G}\\ {\gamma }_{yz}=\frac{{\tau }_{yz}}{G}\\ {\gamma }_{zx}=\frac{{\tau }_{zx}}{G}\end{array}\\ 边界条件：\{\begin{array}{l}{S}_u上有\{\begin{array}{l}u=\hat{u}\\ v=\hat{v}\\ w=\hat{w}\end{array}\\ S_p上有：\{\begin{array}{l}{\sigma }_{xx}\cdot n_x+{\tau }_{zx}\cdot n_z+{\tau }_{yx}\cdot n_y=P_x\\ {\sigma }_{yy}\cdot n_y+{\tau }_{xy}\cdot n_x+{\tau }_{zy}\cdot n_z=P_y\\ {\sigma }_{zz}\cdot n_z+{\tau }_{yz}\cdot n_y+{\tau }_{xz}\cdot n_x=P_z\end{array}\end{array}\end{array}\text{\hspace{1em}(1-29)}$$
总计15个方程、2类边界条件，待求量6个应力、6个应变、3个位移总共15个，必然存在一组解。当然有限元求解格式是不能直接应用这些方程的，需要找到一种等价方程的形式，这种形式就是最小能原理（虚功或者最小势能原理）。

1.1.6 非线性有限元与线性有限元的区别点

综上，非线性有限元与线性有限元主要的区别点就是以下三点：1.应力应变度量，以及匹配应力应变度量的平衡方程；2.本构方程；3.边界条件，我们分别成几何非线性、材料非线性和边界非线性。