- 光看概念可能很难,看代码就会很清晰,且简单。
- 动态规划算法要求马尔可夫决策过程是已知的,即要求与智能体交互的环境是完全已知的(例如迷宫或者给定规则的网格世界)。在此条件下,智能体其实并不需要和环境真正交互来采样数据,直接用动态规划算法就可以解出最优价值或策略。这就好比对于有监督学习任务,如果直接显式给出了数据的分布公式,那么也可以通过在期望层面上直接最小化模型的泛化误差来更新模型参数,并不需要采样任何数据点。
- 无模型的不需要事先知道环境的奖励函数和状态转移函数(其实这里的不知道是指通过反馈才能知道奖励和下一步转移到哪个state,是一个黑盒,而不像之前的动态规划,我们是知道一个表格 ,知道走哪一步是最好的,在这里只能真的去做了才能知道,才能得到反馈,这里的奖励是需要试探出来,他本身是有分布的,只是我们不知道他长什么样子。有点像扫雷),而是直接使用和环境交互的过程中采样到的数据来学习;
- 蒙特卡洛方法对价值函数的增量更新方式:

-
- 时序差分算法用当前获得的奖励加上下一个状态的价值估计来作为在当前状态会获得的回报

- sarsa算法,其实就是每次epsilon-greedy的方式选择下一个action,然后得到他的value,然后更新当前的action value。

- epsilon-greedy:有一定概率选择非最优的行为(action)。
- 为什么q-learniing是离线算法,因为:跳的时候(做下一个动作的时候)是epsilon-greedy选择下个一个action,更新action value的时候只选最优的下一个action value进行计算更新。那么就可以发现,更新不依赖于实时的action,所以这是离线算法。
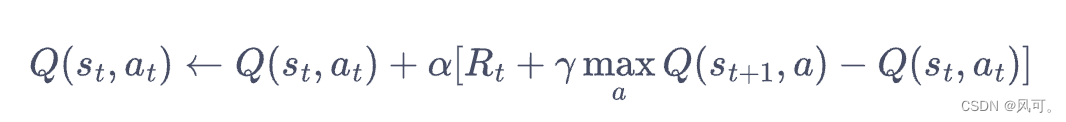
- sarsa和q-learning的区别:其实就一个,更新的时候sarsa是epsilon-greedy选择下一个action,得到他的value,q-learning是直接取最大的value。
sarsa
时序差分算法
class Sarsa:
""" Sarsa算法 """
def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
self.Q_table = np.zeros([nrow * ncol, n_action]) # 初始化Q(s,a)表格,记录action,那这个表就是策略表。
self.n_action = n_action # 动作个数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略中的参数
# def take_action(self, state): # 选取下一步的操作,具体实现为epsilon-贪婪
# if np.random.random() < self.epsilon:
# action = np.random.randint(self.n_action)
# else:
# action = np.argmax(self.Q_table[state])
# return action
def take_action(self, state, i): # 选取下一步的操作,具体实现为epsilon-贪婪
"""
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
刚开始大胆一点探索,后期小心一点,有点像学习率。
"""
## 设计一个epsilon随着步数增加减小。 采用了这种方式效果好了很多,
# if i< 10:
# self.epsilon = 1
# elif i<20:
# self.epsilon = 0.5
# elif i < 30:
# self.epsilon = 0.1
# elif i<40:
# self.epsilon = 0.05
# else:
# self.epsilon = 0.005
init_epsilon = 1
self.epsilon = init_epsilon * 0.9 ** (i/5) # 采用了这种方式效果好了很多
# print("epsilon: {}".format(self.epsilon))
if np.random.random() < self.epsilon:
action = np.random.randint(self.n_action)
else:
action = np.argmax(self.Q_table[state])
return action
def best_action(self, state): # 用于打印策略
Q_max = np.max(self.Q_table[state])
a = [0 for _ in range(self.n_action)]
for i in range(self.n_action): # 若两个动作的价值一样,都会记录下来
if self.Q_table[state, i] == Q_max:
a[i] = 1
return a
def update(self, s0, a0, r, s1, a1):
td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]
self.Q_table[s0, a0] += self.alpha * td_error
ncol = 12
nrow = 4
env = CliffWalkingEnv(ncol, nrow)
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
agent = Sarsa(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500 # 智能体在环境中运行的序列的数量
return_list = [] # 记录每一条序列的回报
for i in range(10): # 显示10个进度条
# tqdm的进度条功能
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)): # 每个进度条的序列数
episode_return = 0
state = env.reset()
action = agent.take_action(state, i*int(num_episodes / 10)+i_episode)
done = False
while not done:
next_state, reward, done = env.step(action) ## 环境
# next_action = agent.take_action(next_state) ## agent
next_action = agent.take_action(next_state, i*int(num_episodes / 10)+i_episode) ## agent
episode_return += reward # 这里回报的计算不进行折扣因子衰减,因为是从出发点到终止的return(不是每个state的return),作为评估loss。
agent.update(state, action, reward, next_state, next_action)
state = next_state
action = next_action
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Sarsa on {}'.format('Cliff Walking'))
plt.show()
# Iteration 0: 100%|██████████| 50/50 [00:00<00:00, 1206.19it/s, episode=50,
# return=-119.400]
# Iteration 1: 100%|██████████| 50/50 [00:00<00:00, 1379.84it/s, episode=100,
# return=-63.000]
# Iteration 2: 100%|██████████| 50/50 [00:00<00:00, 2225.14it/s, episode=150,
# return=-51.200]
# Iteration 3: 100%|██████████| 50/50 [00:00<00:00, 2786.80it/s, episode=200,
# return=-48.100]
# Iteration 4: 100%|██████████| 50/50 [00:00<00:00, 1705.21it/s, episode=250,
# return=-35.700]
# Iteration 5: 100%|██████████| 50/50 [00:00<00:00, 3393.12it/s, episode=300,
# return=-29.900]
# Iteration 6: 100%|██████████| 50/50 [00:00<00:00, 3694.32it/s, episode=350,
# return=-28.300]
# Iteration 7: 100%|██████████| 50/50 [00:00<00:00, 3705.87it/s, episode=400,
# return=-27.700]
# Iteration 8: 100%|██████████| 50/50 [00:00<00:00, 4115.61it/s, episode=450,
# return=-28.500]
# Iteration 9: 100%|██████████| 50/50 [00:00<00:00, 3423.20it/s, episode=500,
# return=-18.900]
q-learning
时序差分算法
class QLearning:
""" Q-learning算法
跳时候是epsilon-greedy选择下个一个action,更新的时候只选最优的action value进行更新。那么就可以发现,更新不依赖于实时的action,所以这是离线算法。
"""
def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
self.Q_table = np.zeros([nrow * ncol, n_action]) # 初始化Q(s,a)表格
self.n_action = n_action # 动作个数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略中的参数
def take_action(self, state): #选取下一步的操作
if np.random.random() < self.epsilon:
action = np.random.randint(self.n_action)
else:
action = np.argmax(self.Q_table[state])
return action
def best_action(self, state): # 用于打印策略
Q_max = np.max(self.Q_table[state])
a = [0 for _ in range(self.n_action)]
for i in range(self.n_action):
if self.Q_table[state, i] == Q_max:
a[i] = 1
return a
def update(self, s0, a0, r, s1):
td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]
self.Q_table[s0, a0] += self.alpha * td_error
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
agent = QLearning(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500 # 智能体在环境中运行的序列的数量
return_list = [] # 记录每一条序列的回报
for i in range(10): # 显示10个进度条
# tqdm的进度条功能
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)): # 每个进度条的序列数
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done = env.step(action)
episode_return += reward # 这里回报的计算不进行折扣因子衰减
agent.update(state, action, reward, next_state)
state = next_state
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Q-learning on {}'.format('Cliff Walking'))
plt.show()
action_meaning = ['^', 'v', '<', '>']
print('Q-learning算法最终收敛得到的策略为:')
print_agent(agent, env, action_meaning, list(range(37, 47)), [47])
# Iteration 0: 100%|██████████| 50/50 [00:00<00:00, 1183.69it/s, episode=50,
# return=-105.700]
# Iteration 1: 100%|██████████| 50/50 [00:00<00:00, 1358.13it/s, episode=100,
# return=-70.900]
# Iteration 2: 100%|██████████| 50/50 [00:00<00:00, 1433.72it/s, episode=150,
# return=-56.500]
# Iteration 3: 100%|██████████| 50/50 [00:00<00:00, 2607.78it/s, episode=200,
# return=-46.500]
# Iteration 4: 100%|██████████| 50/50 [00:00<00:00, 3007.19it/s, episode=250,
# return=-40.800]
# Iteration 5: 100%|██████████| 50/50 [00:00<00:00, 2005.77it/s, episode=300,
# return=-20.400]
# Iteration 6: 100%|██████████| 50/50 [00:00<00:00, 2072.14it/s, episode=350,
# return=-45.700]
# Iteration 7: 100%|██████████| 50/50 [00:00<00:00, 4244.04it/s, episode=400,
# return=-32.800]
# Iteration 8: 100%|██████████| 50/50 [00:00<00:00, 4670.82it/s, episode=450,
# return=-22.700]
# Iteration 9: 100%|██████████| 50/50 [00:00<00:00, 4705.19it/s, episode=500,
# return=-61.700]
# Q-learning算法最终收敛得到的策略为:
# ^ooo ovoo ovoo ^ooo ^ooo ovoo ooo> ^ooo ^ooo ooo> ooo> ovoo
# ooo> ooo> ooo> ooo> ooo> ooo> ^ooo ooo> ooo> ooo> ooo> ovoo
# ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
# ^ooo **** **** **** **** **** **** **** **** **** **** EEEE



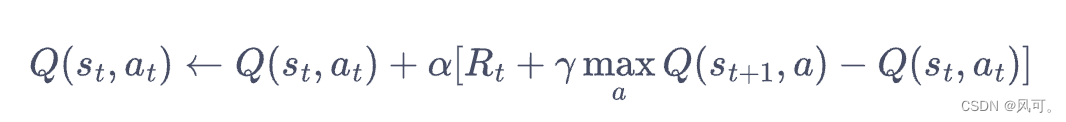








 博客围绕强化学习中的Sarsa和Q-learning算法展开。介绍了动态规划算法和无模型算法的特点,阐述了蒙特卡洛方法和时序差分算法。详细说明了Sarsa和Q-learning算法的更新方式,指出二者区别在于更新时Sarsa用epsilon-greedy选下一个动作值,Q-learning取最大值。
博客围绕强化学习中的Sarsa和Q-learning算法展开。介绍了动态规划算法和无模型算法的特点,阐述了蒙特卡洛方法和时序差分算法。详细说明了Sarsa和Q-learning算法的更新方式,指出二者区别在于更新时Sarsa用epsilon-greedy选下一个动作值,Q-learning取最大值。
















 1436
1436

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








