哈希冲突的概率

哈希冲突的概率

一个Hash函数由指定类型的项和一个在指定范围内生成的Hash值组成。输入的每一项可能是任何事物：字符串，文件，甚至目录。相同的输入总能生成相同的Hash值，并且一个好的Hash函数总是致力于不同的Hash输入得到不同的值。

一个Hash函数并不知道在输入集合中的其他项，当一个输入项通过它时，它仅仅进行着一些按位与/或操作，因此，总有2个不同的输入项，得到相同Hash值的可能。
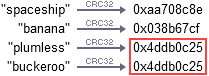
举个众所周知的Hash函数CRC32，如果你给这个Hash函数“plumless” 和“buckeroo”这2个字符串，它会生成相同的Hash值，这是已知的Hash冲突。

计算Hash冲突的概率

虽然已经很多可以选择的Hash函数，但创建一个好的Hash函数仍然是一个活跃的研究领域。一些Hash函数是快的，一些是慢的，一些Hash值均匀地分布在值域上，一些不是。如果你对一些。对于我们的目的，让我们假设这个Hash函数是非常好的。它的Hash值均匀地分布在值域上。

在这种情况下，对于一个输入集合生成的Hash值是非常像生成一个随机数集合。我们的问题转化为如下：
        给K个随机值，非负而且小于N,他们中至少有个相等的概率是多少？
实际上我们求这个问题的对立问题更加简单：他们都不相同的概率是多少？无论这个对立问题的结果是多少，我们用1减去对立问题的结果就得到原问题的结果。

对于一个值域为N的Hash值，假设你已经挑选出一个值。之后，剩下N-1个值是不同于第一个值的，因此，对于第二次随机生成不同第一个数的概率为N/N-1.
简而言之，有N个不同的数，你第一次挑选出某个，然后继续从N个数中挑选，那只要不是选到和第一次一样的那个数一样就不一样喽，所以概率为N-1/N。
之后就是第三次挑选，第三次挑选出的第三个数要求不同于前两个数，所以概率就为N-1/N*N-2/N.
一般的，随机生成K个数，他们都不相同的概率为：

计算机中，对于K很大的时候计算很麻烦，幸运的是，上面的表达式近似于

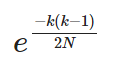
这个会更快得计算，我们如何知道这是一个好的近似。我们看一下分析过程，使用泰勒公式和epsilon-delta proof，这个误差趋于0当N增大的时候。或者，更简单，你可以计算2者的值然后比较他们，运行下面的python代码，你会感觉到这个近似是多么准确：

import math
N = 1000000
probUnique = 1.0
for k in xrange(1, 2000):
    probUnique = probUnique * (N - (k - 1)) / N
    print k, 1 - probUnique, 1 - math.exp(-0.5 * k * (k - 1) / N)

好的，这个奇妙的表达式作为我们每个值都不一样的结果，然后我们用1减去得到Hash冲突的概率

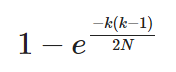
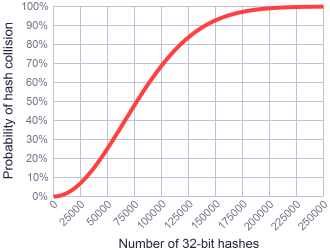
这是一个 N=2^32的图，它说明了使用32bit的Hash值的冲突概率，当Hash数是77163时，发生碰撞的可能为50%,这是有价值的。而且注意无论N区任意值都会得到一个类似S曲线的图。

简化表达式

这是非常有趣的，我们的表达式是1-e^-x这种形式，下面近似这仅仅在X较小的时候误差非常小，1/10或更小：

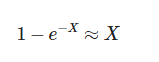
换句话说，这个表达式非常好的近似于它自己的指数，实际上x越小，越准确，所以小的冲突概率，我们能使用这个简化表达式

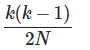
这实际上是一个非常方便的表示。因为它避免了一些在原表达式中的精度问题。浮点型数字在非常接近1的时候表示不是很好。

此外，如果N远大于K,K和K-1并没有什么大区别。所以我们可以更加化简为：K^2/2N

一些冲突概率

在某些应用中，例如将Hash值作为ID,避免冲突是非常重要的。这是非常好的概率是更小的原因。

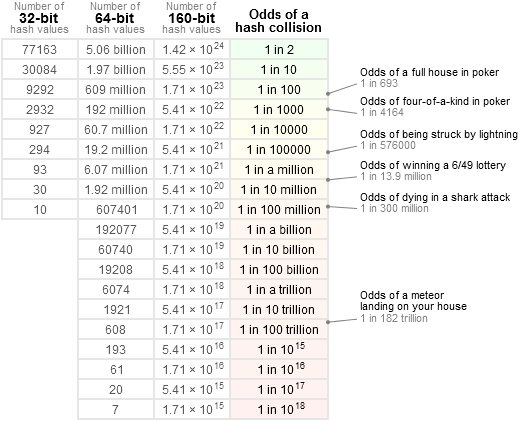
假设Hash值是32位，64位，160位，下表包括了小概率的范围。如果你知道Hash值的取值数量，非常简单地找到这个最近的行，我们以挂彩排中奖的角度去看这个冲突概率