惠更斯原理

本文链接：https://blog.csdn.net/u013669912/article/details/142623284

注：本文为 “惠更斯原理 | 驻波模型” 相关文章合辑。

图片清晰度限于原文原状，如有内容异常，请看原文。

未整理去重。

怎样优雅地画驻波模型图和惠更斯原理图？

原创薛德堡物含妙理 2024年09月28日 17:42 广东

在讲本文主题之前，诸君先思考一个稍微简单点的问题：若将函数图像的横轴弯曲，例如变成圆，则函数图像将如何变化？

例如，函数 $\displaystyle {y}=\sin (3x)$ 的图像：

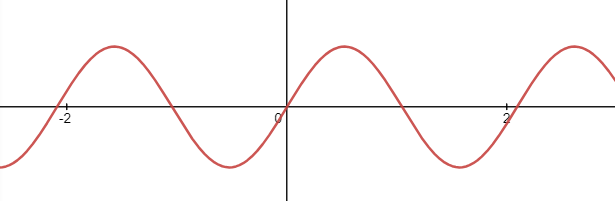
若把它的横轴替换成半径为 10 的圆，则是下面这个样子。

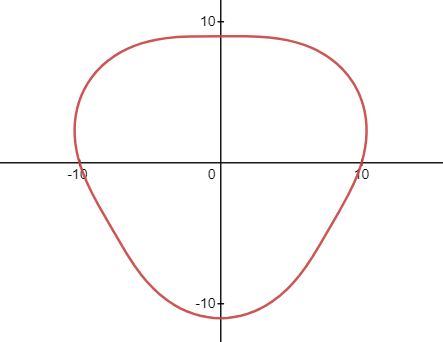
是不是很无聊？为什么要做这种无用的事？

不不不，这件事在物理学中很重要。

1913 年，丹麦物理学家玻尔（Niels Bohr，1885-1962）在卢瑟福模型和巴耳末公式的启发下，提出了一种新的氢原子结构模型。

Niels Bohr (1885-1962) 尼尔斯·玻尔

该模型后被称作 “波尔模型”，它包含三条假设，即定态假设，频率假设和量子化假设。玻尔模型几乎与所有的实验结果一致，波尔大获成功。

量子化条件即 $L=n\hbar$ ，其中 $L$ 为角动量， $n$ 为从 1 开始的整数， $\hbar=h/(2\pi )$ ，考虑圆轨道运动，则

$L=|r\times p|=rmv$

故得 $rmv=nh/(2\pi )$ ，即

$\displaystyle\frac{2\pi \text{r}}{n}=\frac{h}{mv}$

1924 年，法国物理学家德布罗意（Louis de Broglie，1892-1987）提出的物质波假设，即

$\displaystyle\lambda =\frac{h}{p}$ , $\nu =\frac{E}{h}$

其中 $\displaystyle lambda$ 是电子的波长，不考虑相对论时 $p=m\nu$ ，故得

$\displaystyle 2\pi r=n\lambda$

所以，氢原子的电子轨道的周长是其波长的整数倍，这就是氢原子的驻波模型。

若要把驻波模型的样子给画出来，该怎么画呢？

没错！就按照上述思路，将正弦函数移植到圆上就行了。

假设圆轨道周长是波长的 9 倍，波的几率幅为 1，则在半径为 10 的圆上画出来是这样的：

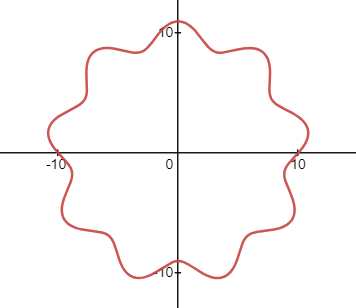
那么，具体是怎么个移植法呢？

很简单，只要在圆的半径上叠加函数值 $y$ ，作为径向距离就行了。

例如上面这个，叠加后在直角坐标系中的径向距离是

$\displaystyle\sqrt{{{x}^{2}}+{{y}^{2}}}=10+\sin (9\arctan (\frac{y}{x}))$

其中 $a rc t an$ 是为了得到 $\theta$ 。不过，因为 $a rc t an$ 的定义域的问题，画出来的图有断点。

换成极坐标就可以完美解决问题，径向距离用 $r$ 表示，即

$\displaystyle r=10+\sin (9\theta )$

在网上找一个绘图程序，直接输入上式，就得到上面的图形了。

在此推荐一个很好用的绘图工具 $G r a p h Pl o tt er$ ，地址为：

Graph Plotter
https://www.transum.org/Maths/Activity/Graph/Desmos.asp

如果将圆轨道以虚线画出来，加上驻波曲线，得到 $n = 9$ 时的驻波模型图如下。

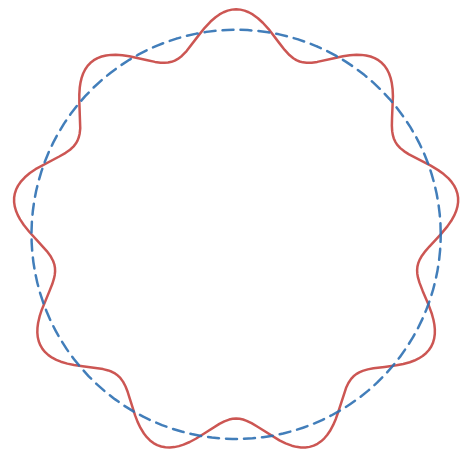
下面到本文的第二个问题 —— 画惠更斯原理图。

Christiaan Huygens (1629-1695)

1678 年，荷兰物理学家惠更斯 (Christiaan Huygens，1629-1695) 为了解释波的传播，提出：

介质中波动传播到的各点都可以看作是发射子波的子波源，而在其后的任意时刻，这些子波的包络面就是新的波前。

此即惠更斯原理。据此原理，平面波在均匀介质中保持为平面波，而球面波也保持为球面波，如下图所示。

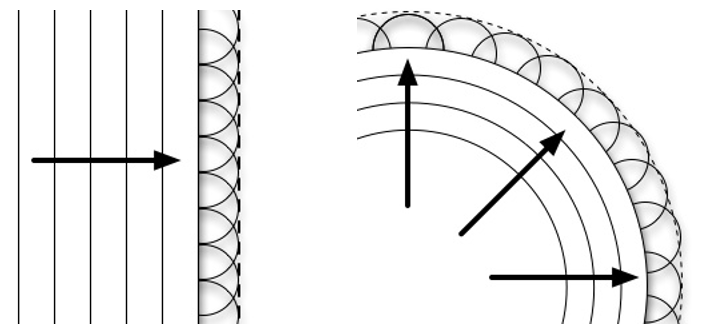
怎样优雅地画出上面这样的图呢？

当然，你可以用任何高级语言编个程序来完成，但总感觉那样太大动干戈了。能否像上面画驻波模型那样简单呢？

当然可以！只要先把半圆排成一列，再像上面那样，移植到一个大圆上就行了。

但问题来了，半圆的方程为

$\displaystyle {y=}\sqrt{100-{{x}^{2}}}$

其图像如下：

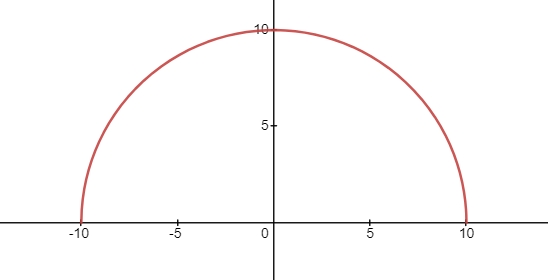
它不是周期函数啊！怎么才能排成一列呢？

有人可能会说，很简单啊，只要这样就行了：

$\sqrt{100-(x - 20n)^{2}},n = 0,\pm1,\pm2,\cdots$

$x\in[20n - 10,20n + 10)$ ，但由于借助了整数 $n$ ，这个周期函数无法被网上的函数绘图程序识别。

怎样才能借助通用的算符构造一个周期函数呢？

读到这里，在看本人给出的方法之前，诸君可先独立思考一下，说不定你可以有更简单的方法。

本人原创的方法很简单，借助神奇的算符 $m o d$ ，它是用来取余的，例如：

$m o d (11, 10) = 1$

由于它是一个通用的函数符号，就像 $s in$ 和 $cos$ 那样，几乎所有的程序都认识它，所以可以放心使用。

借助它，基于半圆，构造周期函数为：

$y=\sqrt{100-(10 - mod(x,20))^{2}}$

画出来是下面这样的

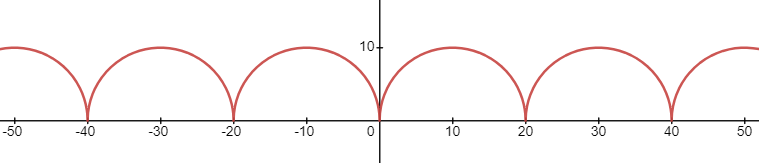
若想往左移动一个半径的距离，可改为如下形式：

$y=\sqrt{100-(10-\vert10 - mod(x,20)\vert)^{2}}$

这样画出来就是

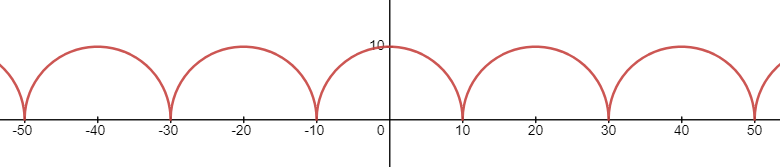
我想诸君应该看出规律了吧！

是的！任何函数，只要用 $m o d$ 函数，把自变量 $x$ 变成

$\displaystyle\frac{T}{2}-\bmod (x,T)$

就得到一个周期为 $T$ 的函数了！

例如函数 $\displaystyle y = \vert x\vert$ ，它的图像为

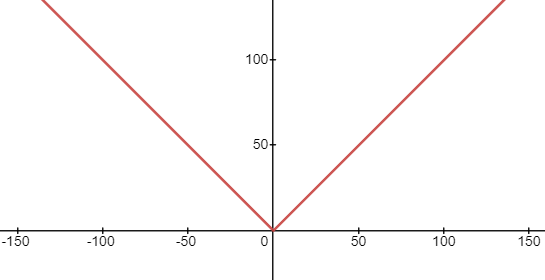
按上述规则，得到周期为 20 的函数为

$\displaystyle y=\vert10 - mod(x,20)\vert$

其图像为

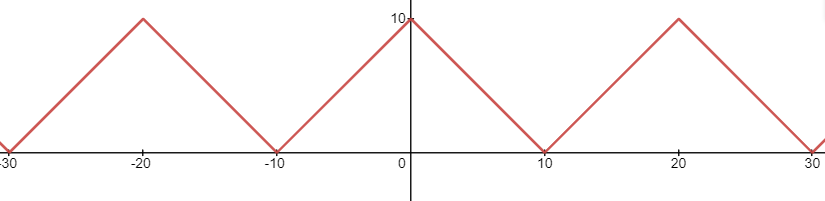
再例如，对抛物线 $y = x^{2}$ ，对应周期为 20 的函数为

$\displaystyle y=(10 - mod(x,20))^{2}$

其图像为

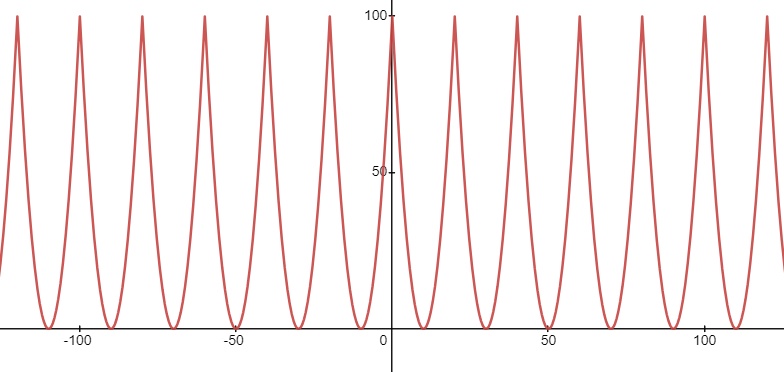
好了，构造周期函数的的问题解决了，现在可以画惠更斯原理图了！

根据上面所讲，有了基于半圆构造的周期函数，只需将它移植到一个波阵面上就行了。

例如半径为 $10\pi$ 的半圆，构造周期为 $20\pi$ 函数为

$\displaystyle y=\sqrt{100\pi^{2}-(10\pi - mod(x,20\pi))^{2}}$

将它移植到半径为 100 的球面波上，显然，此时自变量相当于大圆上走过的路径长，即

$\displaystyle x = 100\theta$ ，

故得绘图函数为

$\displaystyle r = 100+\sqrt{100\pi^{2}-(10\pi - mod(100\theta,20\pi))^{2}}$

画出的图为

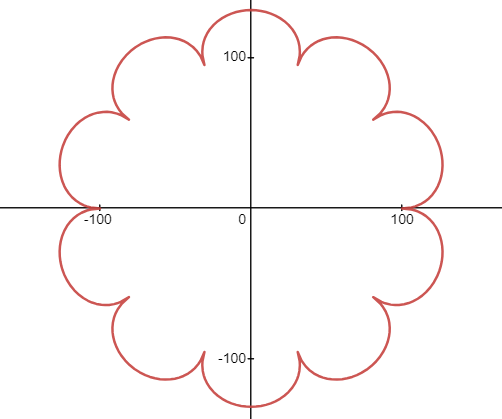
若同时画上内外两个大圆，则得到球面波的惠更斯原理图如下。

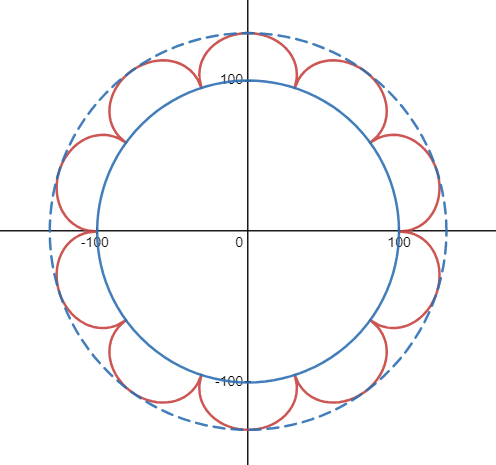
至于平面波，基于半圆的周期函数图就是惠更斯原理图，不再赘述。

作为全文总结，把两个驻波和一组球面波组合，得到一朵奇妙的花 —— 源自物理世界的理性之花。

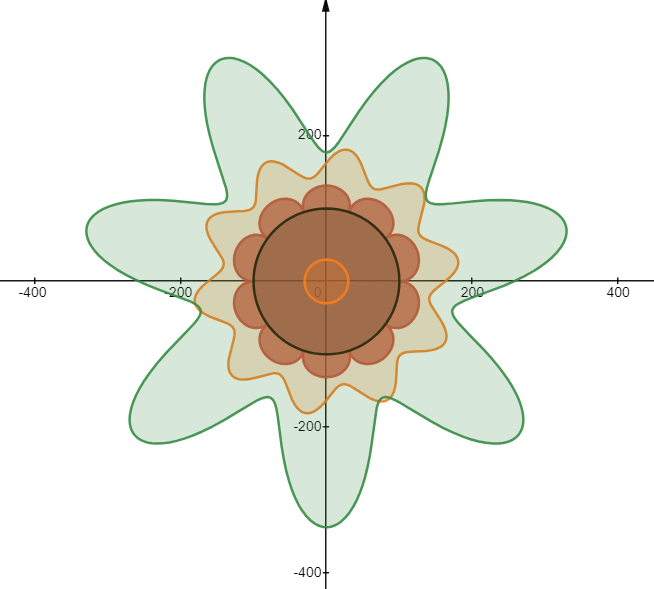
凡是看到这朵美丽之花的人，都会有好运。

关于惠更斯原理图画法的一点补充

在上文中，通过基于 $m o d$ 函数构造的周期函数，给出了一种绘制惠更斯原理图的简单方法。

原文发布后，自我感觉有两个地方不够完美，故作补充说明。

第一，构造周期函数后，自变量任意偏移后的图像画法，原文没有给出。

例如半圆函数，其周期函数为：

$\text{y}=f(x)=\sqrt{100-(10-\bmod {{(x,20)}^{2}})}$

若要向右偏移 $\Delta \text{x}$ ，只需要在 $x$ 后减 $\Delta \text{x}$ 即可，即

$\text{y}'=f(x-\Delta x)$

例如下面是周期函数（红色线），以及分别偏移 5，10 和 15 后的 3 个函数，画在一起的效果图。

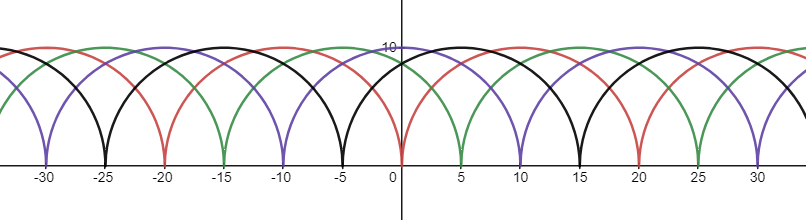
第二，原文中，惠更斯原理图没有采用流行的画法。

具体讲就是小球面波相互交错。相邻小圆不是相切，而是过彼此的圆心，如下图所示。

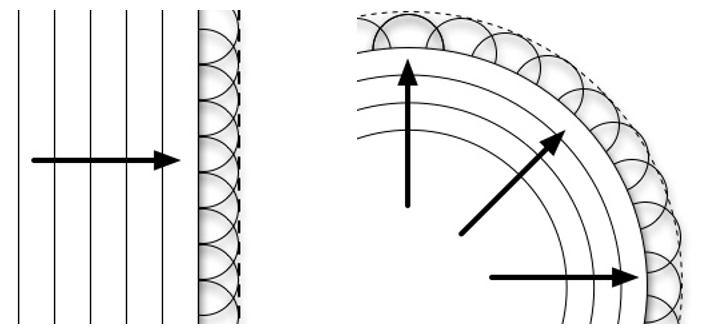
其实这一点很容易做到，只要再加一个偏移半个周期的图像即可。

例如，对原文中半径为 $10\pi$ 的半圆，构造周期为 $20\pi$ 函数为

$\text{y}=f(x)=\sqrt{100{{\pi }^{2}}-{{(10\pi -\bmod (\pi ,20\pi ))}^{2}}}$

它偏移半个周期的函数为

${{\text{y}}^{'}}=f(x-10\pi )$

它们分别移植到半径为100的球面上后，得到的绘图函数分别为

$\text{r}=100+f(100\theta )$

和

$\text{r}'=100+f(100\theta -10\pi )$

两个图画在一起，效果如下

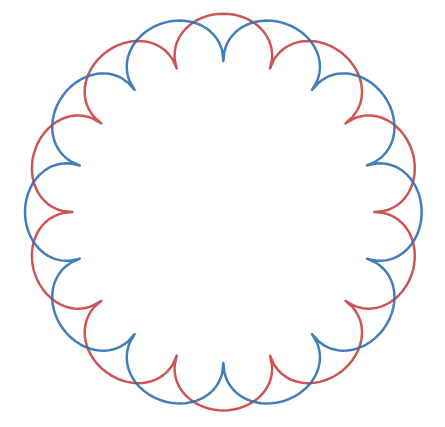
加上内外两个大圆，就是流行的惠更斯原理图的画法，即

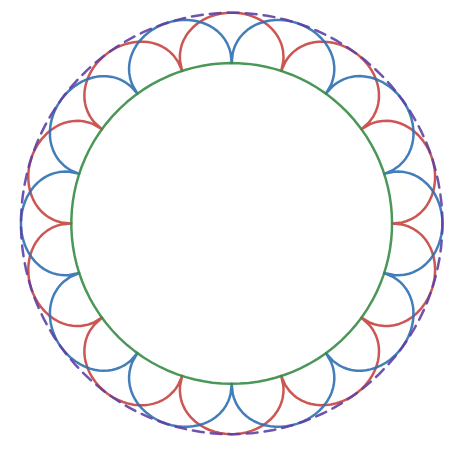
但需要指出的是：这种画法并不是必须的！

有人认为这样画法才能保证包络线是圆，这种理解是不对的！

因为，无论交错的圆多么密集，只要不是无限密，它们的包络线就不可能是完美圆形！

例如，上面的周期函数 $f(x)+f(x-10\pi )$ 的图像，得到的图形如下

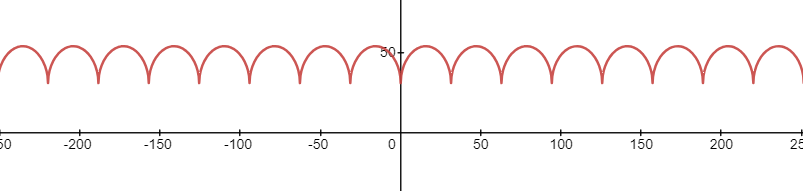
图像并非水平直线！这说明

$r+r'\ne const$

所以，惠更斯原理图的流行画法中，小圆的包络线不是圆形！

既然如此，交错圆的画法并无必要。

因此，原文中中对惠更斯原理图的如下画法，虽不流行，但并无不妥。

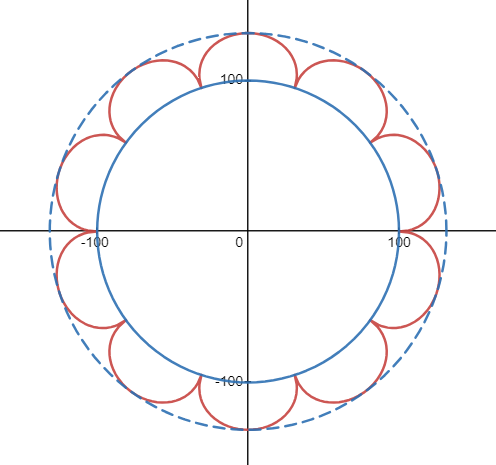
再顺便看看，有没有周期函数，它移植到圆上后，能通过有限的偏移函数相加后得到完美圆形？

第一个例子，方波周期函数，即

$\displaystyle f(x)=\frac{\sin (x)}{\sqrt{{{\sin }^{2}}(x)}}$

它的图像为

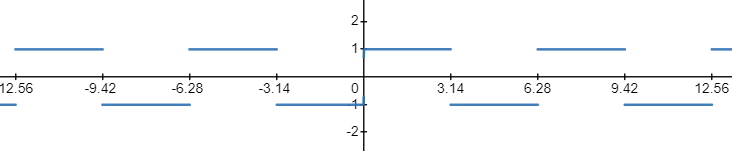
显然

$\displaystyle f(x)+f(x-\pi )=0$

所以，此函数移植到圆上之后，与偏移半个周期的函数叠加后，图像是圆形。

第二个例子，函数 ${{\sin }^{2}}(x)$ 和 ${{\cos}^{2}}(x)$ ，由于满足

${{\sin }^{2}}(x)+{{\sin }^{2}}(x-\frac{\pi }{2})=1$

和

${{\cos }^{2}}(x)+{{\cos }^{2}}(x-\frac{\pi }{2})=1$

当移植到圆上后，它们分别与偏移半个周期的函数叠加后的图像，也是圆形。

除此之外，还有没有什么周期函数，能通过与有限的偏移函数相加得到常数？

留给读者思考。

END

自然现象中常见的驻波

东软物理社团 2022 年 04 月 15 日 10:42

什么是波啊？

What is wave？

驻波是指频率相同、传输方向相反的两种波（不一定是电波），沿传输线形成的一种分布状态。其中的一个波一般是另一个波的反射波。在两者电压（或电流）相加的点出现波腹，在两者电压（或电流）相减的点形成波节。在波形上，波节和波腹的位置始终是不变的，给人 “驻立不动” 的印象，但它的瞬时值是随时间而改变的。如果这两种波的幅值相等，则波节的幅值为零。

来看两种生活中熟悉的小现象

水波纹和音叉

声音由音源的振动产生，我们都曾在高中课堂见到过音叉。敲打音叉后，音叉的尖齿来回振动，扰动周围的空气分子。这些扰动通过粒子相互作用传递到相邻的空气分子上，这样音叉产生的声音就可以通过空气（介质）传播了。

当然，有一种波比较特殊，那就是电磁波。电磁波一般是由电荷变速产生变化的电场，变化的电场产生磁场，进而变化的磁场产生电场。感应电场与磁场之间的这种相互作用会在空间上导致电磁波的传播。

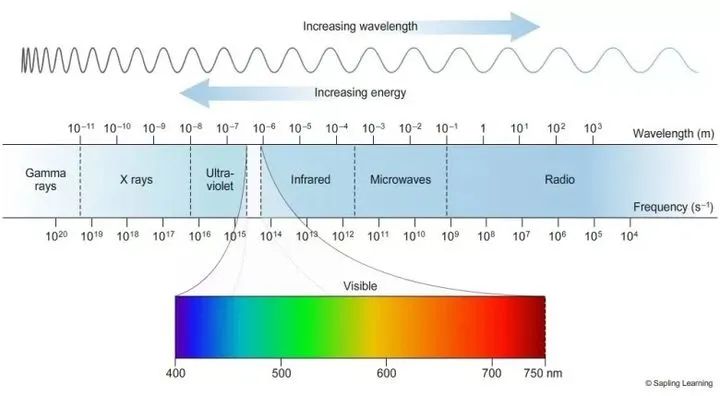
电磁波频谱图

电磁波剖面图

驻波的形成：

两列沿相反方向传播的振幅相同、频率相同的波叠加时形成的波叫做驻波。那么，怎样得到两列沿相反方向传播的波，而且这两列波的振幅和频率都相同呢？在实践中一般是利用了波的反射。比如说弦上的驻波，当声波传播到固定端时会发生反射，反射波与入射波传播方向相反，振幅和频率都相同。因此，入射波和反射波的叠加形成驻波。对于管中的驻波，当声波传播到闭口端时同样发生反射，入射波和反射波叠加形成驻波。由于弦的固定端和管的闭口端相当于波在传输过程中遇到的障碍物，因此对于波在弦的固定端和管的闭口端发生反射是比较容易接受的。然而，对于管中的驻波，还有另外一种情况是两端开口的管中形成的驻波。这样一来，驻波的形成原理解释为波源在一个开口端发生振动产生入射波。入射波传播到另一个开口端时发生反射，入射波和反射波叠加形成驻波。

说到这里，可能你们会比较疑惑，这跟我们的日常生活有什么联系呢？

其实联系是很大的，最简单的就是无线充电！

无线充电技术，源于无线电能传输技术，可分为小功率无线充电和大功率无线充电两种方式。

小功率无线充电常采用电磁感应式，如对手机充电的 Qi 方式。大功率无线充电常采用谐振式，由供电设备将能量传送至用电的装置，该装置使用接收到的能量对电池充电，并同时供其本身运作之用。

由于充电器与用电装置之间以磁场传送能量，两者之间不用电线连接，因此充电器及用电的装置都可以做到无导电接点外露。

无线充电

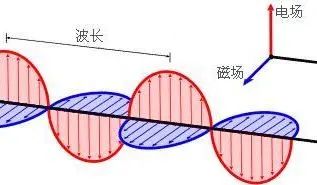
电磁波

还有其他类型的波。比如：在引力场中根据广义相对论传播扰动的引力波、结合了机械变形和电磁场效应的等离子波、热扩散波和反应扩散波等等。生活中常见的波有很多很多。当然，情绪波动可不是我们要学的波哦！我们也不学动感光波哦！

热扩散波

波的特性是什么呢

可以叠加也可以互相干扰

一般会将波的振动方向与传播方向之间的关系将波分为横波与纵波。

入射波与反射波相互干扰而形成的波形不再推进的波浪，称驻波。驻波多发生在海岸陡壁或直立式水工建筑物前面。紧靠陡壁附近的海水面随时间虽作周期性升降，海水呈往复流动，但并不向前传播，水面基本上是水平的，这就是由于受岸壁的限制使入射波与反射波相互干扰而形成的。波面随时间作周期性的升降，每隔整数个半个波长就有一个波面升降幅度为最大的断面，称为波腹；当波面升降的幅度为 0 时的断面，称为波节。相邻两波节间的水平距离仍为半个波长，因此驻波的波面包含一系列的波腹和波节，腹节相间，波腹处的波面的高低虽有周期性变化，但此断面的水平位置是固定的，波节的位置也是固定的。这与进行波的波峰、波谷沿水平方向移动的现象正好相反，驻波的形状不传播，故名驻波。当波面处于最高和最低位置时，质点的水平速度为零，波面的升降速度也为零；当波面处于水平位置时，流速的绝对值最大，波面的升降也最快，这是驻波运动独有的特性。

特点：两个波的频率、传播速度完全相等，但方向相反。

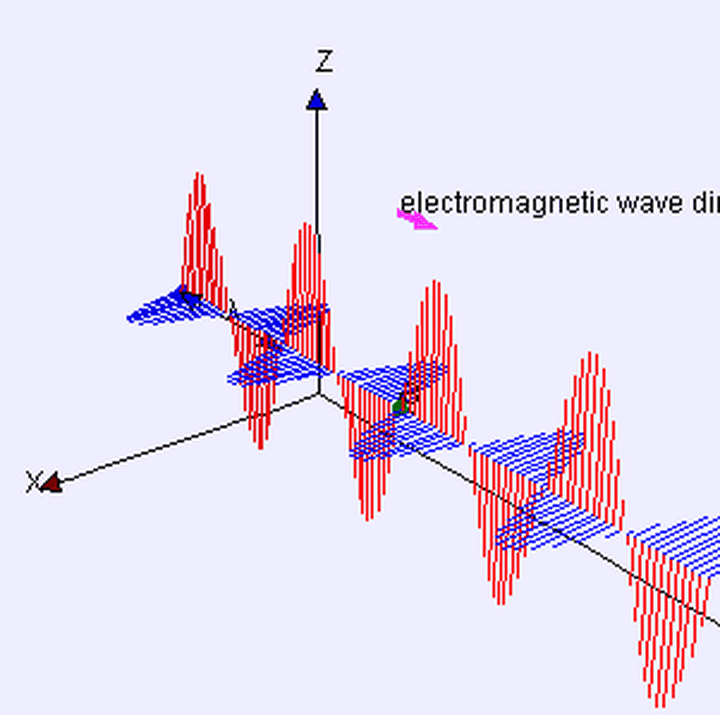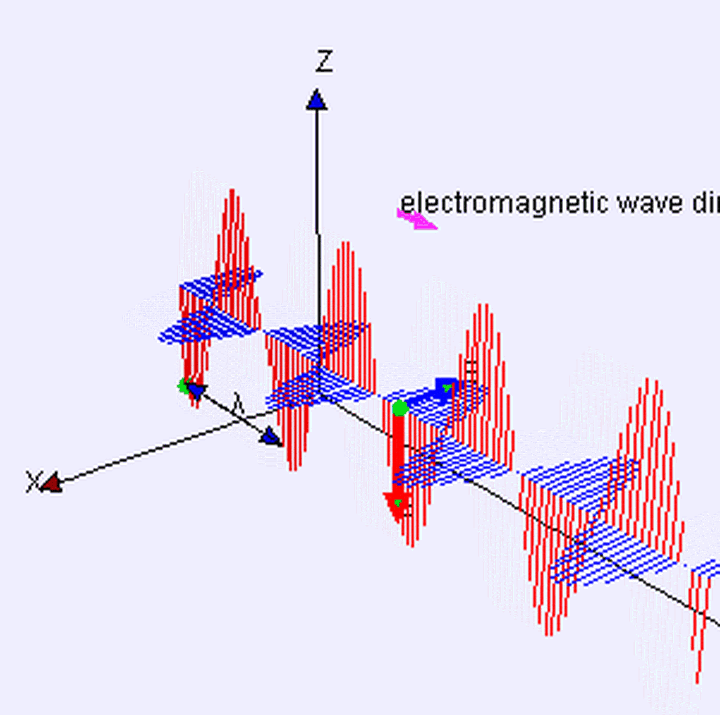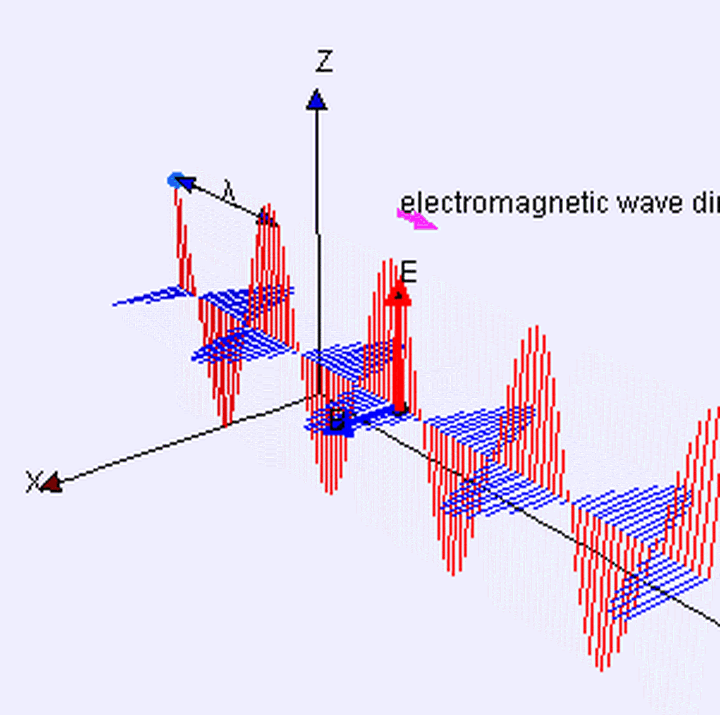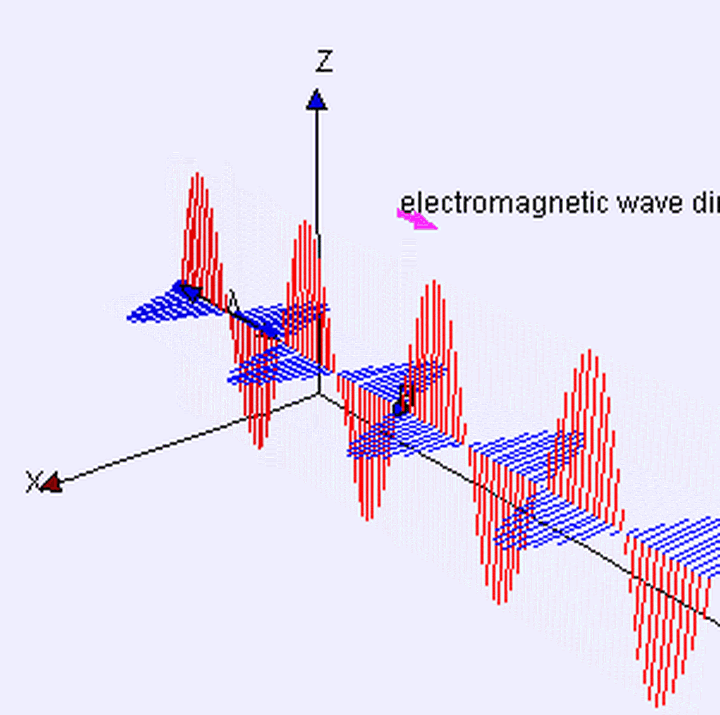
经典电磁波模型

叠加波

横波也称 “凹凸波”，是质点的振动方向与波的传播方向垂直。横波的特点是质点的振动方向与波的传播方向相互垂直。在横波中突起的部分为波峰，凹下部分叫波谷。波长通常是指相邻两个波峰或波谷之间的距离。

电磁波、光波都是横波。

纵波是质点的振动方向与传播方向平行的波。在纵波中波长是指相邻两个密部或疏部之间的距离。

如敲锣时，锣的振动方向与波的传播方向就是平行的，声波是纵波。一个可以穿过整个地球的主要的（压缩的）地震波，命名原因是它是在地震期间到达地震仪驻地的第一波。

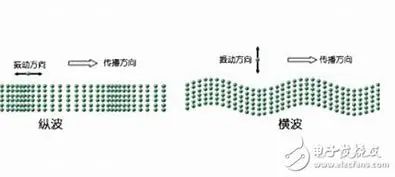
纵波与横波

声波发生器

行波（travelling wave）是指平面波在传输线上的一种传输状态，其幅度沿传播方向按指数规律变化，相位沿传输线按线性规律变化。从相邻时刻进行考察，可以发现波形随时间的增长而向传输线的终端移动。

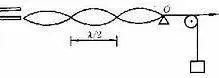
行波

牛顿第三定律告诉我们，力的作用是相互的，且两个物体之间的作用力与反作用力大小相等，方向相反，作用在同一直线上。

而应用牛三的原理，也可以形成我们所说的驻波，而且是非常美丽的驻波。

马赫环简介

马赫环又称马赫盘，是当气流以超音速和低于外部大气的压强离开喷嘴时发生的一种气体现象，呈现等间距圆环的形状，常见于火箭发动机或喷气发动机的排气羽流中。

原理：当气体过膨胀时，与外部大气相比，排气中的气体压强较低，导致排气被压缩或向内挤压。这种压缩会增加排气压强。然而，由于流量可能被压缩得太多，以致其压强超过大气压强。此时，气流再次向外扩张以降低压强。

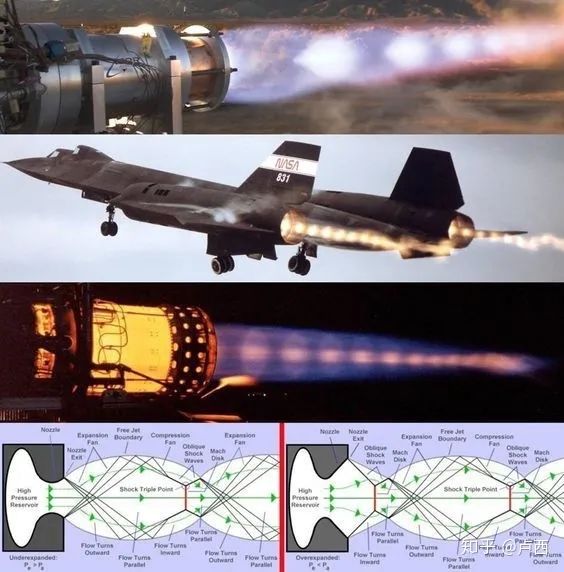
各种结构体所致的马赫环

这一过程也可能持续很久，导致羽流内部压强再次低于环境压强。随着时间的推移，压缩和膨胀过程不断重复，排气中的气体压强和外部大气压强之间的差异逐渐减小，直到排气压强与环境大气压强相同。

飞机产生的马赫环

气体从可乐瓶中流出

马赫环的产生条件

超音速气流由于压力低于环境，会形成一道激波并被剧烈压缩。在这道激波压缩后，压力反而又高于了环境压力，会再形成膨胀波。然后再被压缩，再膨胀。循环下去，所以人能看到一道规律的钻石状马赫环。

也就是说只要喷出的超音速流体只要压力不等于环境压力，就会形成「膨胀 - 压缩 - 膨胀 - 压缩」的循环现象，唯一的区别是，第一道波是激波压缩还是直接膨胀。所以不管是哪种情况，看起来都差不多。

当尾流压力增加时，密度提高，速度变慢，总温不变而静温提高。也就是压力大的地方气就热了，且这时高温会更促使加力燃烧室喷出的未完全燃烧燃油再次燃烧，且本来气体温度的变化也会影响颜色。

马赫环产生装置

火箭升空

水下射击

马赫盘

这些现象都是由于驻波产生的结果，这导致在空间上形成一系列的节点与波腹。由于牛顿第三定律，施加的推动会产生相反的力，从而形成加压（波腹）和减压（波节）区域。

本期科普知识小总结

按性质来分主要有四种：机械波、电磁波、引力波、物质波。

机械波是由扰动的传播所导致的在物质中动量和能量的传输。一般的物体都是由大量相互作用着的质点所组成的，当物体的某一部分发生振动时，其余各部分由于质点的相互作用也会相继振动起来，物质本身没有相应的大块的移动。

例如，沿着弦或弹簧传播的波、声波、水波。我们称传播波的物质叫介质，它们是可形变的或弹性的和连绵延展的。对于电磁波或引力波，介质并不是必要的，传播的扰动不是介质的移动而是场 —— 前者电磁波是电磁场在空间中以波的形式移动，引力波是时空弯曲在空间中以波的形式移动。

量子力学认为，任何物质既有粒子性，又有波动性，即任何物质都具有波粒二象性，于是就有所谓的物质波（也称德布罗意波），如电子波、中子波等。

扩展资料：

波的形式是多种多样的。它赖以传播的空间可以是充满物质的，也可以是真空（对电磁波而言）。有些形式的波能为人们的感官所感觉，有些却不能。人们最熟悉的是水面波，它有几种类型。例如，在深水的表面，有主要以重力为恢复力的表面波，典型波长为 1m 到 100m；

有主要以表面张力为恢复力的涟波，波长约短于 0.07m。这两种波常具有正弦形状。在深水内部则有内重力波，出现在海洋内有密度分层的区域。

不只在海洋里，在大气层里，也可以出现内重力波。空气中更广泛遇到的，当然是声波。声波中传播的是空气中压强、密度等物理量的扰动，扰动指对无声波时原有值的偏离。

声学谐振器中的能量损失

Yang Yang 声物理世界 2024 年 04 月 10 日 19:51 湖南

1. 摘要

驻波是强非线性的，其在传播过程中伴随着谐波产生、共振频移和迟滞等现象。之前有学者已经建立了一维模型来分析声学谐振器中的高振幅驻波，但该模型唯一考虑到的衰减是由谐振器体积中的粘度引起的。然而大部分能量损失发生在沿腔壁的声边界层中，当需要精确计算能量耗散时，必须考虑边界层内的能量耗散。本文研究了边界层对腔内声场以及腔内能量耗散的影响，从线性近似下粘性流体边界层的动量方程出发，推出了谐振腔内部边界层中的能量耗散公式。（当然，除了边界层中的粘性衰减外，声波引发的湍流也会加速声能量的衰减，湍流所带来的影响可采用涡流粘性公式来模拟）。利用数值计算的手段对三种不同几何形状的谐振器（圆柱形、喇叭锥形、球型）分别给定不同的水平加速度，得出了压力波和速度波的谐波幅值分布、沿谐振腔轴线不同位置的压力和速度波的形状以及能量损耗情况。最后，以实验的手段，对所得理论结果进行验证，发现实测耗散与预测耗散两者吻合良好。

2. 结果展示

2.1 谐振器边界层声能耗散理论

线性近似下粘性流体边界层的动量方程为:

$\frac{\partial u_z}{\partial t} = v_0 \frac{\partial^2 u_z}{\partial y^2} - \frac{1}{\rho_0} \frac{\partial p}{\partial z}$

式中 $u_z$ 为粒子沿腔壁的速度分量； $p$ 为总压； $z$ 为沿腔壁的坐标； $y$ 为与腔壁垂直的坐标； $V_0 = \frac{h_0}{\rho_0}$ 为运动粘度系数，其中 $\rho_0$ 为气体的平衡密度， $\eta_0$ 为动力粘度。求解微分方程可得：

$u_z = \frac{1}{2} \sum_n u_n e^{in\omega t} + c.c.$

式中 $u_n$ 是速度波谐波分量的复幅值； $c . c .$ 是它们的复共轭。谐波速度分量的幅值由下式给出：

$u_n = u_n^{(0)} \left(1 - e^{-\alpha y}\right)$

$\large \alpha = \sqrt{\frac{in\omega\rho_0}{\eta_0}}$

上式中 $u_n^{(0)}$ 是平行于壁面的主流谐波速度，它代表边界层的源。速度已知，就可以计算出能量耗散。对于一维流体运动，单位时间和单位体积的能量耗散等于：

$\large q = \eta_0 \left(\frac{\partial u_z}{\partial y}\right)^2$

将 $u_z$ 代入上式，并求解散分方程可得边界层中能量损失方程为：

$\large W = \frac{\sqrt{2\eta_0\rho_0}}{4} \int_0^l \Sigma_n |\tilde{u}_n|^2 \sqrt{n\omega} 2\pi r \left(1 + r_1^2\right)^{\frac{3}{2}} d x$

式中 $r_1 = \frac{d r}{d x}$ ； $l$ 为谐振腔长度； $u_n$ 为一维模型得到的速度轴向分量；坐标 $r$ 是谐振器的半径。

从公式中可看出，谐振管半径越大，外界激励频率越高，管内边界层能量损失越多。

2.2 数值分析结果

(a) 圆柱形谐振器

(b) 锥形谐振器

© 球型谐振器

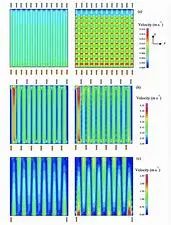
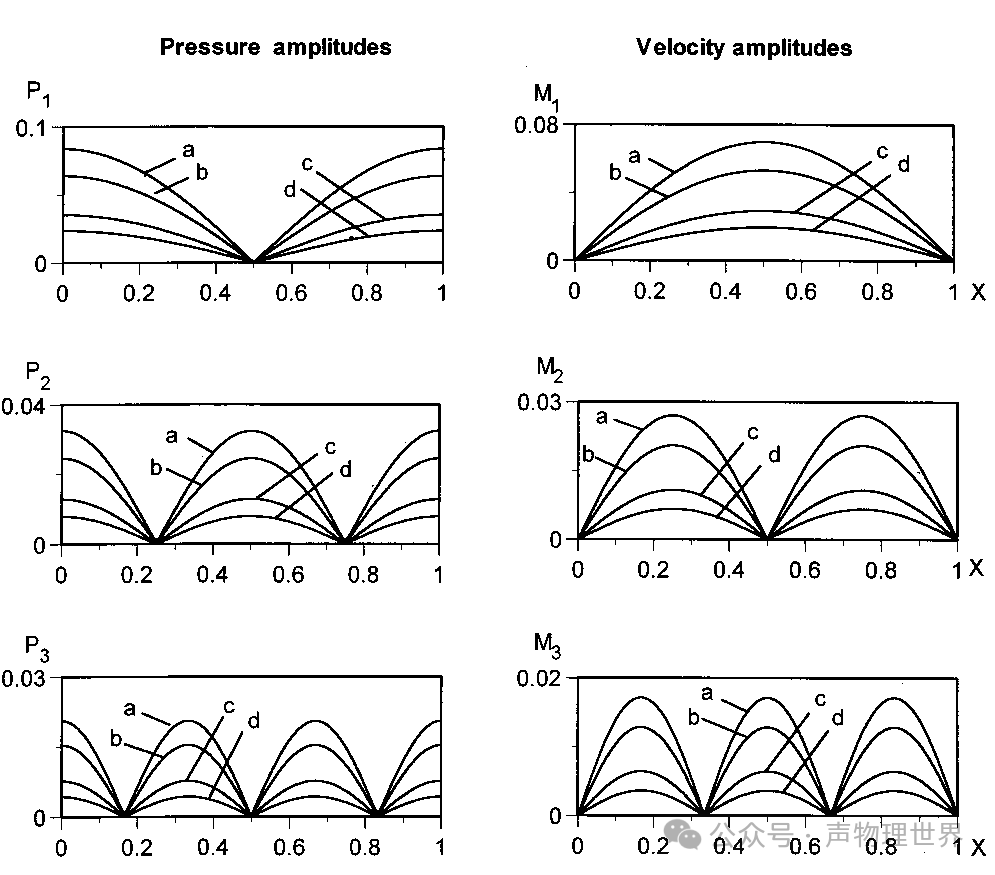
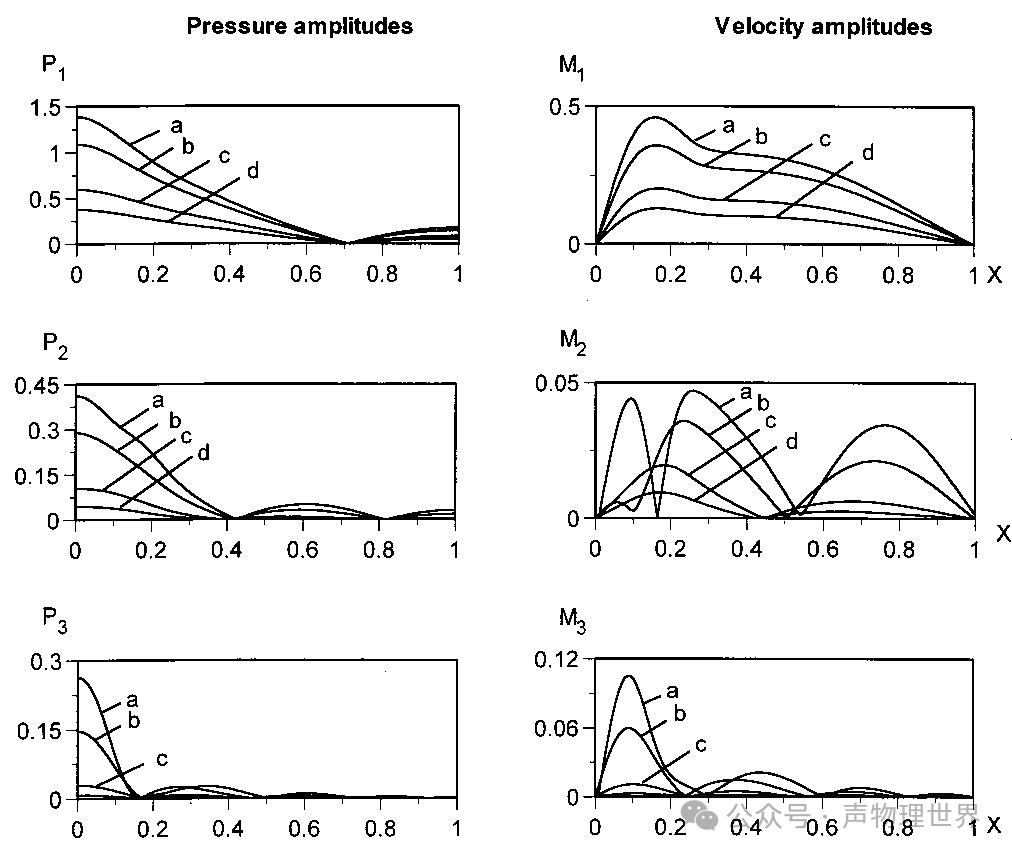
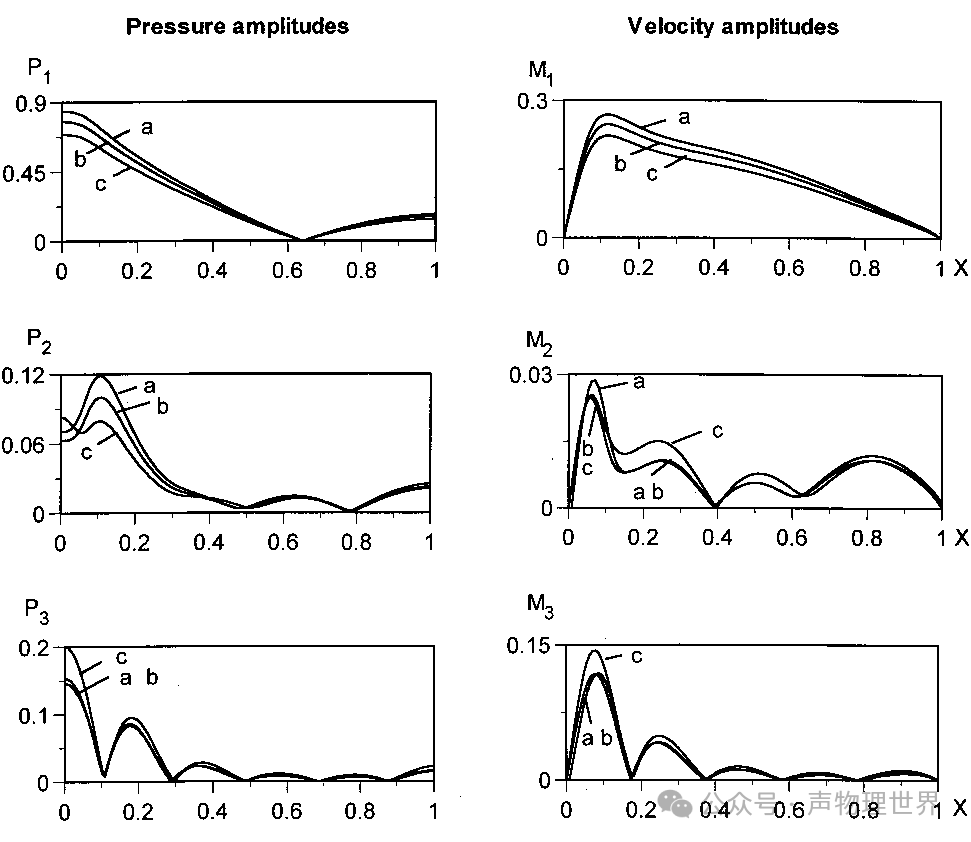
图 1 前三次谐波振幅沿谐振器内分布的压力波和粒子速度波

图 1 中不同加速度幅值如下：

$A=5\times10^{-4}$ (曲线 a)

$A=3\times10^{-4}$ (曲线 b)

$A=1\times10^{-4}$ (曲线 c)

$A=0.5\times10^{-4}$ (曲线 d)

其中，M1、M2、M3 为声速波经声速归一化后谐波幅值所对应的声马赫数，P1、P2、P3 为经环境压力归一化后对应的谐波声压。

图 1(a) 为圆柱形谐振器前三次谐波振幅沿圆柱形谐振器内的压力波和粒子速度波分布图（左图为压力波，右图为速度波）。图中所有曲线相对于 $x^*=0.5$ 都是对称的，对于所有加速度幅值，压力和速度节点都在同一位置且压力和速度幅值的最大值随加速度幅值的增大而增大。

喇叭锥形谐振腔的驻波特性与圆柱腔的驻波特性不同。图 1(b) 为锥形谐振器前三次谐波振幅沿谐振器内的压力波和粒子速度波分布图（左图为压力波，右图为速度波）。压力波的谐波幅值不再沿谐振腔轴对称，而是具有相同的一般行为，即基波为半波长，二次谐波为全波长，三谐波为一个半波长。在 $X = 0$ 时，当加速度达到最高水平时，基本压力幅值达到 1.25。一般来说，同样的观察结果也适用于速度分布。然而，对于高加速水平，在最高的加速度水平下，压力波的三次谐波幅值与第二次谐波幅值相同，速度波的三次谐波幅值大于第二次谐波幅值，二次和三次谐波分布中的节点向更高的 $x$ 值偏移。

(a) 圆柱形谐振器

(b) 锥形谐振器

© 球型谐振器

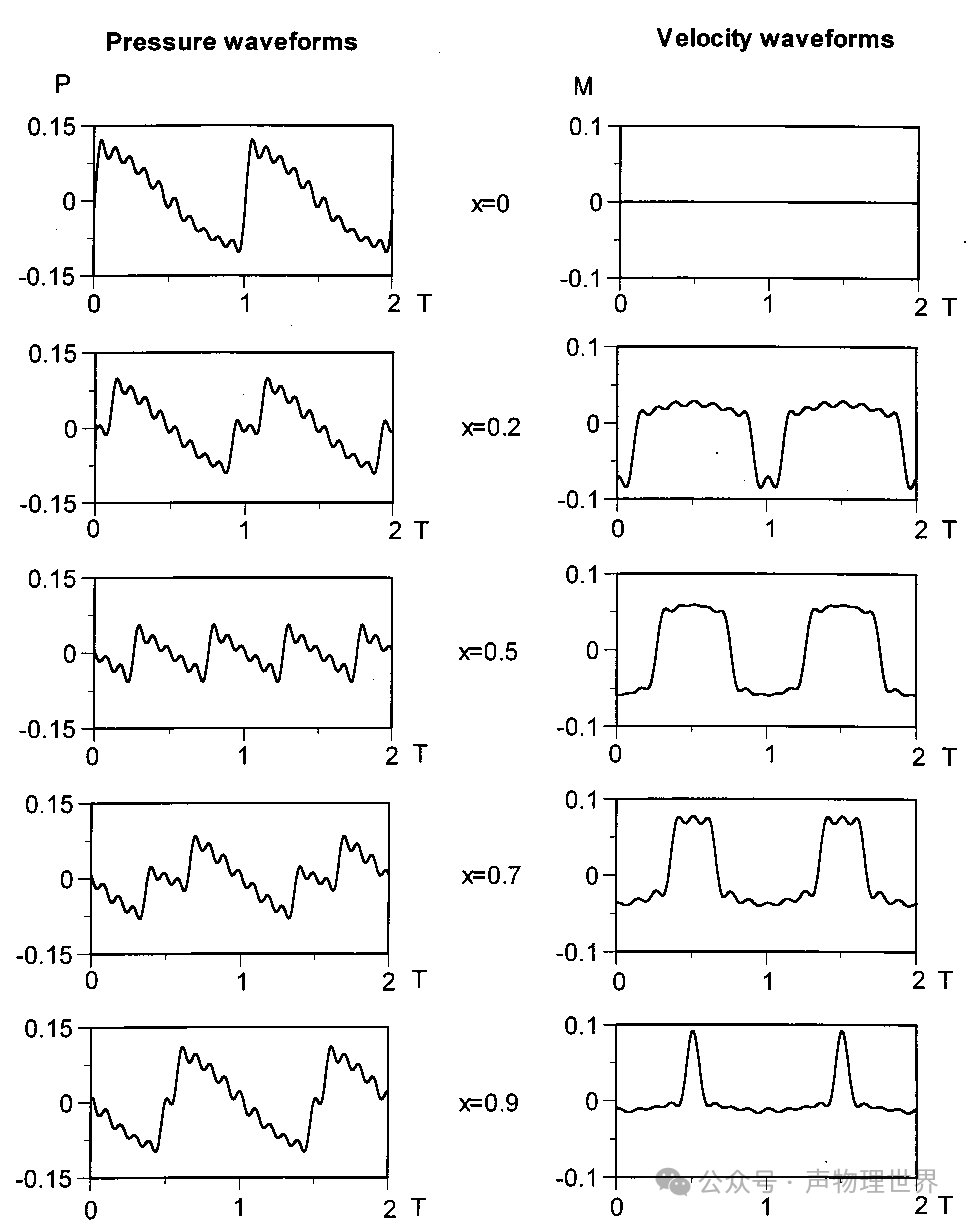
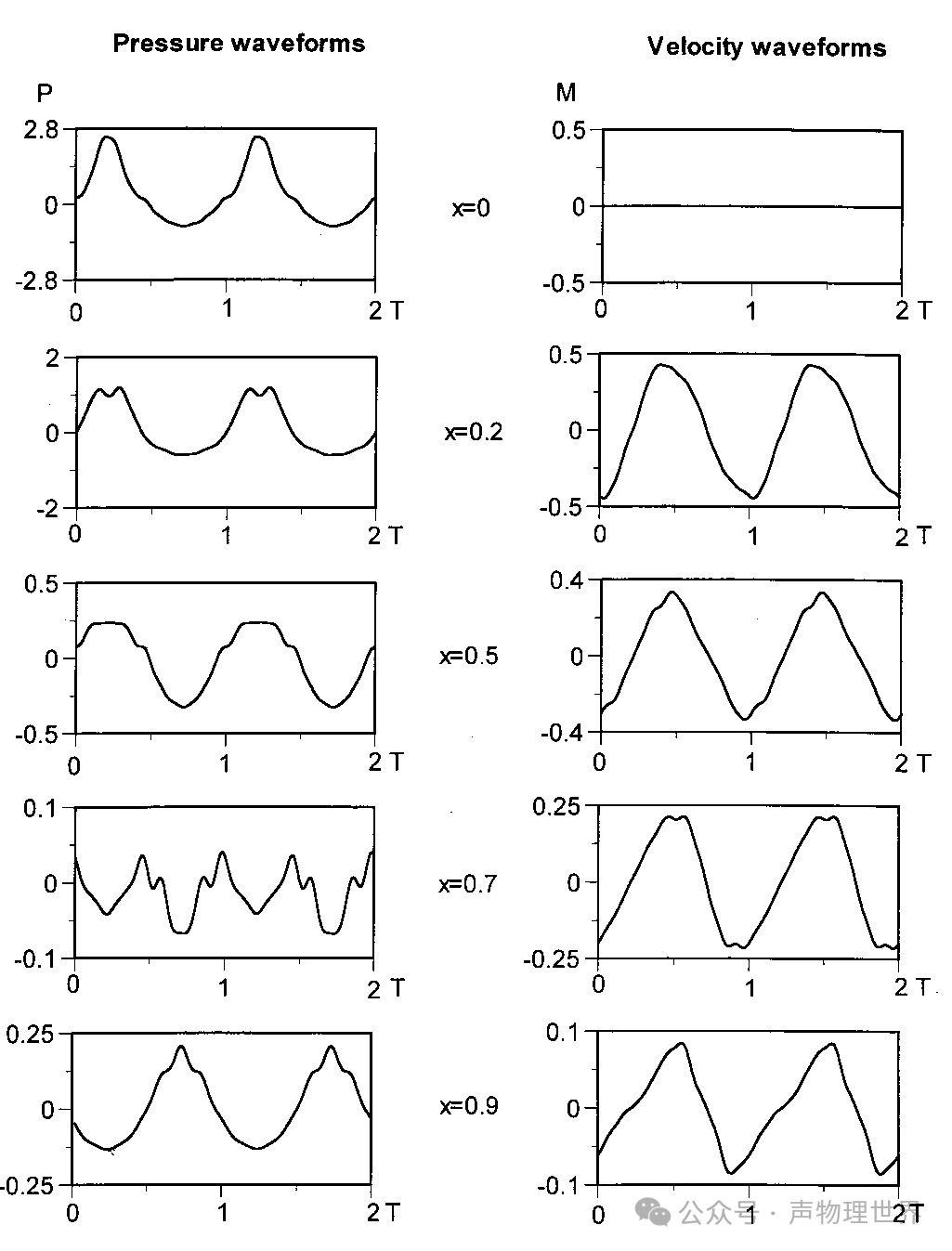
图 2 谐振器的不同位置压力波波形 (左栏) 和速度波波形 (右列) 随时间的变化趋势

图 2 中加速度幅值 $A=5\times10^{-4}$ ； $\Omega=\frac{\omega}{\omega_0}=1$ ，其中 $\omega$ 为声源发声频率； $\omega_0$ 为圆柱形谐振管的固有频率； $M$ 为马赫数； $P$ 为无因次声压； $T$ 为周期。

图 2 (a) 为圆柱谐振器的不同位置压力波波形 (左栏) 和速度波波形 (右列) 随时间的变化趋势图。图 2 (a) 显示了波在圆柱谐振器中的强烈非线性畸变，激波锋面既存在于粒子速度波中，也存在于压力波中。速度波的形状与压力波的形状不同，在 $X = 0$ 时，压力波形具有经典的锯齿形。在谐振腔的中间 $X = 0.5$ ，此时频率是基波的两倍，最大压力幅值约 0.10。在谐振腔中部，速度波的形状为方波，而在端壁附近，速度波的形状更接近于脉冲函数，最大速度幅值约为 0.1。

图 2 (b) 为锥形谐振器的不同位置压力波波形 (左栏) 和速度波波形 (右列) 随时间的变化趋势图。从图 2 (b) 中也可以清楚地看出，锥形谐振器中谐波的产生被抑制，谐波相位被改变，从而防止了激波的形成。 在 $X = 0$ 时，喇叭锥体的压力波形为 u 型波形，即形成了更陡的峰和更宽的谷。速度波形一般呈三角形波形。最大压力幅值约为 2.5，最大速度幅值约为 0.5。压力和速度波形如图 7 所示。在压力波或速度波中未观察到冲击波。

(a) 圆柱形谐振器

(b) 锥形谐振器

© 球型谐振器

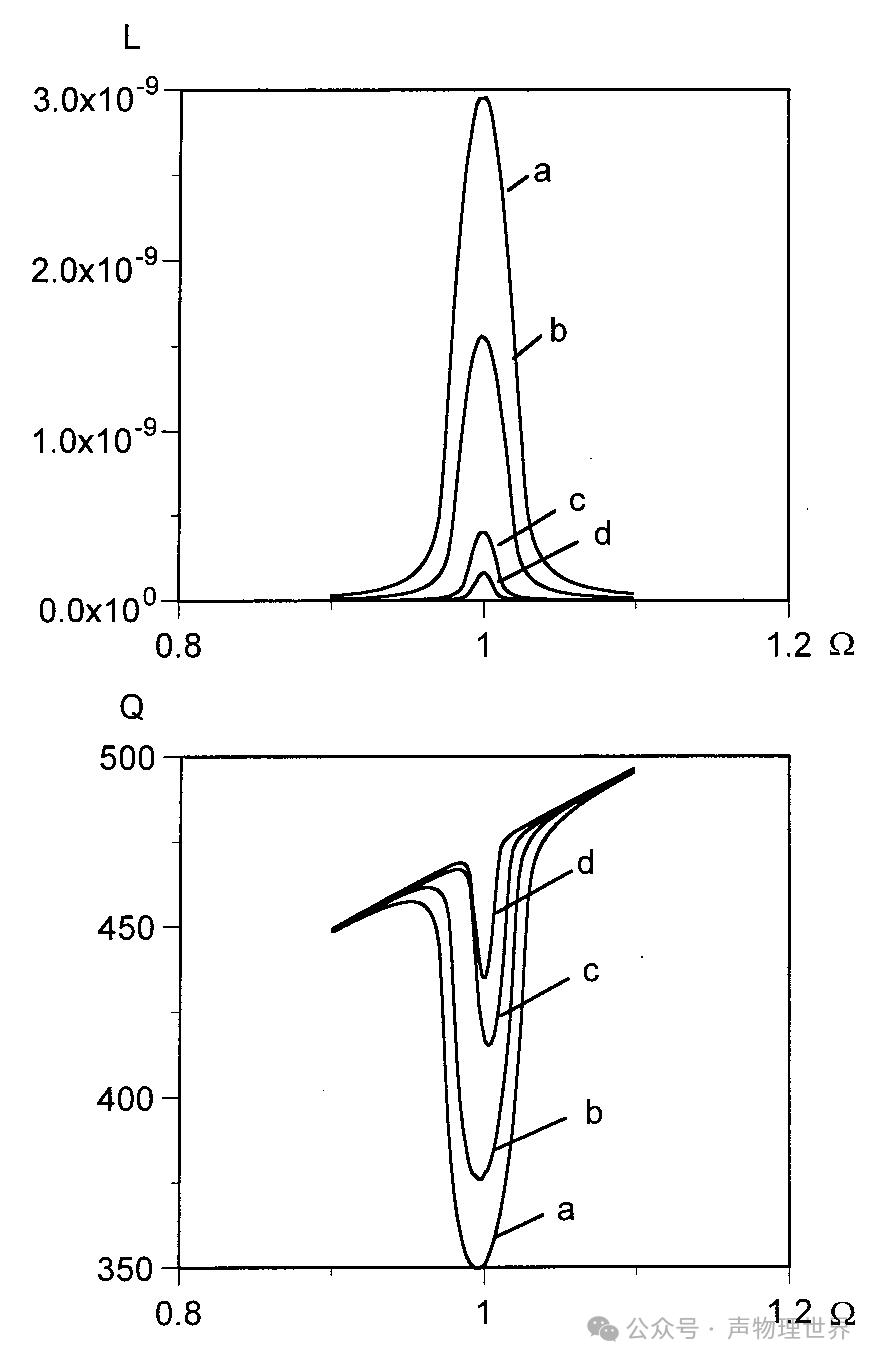
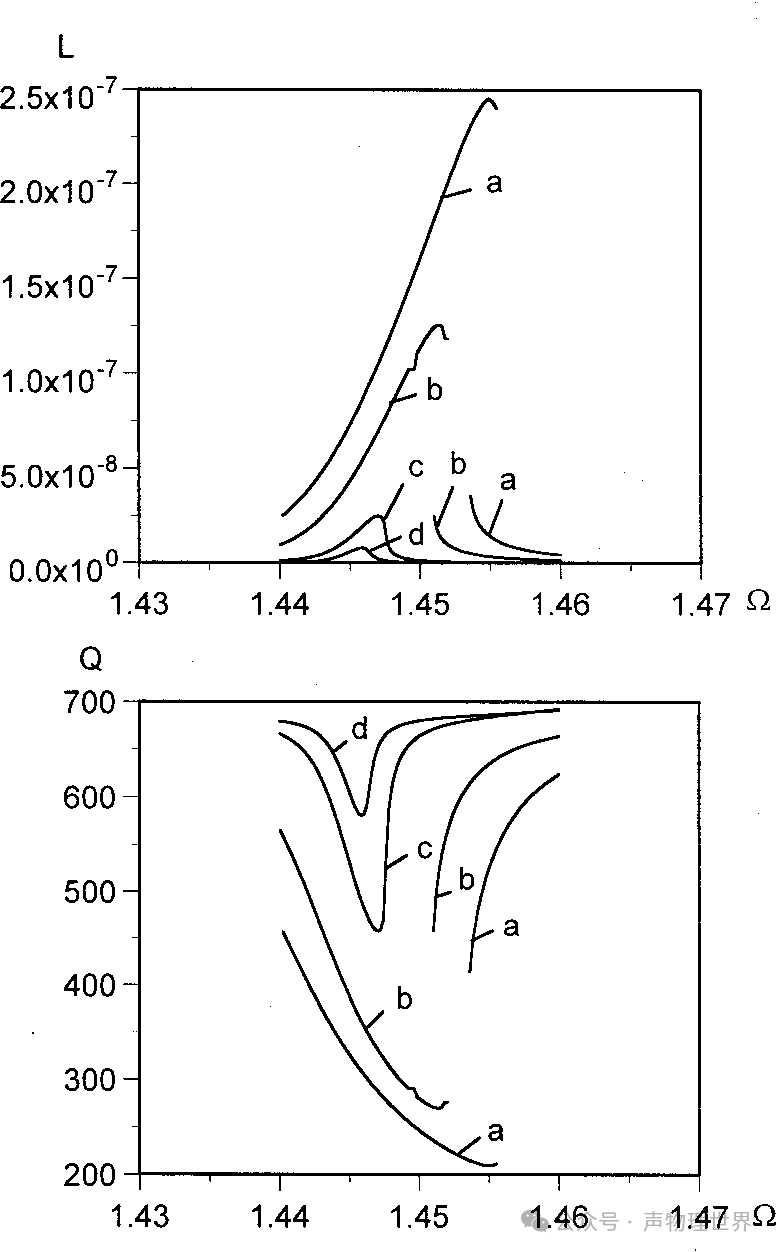
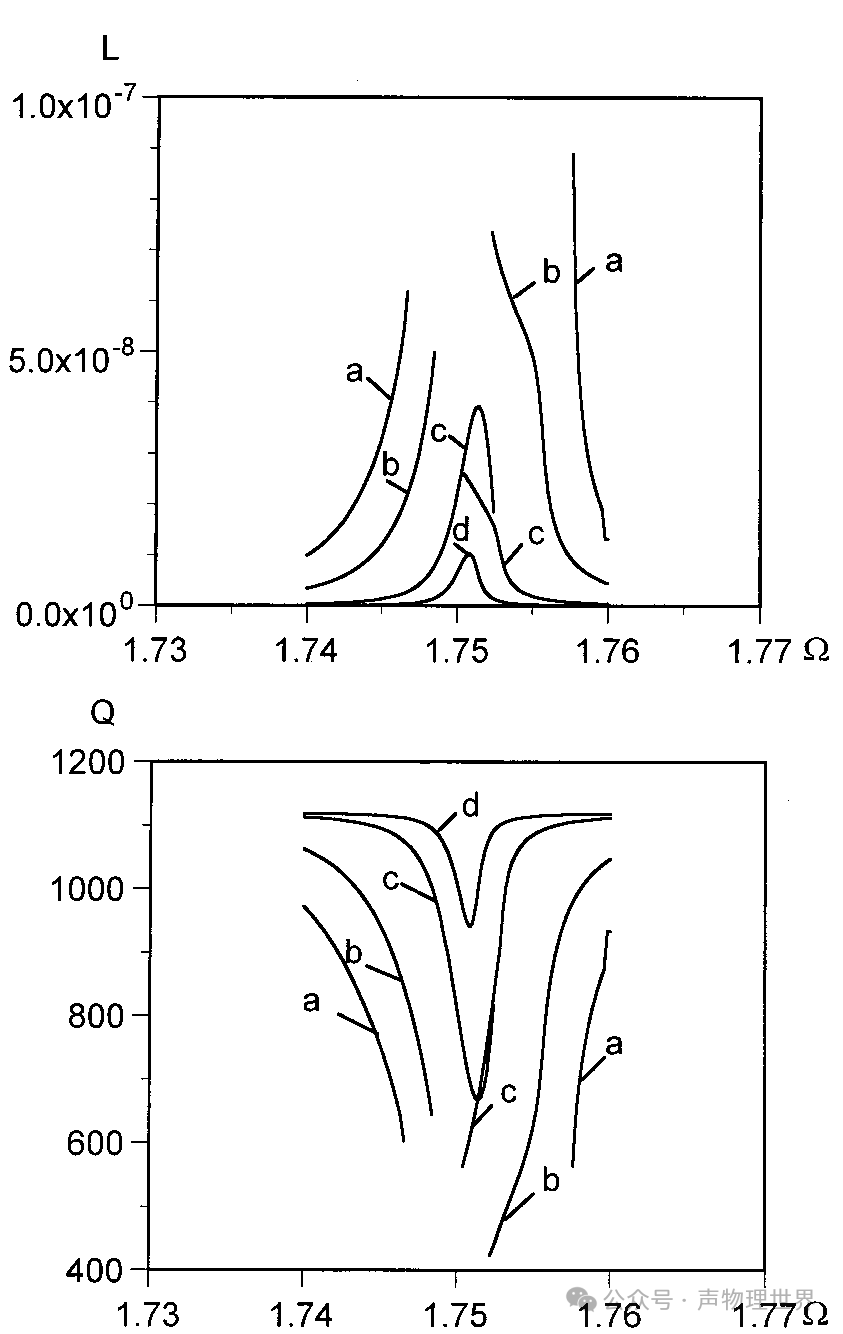
图 3 不同加速度幅值下强声波在谐振管中的能量损失

图 3 中不同曲线的加速度幅值 $A=5\times10^{-4}$ (曲线 a)， $A=3\times10^{-4}$ (曲线 b)， $A=1\times10^{-4}$ (曲线 c)，和 $A=0.5\times10^{-4}$ (曲线 d)。

圆柱形谐振器能量损失如图 3 (a) 所示。曲线显示出共振行为，能量损失在 $\Omega=1$ 处达到最大值。能量损失随着加速度振幅的增加而增加。

2.3 实验验证

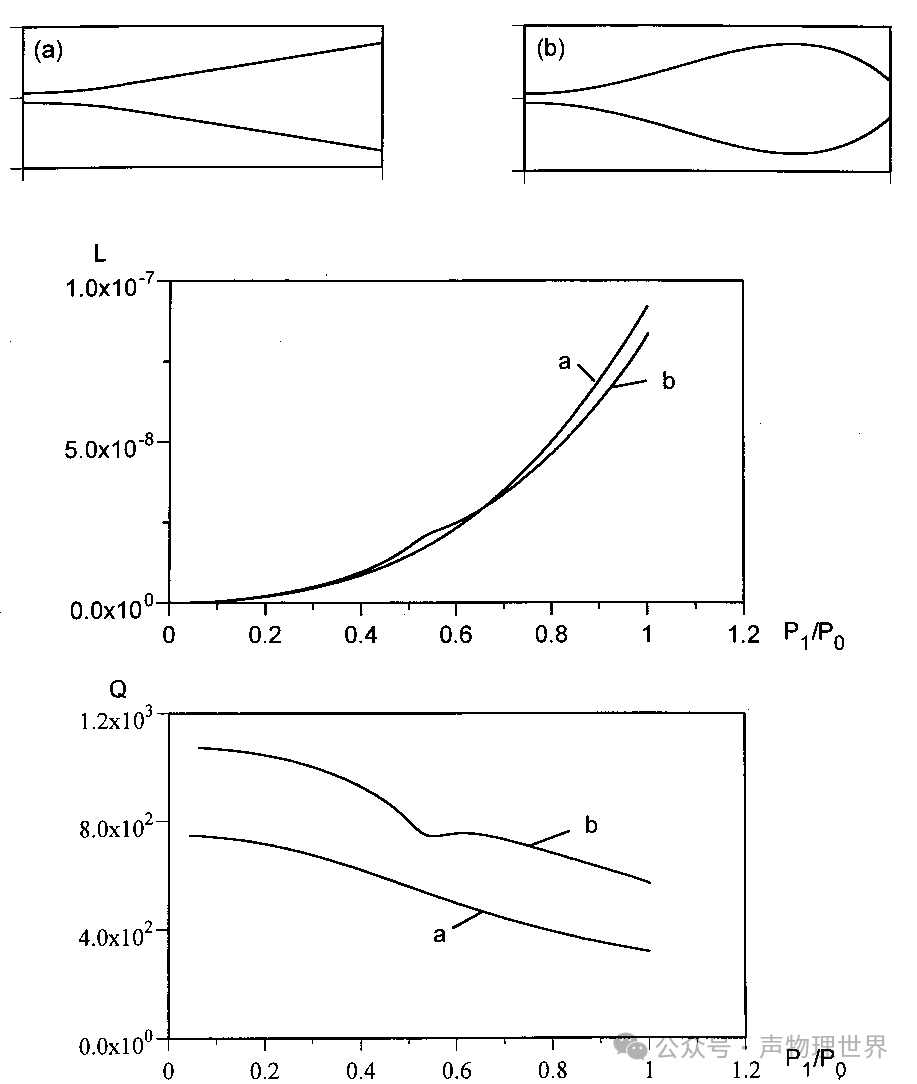
图 4 基波压力振幅对两种谐振器的能量损失影响

图 4 给出了两种谐振器的能量损失 L 随基本压力幅值的变化关系，一种是锥形 (曲线 a) 和一种是球型 (曲线 b)。谐振器的形状也被显示出来。**两种谐振器能量损失趋势大致相同，均随着入射波压力的增加而增加，且同等压力幅值下喇叭锥形谐振器的能量损耗更多。**这个例子说明了谐振器的几何形状可以显著地改变驻波的特性。

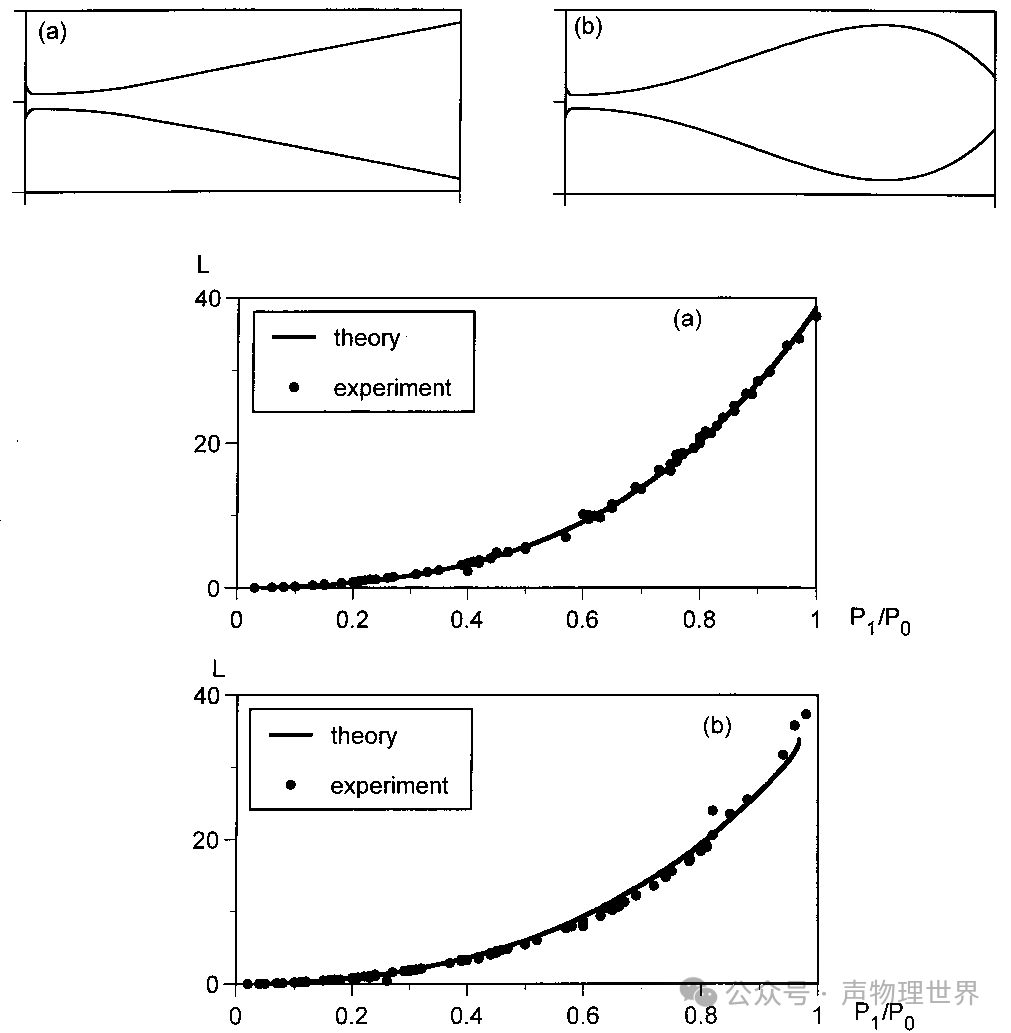
图 5 两种谐振腔的实验数据与理论预测的比较

（ $P_0=2.72 \, \text{bar}; \quad T_0=327 \, \text{K}$ ）

如图 5 对锥形和球型谐振腔的实验数据与理论预测的比较，即将谐振器中预测的能量损失曲线与能量损失的实测值相匹配，发现边界层能量损失的理论预测与实验结果吻合较好。谐振器的几何形状如图 5 顶部所示。

3. 结论

（1）建立了一维数学模型来分析轴对称谐振器中的非线性驻波。对以往的模型进行了修正，加入了沿腔壁的声边界层的影响，引入了边界层能量损失，影响了谐振腔内的声场。

（2）对三种谐振器：圆柱、喇叭锥形和球型谐振器进行数值分析。通过给定谐振器 4 种不同水平的加速度，得出了压力波和速度波的谐波幅值分布、沿谐振腔轴线在不同位置计算得到的压力和速度波形、能量损耗随频率的变化规律。发现圆柱形谐振腔的压力波形在压力非常有限的情况下表现为典型的锯齿波形，即形成了激波；而喇叭锥形谐振腔和球型谐振腔中由于谐波的产生被抑制，谐波相位被改变，从而防止了激波的形成，使得压力波形不受影响。在相同的加速度水平下，锥形谐振器可以获得更高的压力，其次是球型谐振器，最后为圆柱形谐振器。腔内能量损失方面，在同等条件下锥形谐振器损失的能量最多，其次为球型谐振器，圆柱形谐振器能量损失最少。

（3）给出了喇叭锥形和球型两种谐振器能量损失的数值与实验结果的比较，数值计算得到的能量损失与实验数据吻合较好。

4. 参考文献

Ilinskii Yurii A, Bart Lipkens, Evgenia A Zabolotskaya. Energy losses in an acoustical resonator [J]. The Journal of the Acoustical Society of America 109.5 (2001): 1859-1870.

原创钟锡华 Optics4All

知识点

惠更斯原理

1 原理内容

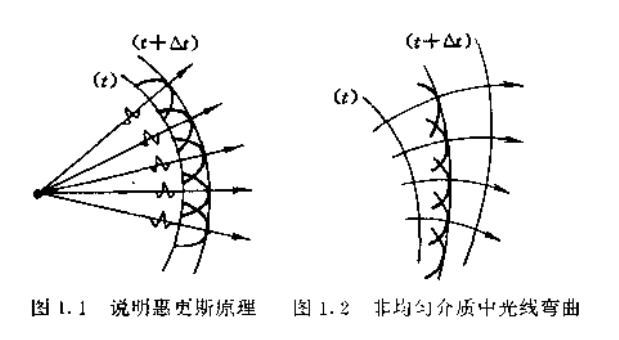
距今三百多年前，惠更斯提出了一个关于光波传播的理念，如图 1.1 所示，其大意如下：光扰动同时到达的空间曲面被称为波面或波前，波前上的每一点可以被看作一个新的扰动中心，称其为子波源或次波源，次波源向四周激发次波；下一时刻的波前应当是这些大量次波面的公共切面，也称其为包络面：次波中心与其次波面上的那个切点的连线方向，给出了该处光传播方向，亦即光射线方向。根据惠更斯原理，人们可以由某一时刻 (t) 的波前，用作图法导出下一时刻

的波前，并确定波前上各点的光射线。这就是说，该原理解决了波前随时间在空间的传播问题。图 1.2 显示了光在非均匀介质中波前的推移以及相应的光线弯曲，在这里上方介质中的波速大，下方介质中的波速小.

2 评价

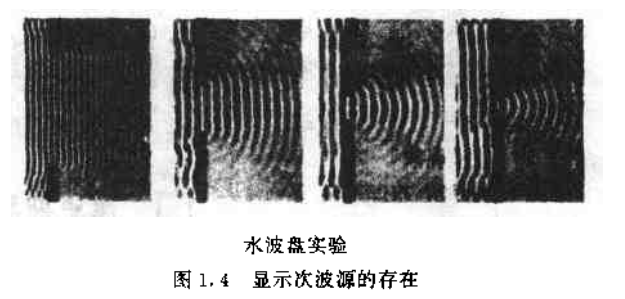
惠更斯 (Christian Huygens,1629-1695), 荷兰物理学家、天文学家和数学家，青年时期与 R, 笛卡尔 (1596-1650) 等学界名流交往甚密，他在 1679 年向法国科学院的报告，和 1690 年出版的《论光》中，提出了光的波动理论，从几何学上给出了寻求光传播方向的普遍方法 – 被后人演绎并命名为惠更斯原理，如前面所述，惠更斯原理毕竟是历史上第一个关于波传播的原理，自然地有着许多重大的不足，比如，它不能回答光振幅或光强度的传播问题，它也不能回答光相位的传播问题，这是因为当时在惠更斯关于光波动的论述中，尚无空间周期性概念，即尚无光波长概念，对这些问题的进一步研究最终导致了光波射理论的形成。然而，惠更斯原理的精华是其次波概念 – 波场中的任意一点均可以被看作一个点源，它具有永恒的科学价值，至今依然被不时地引用，且适用于一切波场，包括光波、声波、水波，等等，图 1.4 是一张水波盘实验照片，在浅水表面波传播的前方，设置一个狭缝；当狭缝足够窄时，凸显出狭缝小孔处成为一个次波源，以此为中心向前激发一个发散型波前.

如何理解惠更斯原理？

天天可以吃物理小识

如果将一块石头投入水中，会激起一圈圈由中心向四周扩散的水波。那么，水波如果遇上树墩之类的障碍物，或者从池壁处反射回来，它的运动方式应该是怎样的呢？1690 年，荷兰物理学家惠更斯给出了他对以上问题的解释 —— 惠更斯原理。

该原理指出：波阵面上的每个点都可以看作新的波源，这些新的波源向四面八方发出次级子波，经过一定时间之后，这些子波的包络面就构成了下一时刻的波面。

我们可以这样理解惠更斯原理，在上面问题的情境中，假设我们可以把圆环形的波在某一时刻固定住，那么就可以将波上的每一个点视为一个新波的波源，而且这些波源所产生的波与固定住的圆环形波具有相同的频率和相位。就好像将一圈石子按照被固定住的波纹的形状同时扔到水中，所形成的波纹又成为下一组波源传播能量的起点。多次重复，应用这个方法就可以得到水波扩散的轨迹。这就是惠更斯原理的基本思想。

惠更斯原理可用来证明光的反射定律和折射定律，也可用来解释晶体中的双折射现象。不过，惠更斯原理只能解决波在媒质中传播的方向问题，却不能解决强度分布问题。

via：

怎样优雅地画驻波模型图和惠更斯原理图？ 原创薛德堡物含妙理 2024 年 09 月 28 日 17:42 广东
https://mp.weixin.qq.com/s/w1f9KnGNWHmQ0zw5FGWa_g
关于惠更斯原理图画法的一点补充 原创薛德堡物含妙理 2024年09月29日 00:18 广东
https://mp.weixin.qq.com/s/1ryh1vK_aSCHPLAjNGwq3A
驻波，有趣而常见的自然现象 东软物理社团 2022年04月15日 10:42
https://mp.weixin.qq.com/s/ef_gPG0bXadIZDL23SXWhw
声学谐振器中的能量损失 Yang Yang 声物理世界 2024年04月10日 19:51 湖南
https://mp.weixin.qq.com/s/jFhg8TcRrzDxwz-k6YTxUw
如何理解惠更斯原理？天天可以吃物理小识 2022 年 04 月 23 日 08:00
https://mp.weixin.qq.com/s/NTeWQoiSPmVe3IcygrTYPg
光学原理回顾：惠更斯－菲涅耳原理 - 知乎 法海伊尔默瑙工业大学员工编辑于 2023-08-14 15:18・IP 属地德国
https://zhuanlan.zhihu.com/p/339379109