注:本文为 “比特、字节与布尔逻辑” 相关文章合辑。
英文引文,机翻未校。
How Bits and Bytes Work
位和字节的工作原理
By: Marshall Brain
If you have used a computer for more than five minutes, then you have heard the words bits and bytes. Both RAM and hard disk capacities are measured in bytes, as are file sizes when you examine them in a file viewer.
如果你使用电脑的时间超过五分钟,那么你肯定听说过“位”(bits)和“字节”(bytes)这两个词。无论是 RAM 还是硬盘的容量,都是以字节为单位来衡量的,当你在文件查看器中查看文件大小时,同样也是以字节为单位。
You might hear an advertisement that says, “This computer has a 32-bit Pentium processor with 64 megabytes of RAM and 2.1 gigabytes of hard disk space.” Many HowStuffWorks articles talk about bytes (for example, How CDs Work). In this article, we will discuss bits and bytes so that you have a complete understanding.
你可能会听到一则广告说:“这台电脑配备了一个 32 位 的奔腾处理器,拥有 64 兆字节 的 RAM 和 2.1 吉字节 的硬盘空间。”许多 HowStuffWorks 的文章也都会谈到字节(例如,光盘的工作原理)。在本文中,我们将讨论位和字节,以便您能够完全理解它们。
Decimal Numbers
十进制数字
The easiest way to understand bits is to compare them to something you know: digits. A digit is a single place that can hold numerical values between 0 and 9. Digits are normally combined together in groups to create larger numbers. For example, 6,357 has four digits. It is understood that in the number 6,357, the 7 is filling the “1s place,” while the 5 is filling the 10s place, the 3 is filling the 100s place and the 6 is filling the 1,000s place. So you could express things this way if you wanted to be explicit:
理解位的最简单方法是将其与你熟悉的东西进行比较:数字(digits)。一个数字是一个可以容纳 0 到 9 之间数值的单个位置。通常,数字会组合在一起形成更大的数字。例如,6357 有四个数字。在数字 6357 中,7 位于“个位”,5 位于十位,3 位于百位,6 位于千位。因此,如果你想要明确地表示,可以这样表达:
( 6 × 1000 ) + ( 3 × 100 ) + ( 5 × 10 ) + ( 7 × 1 ) = 6000 + 300 + 50 + 7 = 6357 (6 \times 1000) + (3 \times 100) + (5 \times 10) + (7 \times 1) = 6000 + 300 + 50 + 7 = 6357 (6×1000)+(3×100)+(5×10)+(7×1)=6000+300+50+7=6357
Another way to express it would be to use powers of 10. Assuming that we are going to represent the concept of “raised to the power of” with the “^” symbol (so “10 squared” is written as “
1
0
2
10^2
102”), another way to express it is like this:
另一种表达方式是使用 10 的幂。假设我们用“^”符号来表示“乘方”这个概念(所以“10 的平方”写作“
1
0
2
10^2
102”),另一种表达方式如下:
( 6 × 1 0 3 ) + ( 3 × 1 0 2 ) + ( 5 × 1 0 1 ) + ( 7 × 1 0 0 ) = 6000 + 300 + 50 + 7 = 6357 (6 \times 10^3) + (3 \times 10^2) + (5 \times 10^1) + (7 \times 10^0) = 6000 + 300 + 50 + 7 = 6357 (6×103)+(3×102)+(5×101)+(7×100)=6000+300+50+7=6357
What you can see from this expression is that each digit is a placeholder for the next higher power of 10, starting in the first digit with 10 raised to the power of zero.
从这个表达式中,你可以看出每个数字都是下一个更高 10 的幂的 占位符,从第一个数字开始,10 的幂为零。
That should all feel pretty comfortable – we work with decimal digits every day. The neat thing about number systems is that there is nothing that forces you to have 10 different values in a digit. Our base-10 number system likely grew up because we have 10 fingers, but if we happened to evolve to have eight fingers instead, we would probably have a base-8 number system. You can have base-anything number systems. In fact, there are lots of good reasons to use different bases in different situations.
这些内容应该会让你感觉很熟悉——我们每天都在使用十进制数字。关于数字系统的一个有趣之处在于,并没有什么东西强制你在一个数字中必须有 10 个不同的值。我们的 十进制 数字系统之所以存在,很可能是因为我们有 10 个手指,但如果我们在进化过程中恰好有 8 个手指,那么我们可能就会有一个八进制的数字系统。你可以有任意基数的数字系统。实际上,在不同的情境下使用不同的基数有很多很好的理由。
Computers happen to operate using the base-2 number system, also known as the binary number system (just like the base-10 number system is known as the decimal number system). Find out why and how that works in the next section.
计算机碰巧使用的是二进制数字系统(也称为 二进制数系统,就像十进制数字系统被称为十进制数系统一样)。在下一节中,我们将了解其原因以及它是如何工作的。
The Base-2 System and the 8-bit Byte
二进制系统和 8 位字节
The reason computers use the base-2 system is because it makes it a lot easier to implement them with current electronic technology. You could wire up and build computers that operate in base-10, but they would be fiendishly expensive right now. On the other hand, base-2 computers are relatively cheap.
计算机使用二进制系统的原因是,利用当前的电子技术实现起来要容易得多。你当然可以搭建并制造出以十进制为基础运行的计算机,但目前来说,那将是极其昂贵的。另一方面,二进制计算机相对来说比较便宜。
So computers use binary numbers, and therefore use binary digits in place of decimal digits. The word bit is a shortening of the words “Binary digIT.” Whereas decimal digits have 10 possible values ranging from 0 to 9, bits have only two possible values: 0 and 1. Therefore, a binary number is composed of only 0s and 1s, like this: 1011. How do you figure out what the value of the binary number 1011 is? You do it in the same way we did it above for 6357, but you use a base of 2 instead of a base of 10. So:
所以计算机使用二进制数,因此用 二进制位 替代了十进制位。单词 bit 是“二进制位”(Binary digIT)的简写。与有 10 种可能的值(从 0 到 9)的十进制位不同,二进制位只有两种可能的值:0 和 1。因此,一个二进制数只由 0 和 1 组成,例如:1011。那么,如何计算二进制数 1011 的值呢?方法与上面计算 6357 时相同,只是用 2 作为基数,而不是 10。所以:
( 1 × 2 3 ) + ( 0 × 2 2 ) + ( 1 × 2 1 ) + ( 1 × 2 0 ) = 8 + 0 + 2 + 1 = 11 (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (1 \times 2^0) = 8 + 0 + 2 + 1 = 11 (1×23)+(0×22)+(1×21)+(1×20)=8+0+2+1=11
You can see that in binary numbers, each bit holds the value of increasing powers of 2. That makes counting in binary pretty easy. Starting at zero and going through 20, counting in decimal and binary looks like this:
你可以看到,在二进制数中,每个位代表 2 的幂。这使得二进制计数变得相当简单。从 0 开始到 20,十进制和二进制的计数如下:
0 = 0
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 = 1001
10 = 1010
11 = 1011
12 = 1100
13 = 1101
14 = 1110
15 = 1111
16 = 10000
17 = 10001
18 = 10010
19 = 10011
20 = 10100
From this sequence, you can see that 0 and 1 are the same in both the decimal and binary number systems. The first time you see a carry-over in the binary system is with the number 2. If a binary bit is 1 and you add 1 to it, then the bit becomes 0 and the next bit becomes 1. This carries through for the transition from 15 to 16, where the effect ripples through four bits, turning 1111 into 10000.
从这个序列中,你可以看到 0 和 1 在十进制和二进制数字系统中是相同的。在数字 2 时,你首次看到二进制系统中的进位现象。如果一个二进制位是 1,而你再给它加 1,那么这个位就会变成 0,而下一个位就会变成 1。在从 15 到 16 的转换过程中,这种效应会通过 4 个位传递,将 1111 变成 10000。
Bits are rarely seen alone in computers. They are almost always bundled together into 8-bit collections, and these collections are called bytes. Why are there 8 bits in a byte? A similar question is, “Why are there 12 eggs in a dozen?” The 8-bit byte is something that people settled on through trial and error over the past 50 years.
在计算机中,二进制位很少单独出现。它们几乎总是被捆绑成 8 位的组合,这些组合被称为 字节。为什么一个字节有 8 位呢?一个类似的问题是:“为什么一打有 12 个鸡蛋?”8 位字节是人们在过去 50 年中通过反复试验达成的共识。
With 8 bits in a byte, you can represent 256 values ranging from 0 to 255, as shown here:
在 8 位字节中,你可以表示从 0 到 255 的 256 个值,如下所示:
0 = 00000000
1 = 00000001
2 = 00000010
...
254 = 11111110
255 = 11111111
In the article How CDs Work, you learn that a CD uses 2 bytes, or 16 bits, per sample. That gives each sample a range from 0 to 65,535, like this:
在文章 光盘的工作原理 中,你了解到光盘每采样使用 2 个字节,即 16 位。这使得每个采样的范围从 0 到 65535,如下所示:
0 = 0000000000000000
1 = 0000000000000001
2 = 0000000000000010
...
65534 = 1111111111111110
65535 = 1111111111111111
Next, we’ll look at one way that bytes are used.
接下来,我们将探讨字节的一种使用方式。
The Standard ASCII Character Set
标准 ASCII 字符集
Bytes are frequently used to hold individual characters in a text document. In the ASCII character set, each binary value between 0 and 127 is given a specific character. Most computers extend the ASCII character set to use the full range of 256 characters available in a byte. The upper 128 characters handle special things like accented characters from common foreign languages.
字节经常被用来在文本文件中存储单个字符。在 ASCII 字符集 中,0 到 127 之间的每个二进制值都被赋予了一个特定的字符。大多数计算机扩展了 ASCII 字符集,以使用字节中可用的全部 256 个字符。上部的 128 个字符用于处理一些特殊字符,比如常见外语中的带重音字符。
You can see the 127 standard ASCII codes below. Computers store text documents, both on disk and in memory, using these codes. For example, if you use Notepad in Windows 95/98 to create a text file containing the words, “Four score and seven years ago,” Notepad would use 1 byte of memory per character (including 1 byte for each space character between the words – ASCII character 32). When Notepad stores the sentence in a file on disk, the file will also contain 1 byte per character and per space.
你可以看到下面的 127 个标准 ASCII 码。计算机使用这些代码在 磁盘 和 内存 中存储文本文件。例如,如果你在 Windows 95/98 中使用记事本创建一个包含“Four score and seven years ago”这句话的文本文件,记事本将为每个字符(包括每个单词之间的空格字符——ASCII 字符 32)使用 1 个字节的内存。当记事本将这句话存储在磁盘上的文件中时,文件也将包含每个字符和每个空格 1 个字节。
Try this experiment: Open up a new file in Notepad and insert the sentence, “Four score and seven years ago” in it. Save the file to disk under the name getty.txt. Then use the explorer and look at the size of the file. You will find that the file has a size of 30 bytes on disk: 1 byte for each character. If you add another word to the end of the sentence and re-save it, the file size will jump to the appropriate number of bytes. Each character consumes a byte.
尝试这个实验:在记事本中打开一个新文件,并输入“Four score and seven years ago”这句话。将文件以 getty.txt 的名称保存到磁盘上。然后使用资源管理器查看文件的大小。你会发现文件在磁盘上的大小为 30 个字节:每个字符 1 个字节。如果你在句子的末尾再添加一个单词并重新保存,文件大小将跳到相应的字节数。每个字符占用一个字节。
If you were to look at the file as a computer looks at it, you would find that each byte contains not a letter but a number – the number is the ASCII code corresponding to the character (see below). So on disk, the numbers for the file look like this:
如果你像计算机一样查看文件,你会发现每个字节包含的不是一个字母,而是一个数字——这个数字是与字符对应的 ASCII 码(见下文)。因此,在磁盘上,文件的数字如下所示:
F o u r a n d s e v e n
70 111 117 114 32 97 110 100 32 115 101 118 101 110
By looking in the ASCII table, you can see a one-to-one correspondence between each character and the ASCII code used. Note the use of 32 for a space – 32 is the ASCII code for a space. We could expand these decimal numbers out to binary numbers (so 32 = 00100000) if we wanted to be technically correct – that is how the computer really deals with things.
通过查看 ASCII 表,你可以看到每个字符与所使用的 ASCII 码之间的一一对应关系。注意空格使用的是 32——32 是空格的 ASCII 码。如果我们想在技术上做到完全正确,我们可以将这些十进制数字扩展为二进制数字(所以 32 = 00100000)——这确实是计算机真正处理事物的方式。
The first 32 values (0 through 31) are codes for things like carriage return and line feed. The space character is the 33rd value, followed by punctuation, digits, uppercase characters and lowercase characters. To see all 127 values, check out Unicode.org’s chart.
前 32 个值(0 到 31)是回车和换行等字符的代码。空格字符是第 33 个值,后面跟着的是标点符号、数字、大写字母和小写字母。要查看全部 127 个值,请查看 Unicode.org 的图表。
We’ll learn about byte prefixes and binary math next.
接下来,我们将学习字节前缀和二进制数学。
Byte Prefixes and Binary Math
字节前缀和二进制数学
When you start talking about lots of bytes, you get into prefixes like kilo, mega and giga, as in kilobyte, megabyte and gigabyte (also shortened to K, M and G, as in Kbytes, Mbytes and Gbytes or KB, MB and GB). The following table shows the binary multipliers:
当我们将话题转向大量的字节时,就会用到诸如千(kilo)、兆(mega)和吉(giga)这样的 前缀,就像在千字节(kilobyte)、兆字节(megabyte)和吉字节(gigabyte)中一样(也可以简写为 K、M 和 G,如 Kbytes、Mbytes 和 Gbytes 或 KB、MB 和 GB)。下表显示了 二进制 的乘数:
| 乘数名称 | 符号 | 进制 | 值 |
|---|---|---|---|
| Kilo | K | 2 10 2^{10} 210 | 1,024 |
| Mega | M | 2 20 2^{20} 220 | 1,048,576 |
| Giga | G | 2 30 2^{30} 230 | 1,073,741,824 |
| Tera | T | 2 40 2^{40} 240 | 1,099,511,627,776 |
| Peta | P | 2 50 2^{50} 250 | 1,125,899,906,842,624 |
| Exa | E | 2 60 2^{60} 260 | 1,152,921,504,606,846,976 |
| Zetta | Z | 2 70 2^{70} 270 | 1,180,591,620,717,411,303,424 |
| Yotta | Y | 2 80 2^{80} 280 | 1,208,925,819,614,629,174,706,176 |
You can see in this chart that kilo is about a thousand, mega is about a million, giga is about a billion, and so on. So when someone says, “This computer has a 2 gig hard drive,” what he or she means is that the hard drive stores 2 gigabytes, or approximately 2 billion bytes, or exactly 2,147,483,648 bytes. How could you possibly need 2 gigabytes of space? When you consider that one CD holds 650 megabytes, you can see that just three CDs worth of data will fill the whole thing! Terabyte databases are fairly common these days, and there are probably a few petabyte databases floating around the Pentagon by now.
从这个图表中,你可以看出千(kilo)大约是一千,兆(mega)大约是一百万,吉(giga)大约是一十亿,依此类推。所以当有人说:“这台电脑有一个 2 吉的硬盘”时,他的意思是硬盘的存储容量为 2 吉字节,即大约 20 亿字节,或者确切地说是 2,147,483,648 字节。你可能需要 2 吉字节的空间吗?当你考虑到一张 CD 可以容纳 650 兆字节时,你会发现仅仅三张 CD 的数据量就能填满整个硬盘!如今,太字节(terabyte)的数据库已经相当常见了,而且在五角大楼周围可能已经有一些拍字节(petabyte)的数据库在运行了。
Binary math works just like decimal math, except that the value of each bit can be only 0 or 1. To get a feel for binary math, let’s start with decimal addition and see how it works. Assume that we want to add 452 and 751:
二进制数学的运算方式与十进制数学相同,只是每个位的值只能是 0 或 1。为了感受二进制数学的魅力,我们先从十进制加法开始,看看它是如何工作的。假设我们想把 452 和 751 相加:
452
+ 751
---
1203
To add these two numbers together, you start at the right: 2 + 1 = 3. No problem. Next, 5 + 5 = 10, so you save the zero and carry the 1 over to the next place. Next, 4 + 7 + 1 (because of the carry) = 12, so you save the 2 and carry the 1. Finally, 0 + 0 + 1 = 1. So the answer is 1203.
将这两个数字相加时,你从右边开始:2 + 1 = 3。没问题。接下来,5 + 5 = 10,所以你把 0 保留下来,然后把 1 进位到下一个位置。再接下来,4 + 7 + 1(因为进位)= 12,所以你把 2 保留下来,再把 1 进位。最后,0 + 0 + 1 = 1。所以答案是 1203。
Binary addition works exactly the same way:
二进制加法的运算方式完全相同:
010
+ 111
---
1001
Starting at the right, 0 + 1 = 1 for the first digit. No carrying there. You’ve got 1 + 1 = 10 for the second digit, so save the 0 and carry the 1. For the third digit, 0 + 1 + 1 = 10, so save the zero and carry the 1. For the last digit, 0 + 0 + 1 = 1. So the answer is 1001. If you translate everything over to decimal you can see it is correct: 2 + 7 = 9.
从右边开始,第一个数字是 0 + 1 = 1。那里没有进位。第二个数字是 1 + 1 = 10,所以保留 0 并进位 1。第三个数字是 0 + 1 + 1 = 10,所以保留 0 并进位 1。最后一个数字是 0 + 0 + 1 = 1。所以答案是 1001。如果你把所有内容都转换为十进制,你可以看到它是正确的:2 + 7 = 9。
To sum up, here’s what we’ve learned about bits and bytes:
总结一下,我们已经了解了关于位和字节的内容:
-
Bits are binary digits. A bit can hold the value 0 or 1.
位是二进制数字。一个位可以存储 0 或 1 的值。 -
Bytes are made up of 8 bits each.
每个字节由 8 位组成。 -
Binary math works just like decimal math, but each bit can have a value of only 0 or 1.
二进制数学的运算方式与十进制数学相同,只是每个位只能有 0 或 1 的值。
There really is nothing more to it – bits and bytes are that simple.
事实就是如此——位和字节就是这么简单。
How Boolean Logic Works
By Marie Look | Updated: May 22, 2024
Boolean logic affects how computers operate. MONTY RAKUSEN / GETTY IMAGES
布尔逻辑影响计算机的运行方式。MONTY RAKUSEN / GETTY IMAGES
A subsection of mathematical logic, Boolean logic deals with operations involving the two Boolean values: true and false.
作为数理逻辑的一个分支,布尔逻辑处理涉及两个布尔值(真和假)的操作。
Although Boolean logic dates back to the mid-19th century, it became foundational to modern computer programming and data querying through a method called Boolean algebra. Mathematicians, engineers and programmers working on Boolean algebra problems use rules to manipulate these logical values, typically under the binary system of 1 (true) and 0 (false).
尽管布尔逻辑可以追溯到 19 世纪中期,但它通过一种称为布尔代数的方法成为现代计算机编程和数据查询的基础。从事布尔代数问题的数学家、工程师和程序员使用规则来操作这些逻辑值,通常是在 1(真)和 0(假)的二进制系统下进行的。
To better understand the role Boolean logic plays in computing and its other applications, it’s necessary to first learn the basic principles, including Boolean operators and expressions.
为了更好地理解布尔逻辑在计算和其他应用中的作用,首先需要学习基本原理,包括布尔运算符和布尔表达式。
What Is Boolean Logic?
In simple words, Boolean logic refers to a form of algebra where the values of the variables are the truth values (also called Boolean values): “true” and “false,” often denoted as 1 and 0 respectively.
简单来说,布尔逻辑是一种代数形式,其中变量的值是真值(也称为布尔值):“真”和“假”,通常分别表示为 1 和 0。
The term “Boolean” comes from the 19th-century English mathematician George Boole, who was the first person to define an algebraic framework for working with logical operations.
“布尔”一词来源于 19 世纪英国数学家乔治·布尔,他是第一个定义用于逻辑运算的代数框架的人。
Computing sometimes represents the Boolean values as “high” and “low” voltage levels, such as five volts for true and zero volts for false.
在计算机中,布尔值有时被表示为“高”和“低”电压水平,例如,真值用 5 伏特表示,假值用 0 伏特表示。
Basic Boolean Operators
布尔逻辑需要所谓的运算符来对布尔值(真和假)执行逻辑运算。你可能还会看到人们或程序将布尔运算符称为布尔门或逻辑门。
布尔逻辑需要所谓的运算符来对布尔值(真和假)执行逻辑运算。你可能还会看到人们或程序将布尔运算符称为布尔门或逻辑门。
There are three basic Boolean operators:
布尔逻辑中有三种基本的布尔运算符:
-
AND (conjunction): This operator returns true if both of its arguments are true. For example, the expression “true AND true” will return true.
-
OR (disjunction): This operator returns true if at least one of the arguments is true. For example, the expression “true OR false” will also return true.
-
NOT (negation): This operator takes one argument and inverts it, returning true if the input is false and vice versa. For instance, if “x” is a Boolean variable holding the value true, then “NOT x” would equate to false.
-
AND(与,合取):如果它的两个参数都为真,这个运算符返回真。例如,表达式“真 AND 真”将返回真。
-
OR(或,析取):如果至少有一个参数为真,这个运算符返回真。例如,表达式“真 OR 假”也将返回真。
-
NOT(非,否定):这个运算符接收一个参数并将其反转,如果输入为假则返回真,反之亦然。例如,如果“x”是一个布尔变量,其值为真,那么“NOT x”将等于假。
Boolean Expressions
A Boolean expression is a combination of Boolean values and operators that yields another Boolean value. To evaluate these expressions you have to use Boolean algebra, which has rules for how to deal with Boolean values and operators.
布尔表达式是布尔值和布尔运算符的组合,它产生另一个布尔值。要计算这些表达式,你需要使用布尔代数,它有一套处理布尔值和布尔运算符的规则。
Boolean expressions are fundamental to programming languages and database queries. In computer programs, they help determine the flow of execution through specific conditions.
布尔表达式是编程语言和数据库查询的基础。在计算机程序中,它们有助于通过特定条件确定执行流程。
In database queries, Boolean expressions define specific search criteria in the databases. For example, a search statement in a database might use a Boolean expression to filter records according to certain dates or names.
在数据库查询中,布尔表达式定义了数据库中的特定搜索标准。例如,数据库中的一个搜索语句可能会使用布尔表达式根据特定日期或名称过滤记录。
Nesting
It’s possible to combine multiple Boolean operators in a Boolean expression. When this occurs, it’s called nesting, and it often requires the use of parentheses for clarity. For instance, “(true AND false) OR true” is a Boolean expression.
可以在布尔表达式中组合多个布尔运算符。当这种情况发生时,它被称为嵌套,并且通常需要使用括号来清晰表达。例如,“(真 AND 假) OR 真”是一个布尔表达式。
Venn Diagrams and Truth Tables
To visually represent the results of Boolean operations, it’s common to use Venn diagrams and truth tables. A Venn diagram shows all possible logical relations between a finite collection of different sets. It can visually simplify for you the possible outcomes of various Boolean operations.
为了直观地表示布尔运算的结果,通常使用维恩图和真值表。维恩图显示了不同集合之间所有可能的逻辑关系。它可以直观地简化各种布尔运算的可能结果。
On the other hand, a truth table is a table that lists all possible combinations of inputs for Boolean operators and the resultant output.
另一方面,真值表是一个表格,它列出了布尔运算符的所有可能输入组合及其结果输出。
For example, a truth table for the AND operator with two inputs would look like this:
例如,具有两个输入的 AND 运算符的真值表如下所示:
| A | B | A AND B |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
The above truth table demonstrates how the AND operator requires all given conditions (inputs) to be true to produce a true outcome.
上述真值表展示了 AND 运算符如何要求所有给定条件(输入)都为真,才能产生真结果。
The AND gate can be particularly useful in situations where multiple criteria need to be satisfied simultaneously, such as in security systems where multiple conditions must be met to grant access, or in programming where several conditions must be true to execute a block of code.
AND 门在需要同时满足多个标准的情况下特别有用,例如在安全系统中,必须满足多个条件才能授予访问权限,或者在编程中,必须满足几个条件才能执行代码块。
Flip-flops
It’s possible to create computer memory with Boolean gates using special circuits called flip-flops and a concept known as feedback.
可以使用称为触发器的特殊电路和一种称为反馈的概念,通过布尔门创建计算机内存。
The flip-flop circuits are made up of several logic gates linked together in a way that allows them to hold onto a binary state (0 or 1, representing false or true). Essentially, these circuits use feedback loops where the output of certain gates is looped back as an input. This allows the flip-flop to maintain its state (store a 1 or a 0) until it receives a signal to change.
触发器电路由多个逻辑门连接而成,它们可以保持一个二进制状态(0 或 1,分别表示假或真)。本质上,这些电路使用反馈环路,将某些门的输出作为输入回环。这使得触发器可以保持其状态(存储 1 或 0),直到它收到改变的信号。
Basic memory cells in computers can store information this way. Each flip-flop holds one bit of data, acting as a tiny memory unit. By stringing together thousands to millions of these, you can build up the memory systems used in devices like smartphones and computers, where they store everything from user settings to the current state of apps.
计算机的基本存储单元可以以这种方式存储信息。每个触发器存储一位数据,作为一个微小的存储单元。通过将数千到数百万个这样的单元串联起来,你可以构建出用于智能手机和计算机等设备的存储系统,它们存储从用户设置到应用程序当前状态的所有内容。
This simple concept forms the basis for random-access memory (RAM.), a type of computer memory that can be accessed randomly at any time, allowing data to be read and written quickly no matter where the data is located physically inside the memory.
这个简单的概念构成了随机存取存储器(RAM)的基础,这是一种可以在任何时间随机访问的计算机存储器,允许快速读写数据,无论数据在存储器中的物理位置如何。
Applications of Boolean Logic
布尔值因其简单性,在各种技术和应用中发挥着关键作用,能够实现决策过程、控制操作并高效地筛选数据。
布尔值因其简单性,在各种技术和应用中发挥着关键作用,能够实现决策过程、控制操作并高效地筛选数据。
Computer Programming
布尔逻辑是开发算法和在编程语言中实现控制流的核心。布尔逻辑运算使程序员能够在代码中实现决策过程,通过评估返回真或假的条件。
布尔逻辑是开发算法和在编程语言中实现控制流的核心。布尔逻辑运算使程序员能够在代码中实现决策过程,通过评估返回真或假的条件。
For example, Boolean expressions are crucial in “if” statements and “while” loops and for validating conditions during software operations. These expressions determine which blocks of code are executed based on the outcomes of the Boolean evaluations.
例如,布尔表达式在“if”语句和“while”循环中至关重要,并且在软件操作期间验证条件。这些表达式根据布尔评估的结果决定执行哪些代码块。
In a programming language like Python, Boolean values often have use in control structures, such as:
在像 Python 这样的编程语言中,布尔值通常用于控制结构,例如:
if is_logged_in: # is_logged_in is a Boolean variable that can be either true or false
print("Access granted.")
else:
print("Access denied.")
如果用户已登录(is_logged_in 为真),则授予访问权限;否则拒绝访问。
Digital Electronics
Boolean logic is fundamental in digital electronics, where it governs how different logic gates process binary signals to perform calculations and make decisions.
布尔逻辑是数字电子学的基础,它决定了不同的逻辑门如何处理二进制信号以执行计算和做出决策。
These gates are the building blocks for complex digital circuits, including multiplexers, demultiplexers and arithmetic logic units — all of which are essential for carrying out operations in microprocessors and other electronic devices.
这些门是复杂数字电路的构建块,包括多路复用器、多路解复用器和算术逻辑单元 —— 所有这些对于在微处理器和其他电子设备中执行操作都是必不可少的。
In these types of circuits, Boolean values determine the output (voltage) based on the inputs. For example, in an OR gate, the output is true if any of the inputs are true. Here, true could be represented by a high voltage, and false by zero volts.
在这些类型的电路中,布尔值根据输入决定输出(电压)。例如,在 OR 门中,如果任何一个输入为真,则输出为真。在这里,真可以用高电压表示,假用零伏特表示。
Additionally, Boolean logic is instrumental in designing and analyzing the behavior of circuits in both small-scale integrated circuits (ICs) and large-scale systems, ensuring they operate correctly according to the logical rules the programmer has specified.
此外,布尔逻辑在设计和分析小规模集成电路(IC)和大规模系统中的电路行为方面起着关键作用,确保它们根据程序员指定的逻辑规则正确运行。
Database Queries and Search Engines
In databases and search engines, Boolean logic allows users to filter and retrieve data based on specific criteria. This helps them create more focused queries, especially when searching through large datasets.
在数据库和搜索引擎中,布尔逻辑允许用户根据特定标准筛选和检索数据。这有助于他们在搜索大型数据集时创建更精确的查询。
By employing Boolean operators like AND, OR and NOT, users can specify whether they want to include multiple terms together, at least one of several terms or exclude certain terms from their search results. This enables the search engine to better understand the intent behind the user’s query and to filter and prioritize content that best matches the user’s search criteria.
通过使用 AND、OR 和 NOT 等布尔运算符,用户可以指定他们是否希望在搜索结果中包含多个术语、至少几个术语中的一个,或者排除某些术语。这使得搜索引擎能够更好地理解用户查询的意图,并筛选和优先显示最符合用户搜索标准的内容。
For example:
例如:
-
Searching for “apple AND juice” will return results that include both terms.
搜索“apple AND juice”将返回包含这两个术语的结果。 -
Searching for “apple OR orange” gives results that include either term.
搜索“apple OR orange”将返回包含这两个术语中至少一个的结果。 -
Using “apple NOT pie” provides results that include “apple” but exclude “pie.”
使用“apple NOT pie”将返回包含“apple”但不包含“pie”的结果。
Conditional Formulas
In spreadsheet applications, Boolean logic is used extensively within conditional formulas to make decisions based on specific criteria. For example, using the IF function, a user can create a formula that checks whether a condition is true or false and then performs different actions based on the result:
在电子表格应用程序中,布尔逻辑广泛用于条件公式中,根据特定标准进行决策。例如,使用 IF 函数,用户可以创建一个公式,检查某个条件是否为真或假,然后根据结果执行不同的操作。
=IF(A1 > 10, TRUE, FALSE)
The above formula checks if the value in cell A1 is greater than 10. If it is, the formula returns true; otherwise, it returns false.
上述公式检查单元格 A1 中的值是否大于 10。如果是,则公式返回真;否则返回假。
This application of Boolean logic allows the spreadsheet user to automate certain data management tasks, helping them to organize, analyze and visualize the data efficiently based on logical conditions.
这种布尔逻辑的应用使电子表格用户能够自动化某些数据管理任务,帮助他们根据逻辑条件高效地组织、分析和可视化数据。
Boolean Algebra Basics—An Overview of Boolean Logic
布尔代数基础 — 布尔逻辑概览
July 28, 2022 by William Bahn
New to digital logic, want a refresher, or to dive deeper into Boolean algebra? This article teaches the basics of Boolean algebra and prepares you for further learning.
是数字逻辑的新手,需要复习,还是想深入学习布尔代数?本文介绍了布尔代数的基础知识,为你进一步学习做好准备。
For those with little or no exposure to digital logic and those wanting a refresher or to understand Boolean algebra at a deeper level, this article walks through the basics of Boolean algebra. The goal is to prepare you for subsequent articles that delve deeper into aspects of Boolean algebra.
对于那些对 数字逻辑 知之甚少甚至一无所知的人,以及那些希望复习或更深入理解 布尔代数 的人,本文将逐步介绍布尔代数的基础知识。目标是为你后续深入学习布尔代数的各个方面做好准备。
Boolean Logic or Digital Logic—What is Boolean Algebra?
布尔逻辑还是数字逻辑 — 布尔代数是什么?
Our focus is more geared toward engineers and technicians and not toward mathematicians and philosophers; thus, we describe Boolean algebra as the manipulation of two-state signals to implement logic functions. At its core is a deceptively simple set of concepts, namely signals, that can take on only one of two values (states) at any moment, combined with three fundamental operations that the user can apply to those signals.
我们的关注点更多地偏向工程师和技术人员,而不是数学家和哲学家;因此,我们将布尔代数描述为通过操作双态信号来实现逻辑功能。其核心是一组看似简单但实则复杂的概念,即信号在任何时刻只能取两个值(状态)中的一个,并且用户可以对这些信号应用三种基本操作。
For most engineers and technicians, the terms “digital logic” and “Boolean logic” are synonymous. In contrast, “Boolean algebra” is slightly different, implying a more math-oriented approach to analyzing or designing digital systems.
对于大多数工程师和技术人员来说,“数字逻辑”和“布尔逻辑”是同义词。相比之下,“布尔代数”略有不同,它暗示了一种更偏向数学的方法来分析或设计数字系统。
Boolean algebra (named in honor of George Boole) involves only two values—FALSE and TRUE. Sometimes we use different names depending on what makes sense; common names are {F, T}, {LO, HI}, {L, H}, or {0, 1}.
布尔代数(以 乔治·布尔 的名字命名)只涉及两个值 — FALSE 和 TRUE。有时我们会根据实际情况使用不同的名称;常见的名称有 {F, T}、{LO, HI}、{L, H} 或 {0, 1}。
Like normal algebra, we have Boolean operators that take one or two operands and produce a value (a Boolean value). An “operand” is nothing more than a value (or signal), and an “operator” is nothing more than some manipulation of the values to produce a result. In normal arithmetic, the expression “2 + 3” has two operands (the “2” and the “3”) and one operator (the “+”), which produce the result “5”.
和普通代数一样,布尔运算符接受一个或两个操作数并产生一个值(布尔值)。一个“操作数”不过是一个值(或信号),而一个“运算符”不过是对值进行操作以产生结果。在普通算术中,表达式 “2 + 3” 有两个操作数(“2” 和 “3”)和一个运算符(“+”),产生结果 “5”。
Boolean algebra involves three primitive operators, one unary (takes one operand) and two binary (takes two operands)—the unary operator is the logical negation (NOT) operator. On the other hand, the binary operators are the logical disjunction (OR) and logical conjunction (AND). That’s all there is to keep track of: two possible values, FALSE and TRUE, manipulated by three operators, NOT, OR, and AND_。
布尔代数涉及三种基本运算符,一种一元运算符(接受一个操作数)和两种二元运算符(接受两个操作数) — 一元运算符是逻辑非(NOT)运算符。另一方面,二元运算符是逻辑或(OR)和逻辑与(AND)。这就是需要记住的全部内容:两个可能的值,FALSE 和 TRUE,由三种运算符 NOT、OR 和 AND 操作。
Now is a good time to point out that different terminology is used in different fields. We speak about logic operators and logic functions in more math-centric fields, while in more engineering-centric fields, we talk about logic gates. However, in each case, we are taking one or more input signals (operands) and using a logic gate (logic operator) to produce an output signal (result) that depends only on the current input signals.
现在指出不同领域使用不同的术语是很好的时机。在更偏向数学的领域,我们谈论逻辑运算符和逻辑函数,而在更偏向工程的领域,我们谈论 逻辑门。然而,在每种情况下,我们都是在取一个或多个输入信号(操作数),并使用逻辑门(逻辑运算符)产生一个仅取决于当前输入信号的输出信号(结果)。
As a quick note, for those who already know about combinational logic and sequential logic, we will keep the discussion focused on combinatorial logic—for those who don’t know about these two types of logic, you can ignore this note.
作为一个快速说明,对于那些已经了解 组合逻辑 和时序逻辑的人,我们将讨论重点放在组合逻辑上 — 对于那些不了解这两种逻辑的人,可以忽略这个注释。
Since AAC is very engineering-centered, we will use the terminology most commonly found in engineering fields. However, as we introduce the basic gates in the next section, we will present the operator notation used in engineering and math. This approach can be useful because most engineers and technicians will have discussions from time to time with people that use non-engineering notation.
由于 AAC 非常注重工程,我们将使用工程领域中最常见的术语。然而,在下一部分介绍基本门时,我们将介绍工程和数学中使用的运算符符号。这种方法很有用,因为大多数工程师和技术人员会不时与使用非工程符号的人进行讨论。
Boolean Truth Table
布尔真值表
Since Boolean algebra is so constrained as to the values the signals can take, we can describe or even define functions by exhaustively listing all possible combinations of the input signals along with the value of the resulting output. This list is known as a truth table。
由于布尔代数对信号可以取的值限制得很严格,我们可以通过列出所有可能的输入信号组合以及结果输出的值来描述甚至定义函数。这个列表被称为 真值表。
An example truth table can be seen in Table 1.
表 1 中可以看到一个示例真值表。
Table 1. An example truth table.
表 1. 示例真值表
| A | B | Y |
|---|---|---|
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
In this table, ‘A’ and ‘B’ are the input signals, and ‘Y’ is the output signal. The usual convention is that inputs are listed in the left-hand columns and outputs in the right-hand columns. If there are any, intermediate signals go between the input and output columns. Since we will only discuss gates with a single output and no intermediate signals, the right-most column is the output, and all other columns are inputs.
在这个表中,“A”和“B”是输入信号,“Y”是输出信号。通常的惯例是输入信号列在左侧的列中,输出信号列在右侧的列中。如果有中间信号,则它们会出现在输入和输出列之间。由于我们只讨论具有单个输出且没有中间信号的门,因此最右边的列是输出,其他所有列都是输入。
This example table is sufficient to define a particular Boolean gate. If we were to describe this gate in words, we might say something like, “The output is TRUE if and only if both inputs are the same.” We might then give this gate the name “Equality Gate” with the symbol “EQ” and write expressions as:
这个示例表足以定义一个特定的布尔门。如果我们用文字描述这个门,我们可能会说:“当且仅当两个输入相同时,输出为 TRUE。”然后我们可能会给这个门命名为“等值门”,符号为“EQ”,并写出如下表达式:
Y = A E Q B Y = A \ EQ \ B Y=A EQ B
From there we can say that Y is TRUE if and only if A equals B.
从这里我们可以得出结论:当且仅当 A 等于 B 时,Y 为 TRUE。
Concerning simple gates (and even moderately complex logic functions), truth tables are the preferred way of describing and defining them because they are unambiguous.
对于简单的门(甚至中等复杂程度的逻辑函数),真值表是描述和定义它们的首选方法,因为它们是明确无误的。
For instance, what if we just said that we wanted a gate whose output was TRUE if the two inputs were equal? This situation is ambiguous because we haven’t actually said what the output should be when they aren’t equal. Similarly, if we say that we want a gate whose output is TRUE only when the outputs are equal, we haven’t actually said what the output should be when they ARE equal. We’ve only ruled out what they can be equal to when they aren’t equal.
例如,如果我们只是说我们想要一个当两个输入相等时输出为 TRUE 的门呢?这种情况是模糊的,因为我们实际上并没有说当它们不相等时输出应该是什么。同样,如果我们说我们想要一个只有当输出相等时输出才为 TRUE 的门,我们实际上并没有说当它们相等时输出应该是什么。我们只是排除了它们在不相等时可以相等的情况。
We could certainly argue that in both of these cases, “it’s obvious”—and, in these simple cases, it would be a very strong argument. However, in general, it may not be obvious, and we end up relying on the person reading the description to interpret it the way we did when we wrote it. This situation can be a recipe for miscommunication and potential disaster.
我们当然可以争辩说,在这两种情况下,“这是显而易见的” —— 而且,在这些简单的情况下,这将是一个非常有力的论点。然而,一般来说,这可能并不明显,我们最终依赖于阅读描述的人以我们写描述时的方式去理解它。这种情况可能会导致误解和潜在的灾难。
A truth table leaves little to no room for misinterpretation (provided that we use a “proper” truth table, meaning that all possible input combinations are included).
一个真值表几乎没有留下任何误解的空间(前提是使用一个“正确的”真值表,即包含所有可能的输入组合)。
Condensed Truth Tables
简化真值表
Table 1 above has exactly one row for each possible combination of inputs and is therefore known as an “explicit” or a “fully-enumerated” truth table. But the number of rows needed for such a table grows exponentially with the number of inputs.
表 1 上面的表为每种可能的输入组合都恰好有一行,因此被称为“明确的”或“完全枚举的”真值表。但是,这种表所需的行数会随着输入数量的增加而呈指数增长。
For instance, a device with just six inputs would require sixty-four rows. Not only would this take up a lot of space, but it makes the truth table much more difficult to comprehend for most humans. So we devise shortcuts to enable us to describe multiple rows from the explicit table in a single row of what is known as a “condensed” truth table. Several conventions are used, but here we will only use one: the “don’t care.”
例如,一个只有六个输入的设备就需要 64 行。这不仅会占用大量空间,而且对于大多数人来说,会使真值表更难理解。因此,我们设计了一些捷径,使我们能够在所谓的“简化”真值表的一行中描述明确表的多行。虽然有几种约定,但在这里我们只使用一种:“无关”。
Consider the following table in Table 2.
考虑表 2 中的以下表。
Table 2. An example condensed truth table.
表 2. 示例简化真值表。
| A | B | Y |
|---|---|---|
| 0 | X | 0 |
| X | 0 | 0 |
| 1 | 1 | 1 |
The ‘X’ in a given cell means that that row applies for ANY value of that input. So the first row of the above table says that if A is 0, the output is 0 regardless of what value B might have. Similarly, it says that if B is 0, the output is 0, regardless of what value A might have.
在给定单元格中的“X”意味着这一行适用于该输入的任何值。因此,上面表中的第一行表示,如果 A 为 0,则无论 B 可能是什么值,输出都为 0。同样,它表示如果 B 为 0,则无论 A 可能是什么值,输出都为 0。
One potential problem with a condensed truth table is when multiple rows apply to the same set of input values. For instance, which row governs the behavior when both A and B are 0?
简化真值表的一个潜在问题是,当多行适用于同一组输入值时。例如,当 A 和 B 都为 0 时,哪一行决定了行为?
Since both the first and second rows apply, the table is “over-defined.” However, as long as all rows that apply to a given set of inputs produce the same output, the table is consistent and still valid. If they are inconsistent, then the table is not an accurate truth table.
由于第一行和第二行都适用,因此该表是“过度定义的”。然而,只要所有适用于给定输入集的行产生相同的输出,该表就具有一致性,仍然是有效的。如果它们不一致,那么该表就不是一个准确的真值表。
Note that a fully-enumerated truth table can never be invalid—it might be “wrong,” meaning that it doesn’t represent the logic function we wanted. Still, it will always represent a valid Boolean function.
请注意,一个完全枚举的真值表永远不会无效 —— 它可能是“错误的”,即它没有表示我们想要的逻辑函数,但它总是会表示一个有效的布尔函数。
The Three Fundamental Boolean Operators
三种基本布尔运算符
Each of the three fundamental Boolean operators, NOT, OR, and AND, has a schematic symbol used for them (there’s more than one, but the ones we show here are by far the most common) and a truth table that defines them.
三种基本布尔运算符 NOT、OR 和 AND 都有用于它们的示意图符号(不止一种,但我们在这里展示的无疑是最常见的),以及定义它们的真值表。
This section will provide these plus the more common notations used to express them in engineering, programming, and math/logic contexts. Keep in mind that the syntax used by a particular programming language is specified by that language and may be completely different than what is shown here, which is the dominant notation in the C-based languages. Also, programming languages deal with variables that can take on more than just two values, so many have multiple operators that deal with this situation in different ways.
本节将提供这些内容,以及在工程、编程和数学/逻辑环境中表达它们的更常见符号。请记住,特定编程语言所使用的语法由该语言指定,可能与这里展示的完全不同,而这里展示的是 C 语言系中最主要的符号。此外,编程语言处理的变量可以取多于两个值,因此许多语言有多种运算符以不同方式处理这种情况。
As this is well beyond the scope of this treatment, we will not distinguish between these various methods. So, remember that while the programming operators given represent the same logical operation, they are NOT equivalent in the details of how that operation is applied.
由于这远远超出了本文的范围,我们将不会区分这些不同的方法。因此,请记住,尽管给出的编程运算符代表相同的逻辑运算,但在运算的细节上它们并不等价。
The NOT Gate (Logical Negation)
非门(逻辑非)
To get started, Figure 1 shows the symbol for a NOT gate.
首先,图 1 显示了一个非门的符号。

Figure 1. The symbol for the NOT gate
图 1. 非门的符号*
Next, in Table 3, you’ll see a truth table for the NOT gate.
接下来,在表 3 中,你会看到一个非门的真值表。
Table 3. NOT gate truth table.
表 3. 非门真值表*
| A | Y |
|---|---|
| F | T |
| T | F |
| 工程领域 | Y = A ‾ = A ′ = N O T ( A ) = N O T A = − A Y = \overline{A} = A' = NOT(A) = NOTA = -A Y=A=A′=NOT(A)=NOTA=−A |
|---|---|
| 编程领域 | Y = ! A = ∼ A Y = !A = \sim A Y=!A=∼A |
| 数学和形式逻辑 | Y = ¬ A Y = \neg A Y=¬A |
Also known as logical negation, this unary operator merely produces the opposite value of the operand. In common English, we might say, "Y is true if A is NOT true.
也被称为逻辑非,这个一元运算符只是产生操作数的相反值。用普通英语来说,我们可能会说:“如果 A 不为真,那么 Y 为真。”
Notice that, particularly in engineering contexts, we can specify logical negation in multiple ways. In engineering, the three most common ways are with:
请注意,在工程领域,我们可以用多种方式指定逻辑非。在工程领域,最常见的三种方式是:
-
An overbar
一个横线
-
An apostrophe after the operand (known as a “postfix operator”)
操作数后的一个撇号(称为“后缀运算符”)
-
A function-like syntax
一个类似函数的语法
With the function-like syntax, the name might be NOT(), INV(), or NEG() for “not,” “inverse,” or “negation,” respectively. You may also see a negative sign used before the operand (known as a “prefix operator”); however, this is becoming increasingly uncommon.
使用类似函数的语法时,名称可能是 NOT()、INV() 或 NEG(),分别表示“非”、“反向”或“否定”。你也可以看到在操作数前使用负号(称为“前缀运算符”),但这种情况越来越少见。
Additionally, the overbar is easy to write manually, but it is difficult to type into a text document or a computer program; thus, the postfix apostrophe is widely used.
此外,横线手工书写很容易,但很难输入到文本文件或计算机程序中;因此,后缀撇号被广泛使用。
The OR Gate (Logical Disjunction)
或门(逻辑或)
Next, we’ll take a look at the OR gate. Figure 2 shows the symbol for an OR gate.
接下来,我们来看看或门。图 2 显示了一个或门的符号。

Figure 2. OR gate symbol.
图 2. 或门符号。
Table 5 below shows the truth table for the OR gate.
表 5 下面显示了或门的真值表。
Table 5. OR gate truth table.
表 5. 或门真值表。
| A | B | Y |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
| 工程领域 | Y = A + B = O R ( A , B ) = A O R B Y = A + B = OR(A,B) = AORB Y=A+B=OR(A,B)=AORB |
|---|---|
| 编程领域 | Y = A ∣ B = A ∣ ∣ B Y = A | B = A || B Y=A∣B=A∣∣B |
| 数学和形式逻辑 | Y = A ∨ B Y = A \lor B Y=A∨B |
Also known as logical disjunction, this binary operator produces a TRUE output if either of its operands is TRUE. Put another way; it produces a FALSE output if and only if both of its operands are FALSE. In common English, we might say, “Y is true if A is true OR B is true.”
也被称为逻辑或,这个二元运算符如果它的任意一个操作数为 TRUE,则产生一个 TRUE 输出。换句话说,只有当它的两个操作数都为 FALSE 时,它才产生一个 FALSE 输出。用普通英语来说,我们可能会说:“如果 A 为真或 B 为真,则 Y 为真。”
When we speak of signals that are OR-ed together, we often talk about the result being the “sum” of those signals. This usage stems from using the ‘+’ symbol for the OR operator. This terminology is widely and formally accepted. However, it is generally considered poor form to say that we are “adding” these signals together, though you will hear it from time to time.
当我们谈论通过 OR 运算组合在一起的信号时,我们通常会说结果是这些信号的“和”。这种用法源于使用 ‘+’ 符号作为 OR 运算符。这种术语被广泛且正式地接受。然而,通常认为说我们在“相加”这些信号是不恰当的,尽管你有时会听到这种说法。
The AND Gate (Logical Conjunction)
与门(逻辑与)
The final gate we will look at in this article is the AND gate. Figure 3 shows the symbol for the AND gate.
本文最后将介绍与门。图 3 显示了与门的符号。
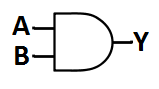
Figure 3. The symbol for the AND gate.
图 3. 与门的符号。
Next, Table 7 will show the truth table for an AND gate.
接下来,表 7 将显示与门的真值表。
Table 7. AND gate truth table.
表 7. 与门真值表。
| A | B | Y |
|---|---|---|
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
Lastly, Table 8 goes over some common ways of expressing AND.
最后,表 8 介绍了一些表达与运算的常见方式。
| 工程领域 | Y = A ⋅ B = A B = ( A ) ( B ) = A N D ( A , B ) = A A N D B Y = A \cdot B = AB = (A)(B) = AND(A,B) = AANDB Y=A⋅B=AB=(A)(B)=AND(A,B)=AANDB |
|---|---|
| 编程领域 | Y = A & B = A & & B Y = A \& B = A \&\& B Y=A&B=A&&B |
| 数学和形式逻辑 | Y = A ∧ B Y = A \land B Y=A∧B |
Also known as logical conjunction, this binary operator produces a TRUE output if and only if BOTH of its operands are TRUE or, put another way, it produces a FALSE output if either of its operands is FALSE. In common English, we might say, “Y is true if A is true AND B is true.”
也被称为逻辑与,这个二元运算符只有当它的两个操作数都为 TRUE 时才产生一个 TRUE 输出,换句话说,如果它的任意一个操作数为 FALSE,则产生一个 FALSE 输出。用普通英语来说,我们可能会说:“如果 A 为真且 B 为真,则 Y 为真。”
When we speak of signals that are AND-ed together, we often talk about the result being the “product” of those signals. This usage stems from the various notations for multiplication used for the AND operator. This terminology is widely and formally accepted. However, it is generally considered poor form to say that we are “multiplying” these signals together, though you will hear it once in a while.
当我们谈论通过 AND 运算组合在一起的信号时,我们通常会说结果是这些信号的“乘积”。这种用法源于用于 AND 运算符的各种乘法符号。这种术语被广泛且正式地接受。然而,通常认为说我们在“相乘”这些信号是不恰当的,尽管你偶尔会听到这种说法。
What About XOR and Others?
那么异或和其他运算符呢?
Some may wonder why XOR (i.e., exclusive-OR) hasn’t yet been mentioned. The reason is that XOR is not a primitive operator in Boolean algebra but rather a composite operator since it can be defined in terms of the primitives already given. Still, it—and a few other composite operators—are worthy of some attention.
有些人可能会好奇,为什么异或(即 XOR)还没有被提及。原因在于 XOR 不是布尔代数中的基本运算符,而是一个复合运算符,因为它可以用已经给出的基本运算符来定义。尽管如此,它以及一些其他复合运算符还是值得关注的。
The symbol for XOR is shown in Figure 4, while the defining truth table is presented in Table 9.
图 4 显示了 XOR 的符号,而定义其的真值表在表 9 中给出。

Figure 4. The symbol for the XOR gate.
图 4. 异或门的符号。
Table 9. XOR truth table.
表 9. 异或真值表。
| A | B | Y |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | F |
Some of the common ways of expressing it are shown in Table 10.
表 10 中展示了一些表达异或的常见方式。
| 工程领域 | Y = X O R ( A , B ) = A ⊕ B Y = XOR(A,B) = A \oplus B Y=XOR(A,B)=A⊕B |
|---|---|
| 编程领域 | Y = A ⊕ B Y = A \oplus B Y=A⊕B |
| 数学和形式逻辑 | Y = A ⊕ B Y = A \oplus B Y=A⊕B |
It is readily verified that the XOR truth table is produced by the following equation given in terms of the primitive operations, thus establishing it as a composite operator.
很容易验证,以下用基本运算表示的方程可以产生 XOR 的真值表,从而证明它是一个复合运算符。
Y = A ⊕ B = A ‾ B + A B ‾ Y = A \oplus B = \overline{A}B + A\overline{B} Y=A⊕B=AB+AB
There are three other common composite operators: XNOR, NAND, and NOR, whose symbols and truth tables are shown in Figure 5.
还有三个其他常见的复合运算符:XNOR、NAND 和 NOR,它们的符号和真值表在图 5 中显示。

Figure 5. Additional common composite operators.
图 5. 其他常见复合运算符。
The equations that produce these truth tables, in terms of the primitive operations, are shown in Figure 6. [img](https://i-blog.csdnimg.cn/direct/04bdf37913eb411cbbb22eb0a4403b49.png =300x)
图 6 中展示了用基本运算表示的产生这些真值表的方程。
| 逻辑运算 | 表达式 |
|---|---|
| 异或(XOR) | Y = XOR ( A , B ) = A ⊕ B = A ‾ B + A B ‾ Y = \text{XOR}(A, B)=A \oplus B=\overline{A}B + A\overline{B} Y=XOR(A,B)=A⊕B=AB+AB |
| 同或(XNOR) | Y = XNOR ( A , B ) = A ⊙ B = A B + A ‾ B ‾ Y = \text{XNOR}(A, B)=A \odot B = AB+\overline{A}\overline{B} Y=XNOR(A,B)=A⊙B=AB+AB |
| 与非(NAND) | Y = NAND ( A , B ) = A B ‾ Y = \text{NAND}(A, B)=\overline{AB} Y=NAND(A,B)=AB |
| 或非(NOR) | Y = NOR ( A , B ) = A + B ‾ Y = \text{NOR}(A, B)=\overline{A + B} Y=NOR(A,B)=A+B |
Figure 6. Primitive expressions for the common composite operators.
图 6. 常见复合运算符的基本表达式。
XOR is a sufficiently common operation for which the operator symbol has gained wide acceptance and is commonly seen in Boolean equations. This, however, does not make it a primitive operator. The other gates also have operator symbols; however, the one for XNOR is rarely seen while the ones for the other operations are seldom seen outside of formal logic proofs.
XOR 是一种足够常见的运算,其运算符符号已被广泛接受,并且在布尔方程中常见。然而,这并不使它成为一个基本运算符。其他门也有运算符符号;然而,XNOR 的运算符符号很少见,而其他运算的运算符符号除了在形式逻辑证明中很少见到。
Operator Precedence and Associativity
运算符优先级和结合性
Operator precedences (also known as the order of operations) are rules that dictate which operator is executed first when we would otherwise have the choice of picking between two different operators (or, more correctly, two operators of different precedence).
运算符优先级(也称为运算顺序)是规定在我们本可以选择两个不同运算符(或者更准确地说,两个优先级不同的运算符)时,哪一个运算符先被执行的规则。
Operator associativity, on the other hand, is simply a rule that dictates which operator is executed first when we would otherwise have the choice of picking between two operators that are the same (or, more correctly, two operators of the same precedence).
另一方面,运算符结合性仅仅是规定在我们本可以选择两个相同运算符(或者更准确地说,两个优先级相同的运算符)时,哪一个运算符先被执行的规则。
Since a given Boolean expression, if evaluated according to the precedence and associativity rules, might not implement the desired logic function, we can override those rules using parentheses. Strictly speaking, these parentheses are simply another operator with the highest precedence.
由于根据优先级和结合性规则评估的一个给定的布尔表达式可能无法实现所需的逻辑功能,因此我们可以使用括号来覆盖这些规则。严格来说,这些括号只是另一个具有最高优先级的运算符。
Before discussing precedence and associativity rules for Boolean algebra, let’s examine them for the normal algebra and arithmetic we are comfortable using. In the absence of parentheses, we know that multiplication and division have precedence over addition and subtraction. This situation is why multiplication and division are said to have “higher precedence” or be “higher order” than addition or subtraction. We also know that if we have multiple multiplication and/or division operators, we execute them left to right; the same goes for multiple addition and/or subtraction operators. This is known as “left associativity.”
在讨论布尔代数的优先级和结合性规则之前,让我们先来研究我们熟悉的普通代数和算术中的这些规则。在没有括号的情况下,我们知道乘法和除法的优先级高于加法和减法。这就是为什么说乘法和除法的“优先级更高”或“顺序更高”于加法或减法。我们还知道,如果有多个乘法和/或除法运算符,我们将从左到右执行它们;对于多个加法和/或减法运算符也是如此。这被称为“左结合性”。
Let’s examine how these rules are applied to the following expression.
让我们来研究这些规则是如何应用于以下表达式的。
A + B ∗ C / D − E + F ∗ G / H ∗ I − J ∗ K + L A + B \ast C / D - E + F \ast G / H \ast I - J \ast K + L A+B∗C/D−E+F∗G/H∗I−J∗K+L
Since multiplication and division are the highest precedence operators present, we first split the expression into groups that contain only these two operators. We’ll use square brackets for this purpose (we will remove these later).
由于乘法和除法是存在的最高优先级的运算符,我们首先将表达式分成只包含这两个运算符的组。为此,我们将使用方括号(稍后我们会去掉这些方括号)。
A + [ B ∗ C / D ] − E + [ F ∗ G / H ∗ I ] − [ J ∗ K ] + L A + [B \ast C / D] - E + [F \ast G / H \ast I] - [J \ast K] + L A+[B∗C/D]−E+[F∗G/H∗I]−[J∗K]+L
Within each group, “factors” are all operands for a multiplication or division operator. We evaluate these operators according to associativity, which is left-to-right (left associative) for multiplication and division.
在每个组内,“因子”是乘法或除法运算符的所有操作数。我们根据结合性(对于乘法和除法是左到右的,即左结合性)来计算这些运算符。
A + [ ( ( B ∗ C ) / D ) ] − E + [ ( ( ( F ∗ G ) / H ) ∗ I ) ] − [ ( J ∗ K ) ] + L A + [((B \ast C) / D)] - E + [(((F \ast G) / H) \ast I)] - [(J \ast K)] + L A+[((B∗C)/D)]−E+[(((F∗G)/H)∗I)]−[(J∗K)]+L
At this point, we have “terms” that are all operands for an addition or subtraction operator. We could have removed the square brackets at this point, but they are useful in visually identifying terms made up of multiple factors. From here, we can now evaluate the addition and subtraction operators according to their associativity (i.e., left associative in this case). Let’s go ahead and remove the square brackets at this time.
此时,我们得到了“项”,它们是加法或减法运算符的所有操作数。我们本可以在这一点去掉方括号,但它们在视觉上识别由多个因子组成的项方面很有用。从这里开始,我们现在可以根据它们的结合性(即左结合性)来计算加法和减法运算符。让我们现在去掉方括号。
( ( ( ( ( A + ( ( B ∗ C ) / D ) ) − E ) + ( ( ( F ∗ G ) / H ) ∗ I ) ) − ( J ∗ K ) ) + L ) (((((A + ((B \ast C) / D)) - E) + (((F \ast G) / H) \ast I)) - (J \ast K)) + L) (((((A+((B∗C)/D))−E)+(((F∗G)/H)∗I))−(J∗K))+L)
This equation is known as a “fully-parenthesized” expression whose significance is that it is independent of the precedence and associativity rules. The reason is simple, those rules dictate which operator to evaluate when we have a choice, but a fully-parenthesized expression gives us no such choices.
这个方程被称为“完全括号化”的表达式,其重要意义在于它独立于优先级和结合性规则。原因很简单,这些规则规定了在我们有选择时要计算哪一个运算符,但一个完全括号化的表达式并没有给我们这样的选择。
Shifting our attention to Boolean algebra, we discover that there are no precedence and associativity rules that are universal. This aspect is particularly true when we start adding more operators, which are nothing but shortcut notations for certain combinations of the three fundamental ones.
将注意力转向布尔代数,我们发现并没有普遍适用的优先级和结合性规则。当我们开始添加更多的运算符时,这种情况尤其如此,而这些运算符不过是三种基本运算符的某些组合的简写符号。
Programming languages, by their nature, have well-defined precedence and associativity rules; however, they may vary significantly from one language to another. For this reason, it is best to write Boolean expressions with a liberal dose of parentheses.
编程语言本质上具有明确的优先级和结合性规则,但这些规则可能因语言而异。因此,最好在布尔表达式中大量使用括号。
With that in mind, most programming languages have converged on a fairly consistent convention, which is a reasonably natural, albeit somewhat arbitrary, outgrowth of the operator notation used. In normal arithmetic, the unary minus sign (the negative sign) has higher precedence than either multiplication or addition.
考虑到这一点,大多数编程语言已经形成了一个相当一致的惯例,这是所使用的运算符符号的一个相当自然的、尽管有些武断的延伸。在普通算术中,一元减号(负号)的优先级高于乘法或加法。
Since we use the multiplication symbol for AND and the addition symbol for OR, this leads to the Boolean precedence of NOT, AND, and OR (in order from highest to lowest). As is the case with most binary operators, AND and OR are both left associative. The associativity of NOT depends on the notation used. If a prefix operator is used, such as the ‘~’, the ‘!’, the ‘¬’, or even the non-function-like ‘NOT’, then the operator is right associative. On the other hand, if a postfix operator is used, such as the trailing apostrophe, the operator is left associative.
由于我们使用乘法符号表示 AND,使用加法符号表示 OR,这就导致了布尔优先级为 NOT、AND 和 OR(从高到低)。与大多数二元运算符一样,AND 和 OR 都是左结合的。NOT 的结合性取决于所使用的符号。如果使用前缀运算符,如“~”、“!”、“¬”,甚至是非函数式的“NOT”,那么该运算符是右结合的。另一方面,如果使用后缀运算符,如尾随的撇号,则该运算符是左结合的。
Left Associative NOT:
左结合的 NOT:
NOT NOTA = NOT (NOTA)
∼ ∼ A = ∼ ( ∼ A ) \sim \sim A = \sim (\sim A) ∼∼A=∼(∼A)
If these were left associative, we would have NOT NOT A being the same as (NOT NOT) A, which is nonsensical since an operator operating on an operator is undefined (though, yes, we could define it if we wanted to).
如果这些是左结合的,那么 NOT NOT A 将与 (NOT NOT) A 相同,这是没有意义的,因为一个运算符作用于另一个运算符是未定义的(尽管是的,如果我们愿意,我们可以定义它)。
Right Associative NOT:
右结合的 NOT:
A ′ ′ = ( A ′ ) ′ A'' = (A')' A′′=(A′)′
Similar to the prefix operator, if this postfix operator wasn’t left associative we would have KaTeX parse error: Double superscript at position 4: A' '̲ = A (' ') which would be undefined.
与前缀运算符类似,如果这个后缀运算符不是左结合的,我们将得到 KaTeX parse error: Double superscript at position 4: A' '̲ = A (' '),这是未定义的。
So let’s consider the following example by fully parenthesizing it.
那么让我们通过完全括号化来考虑以下示例。
Y = A A N D N O T B O R N O T A A N D B = A B ′ + A ′ B Y = A \ AND \ NOT \ B \ OR \ NOT \ A \ AND \ B = AB' + A'B Y=A AND NOT B OR NOT A AND B=AB′+A′B
We start with the highest precedence operator, the NOT, and get:
我们从最高优先级的运算符 NOT 开始,得到:
Y = A A N D ( N O T B ) O R ( N O T A ) A N D B = A ( B ′ ) + ( A ′ ) B Y = A \ AND \ (NOT \ B) \ OR \ (NOT \ A) \ AND \ B = A(B') + (A')B Y=A AND (NOT B) OR (NOT A) AND B=A(B′)+(A′)B
We then move to the next highest, the AND, and get:
然后我们转向下一个最高优先级的运算符 AND,得到:
Y = ( A A N D ( N O T B ) ) O R ( ( N O T A ) A N D B ) = ( A ( B ′ ) ) + ( ( A ′ ) B ) Y = (A \ AND \ (NOT \ B)) \ OR \ ((NOT \ A) \ AND \ B) = (A(B')) + ((A')B) Y=(A AND (NOT B)) OR ((NOT A) AND B)=(A(B′))+((A′)B)
And finally, we only have one remaining operator, which we will parenthesize just for completeness to get:
最后,我们只剩下一个运算符,为了完整性,我们将它括号化,得到:
Y = ( ( A A N D ( N O T B ) ) O R ( ( N O T A ) A N D B ) ) = ( ( A B ′ ) ) + ( ( A ′ ) B ) ) Y = ((A \ AND \ (NOT \ B)) \ OR \ ((NOT \ A) \ AND \ B)) = ((AB')) + ((A')B)) Y=((A AND (NOT B)) OR ((NOT A) AND B))=((AB′))+((A′)B))
One of the common mistakes that people make is failing to recognize that, using these very common rules of precedence, that
人们常犯的一个错误是没有认识到,使用这些常见的优先级规则,
A B ′ ≠ ( A B ) ′ AB' \neq (AB)' AB′=(AB)′
Though this WOULD be true if all three operators were deemed to be of the same precedence and to be left associative, which would be unusual but not unheard of.
尽管如果认为所有三个运算符具有相同的优先级并且是左结合的,这将是正确的,这种情况虽然不常见,但并非闻所未闻。
Instead:
相反:
A B ′ = ( A ) ( B ′ ) AB' = (A)(B') AB′=(A)(B′)
Diving Deeper Into Boolean Algebra
深入探索布尔代数
This has been a pretty lightweight article that has hopefully prepared you for a number of articles that will explore many aspects of digital logic and Boolean Algebra at a much deeper level – in fact at a level deeper than most courses go. This is useful because to truly master digital logic design, and it is necessary to be fully conversant with the concepts and subtleties upon which it is based and to also be aware of the common misconceptions and fallacies that frequently trap less well-prepared designers.
这是一篇比较浅显的文章,希望能为你阅读一系列深入探讨数字逻辑和布尔代数许多方面的文章做好准备 —— 事实上,文章的深度超过大多数课程。这是有用的,因为要真正掌握数字逻辑设计,有必要完全熟悉它所基于的概念和细微差别,并且还要了解那些经常使准备不足的设计者陷入困境的常见误解和谬误。
篇外:从布尔代数到 AlexNet——深度学习背后的传承与突破
原标题:这个改变人类命运的软件,终于开源了!
原创 liuxin 码农翻身
2025 年 03 月 31 日 08:55 北京
几乎每一门编程语言,都有一个数据类型叫做 Boolean,它只有两个值:真和假。
这是为了纪念发明布尔代数的数学家乔治・布尔。

乔治・布尔英年早逝,他绝对想不到,他的小女儿艾捷尔・丽莲・伏尼契写了一本著名的小说《牛虻》。
他更不可能想到,他还有一位玄孙:Geoffrey E. Hinton(辛顿),将家族的荣耀推向了巅峰,辛顿不但成了深度学习之父,还获得了图灵奖和诺贝尔奖。

01 算法的积累
辛顿出生于 1947 年,先在剑桥大学获得了实验心理学学士,然后跑到爱丁堡大学拿到了博士学位,他的论文是《放松及其在视觉中的作用》。
这听起来和计算机毫无关系,辛顿为啥会进入到人工智能领域呢?
因为当时的人工智能和计算机科学、心理学和神经科学 “纠缠不清”,每个学科都试图按照自己的领域来描绘技术的前景。
比如早在 1958 年,在海军的资助下,康奈尔大学教授弗兰克・罗森布拉特发明了一个模仿人脑的数学系统:感知机。

感知机有 400 个光传感器,它们一起充当视网膜,将信息传送给大约 1,000 个 “神经元”,这些神经元进行处理并产生单一输出。
用一系列的打孔卡训练以后,感知机居然自己学会了识别卡片上的标记是在左侧还是右侧,这事儿轰动一时,媒体甚至报道 “海军设计了一个会思考的科学怪物”!
我们现在知道,这就是第一个神经网络。
不过,这个神经网络只有一层自适应的权重,想要完成复杂的任务,需要建立一个多层的,每一层都向下一层提供信息,这样就可以学习感知机无法学习的复杂图形。
但是研究人员找不到很好的方法来训练它们,人工智能进入了第一个寒冬。
1978 年,辛顿来到加州大学圣地亚哥分校做博士后研究,在这里他和 David Rumelhart 和 Ronald Williams 合作,重新 “发现” 了用于训练神经网络的反向传播算法,特别是证明了该算法可以使多层神经网络调整自身的权重,从而学习多层特征,完成语言和视觉的任务。
这是一个极其重要的突破,反向传播成为当今深度学习的基础。
1987 年,出于对里根政府的不满,辛顿来到了加拿大,加入了多伦多大学。
虽然辛顿远离了传统的人工智能中心,但是牛人在哪里,哪里就是中心。
辛顿培养了很多著名的学生,其中一位就是来自法国的博士后杨立昆。

杨立昆把反向传播算法应用到了卷积神经网络(CNN)上,他开发的 LeNet 在识别手写数字方面非常出色,在当时的技术条件下就能取得低于 1% 的错误率。
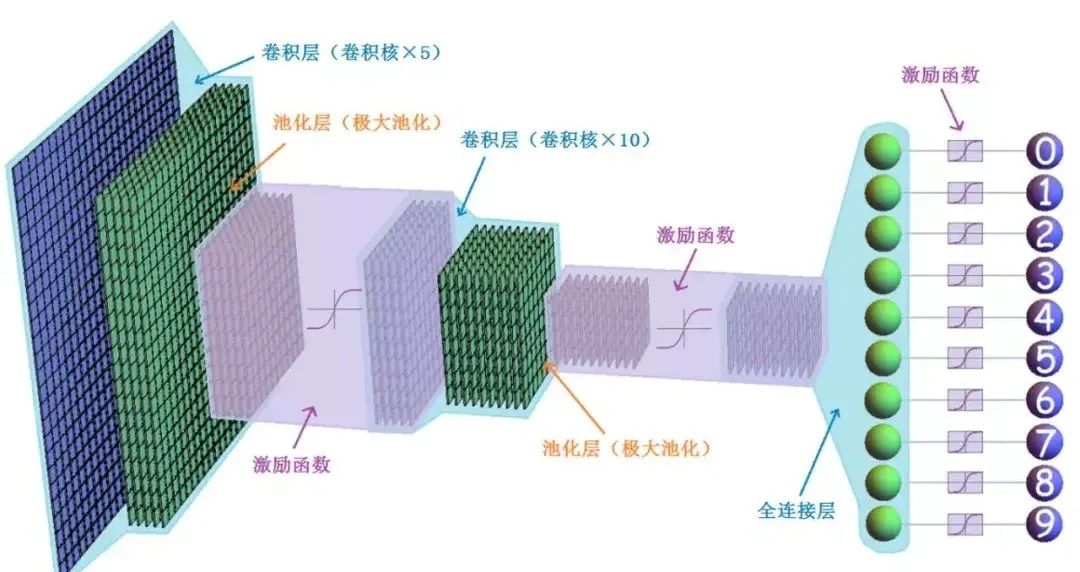

LeNet 后来成功商业化,被金融用来识别支票上的数字。

2019 年,杨立昆和辛顿一起获得了计算机界最高奖:图灵奖。
虽然卷积神经网络在识别数字方面表现优秀,但是在处理图像方面就力不从心了,因为图像识别需要更多、更深的网络隐藏层,当时计算机的计算能力是远远不够的。
神经网络还需要人工智能之外的两项技术来铺平道路:
-
大量的训练数据
-
足够的算力。神经网络训练涉及大量重复的矩阵乘法,最好是并行完成。
02 数据和算力
在过去的 20 年,一切都发生了重大变化。
互联网蓬勃发展,数据变得无处不在,尤其是智能手机的出现,让文本、图像、视频变得唾手可得。
而算力的解决竟然来自于游戏行业,游戏中的图像渲染需要繁重的处理,Nvidia 等公司 开发了图形处理单元 ( GPU) 芯片,游戏开发人员使用 GPU 进行复杂的着色和几何变换。

那些渴望强大计算能力的计算机科学家立刻意识到,他们可以 “欺骗” GPU 执行其他任务,例如训练神经网络。
Nvidia 注意到了这一趋势,它创建了 CUDA,让研究人员可以轻松使用 GPU 进行通用数据处理。
从 2006 年开始,李飞飞计划建立一个图像数据集,涵盖英语中所有名词,用于训练人工智能。

她和她的研究生开始在互联网上收集图像,并使用 WordNet 对它们进行分类。
由于任务极其艰巨,李飞飞和她的合作者最终使用亚马逊的 Mechanical Turk 平台将标记图像的任务众包给了零工。

2009 年 ImageNet 正式完工,比之前的任何图像数据集都大几个数量级。
李飞飞希望它的出现能帮助 AI 实现新的突破,并于 2010 年发起了一场竞赛,激励研究团队改进他们的图像识别算法。
现在我们有了神经网络和算法,训练数据集,以及 GPU 算力,就差一个人把它们都结合起来,震撼世界了。
03 AlexNet
当辛顿的博士生 Ilya Sutskever 看到 ImageNet 时,立刻想起了 Alex Krizhevsky。

(左护法 Illya,右护法 Alex)
Alex 是一位 GPU 编程大师,擅长从一个装有 GPU 的电脑中压榨出最后一点性能。
Ilya 说服 Alex,开始一个新项目,针对 ImageNet 训练一个卷积神经网络,参加 ImageNet 训练。
辛顿也加入了这个项目,担任首席研究员。
Alex 和自己的父母住在一起,他用自己卧室的一台电脑来训练神经网络,电脑上只有两张 Nvidia 显卡。

在一年的时间内,Alex 不断地调整神经网络的参数,重新进行训练,直到 2012 年,这个名叫 AlexNet 的神经网络在竞赛中以 15% 的错误率大幅领先第二名的 26%,以压倒性的优势赢得竞赛,一鸣惊人。
看到 AlexNet 的论文,纽约大学杨立昆实验室的学生们感受到了巨大的失落和遗憾。
因为 AlexNet 使用卷积神经网络,正是杨立昆 80 年代最拿手的工作。
经过 30 年的奋斗,他们跌跌撞撞地走到了最后一关,却眼看着别人破门而入。
杨立昆在当晚讨论 AlexNet 论文的时候,说到:“多伦多大学的学生比纽约大学的学生行动更快。”
当其他资深研究员对 AlexNet 存在怀疑,认为它无法应用到真实世界的数据集上时,杨立昆旗帜鲜明地支持了自己老师的项目:这就是人工智能的转折点!
杨立昆是对的,随后几年的 ImageNet 竞赛中,几乎每个项目都使用了神经网络,到 2017 年许多参赛者的错误率已经降至 5%,主办方随即结束了竞赛。
神经网络在接下来的十年迅速发展,AlphaGo 击败了围棋世界冠军,AI 可以合成逼真的语音,创建图像。
最终,Ilya Sutskever 共同创办的公司 OpenAI 发布了 ChatGPT。
AlexNet 是点燃深度学习的燎原之火,它不但开启了技术革新,还促进了产业重构,甚至引发了社会变革,开启人类深度科技化,说它是改变人类命运的软件是不为过的。
04 结语
百度认识到了 AlexNet 的潜力,微软,Google 也认识到了,电子邮件纷至沓来,他们都力邀辛顿团队加盟,百度甚至为三人开出了 1200 万美元的超高价码。
但是 Ilya 和 Alex 主张成立一个公司,辛顿采纳了学生的意见,创建了 DNNresearch 公司,以对外拍卖的方式来实现价值最大化。
经过激烈的竞争,Google 以 4400 万美元的价格,将这个只有三名员工、没有产品也没有历史的初创公司收入囊中,百度错失了 AI 教父辛顿。
辛顿坚持三人平分这笔钱,但是 Ilya 和 Alex 坚持老师应该拿到更大的份额:40%。辛顿说:“这体现了他们是什么样的人,但没有体现出我是什么样的人。”
2020 年,美国的计算机历史博物馆和 Google 联系,想收录 Alex 这个改变人类世界的软件,经过 5 年的协商,原汁原味的 AlexNet 终于在 GitHub 上开源发布:

纵观 AlexNet 的出现过程,真是一代又一代人的不断努力,不断接力的结果。如果辛顿的团队没做出来,杨立昆的团队,或者别的团队也能完成临门一脚,在当时的条件下,真是万事俱备,只欠东风了。
至于 AlexNet 开启的道路是不是通向通用人工智能之路,我们只有拭目以待了。
via:
-
How Bits and Bytes Work
https://computer.howstuffworks.com/bytes.htm -
How Boolean Logic Works | HowStuffWorks
https://computer.howstuffworks.com/boolean.htm -
Boolean Algebra Basics—An Overview of Boolean Logic
https://www.allaboutcircuits.com/technical-articles/boolean-basics/ -
这个改变人类命运的软件,终于开源了!
https://mp.weixin.qq.com/s/-37YcE_7gxRh9V8fZEOpNw

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








