晶格振动

最新推荐文章于 2022-07-06 11:24:42 发布

东门之杨

最新推荐文章于 2022-07-06 11:24:42 发布

阅读量4.9k

点赞数 4

分类专栏：固体物理文章标签：晶体振动固体物理

本文链接：https://blog.csdn.net/u013795675/article/details/49120333

版权

固体物理专栏收录该内容

8 篇文章 4 订阅

订阅专栏

振动模型

晶体结构中的“格点”是指原子的平衡位置，实际上原子处在不断的振动之中。晶格的振动是典型的小振动问题。

设一定体积内有 $N$ 个质量为 $m$ 的原子，第 $n$ 个原子的平衡位置的位矢为 $\mathbf R_n$ ，偏移量为 $\mu_n(t)$ ，位置矢量为 $\mathbf R_n'=\mathbf R_n+\mu_n(t)$

$N$ 个原子体系的势能在平衡位置的多项式展开为

V = V 0 + \sum i = 1 3 N (\partial V \partial μ i) 0 μ i + 1 2 \sum i = 1 3 N (\partial 2 V \partial μ i μ j) 0 μ i μ j + \dots

$V=V_0+\sum_{i=1}^{3N}\left(\dfrac{\partial V}{\partial \mu_i}\right)_0\mu_i+\dfrac12\sum_{i=1}^{3N}\left(\dfrac{\partial^2 V}{\partial \mu_i\mu_j}\right)_0\mu_i\mu_j+\cdots$

不妨设 $V_0=0$ ；在平衡位置时有 $\dfrac{\partial V}{\partial \mu_i}=0$ ；忽略高于二次的项，得到

V = 1 2 \sum i = 1 3 N (\partial 2 V \partial μ i μ j) 0 μ i μ j

$V=\dfrac12\sum_{i=1}^{3N}\left(\dfrac{\partial^2 V}{\partial \mu_i\mu_j}\right)_0\mu_i\mu_j$
动能的方程

T = 1 2 \sum i = 1 3 N m i μ ˙ 2 i

$T=\dfrac12\sum_{i=1}^{3N}m_i\dot{\mu}_i^2$

由于势能方程中有 $\mu_i\mu_j$ 这样的交叉项，方程很难求解。因此引入简正坐标。

简正坐标

经典力学

根据线性代数的理论，存在这样的正交变换 $\{a_{ij}\}$ 和另一组坐标 $Q_1,Q_2,\dots,Q_{3N}$ ，

m i - - - \sqrt μ i = \sum i = 1 3 N a i j Q j

$\sqrt{m_i}\mu_i=\sum_{i=1}^{3N}a_{ij}Q_j$
使得势能和动能的表达式都称为平方项之和，无交叉项。

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ T = 1 2 \sum 3 N i = 1 Q ˙ 2 i V = 1 2 \sum 3 N i = 1 ω 2 i Q 2 i

$\begin{cases} T=\dfrac12\sum_{i=1}^{3N}\dot{Q}_i^2\\ V=\dfrac12\sum_{i=1}^{3N}\omega_i^2Q_i^2 \end{cases}$

拉格朗日量

L = T - V \Rightarrow p i = \partial L \partial Q ˙ i = Q ˙ i \Rightarrow H = 1 2 \sum i = 1 3 N (p 2 i + ω 2 i Q 2 i)

$L = T-V\\ \Rightarrow p_i=\dfrac{\partial L}{\partial \dot{Q}_i}=\dot{Q}_i\\ \Rightarrow H=\dfrac12\sum_{i=1}^{3N}(p_i^2+\omega_i^2Q_i^2)$

Q ˙ i = \partial H \partial p i = p i \Rightarrow Q ¨ i = p ˙ i

$\dot{Q}_i=\dfrac{\partial H}{\partial p_i}=p_i\\\Rightarrow \ddot{Q}_i=\dot{p}_i$
由应用正则方程得到

Q ¨ i + ω 2 i Q ˙ i = 0

$\ddot{Q}_i+\omega_i^2\dot{Q}_i=0$
这是

3N $3N$ 个独立的简谐振动方程，相应的解为

Q i = A sin (ω i t + δ)

$Q_i=A\sin(\omega_i t+\delta)$
由最初的

μi=1mi−−−√∑3Ni=1aijQj $\mu_i=\dfrac1{\sqrt{m_i}}\sum_{i=1}^{3N}a_{ij}Q_j$ ，知一个简正坐标

Qi $Q_i$ 代表的是体系中所有原子一起的共同振动，称为一个振动模。

量子力学

H = 1 2 \sum i = 1 3 N (p 2 i + ω 2 i Q 2 i)

$H=\dfrac12\sum_{i=1}^{3N}(p_i^2+\omega_i^2Q_i^2)$

⎧ ⎩ ⎨ Q i \to Q i p i \to - i ℏ \partial \partial Q i

$\begin{cases} Q_i\to Q_i\\p_i\to-i\hbar\dfrac{\partial}{\partial Q_i} \end{cases}$
得到系统的薛定谔方程为

\sum i = 1 3 N 1 2 (- ℏ \partial 2 \partial Q 2 i + ω 2 i Q 2 i) Ψ = E Ψ

$\sum_{i=1}^{3N}\dfrac12\left(-\hbar\dfrac{\partial^2}{\partial Q_i^2}+\omega_i^2Q_i^2\right)\Psi=E\Psi$
每个分量满足

1 2 (- ℏ \partial 2 \partial Q 2 i + ω 2 i Q 2 i) Ψ (Q i) = ε i Ψ (Q i)

$\dfrac12\left(-\hbar\dfrac{\partial^2}{\partial Q_i^2}+\omega_i^2Q_i^2\right)\Psi(Q_i)=\varepsilon_i\Psi(Q_i)$
这是典型的谐振子方程，解为

⎧⎩⎨εi=(ni(\?)+12)ℏωiψni(Qi)=|ni⟩

$\begin{cases} \varepsilon_i=(n_i(\?)+\dfrac12)\hbar\omega_i\\ \psi_{n_i}(Q_i)=|n_i\rangle \end{cases}$
系统的能量

E = \sum i = 1 3 N ε i = \sum i = 1 3 N (n i + 1 2) ℏ ω i

$E=\sum_{i=1}^{3N}\varepsilon_i=\sum_{i=1}^{3N}(n_i+\dfrac12)\hbar\omega_i$

一维单原子链

模型

一维晶格，原子间距 $a$ ，质量 $m$ ，每个原子的偏移量 $\mu_{n}$
这里写图片描述

经典力学推导

假设只有邻近原子间存在相互作用，相互作用势只考虑到平方项。
平衡时，两个原子之间的互作用势能为

v (a + δ) = v (a) + d v d r δ + 1 2 d 2 v d r 2 δ 2 + \dots

$v(a+\delta)=v(a)+\dfrac{\mathrm dv}{\mathrm d r}\delta+\dfrac12\dfrac{\mathrm d^2v}{\mathrm dr^2}\delta^2+\cdots$
相互作用力

f = - d v d δ = - d 2 v d r 2 δ = - β δ

$f=-\dfrac{\mathrm dv}{\mathrm d \delta}=-\dfrac{\mathrm d^2v}{\mathrm dr^2}\delta=-\beta\delta$
左右两个原子作用力之和为

- β (μ n - μ n - 1) + β (μ n + 1 - μ n) = β (μ n + 1 + m u n - 1 - 2 μ n)

$-\beta(\mu_n-\mu_{n-1})+\beta(\mu_{n+1}-\mu_n)=\beta(\mu_{n+1}+mu_{n-1}-2\mu_n)$
所以有

m d 2 μ n d t 2 = β (μ n + 1 + μ n - 1 - 2 μ n)

$m\dfrac{\mathrm d^2\mu_n}{\mathrm dt^2}=\beta(\mu_{n+1}+\mu_{n-1}-2\mu_n)$
这是一个线性齐次方程，且一共有N个进行联立，其解的形式是

μ n = A e i (ω t - n a q)

$\mu_n=Ae^{i(\omega t-naq)}$
代回方程可以得到

ω $\omega$ 和

q $q$ 的关系

ω 2 = 2 β m (1 - cos a q)

$\omega^2=\dfrac{2\beta}{m}(1-\cos aq)$

q $q$ 的取值范围

- π a \leq q \leq π a

$-\dfrac \pi a\leq q\leq\dfrac \pi a$
称为 布里渊区。
格波的波长为

λ=2πq $\lambda=\dfrac{2\pi}{q}$

一个格波解代表所有原子做频率相同的振动，相邻原子之间位相差为 $aq$ .

Born-Von Karman条件

μ n + N = μ n \Rightarrow e - i N a q = 1 \Rightarrow q = 2 π N a \cdot h

$\mu_{n+N}=\mu_n\\\Rightarrow e^{-iNaq}=1\\\Rightarrow q=\dfrac{2\pi}{Na}\cdot h$
即

q $q$ 的取值范围是

−πa $-\dfrac\pi a$ 到

πa $\dfrac\pi a$ 之间的N个不同数值.

色散关系

ω = 2 β m (1 - cos a q) - - - - - - - - - - - - \sqrt = 2 β m - - - \sqrt ∣ ∣ ∣ sin 1 2 a q ∣ ∣ ∣

$\omega=\sqrt{\dfrac{2\beta}{m}(1-\cos aq)}=2\sqrt{\dfrac{\beta}{m}}\left|\sin\dfrac12 aq\right|$
长波极限，当

|aq|→0 $|aq|\to0$ 时，

ω∼|q|,λ $\omega\sim|q|,\lambda$ 很大，相邻原子的相位差

aq $aq$ 很小，一个波长内包含很多原子，晶格近乎连续

ω−q $\omega-q$ 图接近连续
短波极限，当

|aq|→π $|aq|\to\pi$ 时，一个波长内仅包含两个原子。相邻两个原子相位相差

π $\pi$ .

声子

结合一维单原子链模型和简正坐标，可以知道第 $q$ 个格波引起的第 $n$ 个原子的位移

μ n q = A q e i (ω q t - n a q)

$\mu_{nq}=A_qe^{i(\omega_qt-naq)}$
第

n $n$ 个原子的总位移

μ n = \sum q μ n q = \sum q A q e i (ω q t - n a q)

$\mu_n=\sum_q\mu_{nq}=\sum_qA_qe^{i(\omega_qt-naq)}$
引入简正坐标，

Q q = N m - - - - \sqrt A e i ω q t

$Q_q=\sqrt{Nm}Ae^{i\omega_q t}$
则

μ n = 1 N m - - - - \sqrt \sum q Q q e - i n a q

$\mu_n=\dfrac1{\sqrt{Nm}}\sum_qQ_qe^{-inaq}$
对比一下引入简正坐标时

m i - - - \sqrt μ i = \sum i = 1 3 N a i j Q j

$\sqrt{m_i}\mu_i=\sum_{i=1}^{3N}a_{ij}Q_j$
得

a n q = 1 N - - \sqrt e - i n a q

$a_{nq}=\dfrac1{\sqrt{N}}e^{-inaq}$

在引入简正坐标之后，可以将总动能和势能表示为

T = 1 2 \sum q | Q ˙ q | 2 U = 1 2 \sum q ω 2 q | Q 2 q |

$T=\dfrac12\sum_q|\dot{Q}_q|^2\\U=\dfrac12\sum_q\omega_q^2|Q_q^2|$
哈密顿量

H = T + U = 1 2 \sum q (| Q ˙ q | 2 + ω 2 q | Q 2 q |)

$H=T+U=\dfrac12\sum_q\left(|\dot{Q}_q|^2+\omega_q^2|Q_q^2|\right)$

利用简正坐标推导，结论可以直接过渡到量子理论。对任一简正坐标 $q$ ，

1 2 ⎛ ⎝ - ℏ \partial 2 \partial Q 2 q + ω 2 q Q 2 q ⎞ ⎠ ψ (Q q) = ε q ψ (Q q)

$\dfrac12\left(-\hbar\dfrac{\partial^2}{\partial Q_q^2}+\omega_q^2Q_q^2\right)\psi(Q_q)=\varepsilon_q\psi(Q_q)$

ε q = (n q + 1 2) ℏ ω q

$\varepsilon_q=(n_q+\dfrac12)\hbar\omega_q$

波数为 $q$ 的格波的量子，称为声子。
当振动模式处于 $(n_q+\dfrac12)\hbar\omega_q$ 的时候，就说有 $n_q$ 个声子。
声子可以与电子、光子发生相互作用，交换能量。
声子是一种准粒子，具有动量和能量。
格波在晶体中可以理解成声子和原子的碰撞。
电子波在晶体中的散射可以理解成声子和电子的相互作用。
光在晶体中的散射可以看作是光子和声子之间的相互作用。

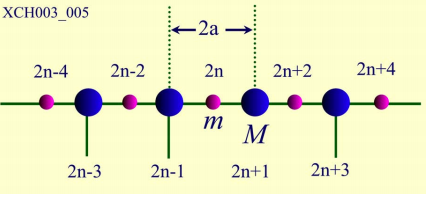
一维双原子链

最简单的复式晶格。

模型

原胞 $a,M,m$ ，晶格常数 $2a$
这里写图片描述

牛顿力学推导

m d 2 μ 2 n d t 2 = β (μ 2 n + 1 + μ 2 n - 1 - 2 μ 2 n) M d 2 μ 2 n + 1 d t 2 = β (μ 2 n + 2 + μ 2 n - 2 μ 2 n + 1)

$m\dfrac{\mathrm d^2\mu_{2n}}{\mathrm dt^2}=\beta(\mu_{2n+1}+\mu_{2n-1}-2\mu_{2n})\\ M\dfrac{\mathrm d^2\mu_{2n+1}}{\mathrm dt^2}=\beta(\mu_{2n+2}+\mu_{2n}-2\mu_{2n+1})$
体系有

2N $2N$ 个独立的方程。格波解的形式仍为

μ 2 n = A e i (ω t - 2 n a q) μ 2 n + 1 = B e i (ω t - (2 n + 1) a q)

$\mu_{2n}=Ae^{i(\omega t-2naq)}\\ \mu_{2n+1}=Be^{i(\omega t-(2n+1)aq)}$

A,B $A,B$ 分别为两种原子的振幅，因为质量一般不同，所以两个振幅一般也不同。

代回方程得到 $\omega$ 和 $q$ 的关系

{- m ω 2 A = β (e i a q + e - i a q) B - 2 β A - M ω 2 B = β (e i a q + e - i a q) A - 2 β B

$\begin{cases} -m\omega^2A=\beta(e^{iaq}+e^{-iaq})B-2\beta A\\ -M\omega^2B=\beta(e^{iaq}+e^{-iaq})A-2\beta B \end{cases}$
整理得

{A (m ω 2 - 2 β) + B \cdot 2 β cos a q = 0 A \cdot 2 β cos a q + B (M ω 2 - 2 β) = 0

$\begin{cases} A(m\omega^2-2\beta) +B\cdot2\beta \cos aq=0\\ A\cdot2\beta\cos aq +B(M\omega^2-2\beta)=0 \end{cases}$

A,B $A,B$ 有解的条件是

∣ ∣ ∣ m ω 2 - 2 β 2 β cos a q 2 β cos a q M ω 2 - 2 β ∣ ∣ ∣

$\begin{vmatrix} m\omega^2-2\beta & 2\beta \cos aq\\ 2\beta\cos aq & M\omega^2-2\beta \end{vmatrix}$
为

0 $0$ .
由此得到

w−q $w-q$ 关系

m M ω 4 - 2 β (m + M) ω 2 + 4 β 2 sin 2 a q = 0

$mM\omega^4-2\beta(m+M)\omega^2+4\beta^2\sin ^2aq=0$
解得

ω 2 = β m M [(m + M) \pm (m - M) 2 + 4 m N cos 2 a q - - - - - - - - - - - - - - - - - - - - \sqrt]

$\omega^2=\dfrac{\beta}{mM}\left[(m+M)\pm\sqrt{(m-M)^2+4mN\cos^2aq}\right]$
从而得到

ω $\omega$ 的两个不同的解

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ω 2 + = β m M [(m + M) + (m - M) 2 + 4 m N cos 2 a q - - - - - - - - - - - - - - - - - - - - \sqrt] ω 2 - = β m M [(m + M) - (m - M) 2 + 4 m N cos 2 a q - - - - - - - - - - - - - - - - - - - - \sqrt]

$\begin{cases} \omega^2_+=\dfrac{\beta}{mM}\left[(m+M)+\sqrt{(m-M)^2+4mN\cos^2aq}\right]\\ \omega^2_-=\dfrac{\beta}{mM}\left[(m+M)-\sqrt{(m-M)^2+4mN\cos^2aq}\right] \end{cases}$

q $q$ 的取值范围

- π 2 a \leq q \leq π 2 a

$-\dfrac \pi {2a}\leq q\leq\dfrac \pi {2a}$
为 布里渊区。

一个格波解代表所有原子做频率相同的振动，相邻原子之间位相差为 $aq$ ，相邻两个原胞之间的相位差为 $2aq$ .

将 $\omega_+^2$ 和 $\omega_-^2$ 分别代入

{A (m ω 2 - 2 β) + B \cdot 2 β cos a q = 0 A \cdot 2 β cos a q + B (M ω 2 - 2 β) = 0

$\begin{cases} A(m\omega^2-2\beta) +B\cdot2\beta \cos aq=0\\ A\cdot2\beta\cos aq +B(M\omega^2-2\beta)=0 \end{cases}$
得到

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ (B A) + = - m ω 2 + - 2 β 2 β cos a q (B A) - = - m ω 2 - - 2 β 2 β cos a q

$\begin{cases} \left(\dfrac BA\right)_+=-\dfrac{m\omega_+^2-2\beta}{2\beta\cos aq}\\ \left(\dfrac BA\right)_-=-\dfrac{m\omega_-^2-2\beta}{2\beta\cos aq} \end{cases}$

Born-Von Karman条件

μ n + N = μ n \Rightarrow e - i \cdot 2 N a q = 1 \Rightarrow q = π N a \cdot h

$\mu_{n+N}=\mu_n\\\Rightarrow e^{-i\cdot2Naq}=1\\\Rightarrow q=\dfrac{\pi}{Na}\cdot h$
即

q $q$ 的取值范围是

−πa $-\dfrac\pi a$ 到

πa $\dfrac\pi a$ 之间的N个不同数值，因为每一个

q $q$ 对应两个

ω $\omega$ 的值，所以共有

2N $2N$ 个振动模。

声学波和光学波

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ω 2 + = β m M [(m + M) + (m - M) 2 + 4 m N cos 2 a q - - - - - - - - - - - - - - - - - - - - \sqrt] ω 2 - = β m M [(m + M) - (m - M) 2 + 4 m N cos 2 a q - - - - - - - - - - - - - - - - - - - - \sqrt]

$\begin{cases} \omega^2_+=\dfrac{\beta}{mM}\left[(m+M)+\sqrt{(m-M)^2+4mN\cos^2aq}\right]\\ \omega^2_-=\dfrac{\beta}{mM}\left[(m+M)-\sqrt{(m-M)^2+4mN\cos^2aq}\right] \end{cases}$

ω+ $\omega_+$ 称为 光学波，

ω− $\omega_-$ 称为 声学波。

长波极限，当 $|aq|\to0$ 时，

⎧ ⎩ ⎨ ω + = 2 β ( m + M ) m M - - - - - - - - - - \sqrt ω - = 0

$\begin{cases} \omega_+=\sqrt{\dfrac{2\beta(m+M)}{mM}}\\ \omega_-=0 \end{cases}$
相邻原子的相位差

aq $aq$ 很小，一个波长内包含很多原子，晶格近乎连续

ω−q $\omega-q$ 图接近连续

短波极限，当 $|aq|\to\dfrac\pi2$ 时，

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ω + = 2 β m - - - \sqrt (假 设 m < M) ω - = 2 β M - - - \sqrt

$\begin{cases} \omega_+=\sqrt{\dfrac{2\beta}{m}}\quad(假设m<M)\\ \omega_-=\sqrt{\dfrac{2\beta}{M}} \end{cases}$

可见 $(\omega_+)_{\min}>(\omega_-)_{\max}$ ，因此在 $(\omega_+)_{\min}$ 和 $(\omega_-)_{\max}$ 之间不存在振动模。

色散关系

两种原子的振幅比

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ (B A) + = - m ω 2 + - 2 β 2 β cos a q (B A) - = - m ω 2 - - 2 β 2 β cos a q

$\begin{cases} \left(\dfrac BA\right)_+=-\dfrac{m\omega_+^2-2\beta}{2\beta\cos aq}\\ \left(\dfrac BA\right)_-=-\dfrac{m\omega_-^2-2\beta}{2\beta\cos aq} \end{cases}$

当 $q\to\pm\dfrac{\pi}{2a}$ 时，声学波

(B A) - = - m ω 2 - - 2 β 2 β cos a q \to \infty

$\left(\dfrac BA\right)_-=-\dfrac{m\omega_-^2-2\beta}{2\beta\cos aq}\to\infty$
即

B≫A $B\gg A$ ，此时可以认为

A≈0 $A\approx0$ ，

三维晶格的振动

运动方程

色散关系

波矢取值

晶格振动谱

布里渊区

东门之杨

关注

4
点赞
踩
16

收藏

觉得还不错? 一键收藏
1
评论
晶格振动

振动模型晶体结构中的“格点”是指原子的平衡位置，实际上原子处在不断的振动之中。晶格的振动是典型的小振动问题。设一定体积内有NN个质量为mm的原子，第nn个原子的平衡位置的位矢为Rn\mathbf R_n，偏移量为μn(t)\mu_n(t)，位置矢量为R′n=Rn+μn(t)\mathbf R_n'=\mathbf R_n+\mu_n(t)NN个原子体系的势能在平衡位置的多项式展开为 V=V0+∑i
复制链接

扫一扫